Implicit Differentiation is another chain rule Implicit Differentiation


![If h(x) = [g(x)]n then h’(x) = n [g(x)]n-1 g’(x) We review the power If h(x) = [g(x)]n then h’(x) = n [g(x)]n-1 g’(x) We review the power](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-3.jpg)
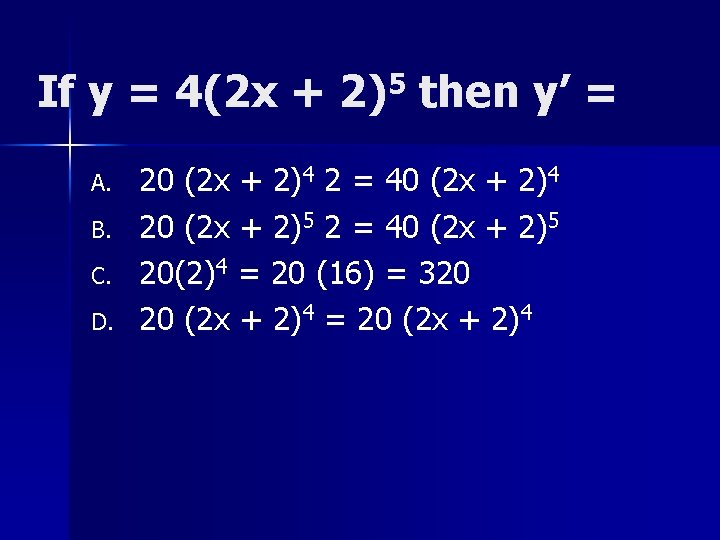
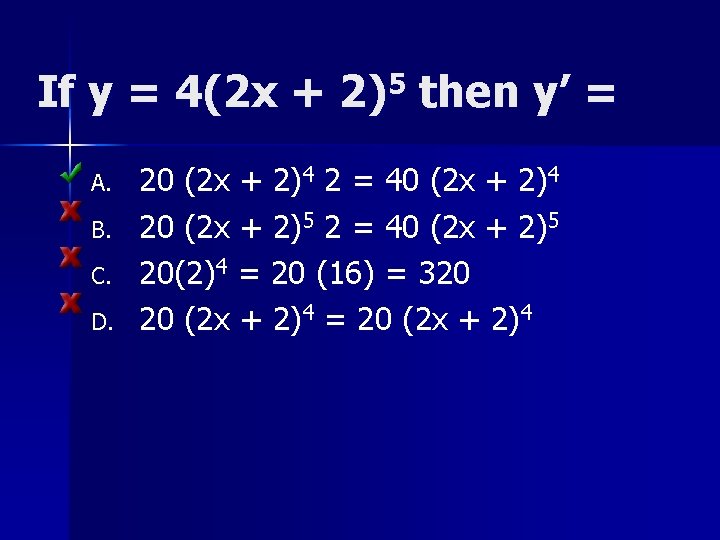
![If h(x) = [3 x + cos(x)]7 h’(x) = A. B. C. D. 21 If h(x) = [3 x + cos(x)]7 h’(x) = A. B. C. D. 21](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-6.jpg)
![If h(x) = [3 x + cos(x)]7 h’(x) = A. B. C. D. 21 If h(x) = [3 x + cos(x)]7 h’(x) = A. B. C. D. 21](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-7.jpg)
![Replace g(x) with y. Instead of ([g(x)]n )’ = n [g(x)]n-1 g’(x) We get Replace g(x) with y. Instead of ([g(x)]n )’ = n [g(x)]n-1 g’(x) We get](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-8.jpg)
![Replace g(x) with y. We get (y n )’ = n [ y ]n-1 Replace g(x) with y. We get (y n )’ = n [ y ]n-1](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-9.jpg)




![2 [(x+1)(x -3)]’ Recall = (x+1)(2 x)+ (x 2 -3) So [(x+1)y]’ = (x+1)y’ 2 [(x+1)(x -3)]’ Recall = (x+1)(2 x)+ (x 2 -3) So [(x+1)y]’ = (x+1)y’](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-14.jpg)
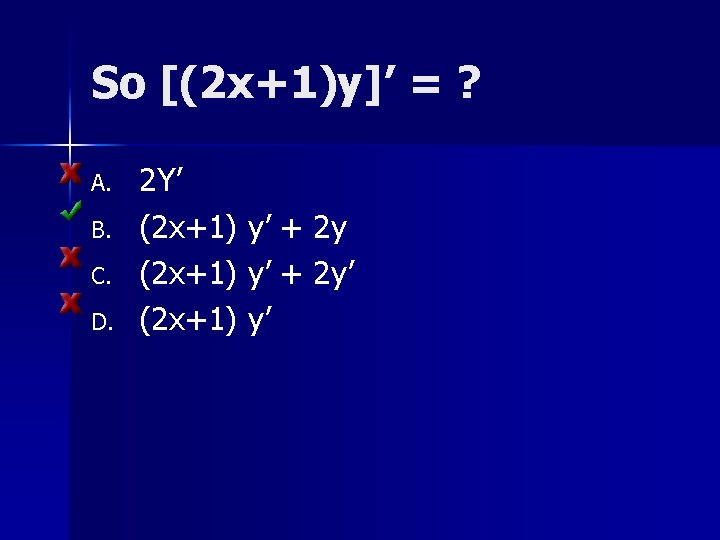
![Find [2 y 6 + tan(2 x)]’ A. B. C. D. 12 y 5 Find [2 y 6 + tan(2 x)]’ A. B. C. D. 12 y 5](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-16.jpg)

















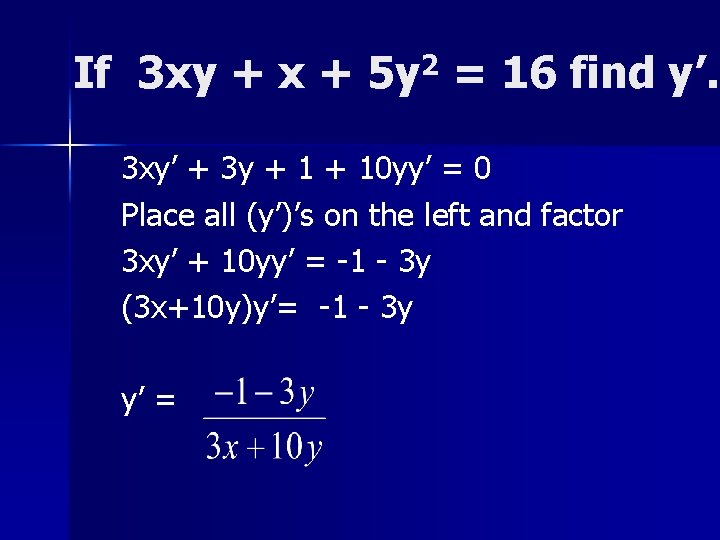

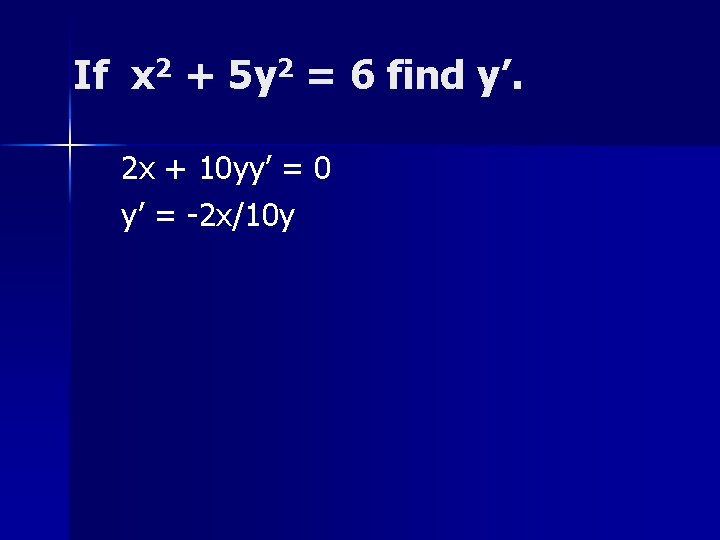
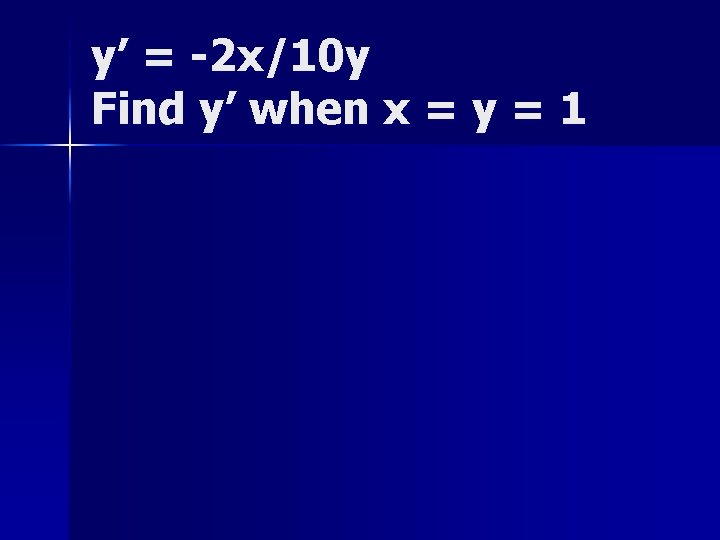
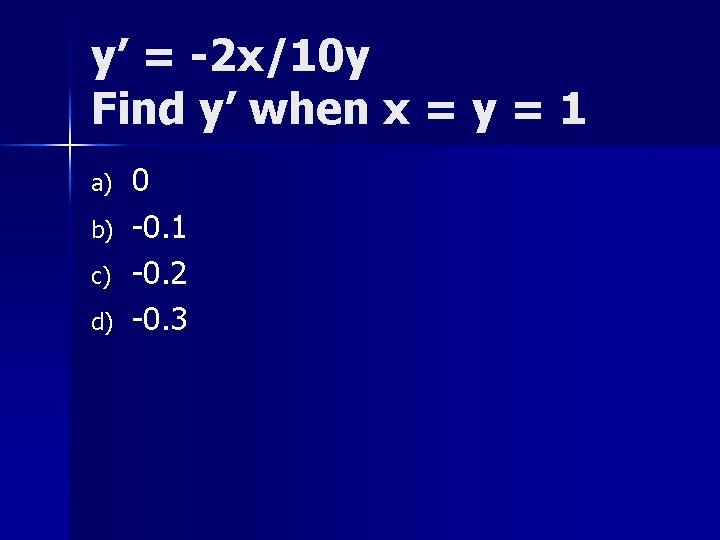
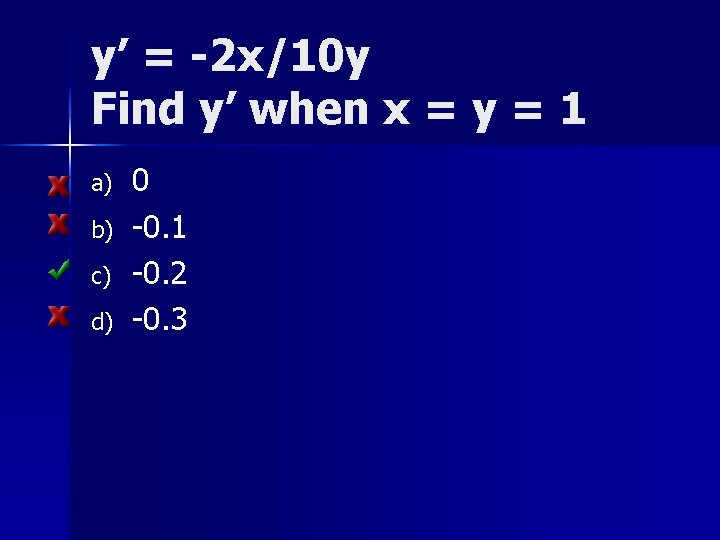
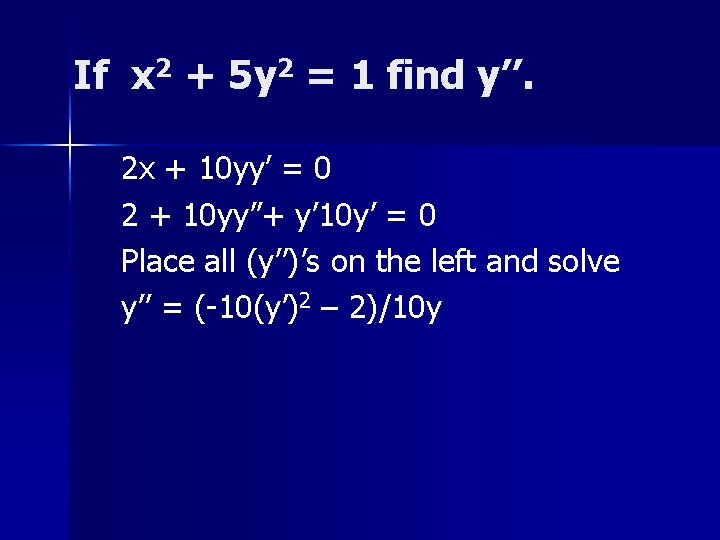
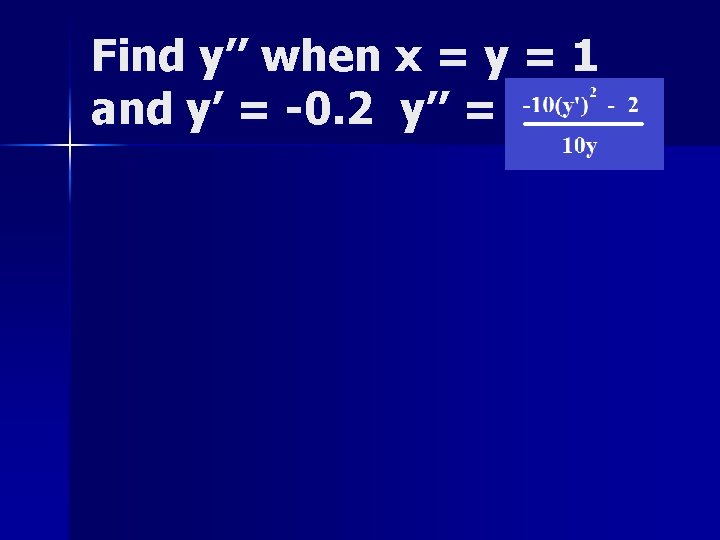
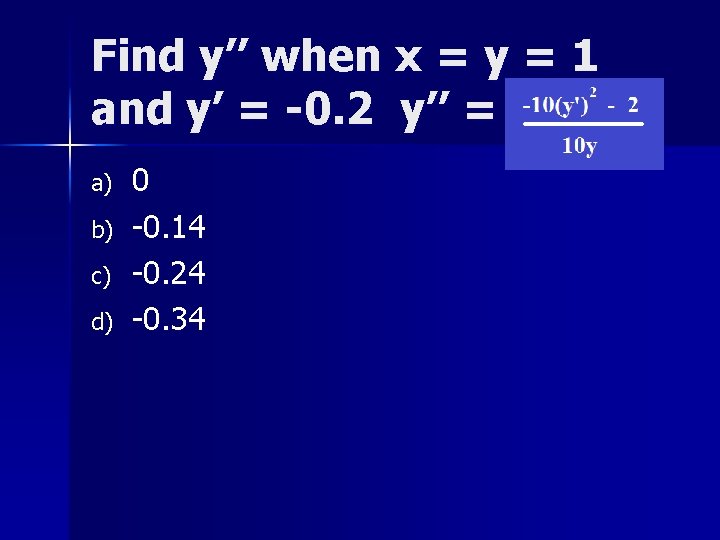
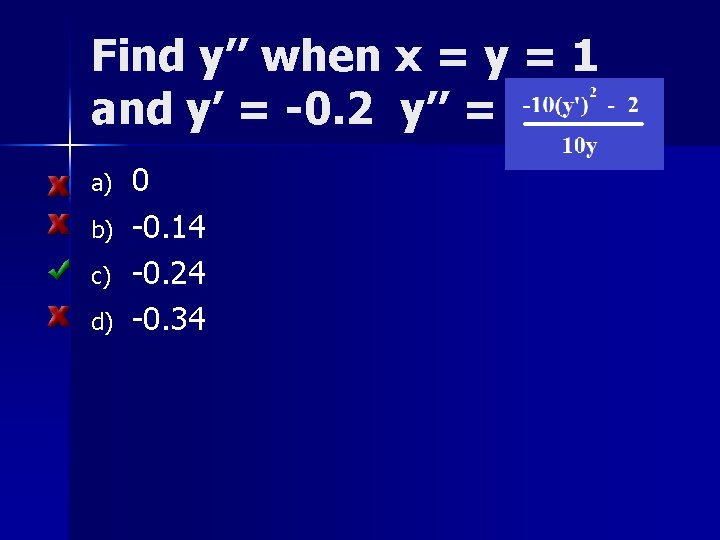




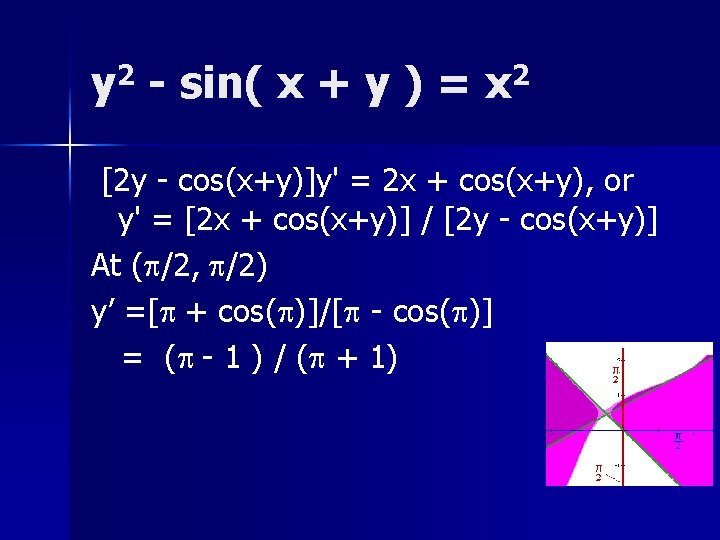
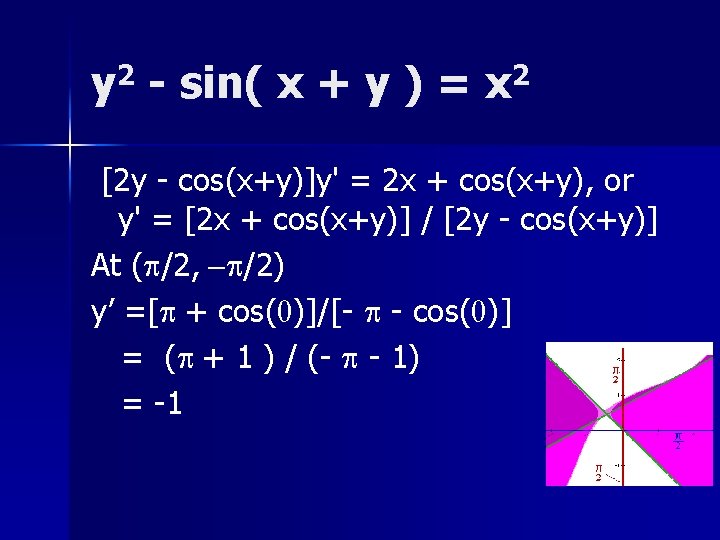
![y’=[2 x+cos(x+y)] / [2 y-cos(x+y)] Find y’ at (-p/2, -p/2) to one decimal. 1. y’=[2 x+cos(x+y)] / [2 y-cos(x+y)] Find y’ at (-p/2, -p/2) to one decimal. 1.](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-53.jpg)



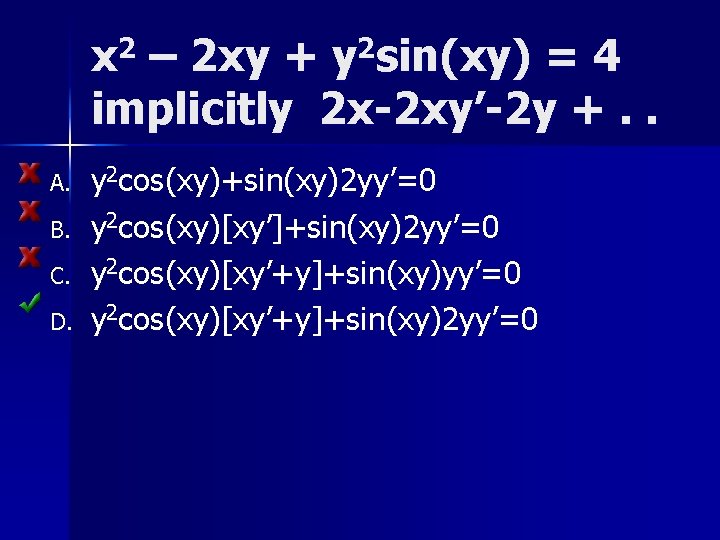

![2 x -2 xy’ 2 y+y 2 cos(xy)[xy’+y]+2 sin(xy)yy’=0 Find y’ at (-2, 0) 2 x -2 xy’ 2 y+y 2 cos(xy)[xy’+y]+2 sin(xy)yy’=0 Find y’ at (-2, 0)](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-59.jpg)
![Theorem – If n is an integer, [xn]’ =nxn-1 Use mathematical induction for positive Theorem – If n is an integer, [xn]’ =nxn-1 Use mathematical induction for positive](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-60.jpg)
![Theorem – If q is rational, [xq]’ =qxq-1 Since q is rational, there exist Theorem – If q is rational, [xq]’ =qxq-1 Since q is rational, there exist](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-61.jpg)











































- Slides: 106

Implicit Differentiation is another chain rule.

Implicit Differentiation is another chain rule. Nothing new today except we don’t know what y is.
![If hx gxn then hx n gxn1 gx We review the power If h(x) = [g(x)]n then h’(x) = n [g(x)]n-1 g’(x) We review the power](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-3.jpg)
If h(x) = [g(x)]n then h’(x) = n [g(x)]n-1 g’(x) We review the power rule.
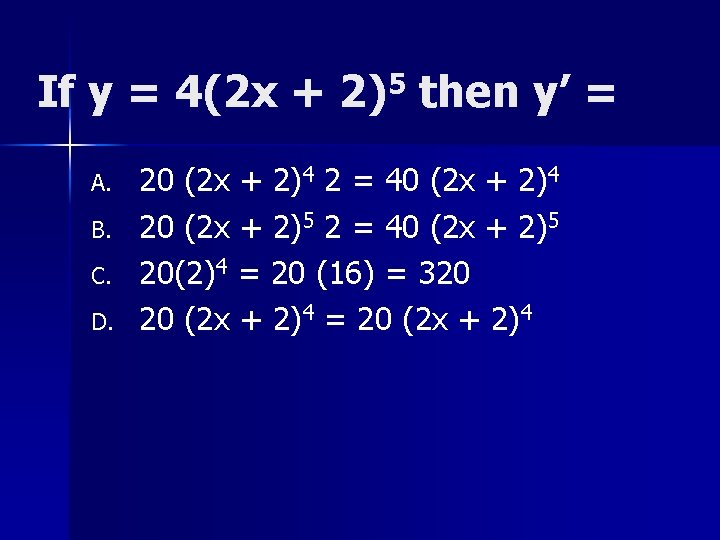
If y = 4(2 x + 2)5 then y’ = A. B. C. D. 20 (2 x + 2)4 2 = 40 (2 x + 2)4 20 (2 x + 2)5 2 = 40 (2 x + 2)5 20(2)4 = 20 (16) = 320 20 (2 x + 2)4 = 20 (2 x + 2)4
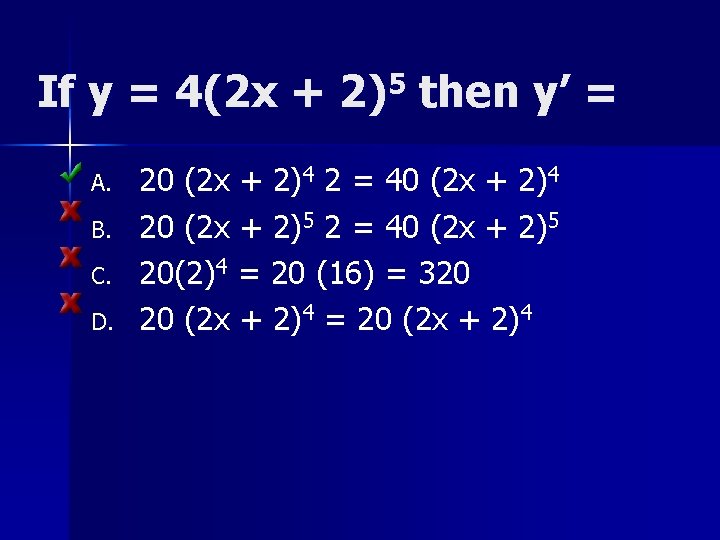
If y = 4(2 x + 2)5 then y’ = A. B. C. D. 20 (2 x + 2)4 2 = 40 (2 x + 2)4 20 (2 x + 2)5 2 = 40 (2 x + 2)5 20(2)4 = 20 (16) = 320 20 (2 x + 2)4 = 20 (2 x + 2)4
![If hx 3 x cosx7 hx A B C D 21 If h(x) = [3 x + cos(x)]7 h’(x) = A. B. C. D. 21](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-6.jpg)
If h(x) = [3 x + cos(x)]7 h’(x) = A. B. C. D. 21 x + 7 cos(x) 7 [3 x + cos(x)] 6[3 + sin(x)] 7 [3 x + cos(x)] 6[3 - sin(x)] 7 [3 - sin(x)]6
![If hx 3 x cosx7 hx A B C D 21 If h(x) = [3 x + cos(x)]7 h’(x) = A. B. C. D. 21](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-7.jpg)
If h(x) = [3 x + cos(x)]7 h’(x) = A. B. C. D. 21 x + 7 cos(x) 7 [3 x + cos(x)] 6[3 + sin(x)] 7 [3 x + cos(x)] 6[3 - sin(x)] 7 [3 - sin(x)]6
![Replace gx with y Instead of gxn n gxn1 gx We get Replace g(x) with y. Instead of ([g(x)]n )’ = n [g(x)]n-1 g’(x) We get](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-8.jpg)
Replace g(x) with y. Instead of ([g(x)]n )’ = n [g(x)]n-1 g’(x) We get (y n )’ = n [ y ]n-1 y’
![Replace gx with y We get y n n y n1 Replace g(x) with y. We get (y n )’ = n [ y ]n-1](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-9.jpg)
Replace g(x) with y. We get (y n )’ = n [ y ]n-1 y’

Guidelines for Finding the Derivative Implicitly Let y stand for one of any number of functions. In this case, 4 different functions.

Number of heart beats per minute, t seconds after the beginning of a race is given by Find R’(t) =

Number of heart beats per minute, t seconds after the beginning of a race is given by Find R’(t)

Number of heart beats per minute, t seconds after the beginning of a race is given by Find R’(t).
![2 x1x 3 Recall x12 x x 2 3 So x1y x1y 2 [(x+1)(x -3)]’ Recall = (x+1)(2 x)+ (x 2 -3) So [(x+1)y]’ = (x+1)y’](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-14.jpg)
2 [(x+1)(x -3)]’ Recall = (x+1)(2 x)+ (x 2 -3) So [(x+1)y]’ = (x+1)y’ + y [3 y 3 ]’ = 9 y 2 y’
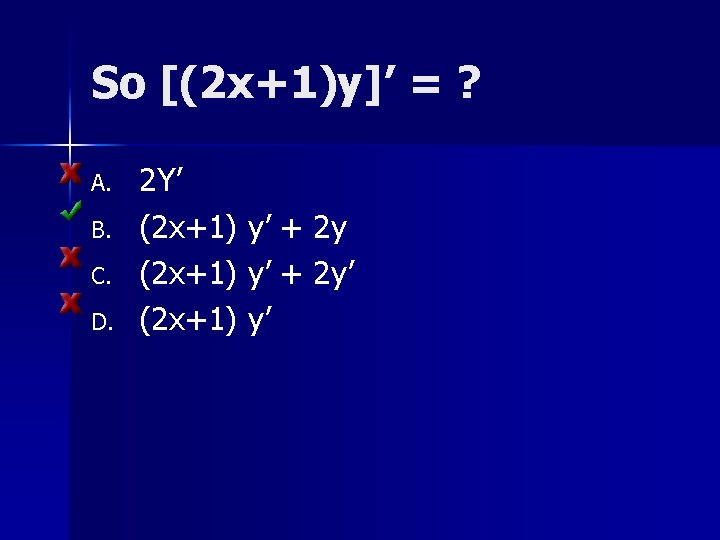
![Find 2 y 6 tan2 x A B C D 12 y 5 Find [2 y 6 + tan(2 x)]’ A. B. C. D. 12 y 5](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-16.jpg)
Find [2 y 6 + tan(2 x)]’ A. B. C. D. 12 y 5 y’ – sec 2(2 x) 2 12 y 5 y’ + csc 2(2 x) 2 12 y 5 + sec 2(2 x) 2

Guidelines for Finding the Derivative Implicitly Let y stand for one of any number of functions. Differentiate both sides of the equation, using chain rule, power rule, product rule quotient rule.

If 2 x + 2 y = 36 find y’. What is the derivative of x 2 ? 2 x What is the derivative of y 2 ? 2 yy’ What is the derivative of 36 ?

What is the derivative of 36? A. B. C. 36 x 36 0

What is the derivative of 36? A. B. C. 36 x 36 0

Differentiate both sides 2 2 x + y = 36 A. B. C. 2 x + 2 yy’ = 0 2 x + 2 yy’ = 36 2 x + 2 y = 0

Differentiate both sides 2 2 x + y = 36 A. B. C. 2 x + 2 yy’ = 0 2 x + 2 yy’ = 36 2 x + 2 y = 0

If 2 x + 2 y 2 x + 2 yy’ = 0 2 yy’ = -2 x = 36 find y’.

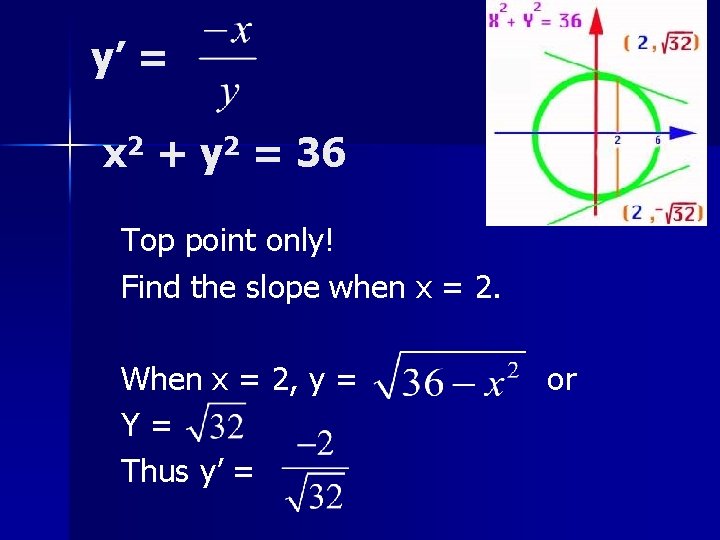
If x 2 + y 2 = 36 find y’. 2 yy’ = -2 x yy’ = -x y’ =

y’ = x 2 + y 2 = 36 Top point only! Find the slope when x = 2. When x = 2, y = Y= Thus y’ = or

y’ = Y’ = for top point bottom point

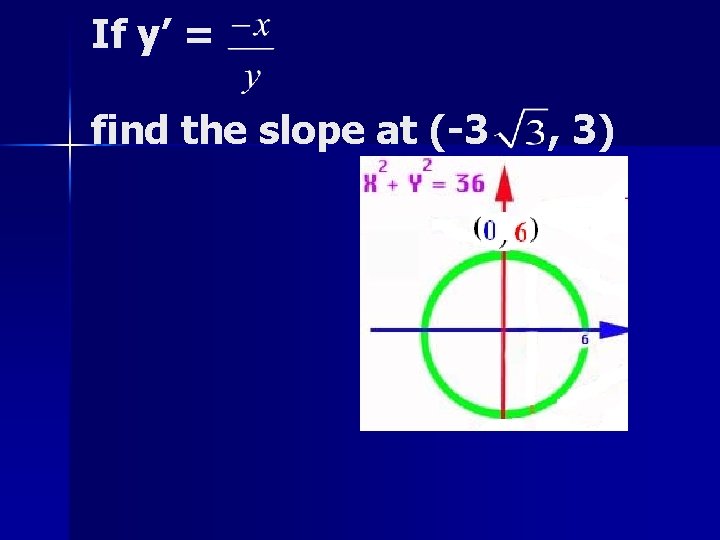
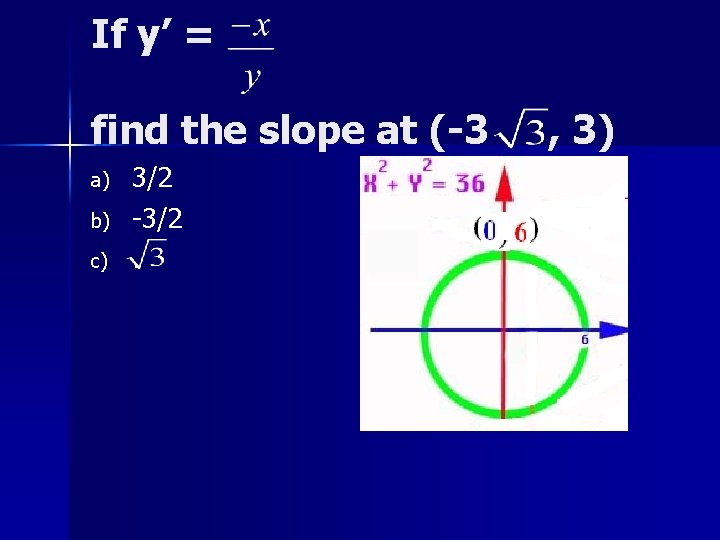
If y’ = find the slope at (-3 , 3)

If y’ = find the slope at (-3 a) b) c) 3/2 -3/2. , 3)

If y’ = find the slope at (-3 a) b) c) 3/2 -3/2 + , 3)

Thus if the dolphins forehead could be approximated by a circle, we could calculate the slope there if we knew the x and y coordinates. y’ =

And if the dolphins throat could be approximated by a circle, we could calculate the slope there if we knew the x and y coordinates. y’ =

Let Y stand for one of 5 functions. If 3 x 2 + xy 5 = 16 x find y’. What is the derivative of 3 x 2 ? 6 x What is the derivative of xy 5 ? x 5 y 4 y’+y 5 What is the derivative of 16 x ?

Differentiate xy 5 using the product rule and power rule x 5 y 4 y’ + y 5

3 x 2 + xy 5 = 16 x Differentiate both sides A. B. C. D. 6 x + 5 y 4 y’= 16 6 x +5 xy 4 y’+y 5 = 16 6 + 6 x +5 xy 4 y’+y 5 = 0

3 x 2 + xy 5 = 16 x Differentiate both sides A. B. C. D. 6 x + 5 y 4 y’= 16 6 x +5 xy 4 y’+y 5 = 16 6 + 6 x +5 xy 4 y’+y 5 = 0

Guidelines for Finding the Derivative Implicitly Let y stand for one of 5 functions. Differentiate both sides of the equation, using chain rule, power rule, product rule, quotient rule.
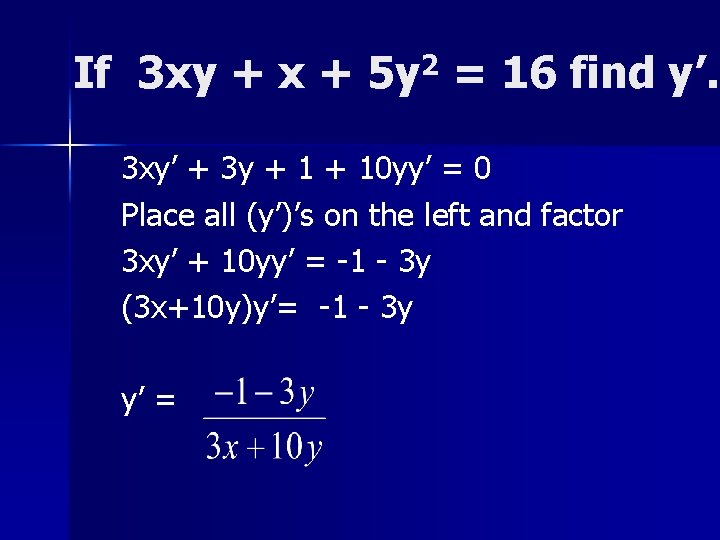
If 3 xy + x + 2 5 y = 16 find y’. 3 xy’ + 3 y + 10 yy’ = 0 Place all (y’)’s on the left and factor 3 xy’ + 10 yy’ = -1 - 3 y (3 x+10 y)y’= -1 - 3 y y’ =

If 3 xy + x + 5 y 2 = 16 find y’’. 3 xy’ + 3 y + 10 yy’ = 0 3 xy’’ + 3 y’ + 10 yy’’ + 10(y’)2 = 0 Place all (y’’)’s on the left and factor (3 x+10 y)y’’= -6 y’ - 10(y’)2
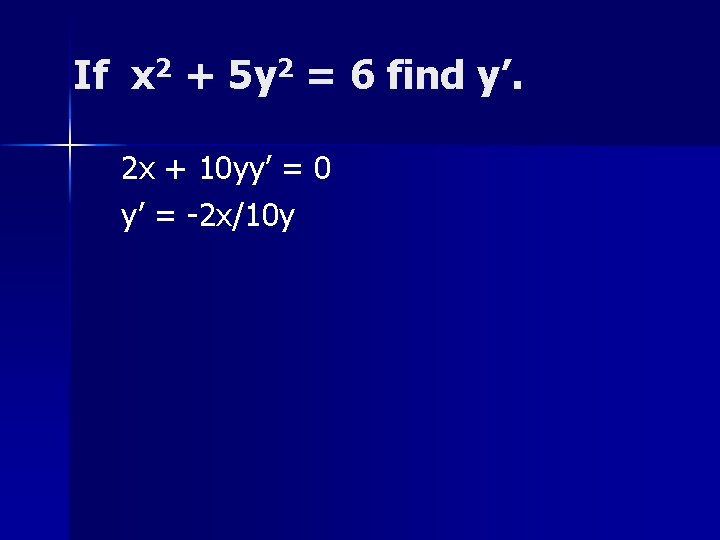
If x 2 + 5 y 2 = 6 find y’. 2 x + 10 yy’ = 0 y’ = -2 x/10 y
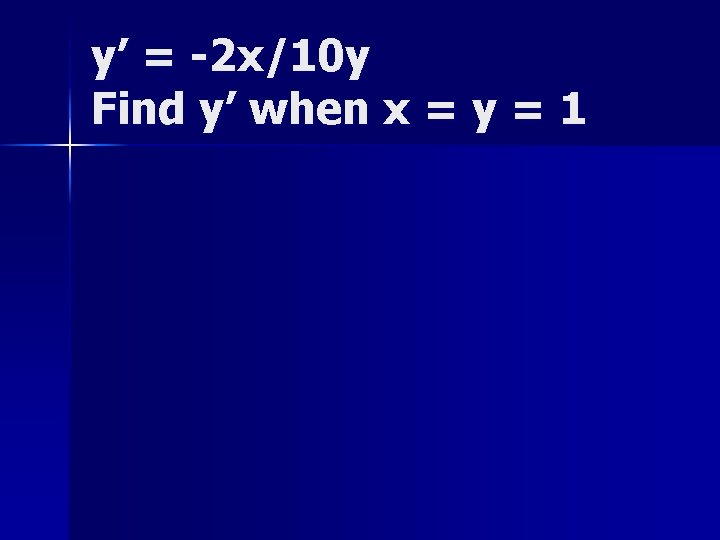
y’ = -2 x/10 y Find y’ when x = y = 1
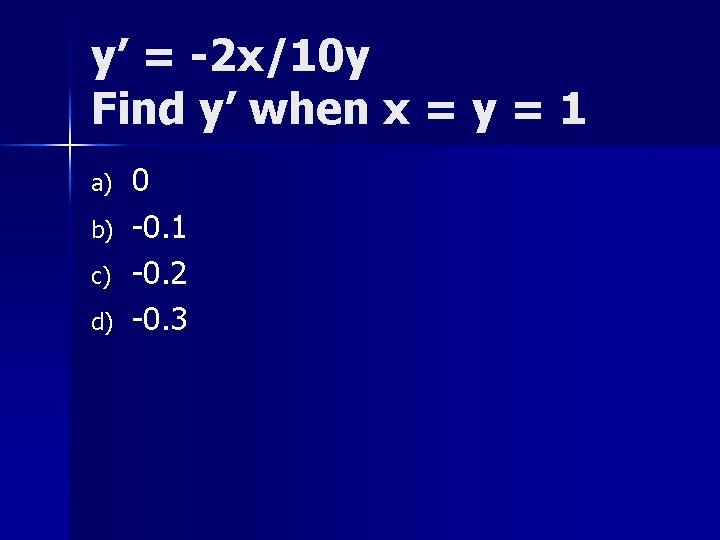
y’ = -2 x/10 y Find y’ when x = y = 1 a) b) c) d) 0 -0. 1 -0. 2 -0. 3
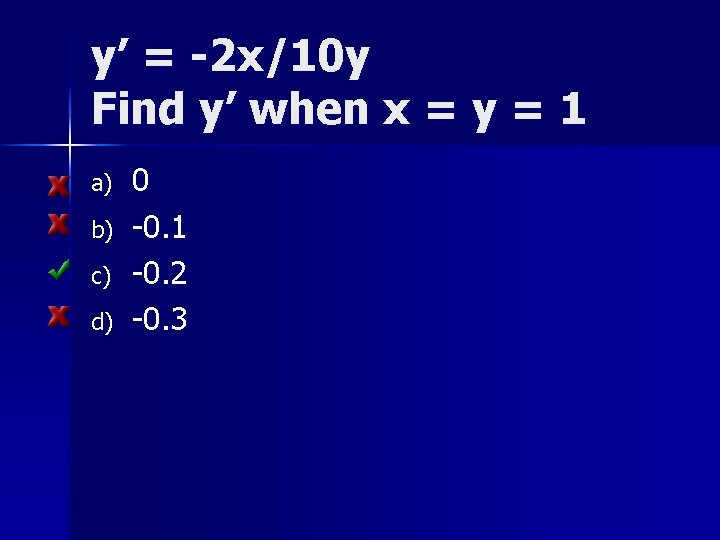
y’ = -2 x/10 y Find y’ when x = y = 1 a) b) c) d) 0 -0. 1 -0. 2 -0. 3
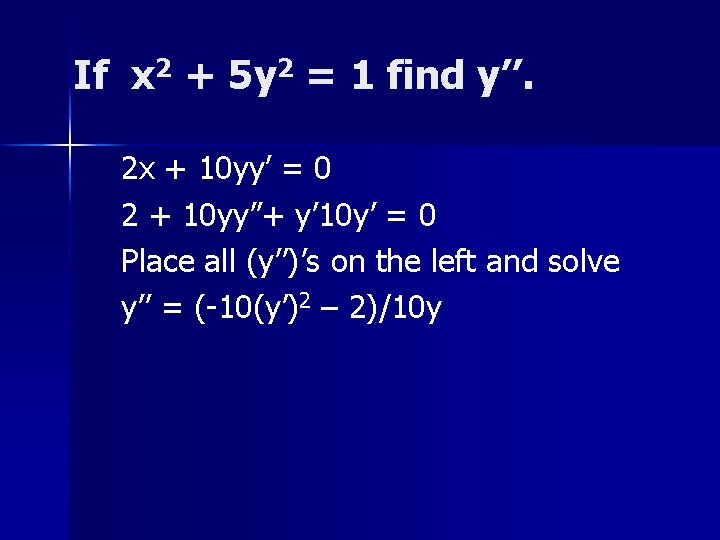
If x 2 + 5 y 2 = 1 find y’’. 2 x + 10 yy’ = 0 2 + 10 yy’’+ y’ 10 y’ = 0 Place all (y’’)’s on the left and solve y’’ = (-10(y’)2 – 2)/10 y
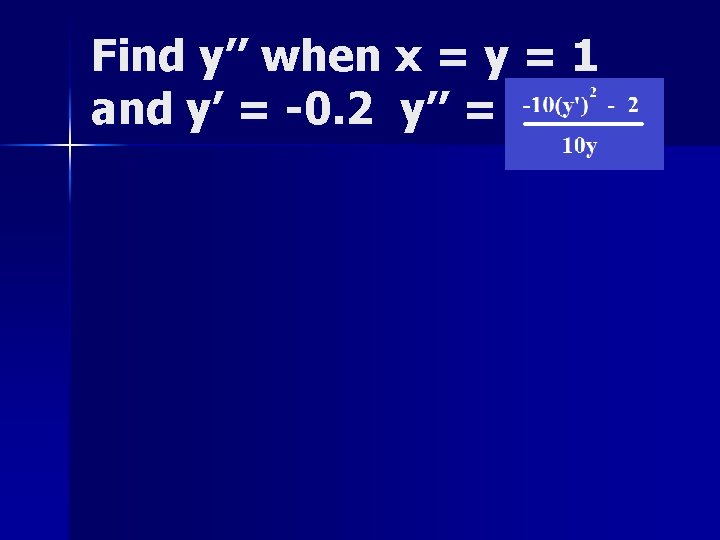
Find y’’ when x = y = 1 and y’ = -0. 2 y’’ =
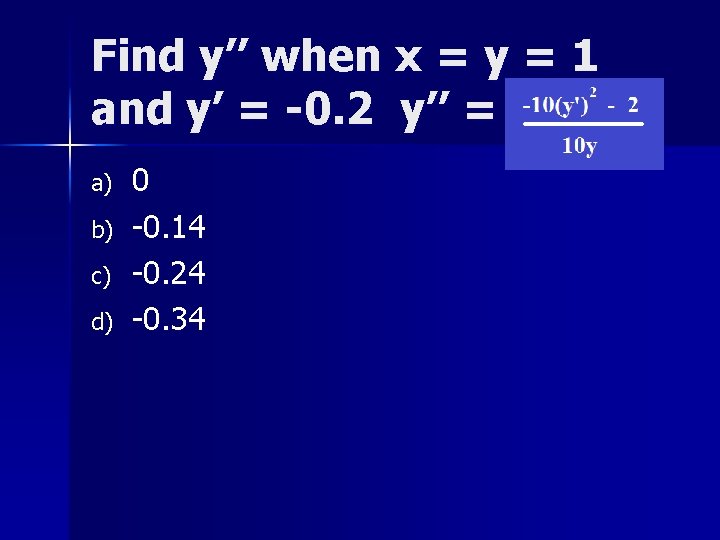
Find y’’ when x = y = 1 and y’ = -0. 2 y’’ = a) b) c) d) 0 -0. 14 -0. 24 -0. 34
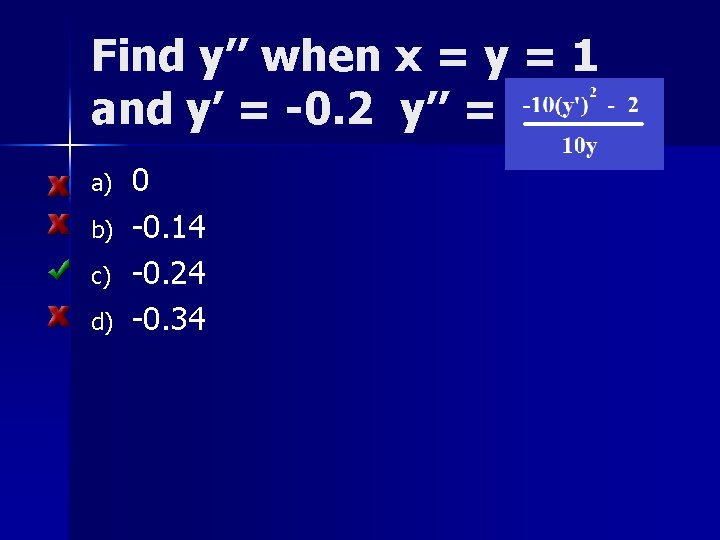
Find y’’ when x = y = 1 and y’ = -0. 2 y’’ = a) b) c) d) 0 -0. 14 -0. 24 -0. 34

Find dy/dx 1. x 2 y + y 2 x = 6 n 6. (3 xy + y)3 = 6 y n 11. x + tan(xy) = p + 1 at (p, ¼ ) n

Find the equation of the tangent and the normal 29. x 2 + xy - y 2 = 1 at (2, 3) n 31. x 2 y 2 = 9 at (1, 3) n 35. 2 xy + p sin(y) = 2 p at (1, p /2) n

Find the slope of n y 2 - sin( x + y ) = x 2 at the points (p/2, p/2) and (p/2, -p/2). n In other words, find the slopes of the two green lines. n

y 2 - sin( x + y ) = x 2 Let y stand for the two functions f 1 and f 2. Differentiating, 2 yy' - cos(x + y)[1+y'] = 2 x 2 yy’ – cos(x+y) y’ = 2 x [2 y - cos(x+y)]y' = 2 x + cos(x+y), or y' = [2 x + cos(x+y)] / [2 y - cos(x+y)]
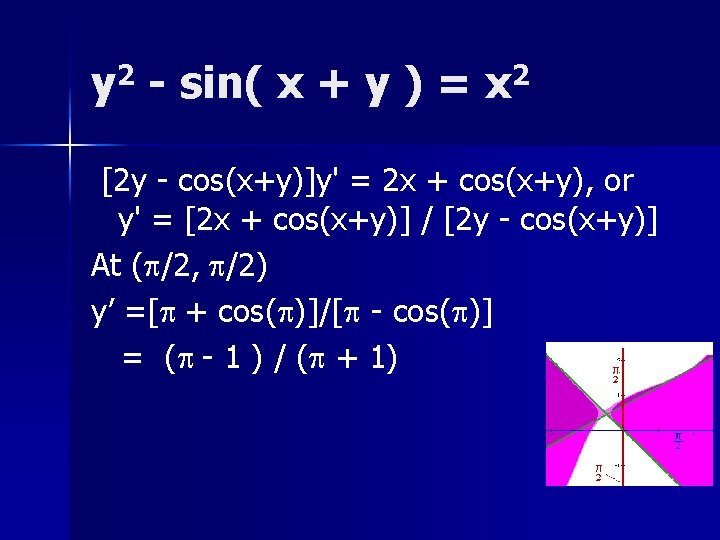
y 2 - sin( x + y ) = x 2 [2 y - cos(x+y)]y' = 2 x + cos(x+y), or y' = [2 x + cos(x+y)] / [2 y - cos(x+y)] At (p/2, p/2) y’ =[p + cos(p)]/[p - cos(p)] = (p - 1 ) / (p + 1)
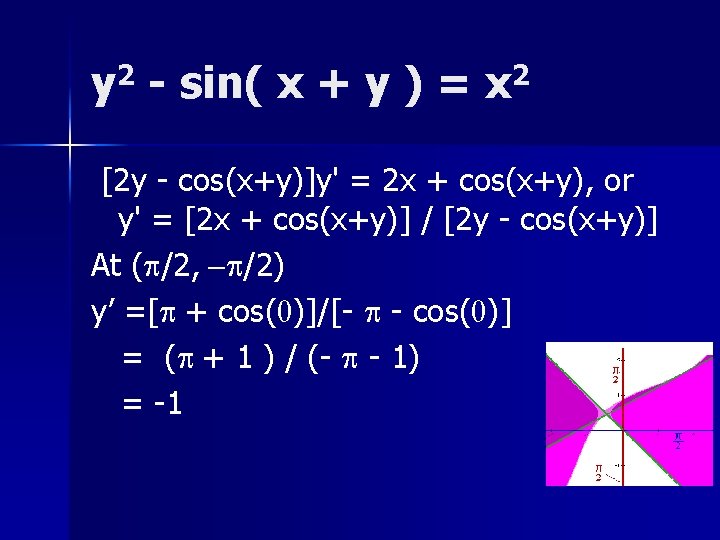
y 2 - sin( x + y ) = x 2 [2 y - cos(x+y)]y' = 2 x + cos(x+y), or y' = [2 x + cos(x+y)] / [2 y - cos(x+y)] At (p/2, -p/2) y’ =[p + cos(0)]/[- p - cos(0)] = (p + 1 ) / (- p - 1) = -1
![y2 xcosxy 2 ycosxy Find y at p2 p2 to one decimal 1 y’=[2 x+cos(x+y)] / [2 y-cos(x+y)] Find y’ at (-p/2, -p/2) to one decimal. 1.](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-53.jpg)
y’=[2 x+cos(x+y)] / [2 y-cos(x+y)] Find y’ at (-p/2, -p/2) to one decimal. 1. 933884414 0. 1

sin(y 2) = x 2 - y cos(y) Find y’ at the point (0, 0) cos(y 2)2 yy’ = 2 x – [-y sin(y) y’ + cos(y) y’] [cos(y 2)2 y - y sin(y) + cos(y)]y’=2 x (0 + 1) y’ = 0 so y’ = 0

sin(y 2) = x 2 - y cos(y) Find y’ at the point (. 5, 1. 65555) cos(y 2)2 yy’ = 2 x – [-y sin(y) y’ + cos(y) y’] [cos(y 2)2 y - y sin(y) + cos(y)]y’=2 x (-3. 04876 - 1. 64961 -0. 08465) y’ = 1 so y’ = -0. 2091

x 2 – 2 xy + y 2 sin(xy) > 4 Find y’ at the point (-2, 0) 2 x -2 xy’-2 y+y 2 cos(xy)[xy’+y]+2 sin(xy)yy’=0
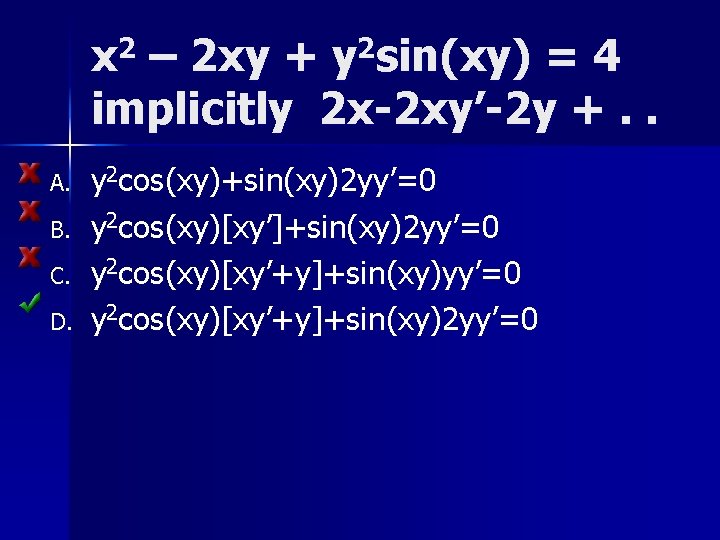
x 2 – 2 xy + y 2 sin(xy) = 4 implicitly 2 x-2 xy’-2 y +. . A. B. C. D. y 2 cos(xy)+sin(xy)2 yy’=0 y 2 cos(xy)[xy’]+sin(xy)2 yy’=0 y 2 cos(xy)[xy’+y]+sin(xy)2 yy’=0

x 2 – 2 xy + y 2 sin(xy) = 4 Find y’ at the point (-2, 0) 2 x -2 xy’-2 y+y 2 cos(xy)[xy’+y]+2 sin(xy)yy’=0 Next question is ‘Find y’ at the point (-2, 0). ’
![2 x 2 xy 2 yy 2 cosxyxyy2 sinxyyy0 Find y at 2 0 2 x -2 xy’ 2 y+y 2 cos(xy)[xy’+y]+2 sin(xy)yy’=0 Find y’ at (-2, 0)](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-59.jpg)
2 x -2 xy’ 2 y+y 2 cos(xy)[xy’+y]+2 sin(xy)yy’=0 Find y’ at (-2, 0) A. B. C. D. 0 1 2 -1
![Theorem If n is an integer xn nxn1 Use mathematical induction for positive Theorem – If n is an integer, [xn]’ =nxn-1 Use mathematical induction for positive](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-60.jpg)
Theorem – If n is an integer, [xn]’ =nxn-1 Use mathematical induction for positive n Use mathematical induction for nonnegative n n=0 ; 1’ = 0 Assume [xk]’ =kxk-1 for k<0 but fixed Prove [xk-1]’ =(k-1)xk-2
![Theorem If q is rational xq qxq1 Since q is rational there exist Theorem – If q is rational, [xq]’ =qxq-1 Since q is rational, there exist](https://slidetodoc.com/presentation_image_h/a75bb899bd9a59dba334df9dd407bbc0/image-61.jpg)
Theorem – If q is rational, [xq]’ =qxq-1 Since q is rational, there exist integers, m and n such that q = m/n and n is not 0. Then y = xq = xm/n and yn = xm thus nyn-1 y’ = m xm-1 y’ = qxq-1

Implicit Differentiation Related Rates x’ = dx/dx = 1 x’ = dx/dt

If the edge of a cube is decreasing at 2’/sec when x = 10’, n find the rate the volume is changing at that instant.

If the edge of a cube is decreasing at 2’/sec when x = 10’, find v’. v = x 3 n v’ = 3 x 2 n

If the edge of a cube is decreasing at 2’/sec when x = 10’, find v’. v = x 3 n v’ = 3 x 2 x’ n

If the edge of a cube is decreasing at 2’/sec when x = 10’, find v’. v = x 3 n v’ = 3 x 2 x’ n v’ = 3(100)(-2) = -600 cubic ft / sec n

Related Rates Read the problem, drawing a picture No non-constants on the picture Write an equation Differentiate implicitly Enter non-constants and solve

If the edge of a cube is decreasing at 2’/sec when x = 10’, n find the rate the volume is changing at that instant. 10 does not appear on the drawing n x=10 after v’ = 3 x 2 x’ n

Related Rates Suppose a painter is standing on a 13 foot ladder and Joe ties a rope to the bottom of the ladder and walks away at the rate of 2 feet per second.

Related Rates Suppose a painter is standing on a 13 foot ladder and Joe ties a rope to the bottom of the ladder and walks away at the rate of 2 feet per second. How fast is the painter falling when x = 5 feet?

Related Rates 13 is a constant and appears the rate of 2 feet per second [x’ = 2] How fast is the painter falling when x = 5 feet?

Related Rates 13 is a constant and appears the rate of 2 feet per second [x’ = 2] How fast is the painter falling when x = 5 feet? NOT ON THE DRAWING

What does the Pythagorean Theorem say about A. B. C. D. x 2 + y 2 = 13 2 x 2 + y 2 = 169 x 2 + 2 y 2 =13 x 2 + y 2 = 169

What does the Pythagorean Theorem say about A. B. C. D. x 2 + y 2 = 13 2 x 2 + y 2 = 169 x 2 + 2 y 2 =13 x 2 + y 2 = 169

Related Rates Write an equation Differentiate the equation implicitly 2 x x’ + 2 y y’ = 0 or xx’ + yy’ = 0 If Joe pulls at 2 ft. /sec. , find the speed of the painter when x = 5.

Find y when x = 5 A. B. C. D. 5 8 12 13

Find y when x = 5 A. B. C. D. 5 8 12 13

Related Rates Use algebra to find y. x 2 + y 2 = 169 52 + y 2 = 169 – 25 = 144 y = 12

2 x x’ + 2 y y’ = 0 or xx’ + yy’ = 0 Back to the calculus with y = 12, x = 5, and x’ = 2 ft/sec xx’ + yy’ =0 5(2) + 12(y’) = 0 y’ = -10/12 = -5/6 ft. /sec.

Related Rates Summary Even though Joe is walking 2 ft/sec, the painter is only falling -5/6 ft/sec. If the x and y values were reversed,

xx’ + yy’ =0 Find y’ if x’=2, y=5, and x = 12 A. B. C. D. -24/5 5/24 -5

xx’ + yy’ =0 Find y’ if x’=2, y=5, and x = 12 A. B. C. D. -24/5 5/24 -5

Related Rates Summary

Mo pulls in her small boat from a dock, 50’ high If she pulls at 2 ft per sec, how fast is the boat approaching the dock when it is 120 ft away?

E=IR If the voltage is decreasing at 4 v per second and R is a constant 5 ohms, find I’ ? If instead R is increasing at 6 ohms per sec, find I’ when E = 22, R = 5.

Related Rates Suppose air is entering a balloon at the rate of 25 cubic feet per minute. How fast is the radius changing when r = 30 feet?

Related Rates r’ = 0. 00221 ft per min

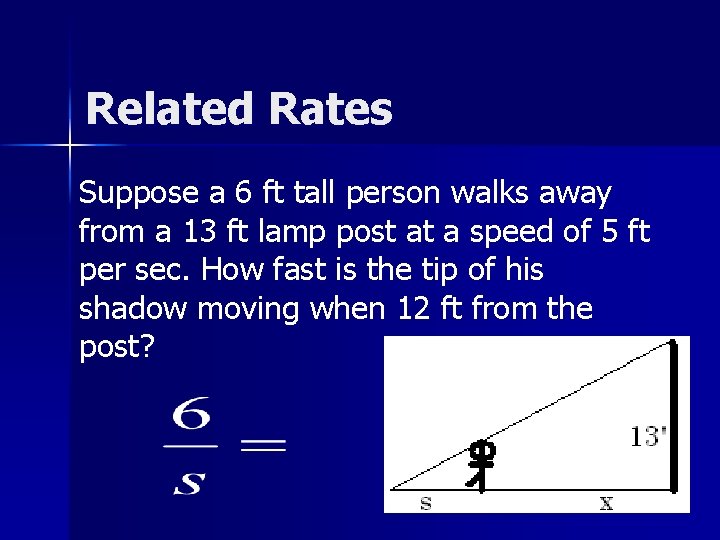
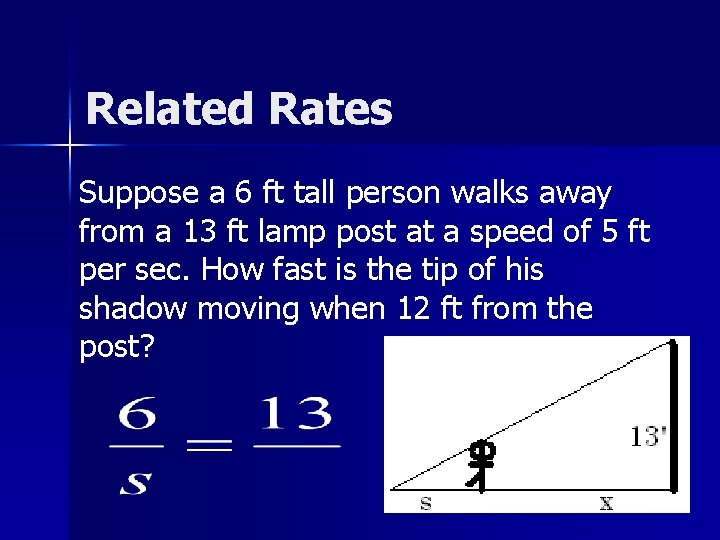
Related Rates Suppose a 6 ft tall person walks away from a 13 ft lamp post at a speed of 5 ft per sec. How fast is the tip of his shadow moving when 12 ft from the post?

Related Rates Suppose a 6 ft tall person walks away from a 13 ft lamp post at a speed of 5 ft per sec. How fast is the tip of his shadow moving when 12 ft from the post?

Find ? A. B. C. D. s x s+x 3

Find ? A. B. C. D. s x s+x 3

Related Rates The tip of the shadow has a speed of (s+x)’, not s’. What is s’ ? s’ is the growth of the shadow and includes getting shorter on the right.

Related Rates Cross multiplying Since x’ = 5

Related Rates Thus s’ is and Note that the tip is moving almost twice as fast as the walker, and more than twice as fast as the shadow regardless of x.

Related Rates Suppose a radar gun on first base catches a baseball 30 feet away from the pitcher and registers 50 feet per second. How fast is the ball really traveling?

a baseball 30 feet away from the pitcher and registers 50. feet per second. A. x=30 y’=50 B. C. D. x=30 y =50 x’=30 y’=50 x’=30 y=50

Related Rates The calculus. x = 30 y’ = 50 y = ? The algebra.

Differentiate implicitly A. B. C. D. 2 x = 2 y y’ 2 x = y y’ 2 x x’ = 2 y y’

Differentiate implicitly A. B. C. D. 2 x = 2 y y’ 2 x = y y’ 2 x x’ = 2 y y’

Related Rates x = 30 y’ = 50 y = ? Back to the calculus.

Related Rates Back to the calculus. x = 30 y’ = 50 y = ?

Related Rates Back to the calculus. x = 30 y’ = 50 y = ?

a baseball 30 feet away from the pitcher and registers 50. feet per second. A. B. C. D. x’ = 0. 6 root(4950) x’ = 50 root(4950) x’ = 30 root(4950) x’ = 5/3 root(4950)

a baseball 30 feet away from the pitcher and registers 50. feet per second. A. B. C. D. x’ = 0. 6 root(4950) x’ = 50 root(4950) x’ = 30 root(4950) x’ = 5/3 root(4950)

Related Rates x’ = 117. 260 feet/sec. X = 30 y’ = 50 y = ?

Related Rates Read the problem, drawing a picture No non-constants on the picture Write an equation Differentiate implicitly Enter non-constants and solve