Implicit differentiation Implicit differentiation is used to differentiate












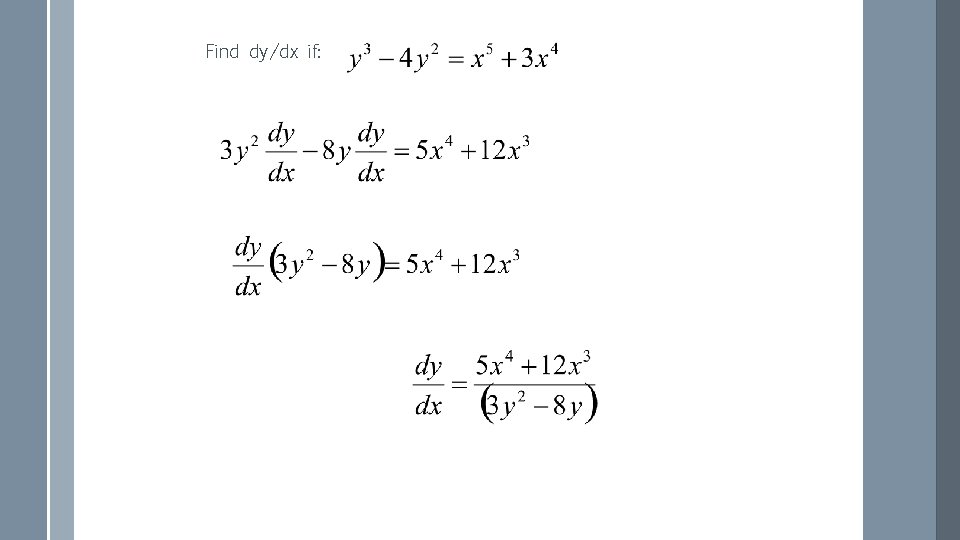





- Slides: 26

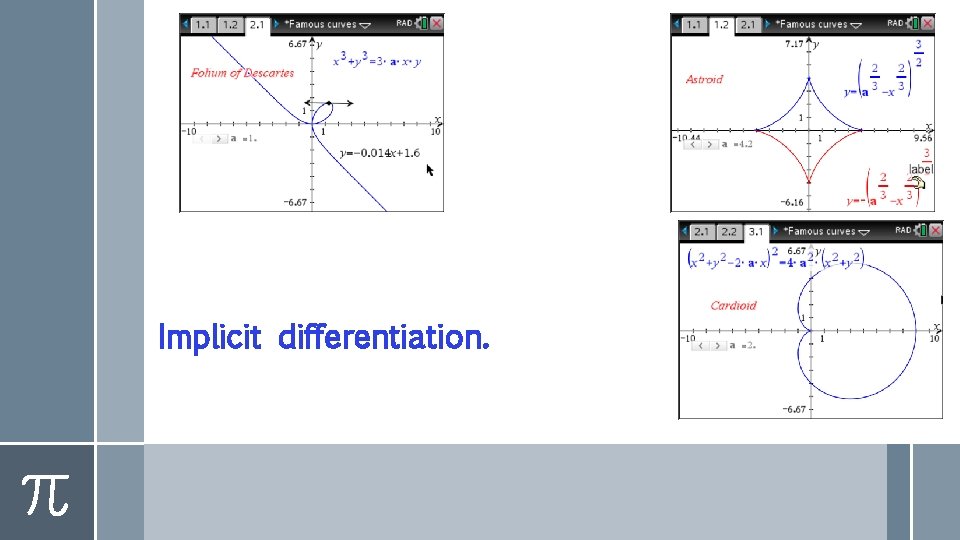
Implicit differentiation.

Implicit differentiation is used to differentiate implicit relations.

Implicit Differentiation So far, all the equations and functions we looked at were all stated explicitly in terms of one variable: In this function, y is defined explicitly in terms of x. If we re-wrote it as xy = 1, y is now defined implicitly in terms of x. It is easy to find the derivative of an explicit function, but what about:

How would you find the derivative in the equation x 2 – 2 y 3 + 4 y = 2 where it is very difficult to express y as a function of x? To do this, awe use a procedure called implicit differentiation. This means that when we differentiate terms involving x alone, we can differentiate as usual. But when we differentiate terms involving y, we must apply the Chain Rule. Watch the examples very carefully!!!

An Implicit function is one where the variable “y” can not be easily solved for in terms of only “x” as in he following examples:

Find by implicit differentiation for each of the following relationships:

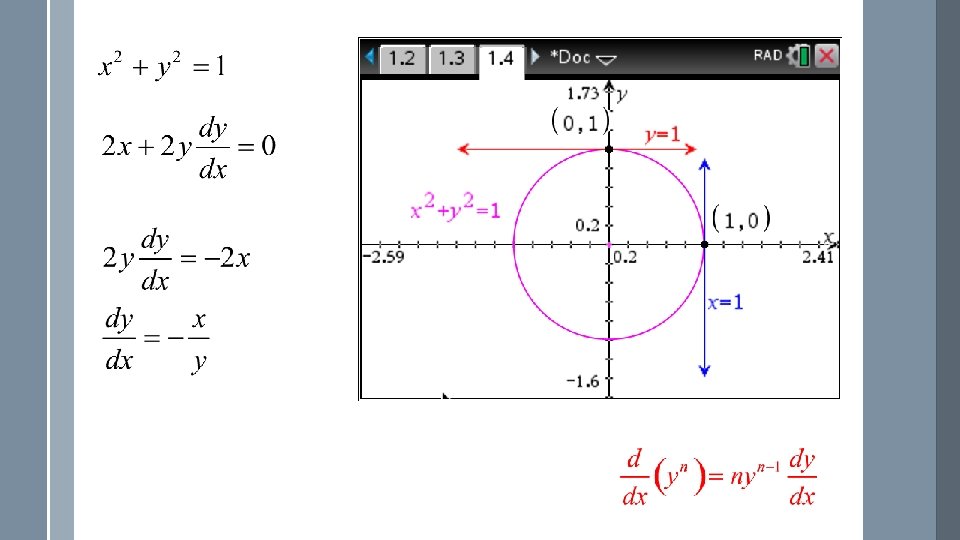
We differentiate each term Whenever we differentiate a term with y we need to have dy/dx next to it.

We differentiate each term Whenever we differentiate a term with y we need to have dy/dx next to it. Notice that dy/dx is in terms of both x and y. Discuss the value of the gradient at (0, 0) undefined

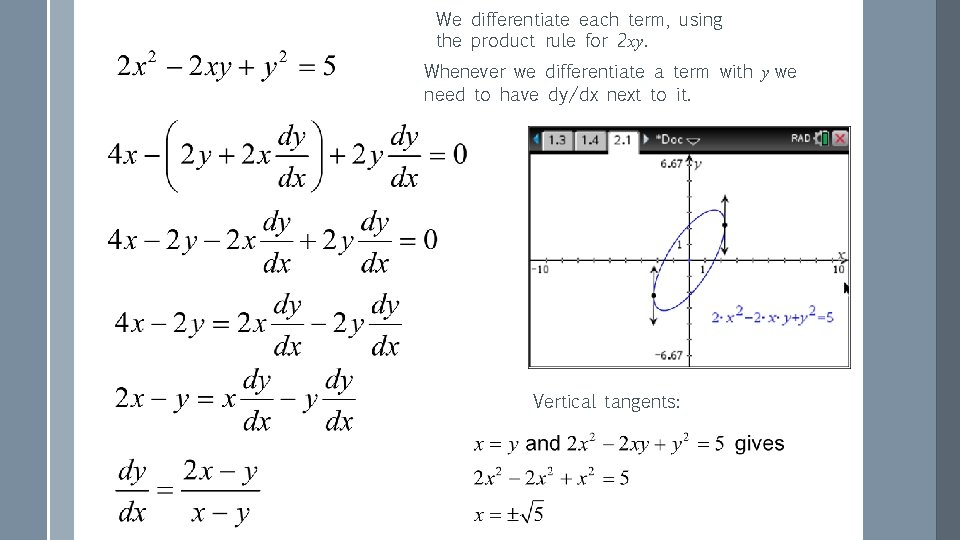
We differentiate each term, using the product rule for xy. Whenever we differentiate a term with y we need to have dy/dx next to it. Notice that dy/dx is in terms of both x and y.

We differentiate each term Whenever we differentiate a term with y we need to have dy/dx next to it. It is a circle. Discuss vertical and horizontal tangents.

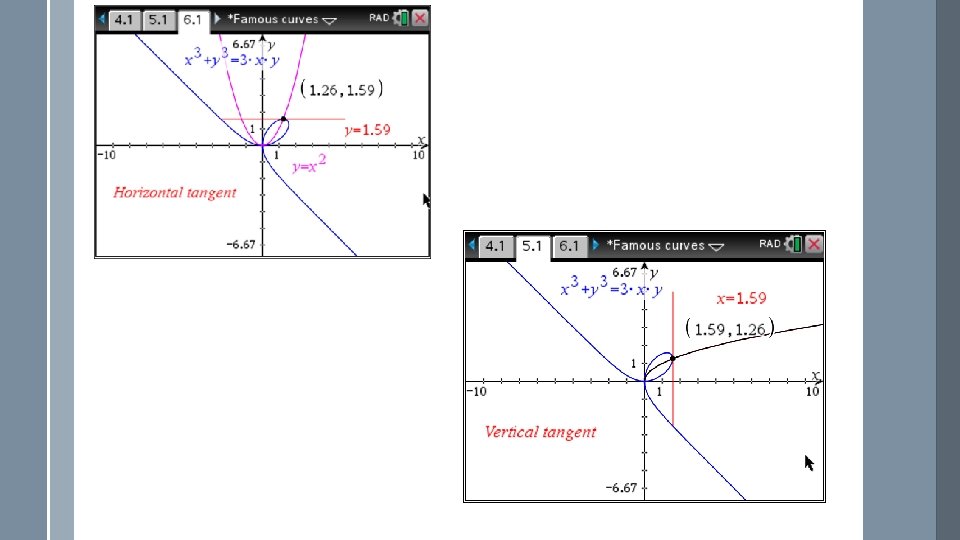
We differentiate each term, using the product rule for 2 xy. Whenever we differentiate a term with y we need to have dy/dx next to it. Vertical tangents:

(a) by explicit differentiation (making y the subject). (b) by implicit differentiation.



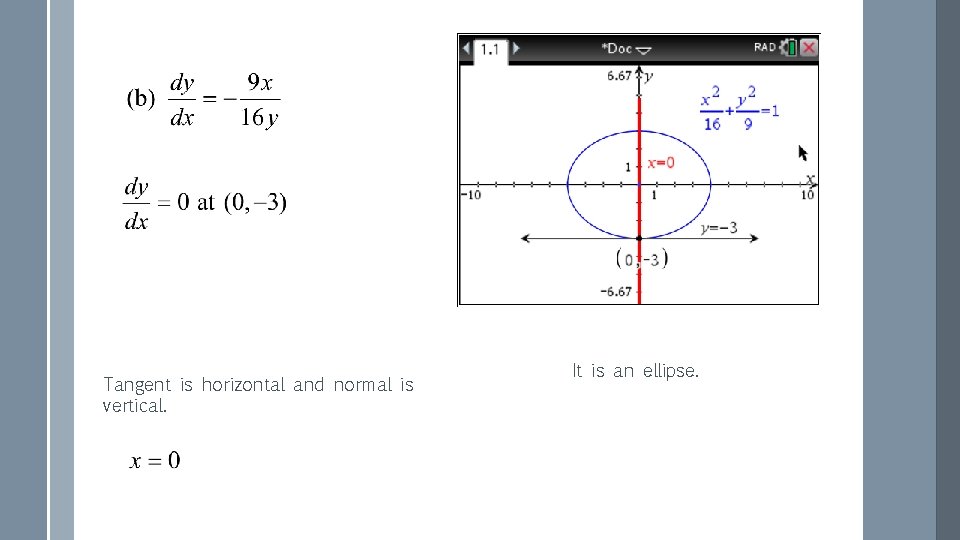
Tangent is horizontal and normal is vertical. It is an ellipse.

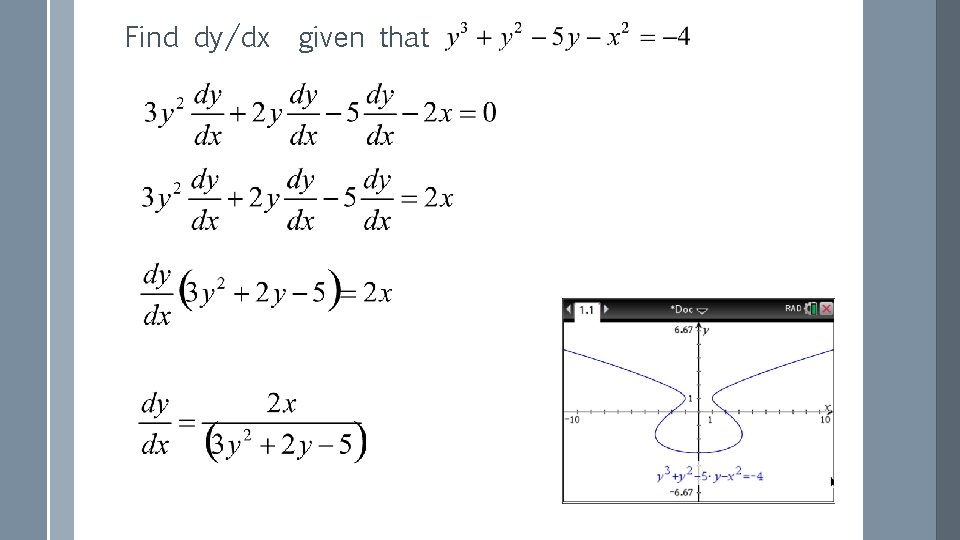
Find dy/dx given that

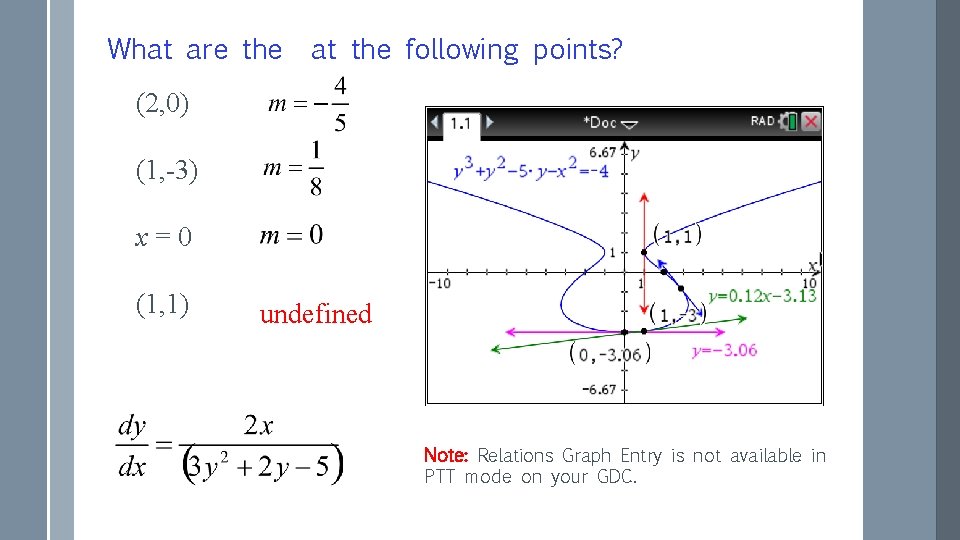
What are the at the following points? (2, 0) (1, -3) x=0 (1, 1) undefined Note: Relations Graph Entry is not available in PTT mode on your GDC.


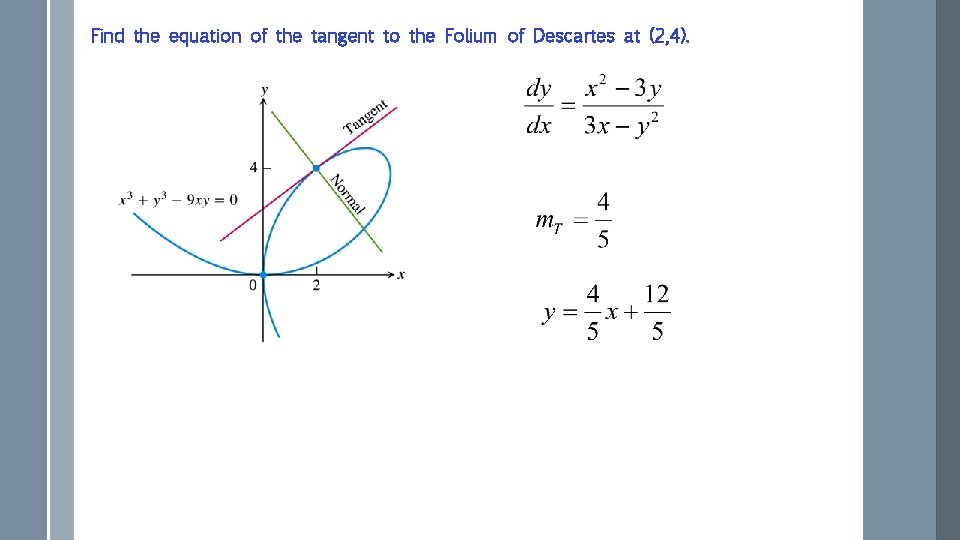
Find the equation of the tangent to the Folium of Descartes at (2, 4).

This can’t be solved for y.
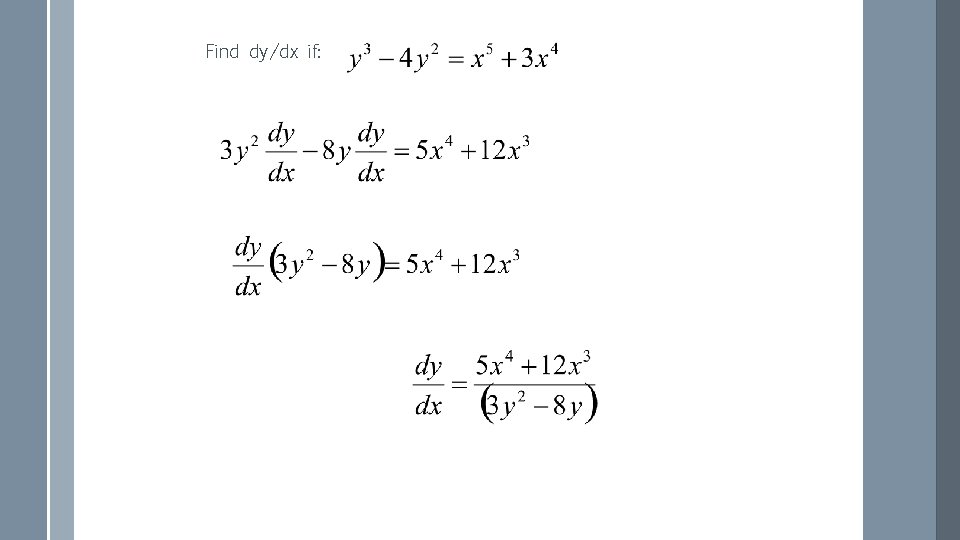
Find dy/dx if:

Find dy/dx if: Chain Rule

Find dy/dx if: Product Rule!

Find the equations of the lines tangent and normal to the curve. We need the slope. at Since we can’t solve for y, we use implicit differentiation to solve for Note product rule. .

Find the equations of the lines tangent and normal to the curve at . tangent: normal: Normal line is perpendicular to tangent

Higher Order Derivatives Find if . Substitute back into the equation.
 How to implicit differentiation
How to implicit differentiation Explicit vs implicit equations
Explicit vs implicit equations Diff of sec^2x
Diff of sec^2x Constant multiple rule examples
Constant multiple rule examples Instead 접속사
Instead 접속사 Implicit differentiation
Implicit differentiation Intermediate variable
Intermediate variable Implicit differentiation and related rates
Implicit differentiation and related rates Chain rule and implicit differentiation
Chain rule and implicit differentiation Implicit differentiation with inverse trig functions
Implicit differentiation with inverse trig functions Implicit differentiation formula
Implicit differentiation formula Explicit differentiation
Explicit differentiation In a premix burner used in fes the fuel used is
In a premix burner used in fes the fuel used is In a premix burner used in fes the fuel used is
In a premix burner used in fes the fuel used is Differentiate between racemic mixture and meso compound
Differentiate between racemic mixture and meso compound Rigor mortis vs cadaveric spasm
Rigor mortis vs cadaveric spasm Differentiate wetland and dryland preparation
Differentiate wetland and dryland preparation Differentiate between soldering brazing and welding
Differentiate between soldering brazing and welding Difference between modernisation and globalisation
Difference between modernisation and globalisation Differentiate sentences
Differentiate sentences Trim and stability
Trim and stability Indeterminate error
Indeterminate error Differentiate between physical and chemical change
Differentiate between physical and chemical change Russian formalism
Russian formalism Open and closed system in thermodynamics
Open and closed system in thermodynamics Difference between a star and ao star
Difference between a star and ao star Differentiate from first principles
Differentiate from first principles