Differentiation Implicit KUS objectives BAT Understand Implicit differentiation

Differentiation: Implicit • KUS objectives BAT Understand Implicit differentiation and find the gradient function for functions in x and y Starter differentiate:

Notes Implicit differentiation of single terms For some equations it is impossible to rearrange to give y = f(x) and hence differentiate. One approach is to use the chain rule to differentiate each term without rearrangement For example differentiate y 2 More examples:

WB 30 a One approach is to use the chain rule to differentiate each term without rearrangement. Here are some Key examples: Term Gradient function

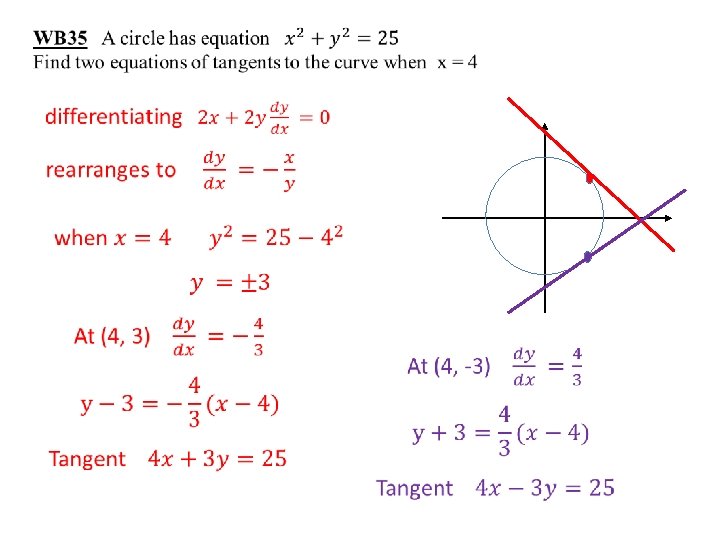
Notes Implicit differentiation of functions Now we can differentiate an entire function with ‘mixed terms’ in x and y And attempt to rearrange the result to find a gradient function For example the equation of this circle By differentiating each term implicitly Then rearranging We get a gradient function in terms of x and y

WB 31 Differentiate the given functions function Gradient function

You now have a formula for the gradient, but in terms of x AND y, not just x b) at the point (1, 1)

Notes Implicit differentiation of functions A special case is the derivative of a product of x and y

WB 33 abc Differentiate the given functions (including products) function Gradient function

WB 33 de Differentiate the given functions (including products) function Gradient function

WB 33 fg Differentiate the given functions (including products) function Gradient function

You now have a formula for the gradient, but in terms of x AND y, not just x b) at the point (1, 2)

M 1 A 1 A 1 M 1 A 1

KUS objectives BAT Understand Implicit differentiation and find gradient function for functions in x and y Crucial points Make sure that you understand the process of differentiating an equation implicitly Write one thing you have learned Write one thing you need to improve

END