Implicit Differentiation 3 5 Explicit vs Implicit Functions

Implicit Differentiation 3. 5

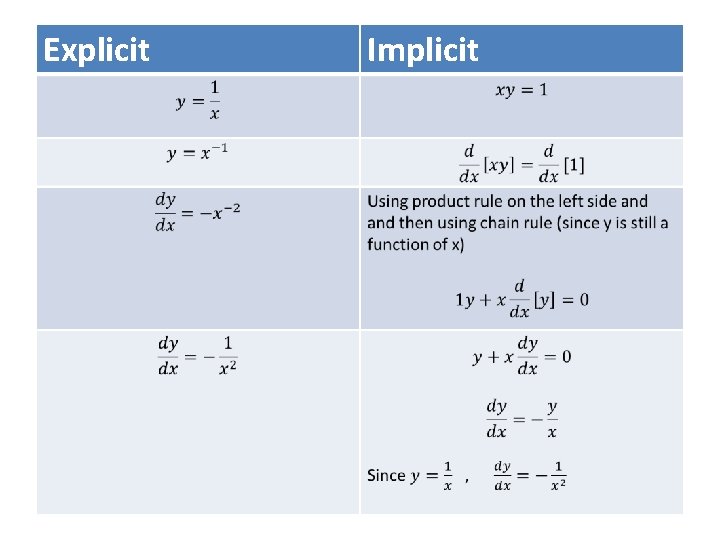
Explicit vs. Implicit Functions •

Explicit Implicit Explicit Vs. Implicit cont.

Differentiating with respect to x • Variables agree Use power rule Variables disagree Use chain rule Product Rule Chain Rule Simplify

Implicit Differentiation Steps •

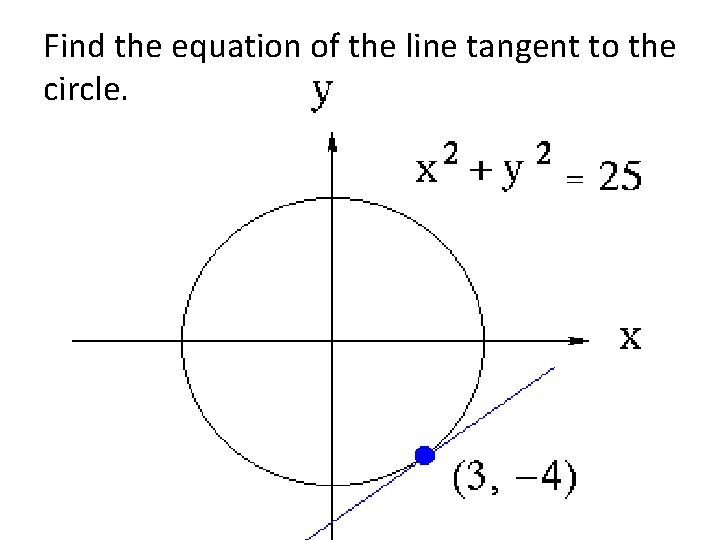
Find the equation of the line tangent to the circle.

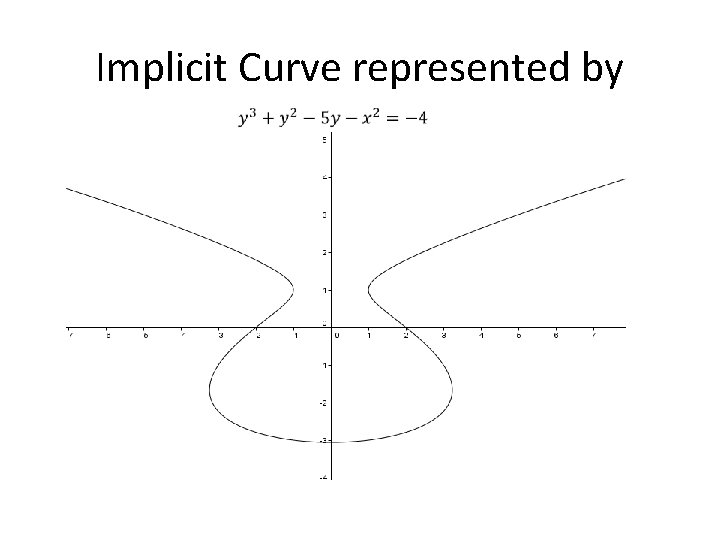
Implicit Curve represented by

Graphs of differentiable functions •

Find the Second Derivative •

Finding a line tangent to a graph •

Determine the slope of the tangent line to the graph •

Hw • Day 1 page 172 • 1 -19 odd, 25, 27, 29, • Day 2 • 35 -38, 43 -46, 67, 69, 70

Implicit Differentiation Continued “You had me until the Lemniscate”

Quick Recap • Implicit Equations are equations that can be messy to rewrite as functions so sometimes we differentiate first and rewrite as functions later. • Mostly this is when we have x and y on the same side and y raised to some exponent

Still Recapping • We use the derivative as an operation on each piece of the equation we can. Taking the derivative of an x value with respect to x works normally. • Taking the derivative of y values with respect to x we have to use chain rule (ie write dy/dx next to everything) since y is still a function of x. • Finally solve the equation for

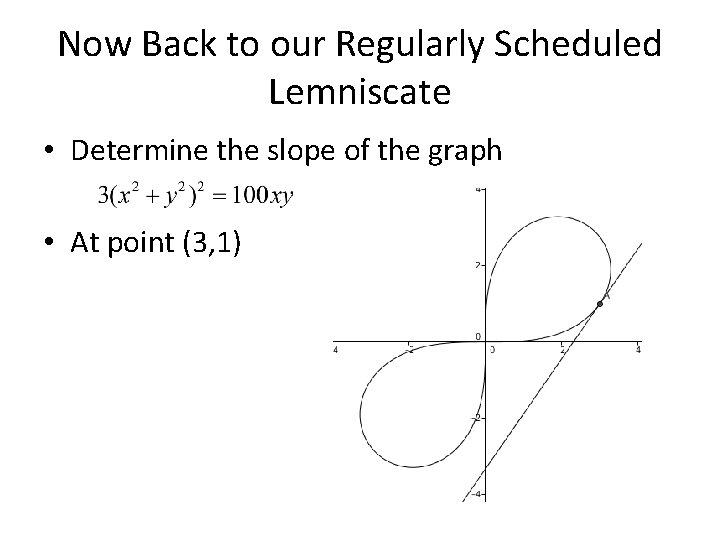
Now Back to our Regularly Scheduled Lemniscate • Determine the slope of the graph • At point (3, 1)

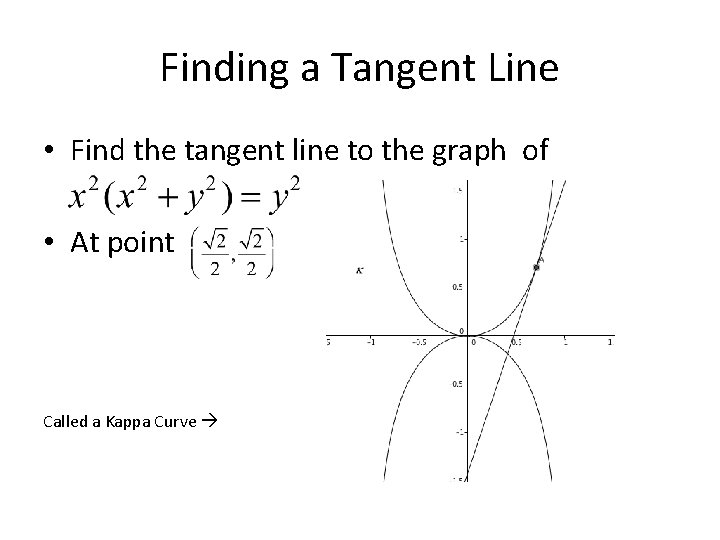
Finding a Tangent Line • Find the tangent line to the graph of • At point Called a Kappa Curve

Finding the Second Derivative of an implicit equation • Given • Find

Logarithmic Differentiation • We were able to use logarithmic properties to help us when we were taking the logarithm of a messy function. If we are not already dealing with the logarithm of a function, we can take the logarithm of both sides and use implicit differentiation.

Steps 1) Take the natural logarithm of both sides 2) Use logarithmic properties to simplify 3) Use implicit differentiation 4) Simplify and solve for the derivative with respect to x • 5) Substitute your original equation for y • •

Find dy/dx for sin y = x • Once we have found the derivative we can restrict the domain and doing so find the derivative for arcsin (x).

Hw Page 172 • 25, 27, 32, 34, 35, 37, 43, 45, 67, 69, 70