Sec 3 5 IMPLICIT DIFFERENTIATION Example In some










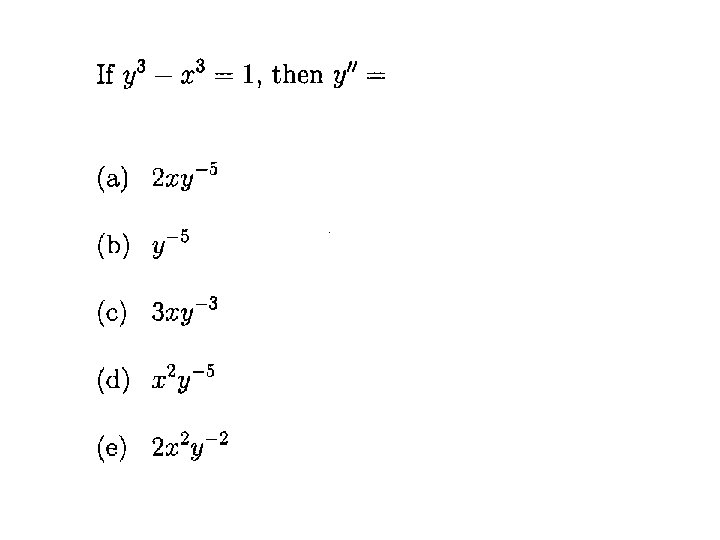





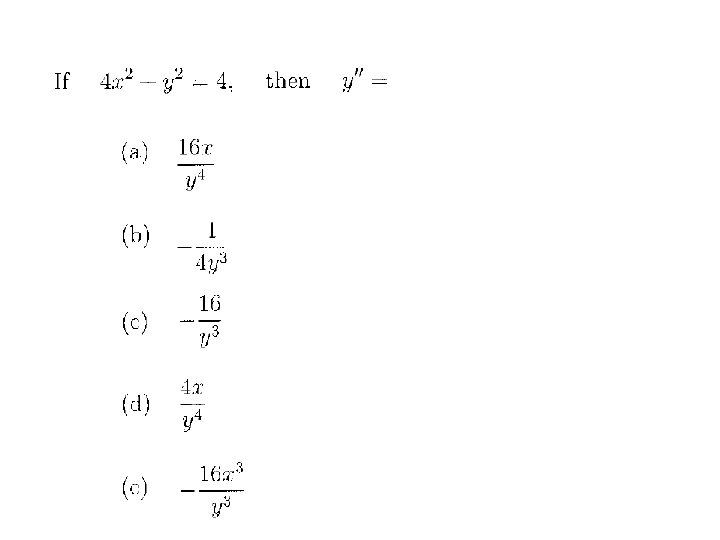
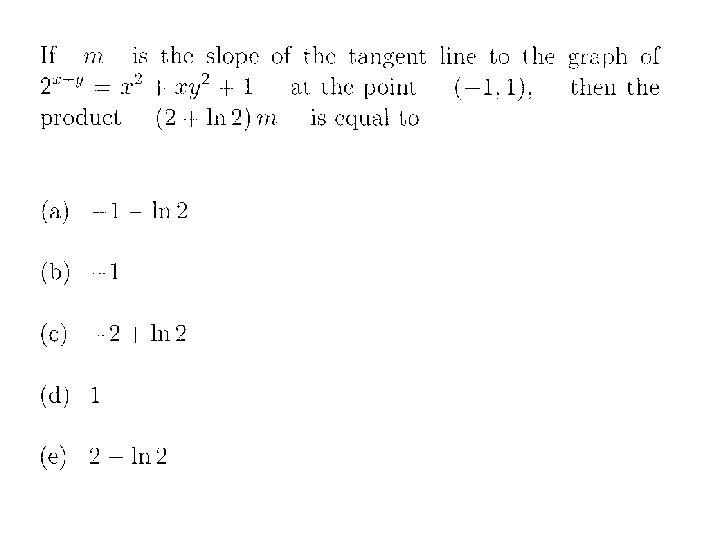

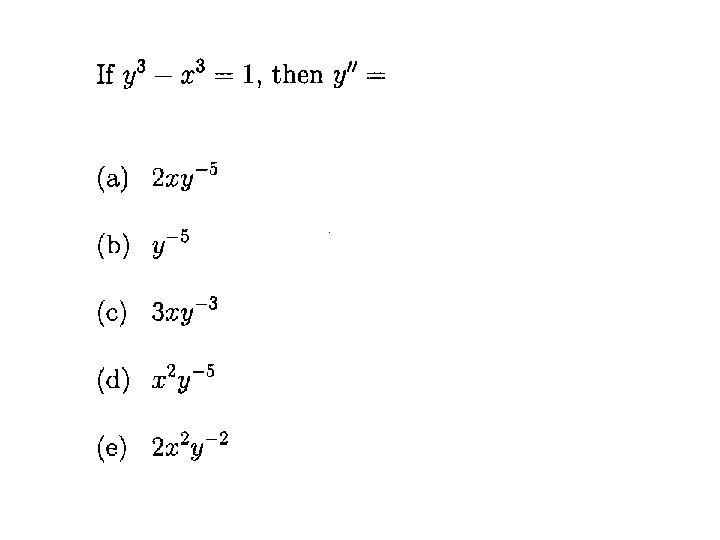
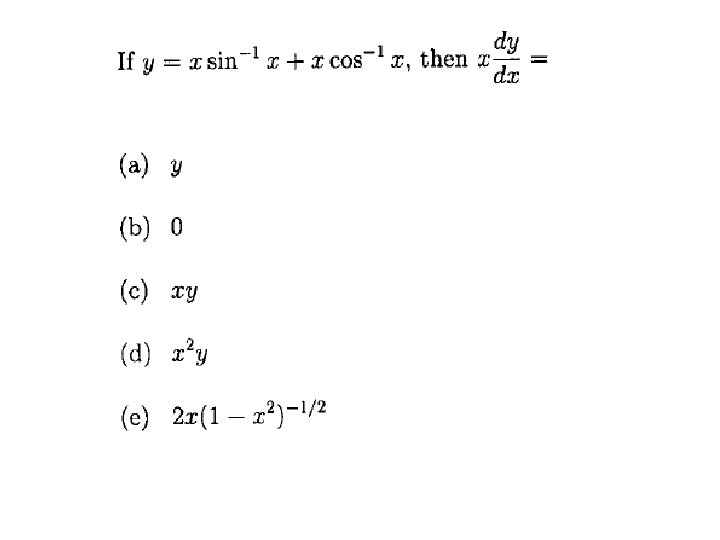
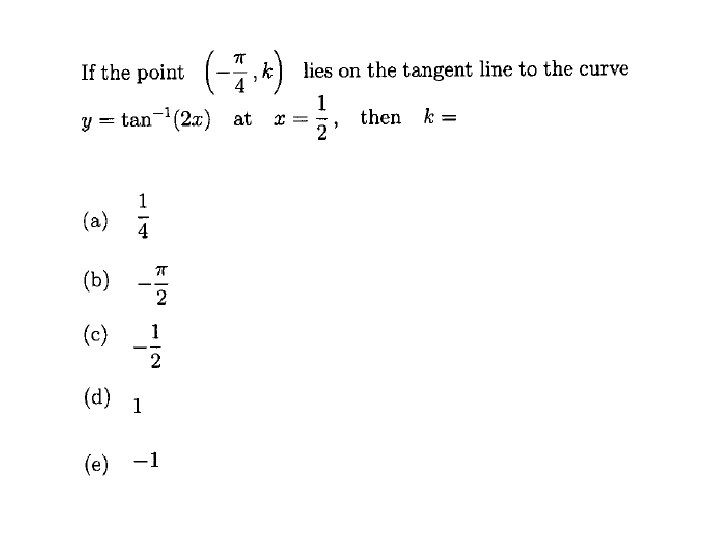
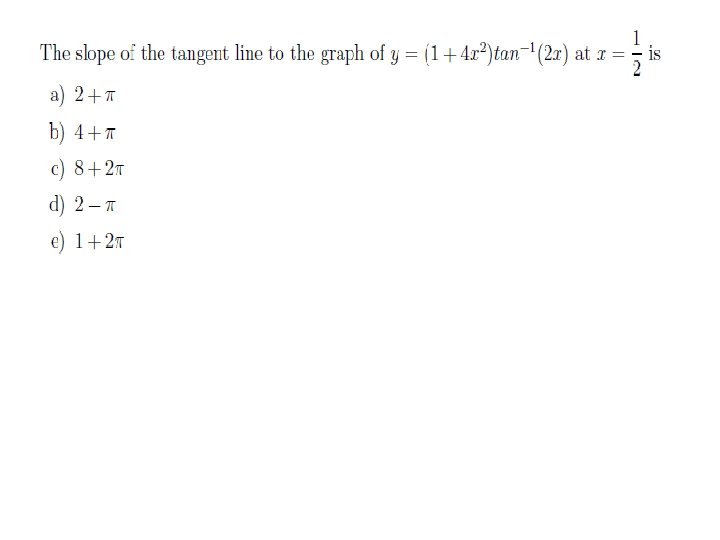
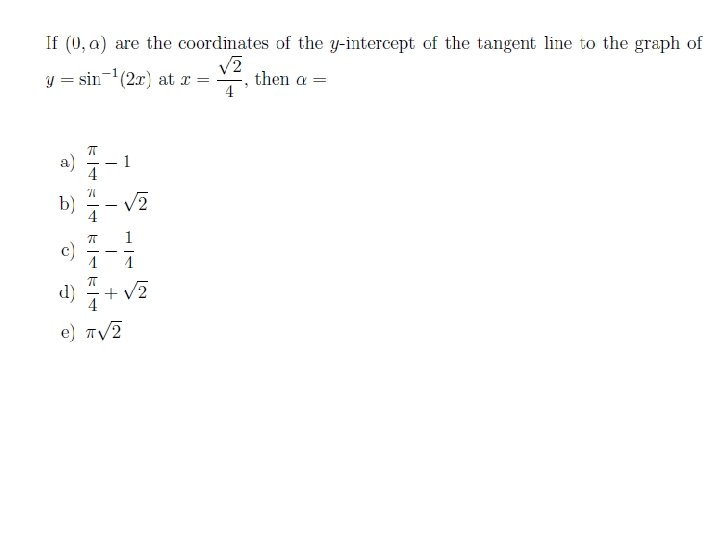
- Slides: 24

Sec 3. 5: IMPLICIT DIFFERENTIATION Example: In some cases it is possible to solve such an equation for as an explicit function Example: In many cases it is difficult (impossible to write y in terms of x) Fortunately, we don’t need to solve an equation for in terms of in order to find the derivative of. Instead we can use the method of implicit differentiation This consists of differentiating both sides of the equation with respect to x and then solving the resulting equation for y’.

Sec 3. 5: IMPLICIT DIFFERENTIATION This consists of differentiating both sides of the equation with respect to x and then solving the resulting equation for y’. Remember: y is a function of x and using the Chain Rule, Example:

Sec 3. 5: IMPLICIT DIFFERENTIATION This consists of differentiating both sides of the equation with respect to x and then solving the resulting equation for y’. Remember: y is a function of x and using the Chain Rule, Example:

Sec 3. 5: IMPLICIT DIFFERENTIATION This consists of differentiating both sides of the equation with respect to x and then solving the resulting equation for y’. Remember: y is a function of x and using the Chain Rule,

Sec 3. 5: IMPLICIT DIFFERENTIATION Example: Remember: In finding y’’ you may use the original equation fat circle

Sec 3. 5: IMPLICIT DIFFERENTIATION DERIVATIVES OF TRIGONOMETRIC FUNCTIONS: DERIVATIVES OF INVERSE TRIGONOMETRIC FUNCTIONS:

Sec 3. 5: IMPLICIT DIFFERENTIATION means differentiate implicitly

Sec 3. 5: IMPLICIT DIFFERENTIATION


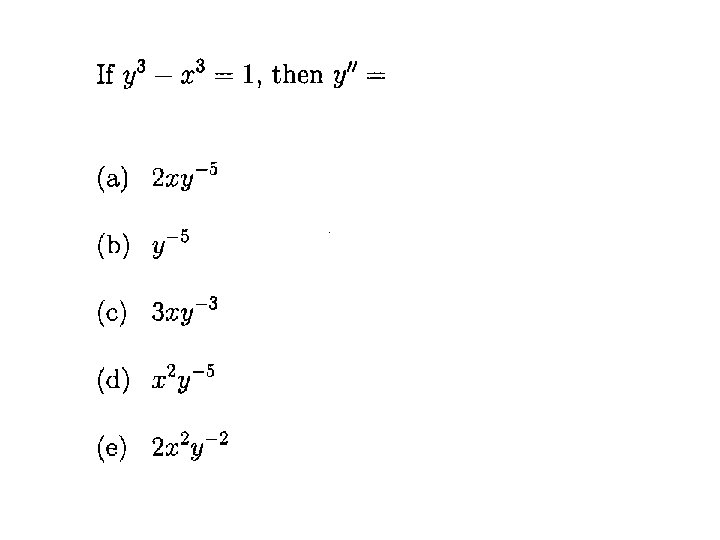





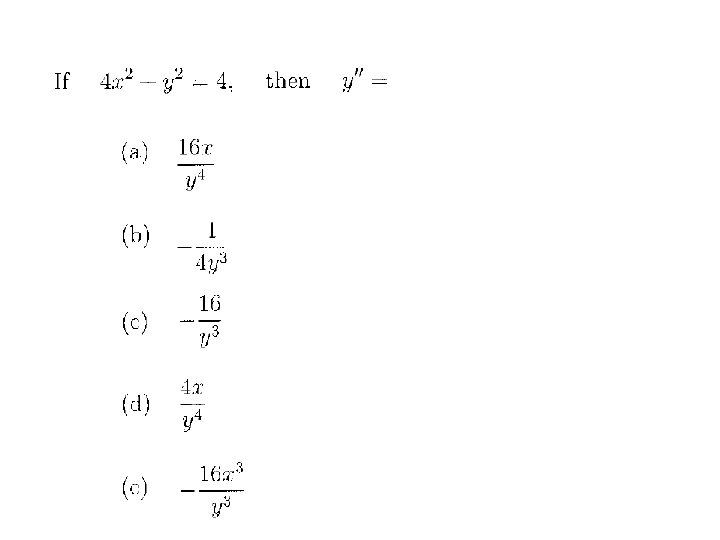
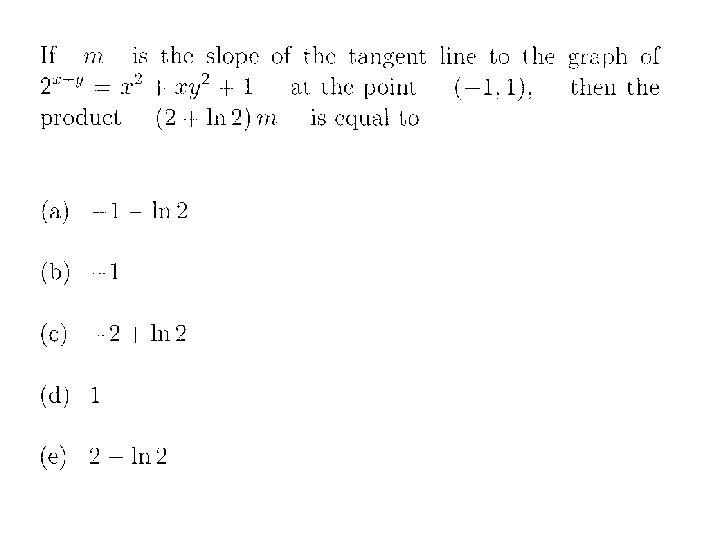

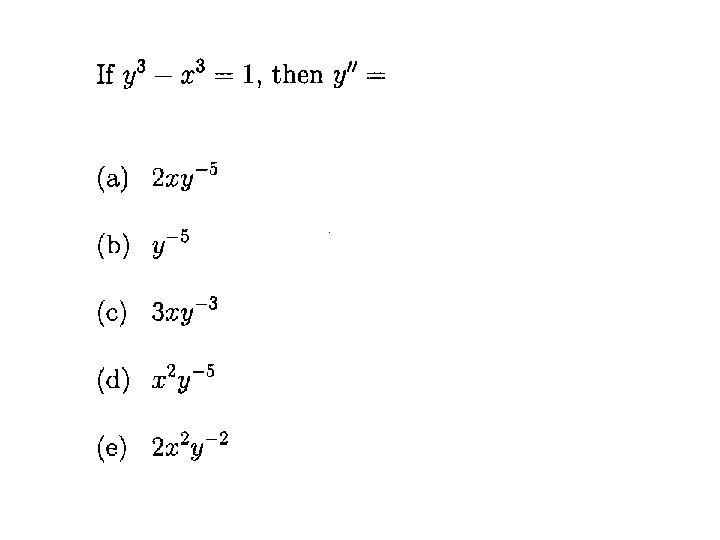
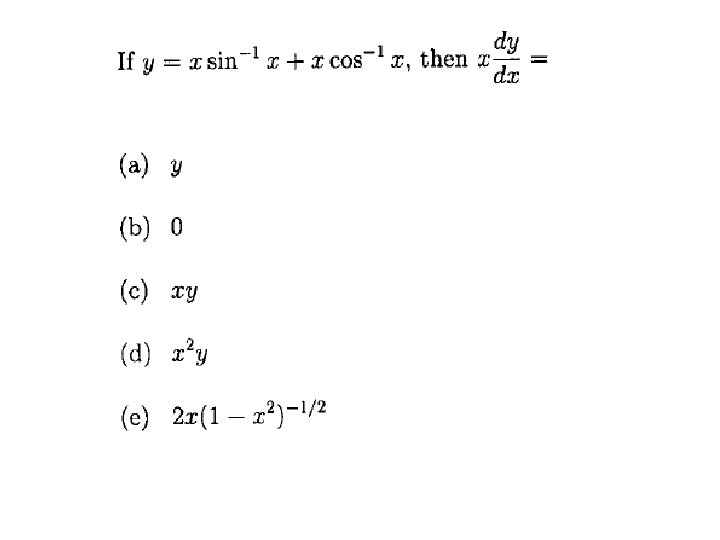
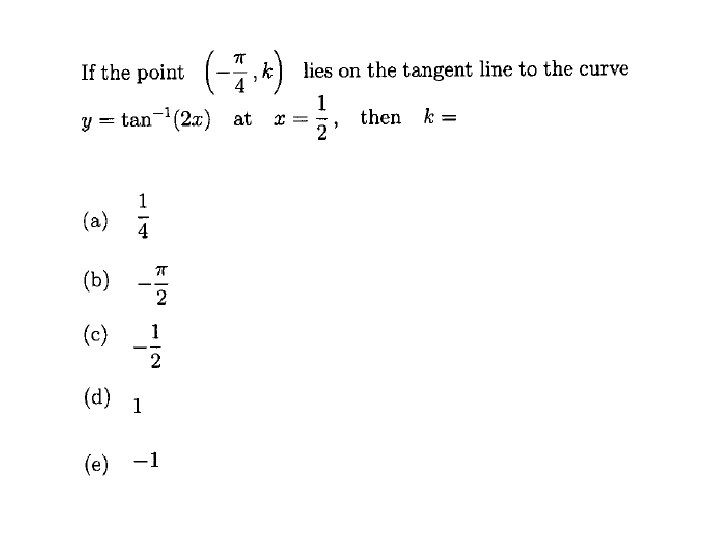
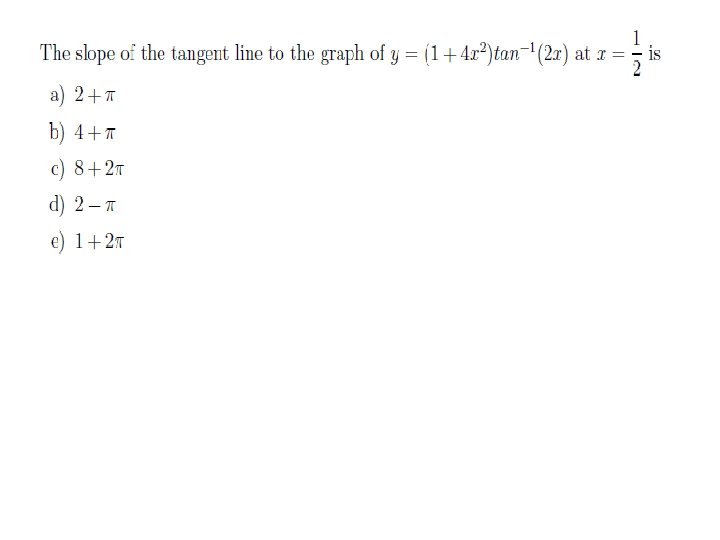
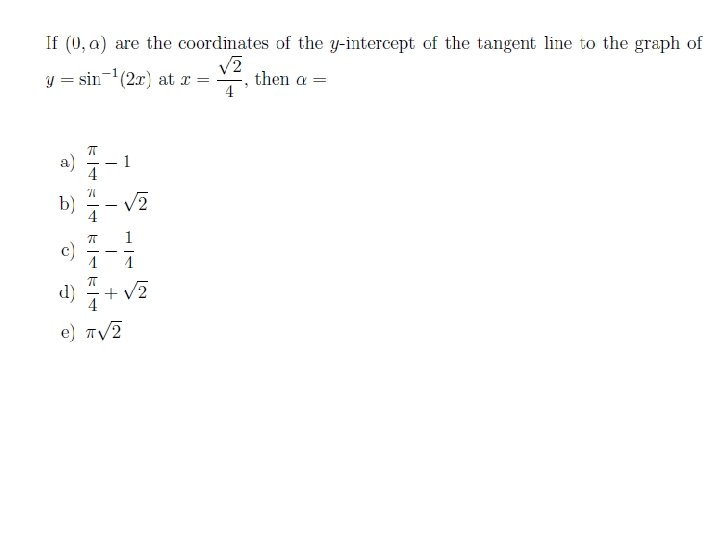
 Derivative implicit
Derivative implicit Diff of sec^2x
Diff of sec^2x Implicit differentiation formula
Implicit differentiation formula Xy implicit differentiation
Xy implicit differentiation Explicit differentiation
Explicit differentiation Differentiation of implicit function
Differentiation of implicit function Derivative of exponential
Derivative of exponential Intermediate variable
Intermediate variable Implicit differentiation with inverse trig functions
Implicit differentiation with inverse trig functions Implicit vs explicit differentiation
Implicit vs explicit differentiation Instead 접속사
Instead 접속사 Implicit differentiation and related rates
Implicit differentiation and related rates Derivative of arccos
Derivative of arccos Sometimes you win some
Sometimes you win some Sometimes you win some sometimes you lose some
Sometimes you win some sometimes you lose some Ice cream countable
Ice cream countable Contact and noncontact forces
Contact and noncontact forces Some say the world will end in fire some say in ice
Some say the world will end in fire some say in ice Some say the world will end in fire some say in ice
Some say the world will end in fire some say in ice Some trust in horses
Some trust in horses How many sentences in english
How many sentences in english Implicit memory
Implicit memory Explicit memory psychology example
Explicit memory psychology example Implicit of the grass was green
Implicit of the grass was green Implicit information is not written in the text
Implicit information is not written in the text











































