2014 Implicit Differentiation Calculus BC Implicit Differentiation Equation

2014 Implicit Differentiation Calculus BC

Implicit Differentiation Equation for a line: Explicit Form <One variable given explicitly in terms of the other> Implicit Form <Function implied by the equation> Differentiate the Explicit < Explicit: , y is function of x > Differentiation taking place with respect to x. The derivative is explicit also.

Implicit Differentiation Equation of circle: To work explicitly; must work two equations Implicit Differentiation is a Short Cut - A method to handle equations that are not easily written explicitly. ( Usually non-functions)

Implicit Differentiation Find the derivative with respect to x < Assuming - y is a differentiable function of x > Chain Rule Pretend y is some function like so becomes (A) (B) (C) Note: Use the Leibniz form. Leads to Parametric and Related Rates.

Implicit Differentiation (D) Product Rule (E) Chain Rule

Implicit Differentiation To find implicitly. EX: Diff Both Sides of equation with respect to x Solve for

EX 1: (a) Find the derivative at the point ( 5, 3 ) , at ( -1, -3 ) (b) Find where the curve has a horizontal tangent. (c) Find where the curve has vertical tangents.

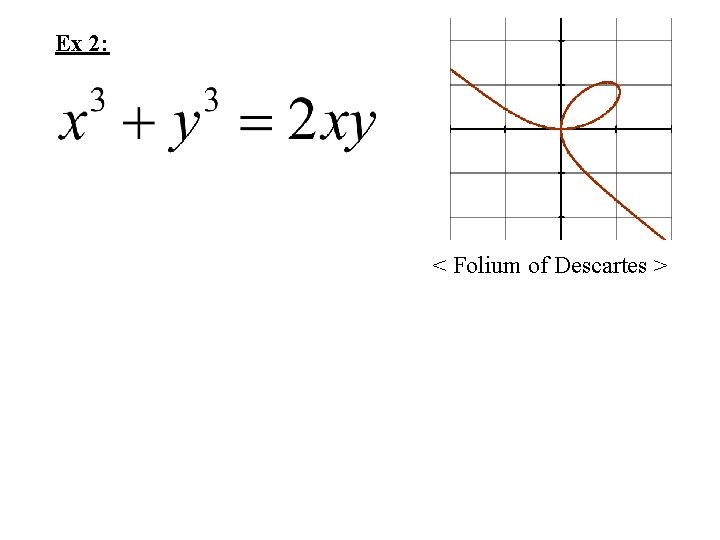
Ex 2: < Folium of Descartes >

Why Implicit? Explicit Form: < Folium of Descartes >

Ex 2 Graph: < Folium of Descartes > Parametric Form: Plot the Folium of Descartes on your graphing calculator and determine the portion of the folium generated when (a) t < -1 ; (b) -1 < t 0 ; (c) t > 0

2 nd Derivatives EX: Our friendly circle. Find the 2 nd Derivative. NOTICE: The second derivative is in terms of x , y , AND dy /dx. The final step will be to substitute back the value of dy / dx into the second derivative.

2 nd Derivatives EX: Find the 2 nd Derivative.

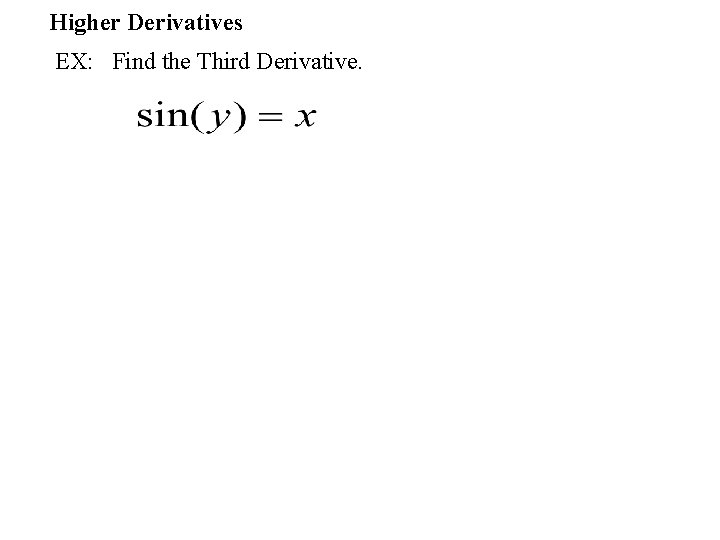
Higher Derivatives EX: Find the Third Derivative.

Last update • 10/19/10 Øp. 162 11 – 29 odd