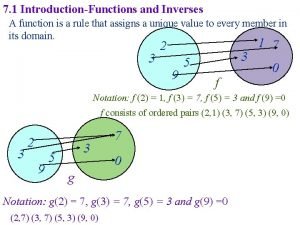
DERIVATIVE OF A FUNCTION is called the derivative
























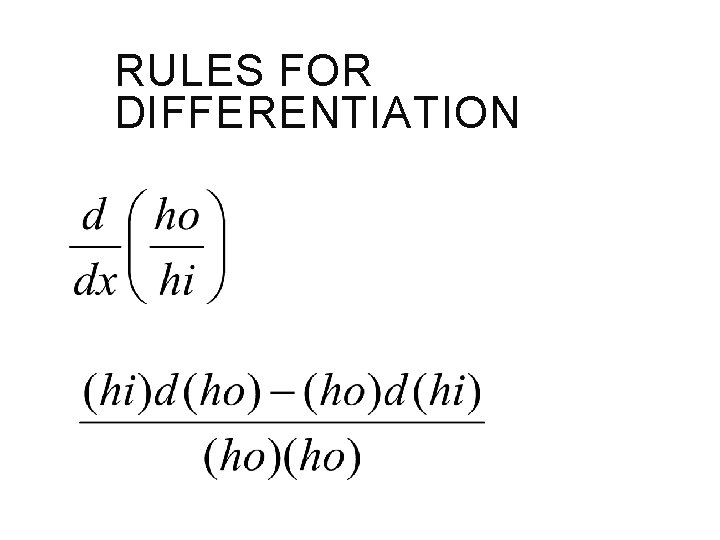












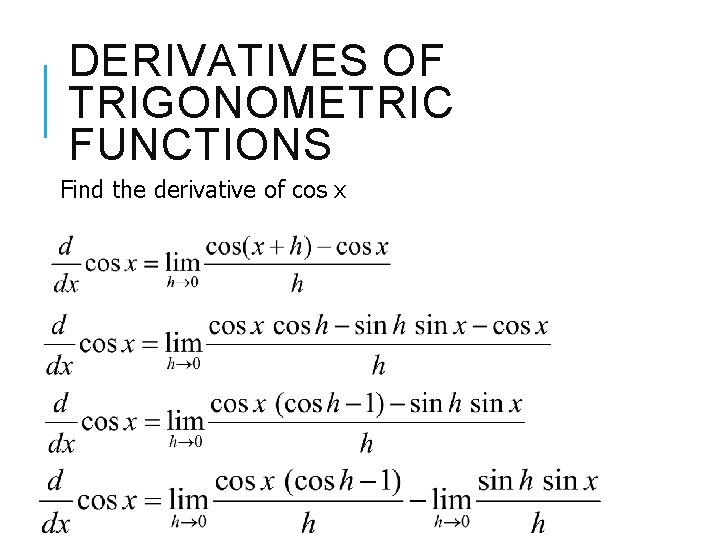





























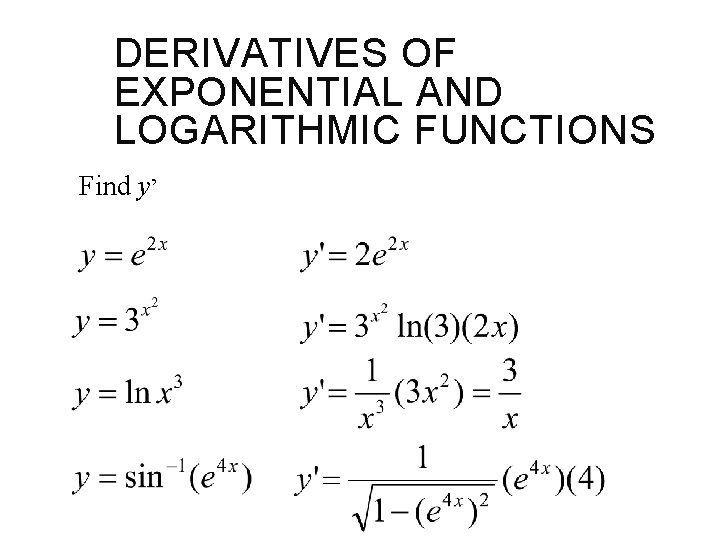

- Slides: 77

DERIVATIVE OF A FUNCTION is called the derivative of We write: “The derivative of f with respect to x is …” There are many ways to write the derivative of at .

DERIVATIVE OF A FUNCTION “f dash x” or “the derivative of f with respect to x” “y prime or dash” “dee why dee ecks” or “the derivative of y with respect to x” “dee eff dee ecks” or “the derivative of f with respect to x” “dee ecks uv eff uv ecks” or “the derivative of f of x”

DERIVATIVE OF A FUNCTION dx does not mean d times x ! dy does not mean d times y !

DERIVATIVE OF A FUNCTION does not mean ! (except when it is convenient to think of it as division. )

DERIVATIVE OF A FUNCTION does not mean times ! (except when it is convenient to treat it that way. )

DERIVATIVE OF A FUNCTION The derivative is the slope of the original function. The derivative is defined at the end points of a function on a closed interval.

DERIVATIVE OF A FUNCTION

DERIVATIVE OF A FUNCTION A function is differentiable if it has a derivative everywhere in its domain. It must be continuous and smooth. Functions on closed intervals must have one-sided derivatives defined at the end points.

DIFFERENTIABILITY To be differentiable, a function must be continuous and smooth. Derivatives will fail to exist at: corner cusp vertical tangent discontinuity

DIFFERENTIABILITY Most of the functions we study in calculus will be differentiable.

DIFFERENTIABILITY If f has a derivative at x = a, then f is continuous at x = a. Since a function must be continuous to have a derivative, if it has a derivative then it is continuous.

DIFFERENTIABILITY Intermediate Value Theorem for Derivatives If a and b are any two points in an interval on which f is differentiable, then and takes on every value between . Between a and b, every value between must take on and .

RULES FOR DIFFERENTIATION If the derivative of a function is its slope, then for a constant function, the derivative must be zero. example: The derivative of a constant is zero.

RULES FOR DIFFERENTIATION We saw that if , This is part of a pattern. examples: power rule .

RULES FOR DIFFERENTIATION Proof:

RULES FOR DIFFERENTIATION constant multiple rule: examples:

RULES FOR DIFFERENTIATION constant multiple rule: sum and difference rules: (Each term is treated separately)

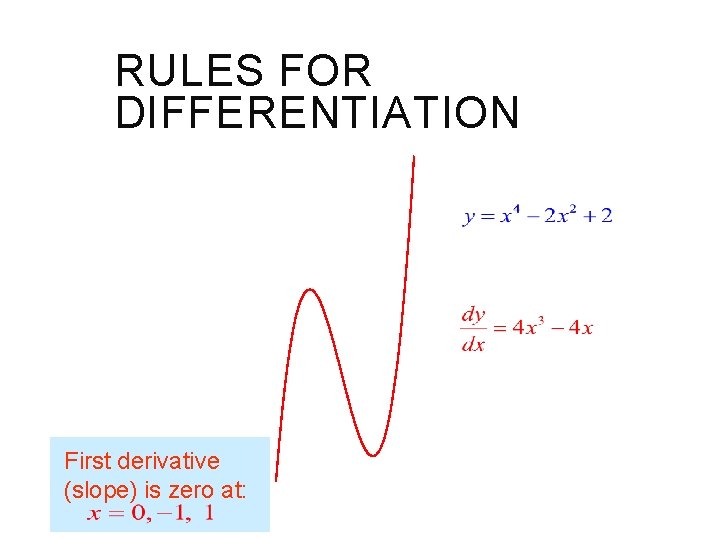
RULES FOR DIFFERENTIATION Find the horizontal tangents of: Horizontal tangents occur when slope = zero. Substituting the x values into the original equation, we get: (The function is even, so we only get two horizontal tangents. )

RULES FOR DIFFERENTIATION

RULES FOR DIFFERENTIATION First derivative (slope) is zero at:

RULES FOR DIFFERENTIATION product rule: Notice that this is not just the product of two derivatives. This is sometimes memorized as:

RULES FOR DIFFERENTIATION product rule: Proof add and subtract u(x+h)v(x) in the denominator

RULES FOR DIFFERENTIATION quotient rule: or

RULES FOR DIFFERENTIATION Higher Order Derivatives: is the first derivative of y with respect to x. is the second derivative. (y double prime) is the third derivative. is the fourth derivative. We will learn later what these higher order derivatives are used for.

RULES FOR DIFFERENTIATION Suppose u and v are functions that are differentiable at x = 3, and that u(3) = 5, u’(3) = -7, v(3) = 1, and v’(3)= 4. Find the following at x = 3 :
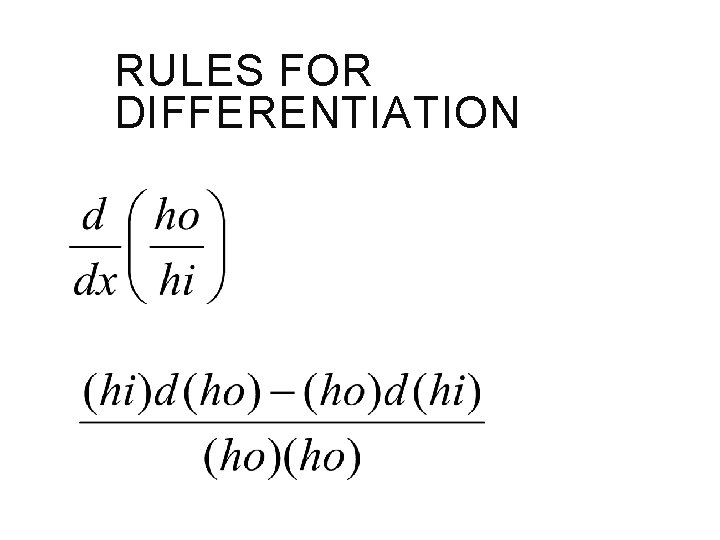
RULES FOR DIFFERENTIATION

RULES FOR DIFFERENTIATION

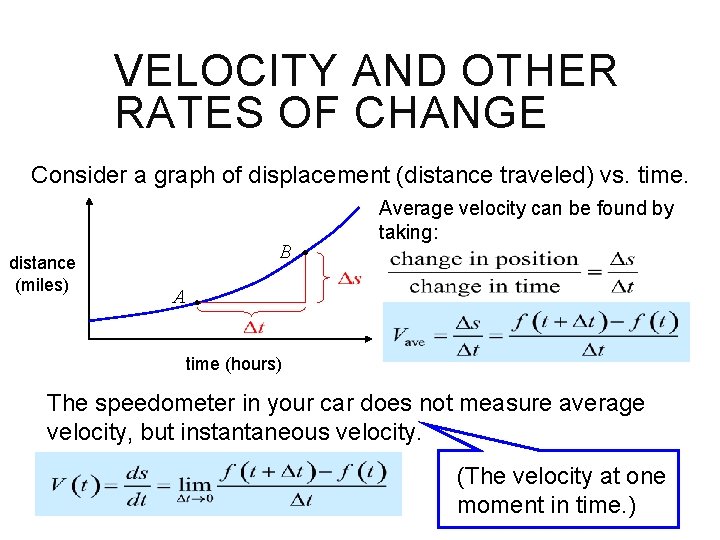
VELOCITY AND OTHER RATES OF CHANGE Consider a graph of displacement (distance traveled) vs. time. distance (miles) B Average velocity can be found by taking: A time (hours) The speedometer in your car does not measure average velocity, but instantaneous velocity. (The velocity at one moment in time. )

VELOCITY AND OTHER RATES OF CHANGE Velocity is the first derivative of position. Acceleration is the second derivative of position.

VELOCITY AND OTHER RATES OF CHANGE Example: Free Fall Equation Speed is the absolute value of velocity. Gravitational Constants:

VELOCITY AND OTHER RATES OF CHANGE Acceleration is the derivative of velocity. example: If distance is in: Velocity would be in: Acceleration would be in:

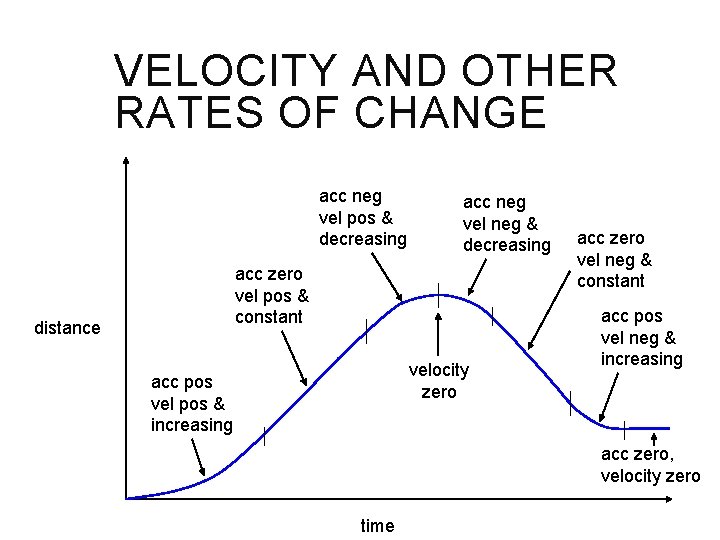
VELOCITY AND OTHER RATES OF CHANGE acc neg vel pos & decreasing acc neg vel neg & decreasing acc zero vel pos & constant distance velocity zero acc pos vel pos & increasing acc zero vel neg & constant acc pos vel neg & increasing acc zero, velocity zero time

VELOCITY AND OTHER RATES OF CHANGE Rates of Change: Average rate of change = Instantaneous rate of change = These definitions are true for any function. ( x does not have to represent time. )

VELOCITY AND OTHER RATES OF CHANGE For a circle: Instantaneous rate of change of the area with respect to the radius. For tree ring growth, if the change in area is constant then dr must get smaller as r gets larger.

VELOCITY AND OTHER RATES OF CHANGE from Economics: Marginal cost is the first derivative of the cost function, and represents an approximation of the cost of producing one more unit.

VELOCITY AND OTHER RATES OF CHANGE Example 13: Suppose it costs: to produce x stoves. If you are currently producing 10 stoves, the 11 th stove will cost approximately: The actual cost is: marginal cost actual cost

VELOCITY AND OTHER RATES OF CHANGE Note that this is not a great approximation – Don’t let that bother you. Marginal cost is a linear approximation of a curved function. For large values it gives a good approximation of the cost of producing the next item.

VELOCITY AND OTHER RATES OF CHANGE

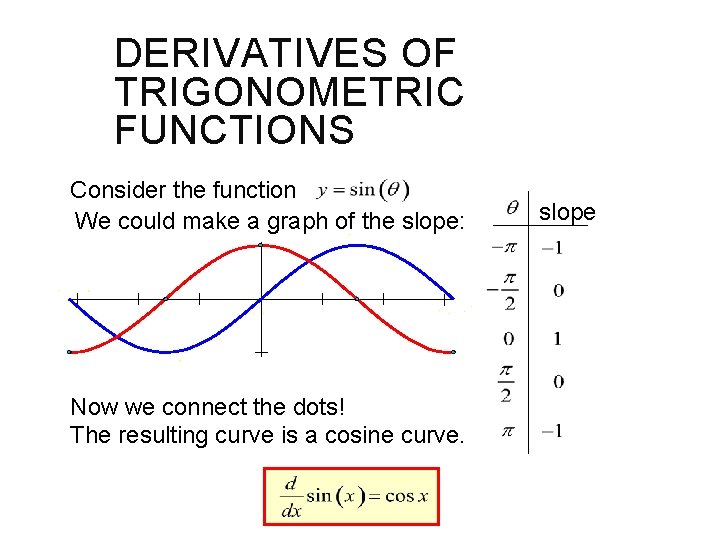
DERIVATIVES OF TRIGONOMETRIC FUNCTIONS Consider the function We could make a graph of the slope: Now we connect the dots! The resulting curve is a cosine curve. slope

DERIVATIVES OF TRIGONOMETRIC FUNCTIONS Proof

DERIVATIVES OF TRIGONOMETRIC FUNCTIONS = 0 =1
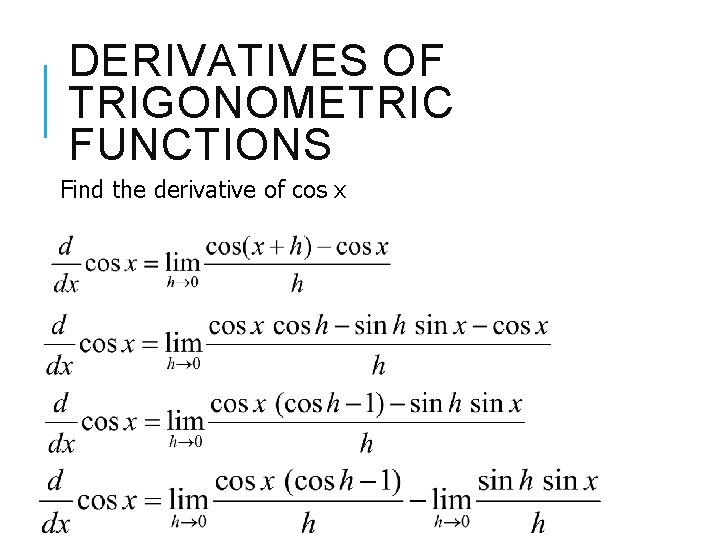
DERIVATIVES OF TRIGONOMETRIC FUNCTIONS Find the derivative of cos x

DERIVATIVES OF TRIGONOMETRIC FUNCTIONS = 0 =1

DERIVATIVES OF TRIGONOMETRIC FUNCTIONS We can find the derivative of tangent x by using the quotient rule.

DERIVATIVES OF TRIGONOMETRIC FUNCTIONS Derivatives of the remaining trig functions can be determined the same way.

DERIVATIVES OF TRIGONOMETRIC FUNCTIONS Jerk A sudden change in acceleration Definition Jerk is the derivative of acceleration. If a body’s position at time t is s(t), the body’s jerk at time t is

DERIVATIVES OF TRIGONOMETRIC FUNCTIONS

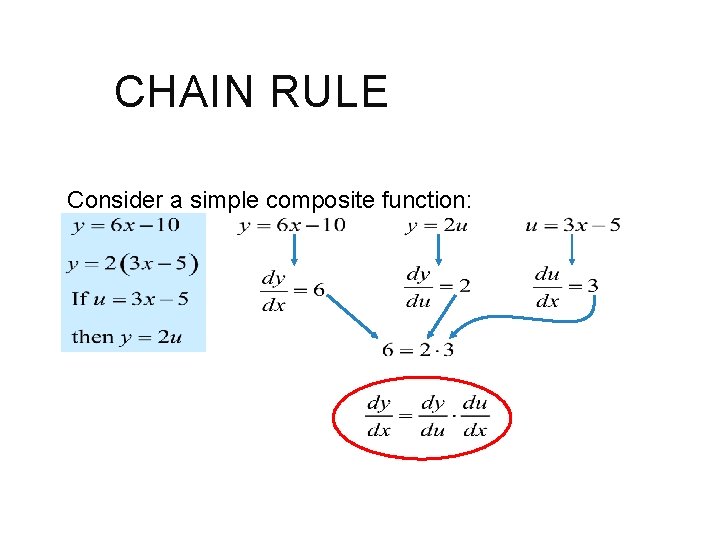
CHAIN RULE Consider a simple composite function:

CHAIN RULE Chain Rule: If then: example: is the composite of and Find: ,

CHAIN RULE

CHAIN RULE Here is a faster way to find the derivative: Differentiate the outside function. . . …then the inside function

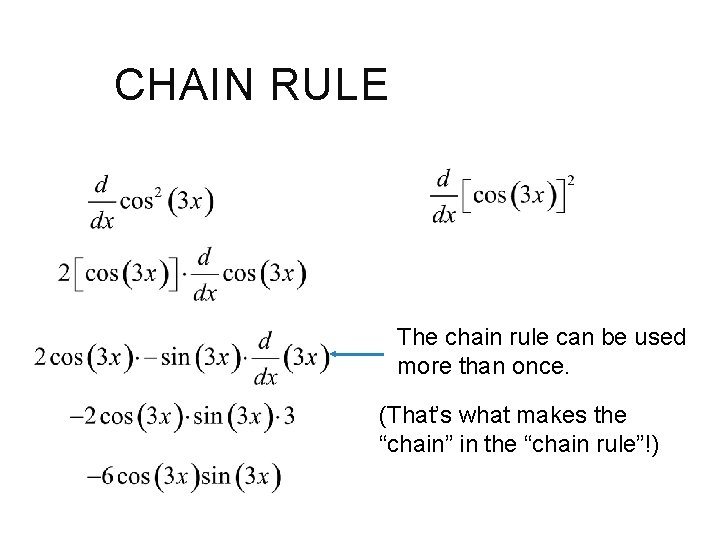
CHAIN RULE The chain rule can be used more than once. (That’s what makes the “chain” in the “chain rule”!)

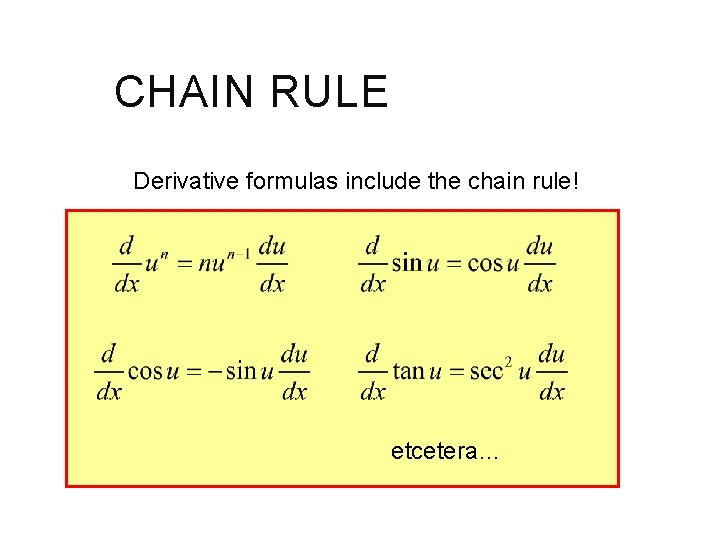
CHAIN RULE Derivative formulas include the chain rule! etcetera…

CHAIN RULE Find

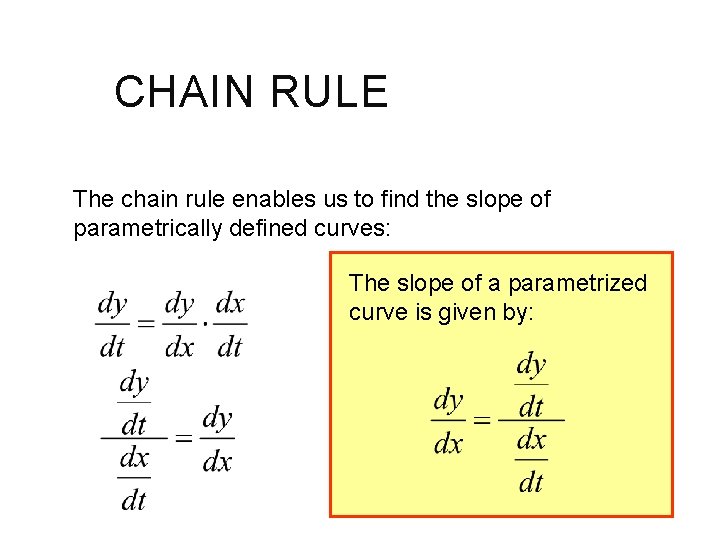
CHAIN RULE The chain rule enables us to find the slope of parametrically defined curves: The slope of a parametrized curve is given by:

CHAIN RULE Example: These are the equations for an ellipse.

IMPLICIT DIFFERENTIATION This is not a function, but it would still be nice to be able to find the slope. Do the same thing to both sides. Note use of chain rule.

IMPLICIT DIFFERENTIATION This can’t be solved for y. This technique is called implicit differentiation. 1 Differentiate both sides w. r. t. x. 2 Solve for .

IMPLICIT DIFFERENTIATION Implicit Differentiation Process 1. 2. 3. 4. Differentiate both sides of the equation with respect to x. Collect the terms with dy/dx on one side of the equation. Factor out dy/dx. Solve for dy/dx.

IMPLICIT DIFFERENTIATION Find the equations of the lines tangent and normal to the curve at Note product rule. .

IMPLICIT DIFFERENTIATION Find the equations of the lines tangent and normal to the curve at tangent: . normal:

IMPLICIT DIFFERENTIATION

IMPLICIT DIFFERENTIATION Find if . Substitute back into the equation.

IMPLICIT DIFFERENTIATION Rational Powers of Differentiable Functions Power Rule for Rational Powers of x If n is any rational number, then

IMPLICIT DIFFERENTIATION Proof: Let p and q be integers with q > 0. Raise both sides to the q power Differentiate with respect to x Solve for dy/dx

IMPLICIT DIFFERENTIATION Substitute for y Remove parenthesis Subtract exponents

DERIVATIVES OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS Look at the graph of The slope at x = 0 appears to be 1. If we assume this to be true, then: definition of derivative

DERIVATIVES OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS Now we attempt to find a general formula for the derivative of using the definition. This is the slope at x = 0, which we have assumed to be 1.


DERIVATIVES OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS is its own derivative! If we incorporate the chain rule: We can now use this formula to find the derivative of

DERIVATIVES OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS Incorporating the chain rule:

DERIVATIVES OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS So far today we have: Now it is relatively easy to find the derivative of .

DERIVATIVES OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS

DERIVATIVES OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS To find the derivative of a common log function, you could just use the change of base rule for logs: The formula for the derivative of a log of any base other than e is:

DERIVATIVES OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS
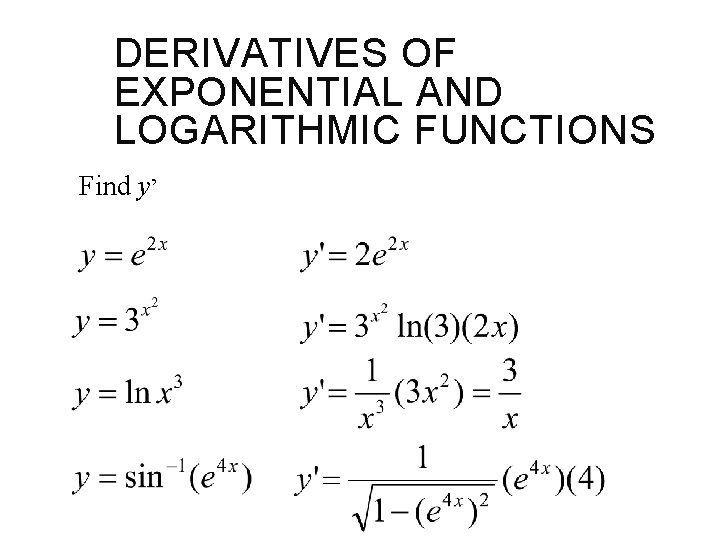
DERIVATIVES OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS Find y’

DERIVATIVES OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS Logarithmic differentiation Used when the variable is in the base and the exponent y = xx ln y = ln xx ln y = x ln x
 The derivative of a function
The derivative of a function Derivative of a function to the slope of the tangent line
Derivative of a function to the slope of the tangent line The chain rule
The chain rule Inverse function
Inverse function Log properties
Log properties How to find stationary points
How to find stationary points Log and exponential derivatives
Log and exponential derivatives Derivative of trigonometry
Derivative of trigonometry First derivative of exponential function
First derivative of exponential function Derivative of sign function
Derivative of sign function Derivative of inverse trig functions
Derivative of inverse trig functions Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể Lp html
Lp html Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Chó sói
Chó sói Tư thế worms-breton
Tư thế worms-breton Chúa sống lại
Chúa sống lại Môn thể thao bắt đầu bằng từ đua
Môn thể thao bắt đầu bằng từ đua Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Cong thức tính động năng
Cong thức tính động năng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Mật thư tọa độ 5x5
Mật thư tọa độ 5x5 101012 bằng
101012 bằng độ dài liên kết
độ dài liên kết Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thể thơ truyền thống
Thể thơ truyền thống Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Một số thể thơ truyền thống
Một số thể thơ truyền thống Cái miệng bé xinh thế chỉ nói điều hay thôi
Cái miệng bé xinh thế chỉ nói điều hay thôi Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Biện pháp chống mỏi cơ
Biện pháp chống mỏi cơ đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ V cc
V cc Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Phối cảnh
Phối cảnh Thẻ vin
Thẻ vin đại từ thay thế
đại từ thay thế điện thế nghỉ
điện thế nghỉ Tư thế ngồi viết
Tư thế ngồi viết Diễn thế sinh thái là
Diễn thế sinh thái là Dot
Dot Bảng số nguyên tố
Bảng số nguyên tố Tư thế ngồi viết
Tư thế ngồi viết Lời thề hippocrates
Lời thề hippocrates Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan ưu thế lai là gì
ưu thế lai là gì Hổ đẻ mỗi lứa mấy con
Hổ đẻ mỗi lứa mấy con Khi nào hổ mẹ dạy hổ con săn mồi
Khi nào hổ mẹ dạy hổ con săn mồi Sơ đồ cơ thể người
Sơ đồ cơ thể người Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Non-updating function module called for updating
Non-updating function module called for updating Why do we study thermodynamics
Why do we study thermodynamics Rational function parent function
Rational function parent function Transforming rational functions
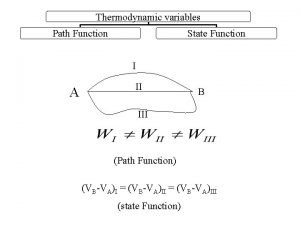
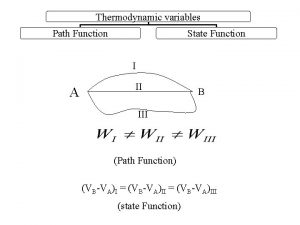
Transforming rational functions Pressure is state function or path function
Pressure is state function or path function Cos parent function table
Cos parent function table Table is linear or nonlinear
Table is linear or nonlinear What is the parent function for exponential functions
What is the parent function for exponential functions Pressure is state function or path function
Pressure is state function or path function 1-6 relations
1-6 relations Rational odd parent function
Rational odd parent function Absolute value of x as a piecewise function
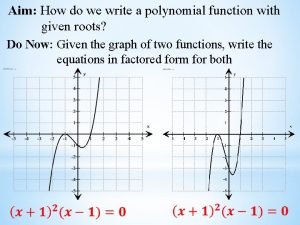
Absolute value of x as a piecewise function Identify polynomial function
Identify polynomial function Rational function forms
Rational function forms How a predicate function become a propositional function?
How a predicate function become a propositional function? Quadratic cubic linear
Quadratic cubic linear What is not a one to one function
What is not a one to one function Composite exponential function
Composite exponential function The inverse of exponential function is a composite function
The inverse of exponential function is a composite function Rumus penerimaan
Rumus penerimaan Polynomial function parent function
Polynomial function parent function State vs path function
State vs path function Power function end behavior model
Power function end behavior model What is function prototype
What is function prototype Grand sauce made from milk and white roux
Grand sauce made from milk and white roux