WORK A little calculus and a little physics








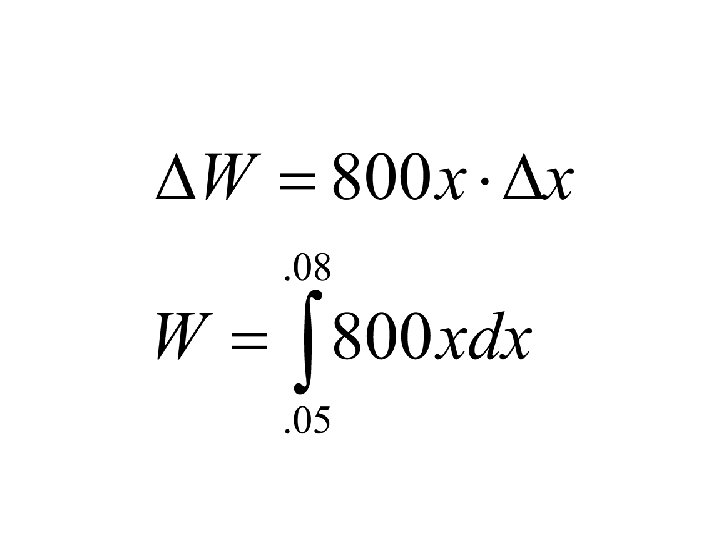



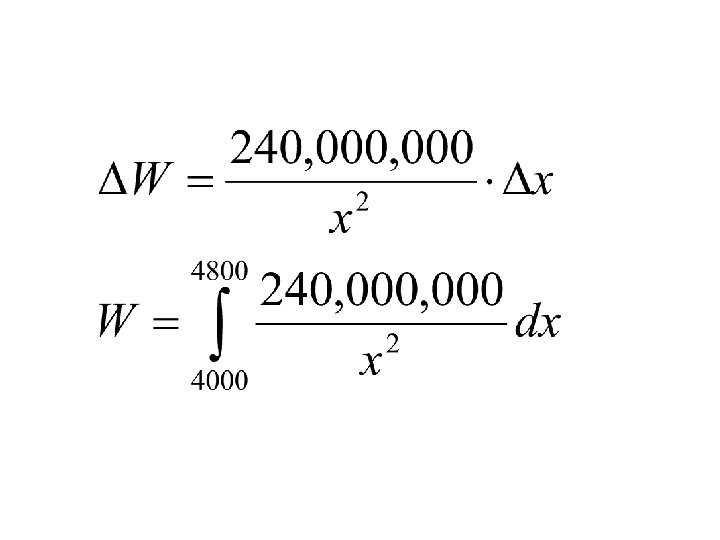









- Slides: 26

WORK A little calculus and a little physics

If dealing with a constant force, W=(F)(d) Units of force include pounds (lbs) and Newtons (N) Units of work include foot-lbs (ft-lbs) and Newton-meters (N-m) also called joules (J)

Easy example: • Find the work done in pushing a car 20 ft while exerting a constant force of 90 lbs.

Answer: • Work = force x distance • Work = 90 lbs x 20 ft • Work = 1800 ft-lbs

What happens when the force is not constant? ? ? Partition the interval from a to b, then calculate the work done in each subinterval. Add ‘em up and take the limit!

A little bit of physics… • Hooke’s law: The force required to maintain a spring x units beyond its natural length is proportional to x. F(x) = kx • Newton’s law of gravitation: where G is a constant, the m’s are the masses of the two objects, and d is the distance between them.

Spring example • A force of 40 N is required to hold a spring that has been stretched from its natural length of 10 cm to 15 cm. How much work is done in stretching the spring from 15 cm to 18 cm?

Use Hooke’s law to find an equation for the force. 40 = k(. 05) k = 800 F(x) = 800 x
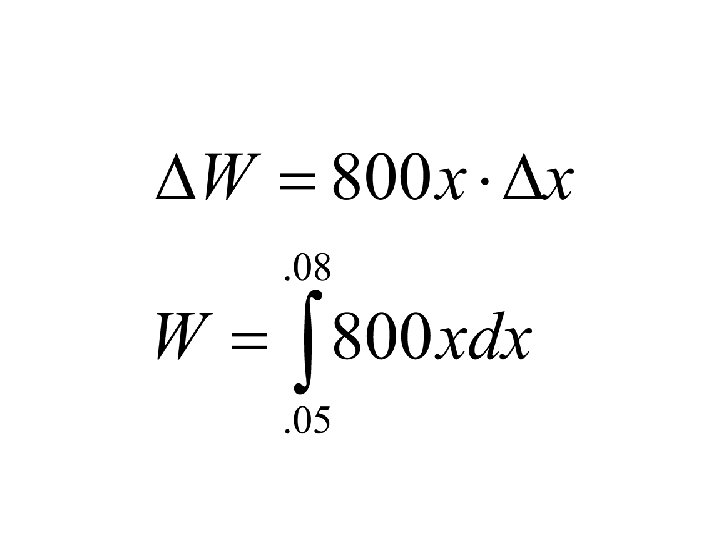

W = 1. 56 N-m or 1. 56 J

Propulsion example A space module weighs 15 tons on the surface of the Earth. How much work is done in propelling the module to a height of 800 miles? (Use 4000 miles as the radius of the Earth. Disregard air resistance and weight of the propellant. )

Use Newton’s Law…
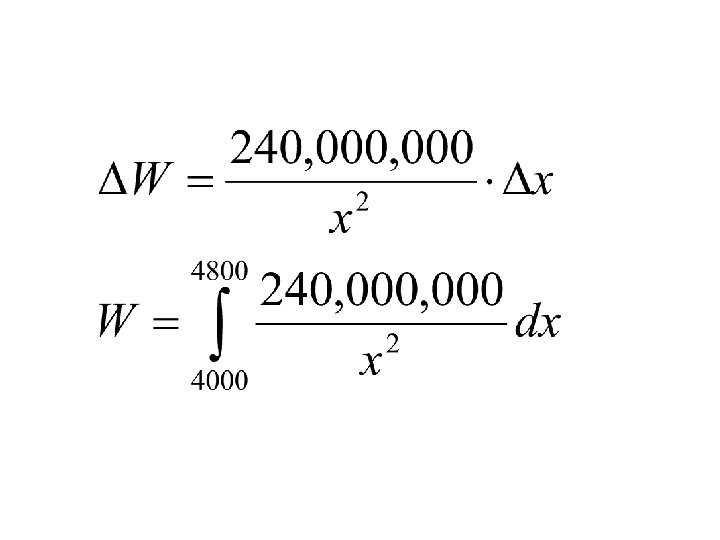

Check your units!!! W = 10000 mile-tons Convert to foot-pounds…

W = 10000 mile-tons Convert to foot-pounds…

ΔW can be found in two ways… • ΔW = F·Δx • ΔW = ΔF·x • Propulsion • Springs • Fluids • Chains • Anything where the weight varies

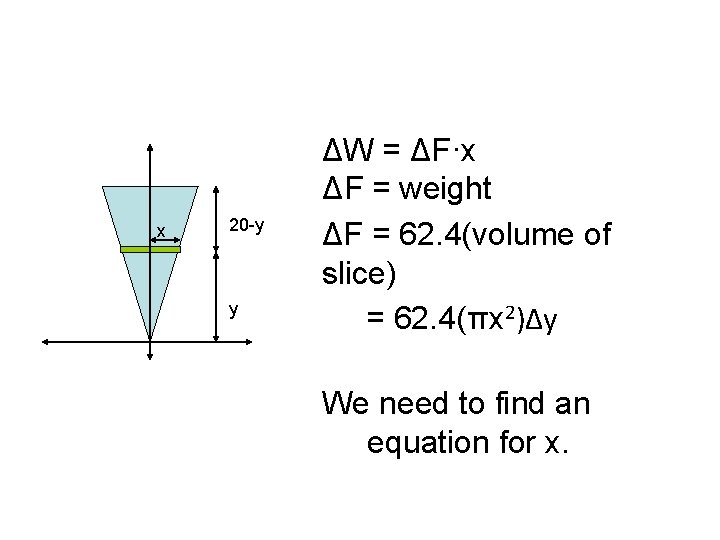
Pumping water example A conical tank with ht 20 feet and base radius 5 ft has its vertex down and axis vertical. If the tank is full of water, find the work done in pumping the water over the top of the tank.

x 20 -y y ΔW = ΔF·x ΔF = weight ΔF = 62. 4(volume of slice) = 62. 4(πx 2)Δy We need to find an equation for x.

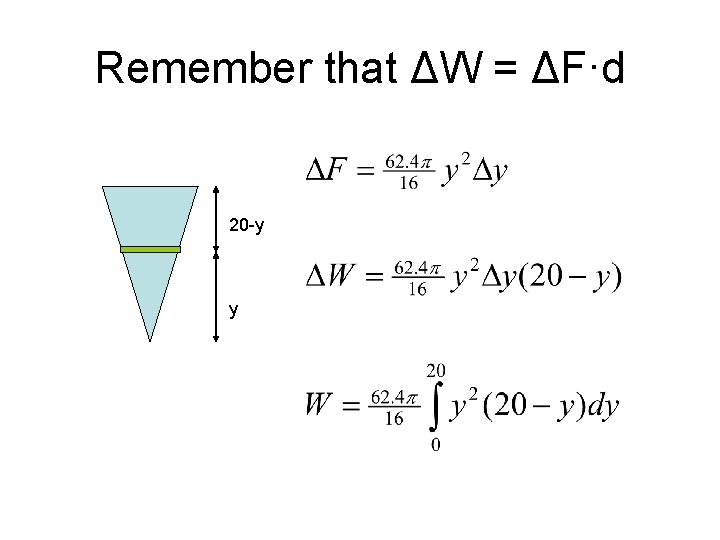
5 20 y = 4 x x = ¼y Volume of highlighted slice = π(¼y)2Δy = πy 2/16 Δy

Remember that ΔW = ΔF·d 20 -y y

Check your units! W = 163, 362. 8 ft-lbs

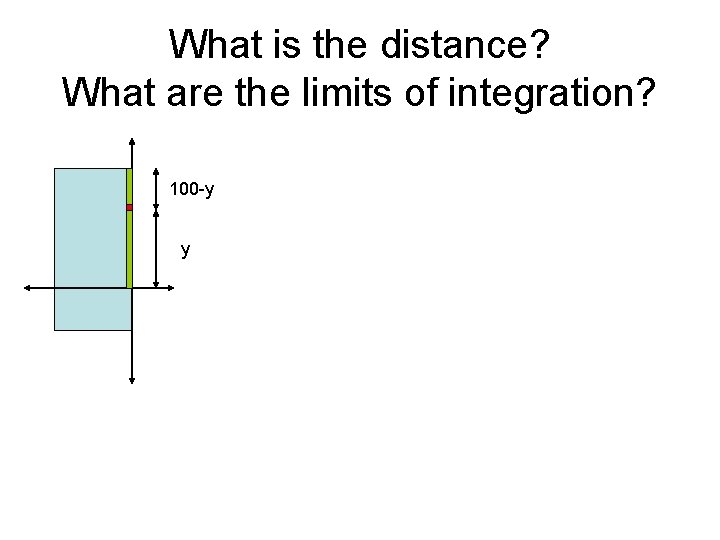
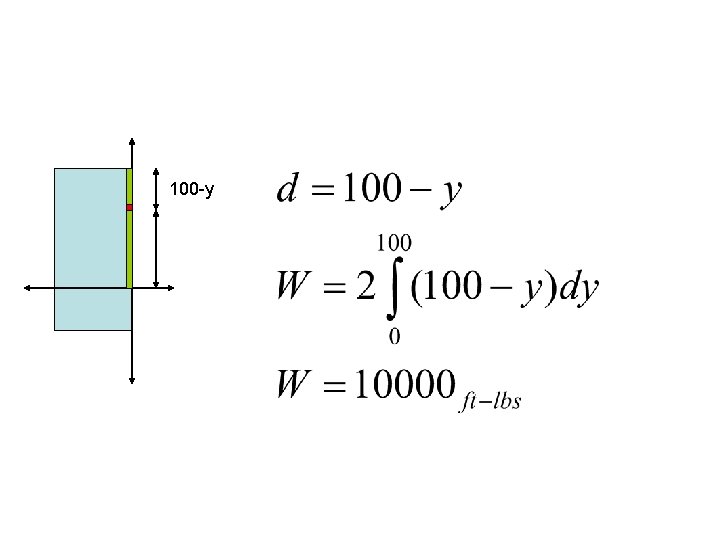
Hanging cable example A 200 pound cable is 100 feet long and hangs vertically from the top of a tall building. How much work is required to lift the cable to the top of the building?

Remember that ΔF = weight

What is the distance? What are the limits of integration? 100 -y y

100 -y

At last, your homework: p 451 # 5, 7, 9, 13, 15, 19, 23, 25, 29, and 31 All are write-ups, due next week. You may use your calculator to integrate. Show all integrals.