VARIGNONS THEOREM What is Varigons Theorem The theorem





- Slides: 6

VARIGNON'S THEOREM

What is Varigon’s Theorem ◦ The theorem states that the torque of a resultant of two concurrent forces about any point is equal to the algebraic sum of the torques of its components about the same point. In other words, "If many concurrent forces are acting on a body, then the algebraic sum of torques of all the forces about a point in the plane of the forces is equal to the torque of their resultant about the same point.

Formal Definition Varigon's theorem states that the sum of the moments produced by any two concurrent forces with respect to a point is equal to the moment produced by the resultant with respect to the same point. This theorem is also known as theorem of moments. Figure shows two concurrent forces F 1 and F 2 and their resultant R. The moment produced by R with respect to a moment center O is R x d. The summation of the moments of F 1 and F 2 with respect to the same moment center O is F 1 d 1 + F 2 d 2. Then as per Varigon's theorem, R d = F 1 d 1 + F 2 d 2

Continue… The theorem initially stated for two concurrent forces, but, it is true for any number of concurrent or coplanar forces. One of the practical applications of theorem is to find the unknown reactions when a system is known to be in equilibrium under the action of a number of forces. Since the resultant is zero for a system in equilibrium we can equate the moment summation of all forces to zero leading to the solution of unknown reactions.

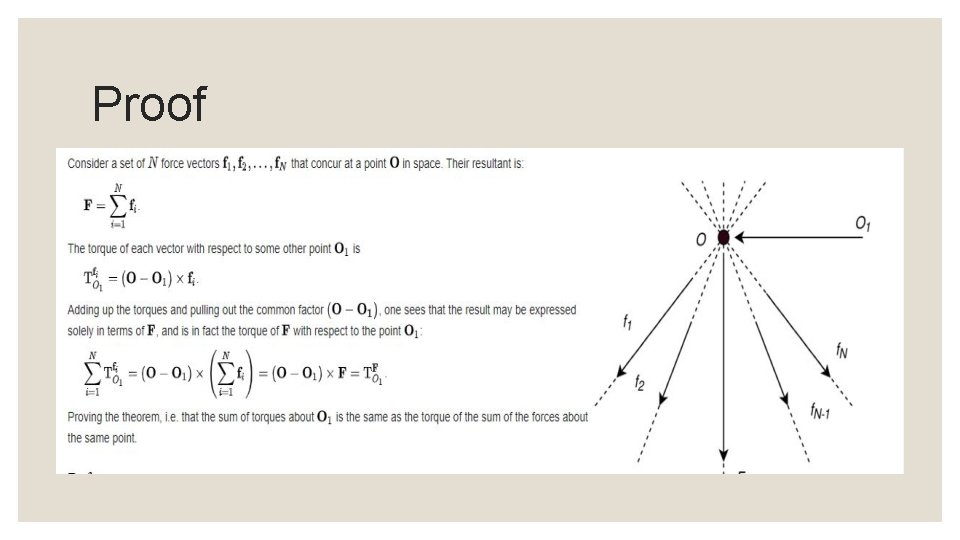
Proof

Applications ◦ The multipole expansion applies to 1/r scalar potentials, examples of which include the electric potential and the gravitational potential. ◦ For these potentials, the expression can be used to approximate the strength of a field produced by a localized distribution of charges (or mass) by calculating the first few moments. ◦ For sufficiently large r, a reasonable approximation can be obtained from just the monopole and dipole moments. Higher fidelity can be achieved by calculating higher order moments. ◦ Extensions of the technique can be used to calculate interaction energies and intermolecular forces. ◦ The technique can also be used to determine the properties of an unknown distribution. ◦ Measurements pertaining to multipole moments may be taken and used to infer properties of the underlying distribution. ◦ This technique applies to small objects such as molecules, but has also been applied to the universe itself, being for example the technique employed by the WMAP and Planck experiments to analyze the cosmic microwave background radiation.