Programming Languages and Compilers CS 421 Elsa L













![Conversion n n 12/5/2020 -conversion: x. exp -- --> y. (exp [y/x]) Provided Conversion n n 12/5/2020 -conversion: x. exp -- --> y. (exp [y/x]) Provided](https://slidetodoc.com/presentation_image_h/ec6ccf885af0dd231ae3a74c420d8abf/image-14.jpg)



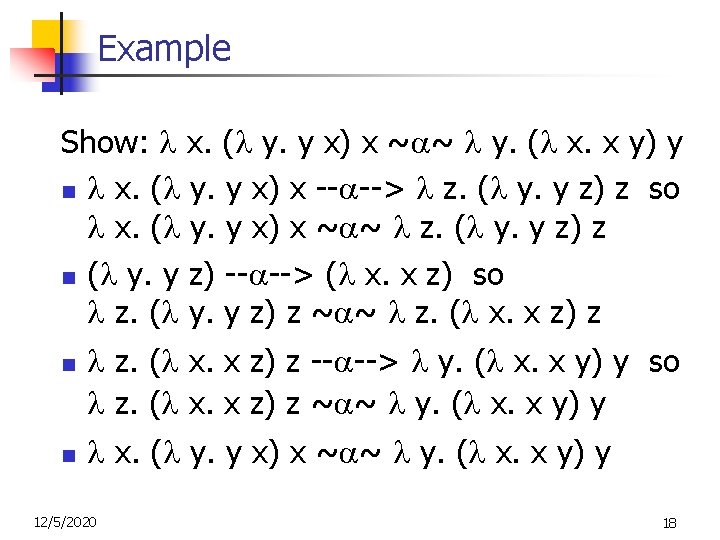

![Substitution n Defined on -equivalence classes of terms P [N / x] means replace Substitution n Defined on -equivalence classes of terms P [N / x] means replace](https://slidetodoc.com/presentation_image_h/ec6ccf885af0dd231ae3a74c420d8abf/image-20.jpg)
![Substitution n x [N / x] = N y [N / x] = y Substitution n x [N / x] = N y [N / x] = y](https://slidetodoc.com/presentation_image_h/ec6ccf885af0dd231ae3a74c420d8abf/image-21.jpg)
![Example ( y. y z) [( x. x y) / z] = ? n Example ( y. y z) [( x. x y) / z] = ? n](https://slidetodoc.com/presentation_image_h/ec6ccf885af0dd231ae3a74c420d8abf/image-22.jpg)

![reduction Rule: ( x. P) N -- --> P [N /x] n n reduction Rule: ( x. P) N -- --> P [N /x] n n](https://slidetodoc.com/presentation_image_h/ec6ccf885af0dd231ae3a74c420d8abf/image-24.jpg)




















- Slides: 44

Programming Languages and Compilers (CS 421) Elsa L Gunter 2112 SC, UIUC http: //www. cs. illinois. edu/class/cs 421/ Based in part on slides by Mattox Beckman, as updated by Vikram Adve and Gul Agha 12/5/2020 1

Lambda Calculus - Motivation n Aim is to capture the essence of functions, function applications, and evaluation calculus is a theory of computation “The Lambda Calculus: Its Syntax and Semantics”. H. P. Barendregt. North Holland, 1984 12/5/2020 2

Lambda Calculus - Motivation n All sequential programs may be viewed as functions from input (initial state and input values) to output (resulting state and output values). -calculus is a mathematical formalism of functions and functional computations Two flavors: typed and untyped 12/5/2020 3

Untyped -Calculus n Only three kinds of expressions: Variables: x, y, z, w, … n Abstraction: x. e n (Function creation, think fun x -> e) n 12/5/2020 Application: e 1 e 2 4

Untyped -Calculus Grammar n Formal BNF Grammar: n <expression> <variable> | <abstraction> | <application> | (<expression>) n <abstraction> <variable>. <expression> n <application> <expression> 12/5/2020 5

Untyped -Calculus Terminology n n n Occurrence: a location of a subterm in a term Variable binding: x. e is a binding of x in e Bound occurrence: all occurrences of x in x. e Free occurrence: one that is not bound Scope of binding: in x. e, all occurrences in e not in a subterm of the form x. e’ (same x) Free variables: all variables having free occurrences in a term 12/5/2020 6

Example n Label occurrences and scope: ( x. y. y ( x. x y) x) x 12/5/2020 7

Example n Label occurrences and scope: ( x. y y. y ( x. x y) x) x 12/5/2020 8

Untyped -Calculus n How do you compute with the -calculus? Roughly speaking, by substitution: n ( x. e 1) e 2 * e 1 [e 2 / x] n n * Modulo all kinds of subtleties to avoid free variable capture 12/5/2020 9

Transition Semantics for -Calculus E --> E’’ E E’ --> E’’ E’ n n Application (version 1 - Lazy Evaluation) ( x. E) E’ --> E[E’/x] Application (version 2 - Eager Evaluation) E’ --> E’’ ( x. E) E’ --> ( x. E) E’’ ( x. E) V --> E[V/x] V - variable or abstraction (value) 12/5/2020 10

How Powerful is the Untyped -Calculus? n The untyped -calculus is Turing Complete n n Can express any sequential computation Problems: n n n 12/5/2020 How to express basic data: booleans, integers, etc? How to express recursion? Constants, if_then_else, etc, are conveniences; can be added as syntactic sugar 11

Typed vs Untyped -Calculus n n The pure -calculus has no notion of type: (f f) is a legal expression Types restrict which applications are valid Types are not syntactic sugar! They disallow some terms Simply typed -calculus is less powerful than the untyped -Calculus: NOT Turing Complete (no recursion) 12/5/2020 12

Uses of -Calculus n n n Typed and untyped -calculus used for theoretical study of sequential programming languages Sequential programming languages are essentially the -calculus, extended with predefined constructs, constants, types, and syntactic sugar Ocaml is close to the -Calculus: fun x -> exp --> x. exp let x = e 1 in e 2 --> ( x. e 2)e 1 12/5/2020 13
![Conversion n n 1252020 conversion x exp y exp yx Provided Conversion n n 12/5/2020 -conversion: x. exp -- --> y. (exp [y/x]) Provided](https://slidetodoc.com/presentation_image_h/ec6ccf885af0dd231ae3a74c420d8abf/image-14.jpg)
Conversion n n 12/5/2020 -conversion: x. exp -- --> y. (exp [y/x]) Provided that 1. y is not free in exp 2. No free occurrence of x in exp becomes bound in exp when replaced by y 14

Conversion Non-Examples y is not free in exp x. x y -- --> y. y y 2. No free occurrence of x becomes bound when replaced by x x. y. x y -- --> y. y y exp[y/x] But x. ( y. y) x -- --> y. ( y. y) y And y. ( y. y) y -- --> x. ( y. y) x 1. 12/5/2020 15

Congruence Let ~ be a relation on lambda terms. ~ is a congruence if n it is an equivalence relation n If e 1 ~ e 2 then n (e e 1) ~ (e e 2) and (e 1 e) ~ (e 2 e) n x. e 1 ~ x. e 2 n 12/5/2020 16

Equivalence n n equivalence is the smallest congruence containing conversion One usually treats -equivalent terms as equal - i. e. use equivalence classes of terms 12/5/2020 17
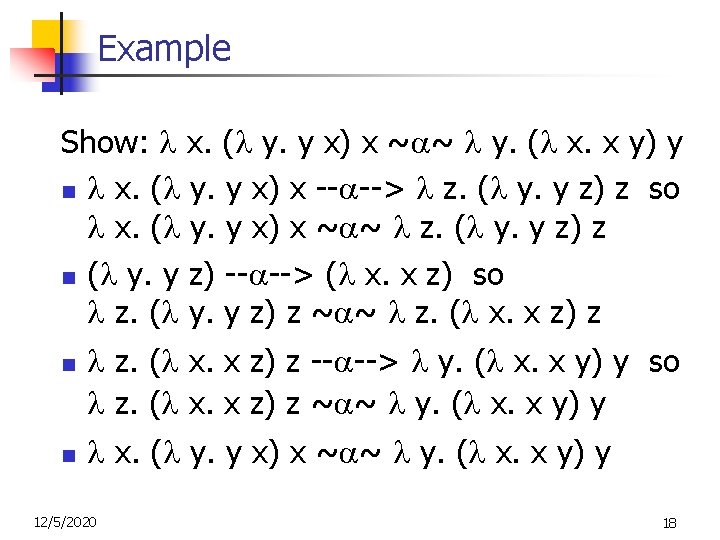
Example Show: x. ( y. y x) x ~ ~ y. ( x. x y) y n x. ( y. y x) x -- --> z. ( y. y z) z so x. ( y. y x) x ~ ~ z. ( y. y z) z n ( y. y z) -- --> ( x. x z) so z. ( y. y z) z ~ ~ z. ( x. x z) z n n z. ( x. x z) z -- --> y. ( x. x y) y so z. ( x. x z) z ~ ~ y. ( x. x y) y x. ( y. y x) x ~ ~ y. ( x. x y) y 12/5/2020 18

(Eta) Reduction n Rule: x. f x -- --> f if x not free in f n Can be useful in each direction Not valid in Ocaml n recall lambda-lifting and side effects n Not equivalent to ( x. f) x --> f (inst of ) n n Example: x. ( y. y) x -- --> y. y 12/5/2020 19
![Substitution n Defined on equivalence classes of terms P N x means replace Substitution n Defined on -equivalence classes of terms P [N / x] means replace](https://slidetodoc.com/presentation_image_h/ec6ccf885af0dd231ae3a74c420d8abf/image-20.jpg)
Substitution n Defined on -equivalence classes of terms P [N / x] means replace every free occurrence of x in P by N Provided that no variable free in P becomes bound in P [N / x] n Rename bound variables in P to avoid capturing free variables of N 12/5/2020 20
![Substitution n x N x N y N x y Substitution n x [N / x] = N y [N / x] = y](https://slidetodoc.com/presentation_image_h/ec6ccf885af0dd231ae3a74c420d8abf/image-21.jpg)
Substitution n x [N / x] = N y [N / x] = y if y x (e 1 e 2) [N / x] = ((e 1 [N / x] ) (e 2 [N / x] )) n ( x. e) [N / x] = ( x. e) n n n ( y. e) [N / x] = y. (e [N / x] ) provided y x and y not free in N n 12/5/2020 Rename y if necessary 21
![Example y y z x x y z n Example ( y. y z) [( x. x y) / z] = ? n](https://slidetodoc.com/presentation_image_h/ec6ccf885af0dd231ae3a74c420d8abf/image-22.jpg)
Example ( y. y z) [( x. x y) / z] = ? n Problems? z in redex in scope of y binding n y free in the residue n n ( y. y z) [( x. x y) / z] -- --> ( w. w z) [( x. x y) / z] = w. w ( x. x y) 12/5/2020 22

Example Only replace free occurrences n ( y. y z ( z. z)) [( x. x) / z] = y. y ( x. x) ( z. z) Not y. y ( x. x) ( z. ( x. x)) n 12/5/2020 23
![reduction Rule x P N P N x n n reduction Rule: ( x. P) N -- --> P [N /x] n n](https://slidetodoc.com/presentation_image_h/ec6ccf885af0dd231ae3a74c420d8abf/image-24.jpg)
reduction Rule: ( x. P) N -- --> P [N /x] n n n Essence of computation in the lambda calculus Usually defined on -equivalence classes of terms 12/5/2020 24


Equivalence n n n equivalence is the smallest congruence containing equivalence and reduction A term is in normal form if no subterm is equivalent to a term that can be reduced Hard fact (Church-Rosser): if e 1 and e 2 are -equivalent and both are normal forms, then they are equivalent 12/5/2020 26

Order of Evaluation n n Not all terms reduce to normal forms Not all reduction strategies will produce a normal form if one exists 12/5/2020 27

Lazy evaluation: n n Always reduce the left-most application in a top-most series of applications (i. e. Do not perform reduction inside an abstraction) Stop when left-most application is not an application of an abstraction to a term 12/5/2020 28

Example 1 n n ( z. ( x. x)) (( y. y y)) Lazy evaluation: Reduce the left-most application: ( z. ( x. x)) (( y. y y)) -- --> ( x. x) 12/5/2020 29

Eager evaluation n (Eagerly) reduce left of top application to an abstraction Then (eagerly) reduce argument Then -reduce the application 12/5/2020 30

Example 1 n n ( z. ( x. x))(( y. y y)) Eager evaluation: Reduce the rator of the top-most application to an abstraction: Done. Reduce the argument: ( z. ( x. x))(( y. y y)) -- --> ( z. ( x. x))(( y. y y))… n 12/5/2020 31

Example 2 n n ( x. x x)(( y. y y) ( z. z)) Lazy evaluation: ( x. x x )(( y. y y) ( z. z)) -- --> 12/5/2020 32

Example 2 n n ( x. x x)(( y. y y) ( z. z)) Lazy evaluation: ( x. x x )(( y. y y) ( z. z)) -- --> 12/5/2020 33

Example 2 n n ( x. x x)(( y. y y) ( z. z)) Lazy evaluation: ( x. x x )(( y. y y) ( z. z)) -- --> (( y. y y ) ( z. z)) 12/5/2020 34

Example 2 n n ( x. x x)(( y. y y) ( z. z)) Lazy evaluation: ( x. x x )(( y. y y) ( z. z)) -- --> (( y. y y ) ( z. z)) (( y. y y ) ( z. z) 12/5/2020 35

Example 2 n ( x. x x)(( y. y y) ( z. z)) n Lazy evaluation: ( x. x x )(( y. y y) ( z. z)) -- --> (( y. y y ) ( z. z)) 12/5/2020 36

Example 2 n ( x. x x)(( y. y y) ( z. z)) n Lazy evaluation: ( x. x x )(( y. y y) ( z. z)) -- --> (( y. y y ) ( z. z)) -- --> (( z. z ) ( z. z))(( y. y y ) ( z. z)) 12/5/2020 37

Example 2 n ( x. x x)(( y. y y) ( z. z)) n Lazy evaluation: ( x. x x )(( y. y y) ( z. z)) -- --> (( y. y y ) ( z. z)) -- --> (( z. z ) ( z. z))(( y. y y ) ( z. z)) 12/5/2020 38

Example 2 n ( x. x x)(( y. y y) ( z. z)) n Lazy evaluation: ( x. x x )(( y. y y) ( z. z)) -- --> (( y. y y ) ( z. z)) -- --> (( z. z ) ( z. z))(( y. y y ) ( z. z)) 12/5/2020 39

Example 2 n ( x. x x)(( y. y y) ( z. z)) n Lazy evaluation: ( x. x x )(( y. y y) ( z. z)) -- --> (( y. y y ) ( z. z)) -- --> (( z. z ) ( z. z))(( y. y y ) ( z. z)) -- --> ( z. z ) (( y. y y ) ( z. z)) 12/5/2020 40

Example 2 n n ( x. x x)(( y. y y) ( z. z)) Lazy evaluation: ( x. x x )(( y. y y) ( z. z)) -- --> (( y. y y ) ( z. z)) -- --> (( z. z ) ( z. z))(( y. y y ) ( z. z)) -- --> ( z. z ) (( y. y y ) ( z. z)) -- --> ( y. y y ) ( z. z) 12/5/2020 41



Example 2 ( x. x x)(( y. y y) ( z. z)) n Eager evaluation: ( x. x x) (( y. y y) ( z. z)) -- --> ( x. x x) (( z. z ) ( z. z)) -- --> ( x. x x) ( z. z) -- --> z. z n 12/5/2020 44