The Relation between Greens theorem and Stokes theorem

The Relation between Green’s theorem and Stokes’ theorem Closed Line integration and Surface (bounded by closed line) integration - The Extension and Special Case -

The Similarity Green’s Theorem Stokes’ Theorem Both relate closed line integrals with surface integrals

The Difference Green’s Theorem ST Stokes’ Theorem (1) cw GT Anti-cw ROTATION Stokes’ theorem is an extension of Green’s theorem (Stokes’ theorem is a higher dimension of Green’s theorem) Stokes’ theorem describe +ve and –ve surface orientation

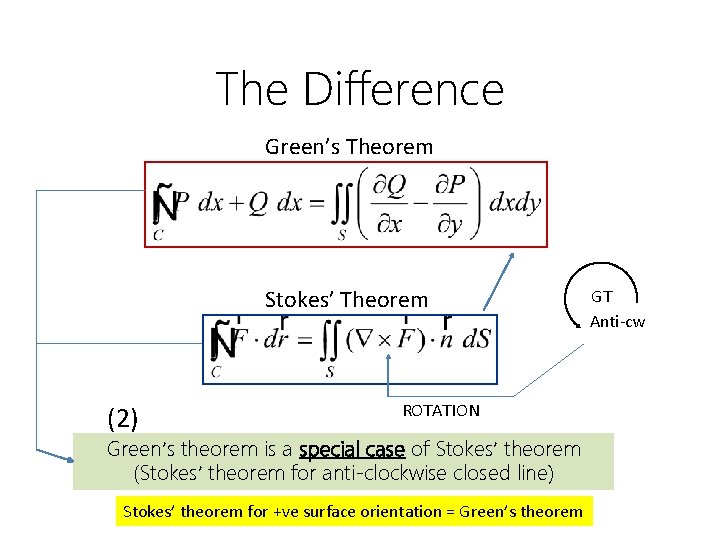
The Difference Green’s Theorem Stokes’ Theorem (2) ROTATION Green’s theorem is a special case of Stokes’ theorem (Stokes’ theorem for anti-clockwise closed line) Stokes’ theorem for +ve surface orientation = Green’s theorem GT Anti-cw

Special case of Stokes’ theorem (Mathematical derivative from Stokes’ theorem to formularize Green’s theorem) z Unit normal vector for positive oriented surface: Let closed line curve C and surface S (bounded by closed line) in x-y plane Closed line in anti-clockwise direction. Choose any two point: 0 x Q P y Vector field refer to P and Q: Vector in x-y plane only

Special case of Stokes’ theorem (Mathematical derivative from Stokes’ theorem to formularize Green’s theorem) From Stokes’ theorem formula: For closed line integration: …………………(1)

Special case of Stokes’ theorem (Mathematical derivative from Stokes’ theorem to formularize Green’s theorem) From Stokes’ theorem formula: For surface integration: P and Q as a function of x and y =0 =0

Special case of Stokes’ theorem (Mathematical derivative from Stokes’ theorem to formularize Green’s theorem) Then, …………………(2)

Special case of Stokes’ theorem (Mathematical derivative from Stokes’ theorem to formularize Green’s theorem) Thus, Eq. (1) = Eq. (2) gives Green’s Theorem If we consider for clockwise direction of closed line, then we have surface in negative orientation, where , thus the relation gives: