The Fundamental Theorem of Calculus Weve learned two






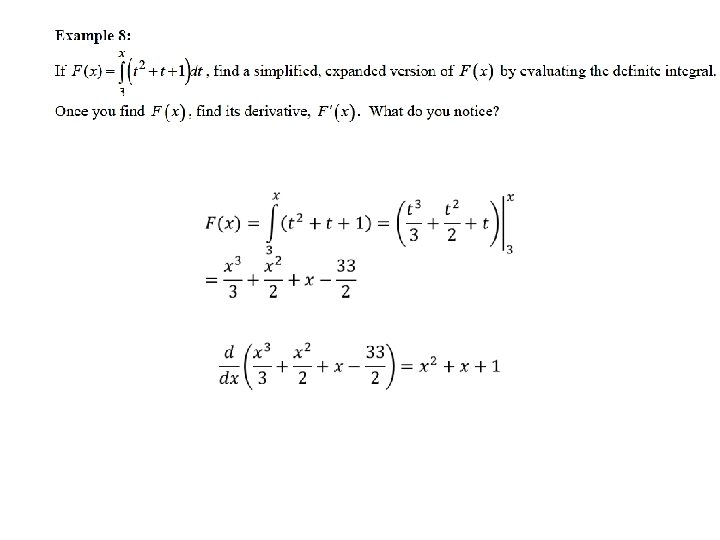





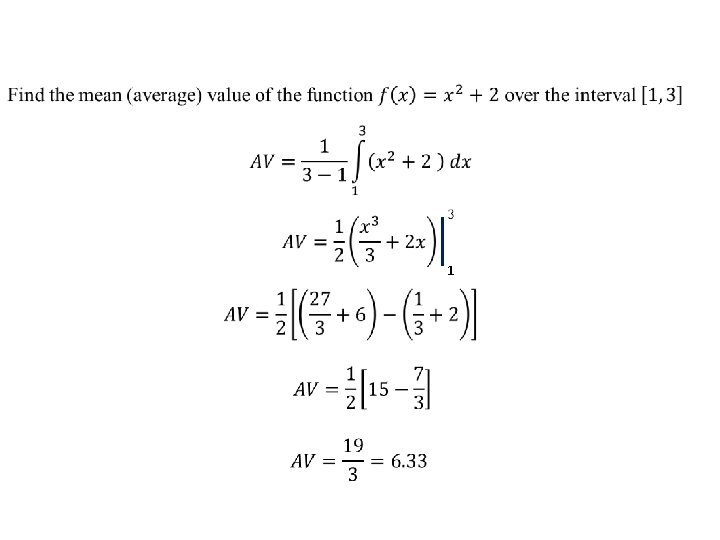



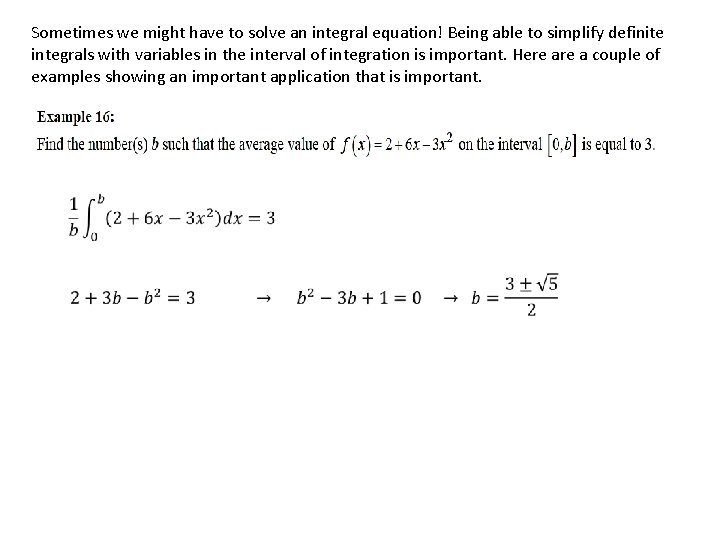



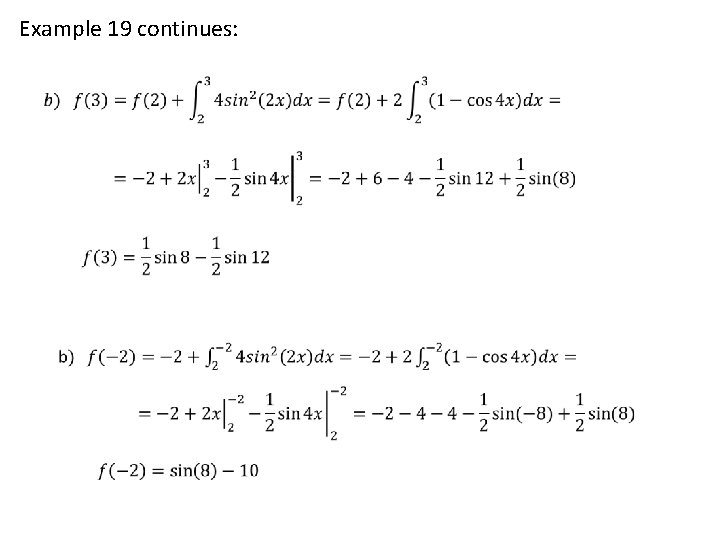


- Slides: 29

The Fundamental Theorem of Calculus We’ve learned two different branches of calculus so far: differentiation and integration. Finding slopes of tangent lines and finding areas under curves seem unrelated, but in fact, they are very closely related. It was Isaac Newton’s teacher at Cambridge University, a man name Isaac Barrow (1630 – 1677), who discovered that these two processes are actually inverse operations of each other in much the same way division and multiplication are. It was Newton and Leibniz who exploited this idea and developed the calculus into it current form. Theorem Barrow discovered that states this inverse relation between differentiation and integration is called The Fundamental Theorem of Calculus.

Fundamental Theorem of Calculus 1 (FTo. C 1) The integral gives the NET change Fundamental Theorem of Calculus 2 (FTo. C 2)

FTo. C 1 bridges the antiderivative concept with the area problem. This result, while taught early in elementary calculus courses, is actually a very deep result connecting the purely algebraic indefinite integral and the purely analytic (or geometric) definite integral. To evaluate an integral, take the antiderivatives and subtract. It can be proved and the proof can be found elsewhere (WEB) It is a “shortcut” rule for integration: an easier way (from Riemann sums and other methods) to calculate definite integrals.






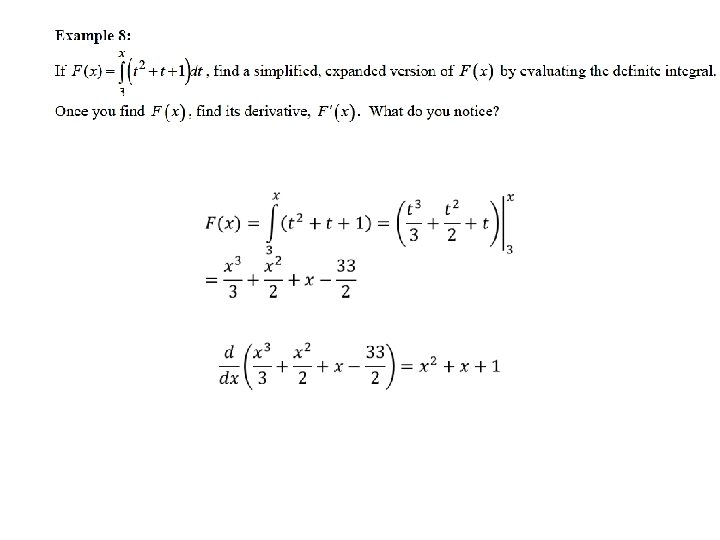

Directly: Or, longer way: Lower limit of integration is a constant.


What if upper limit is g(x) not x itself? Or upper limit is constant and lower limit is x? The upper limit of integration does not match the derivative, but we could use the chain rule. = = = The lower limit of integration is not a constant, but the upper limit is. = = We can change the sign of the integral and reverse the limits.

FTo. C 2, the most general form

Example 10: Evaluate the following using the FTOC 2, then if feeling bored verify by doing in the Loooong way.

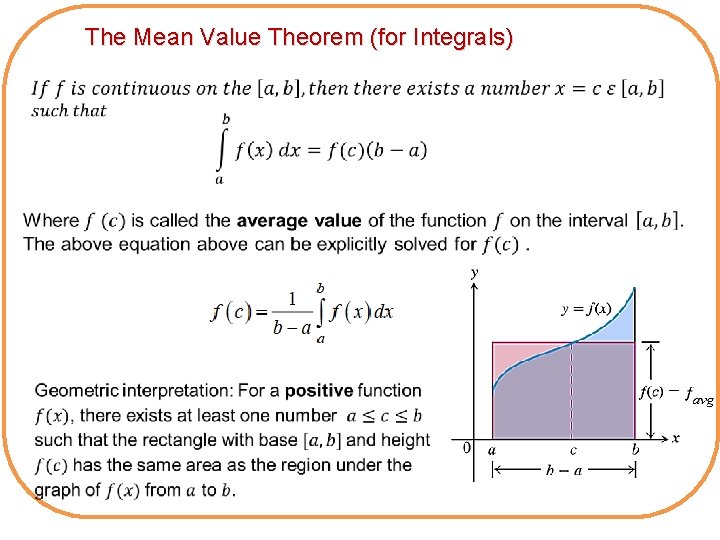
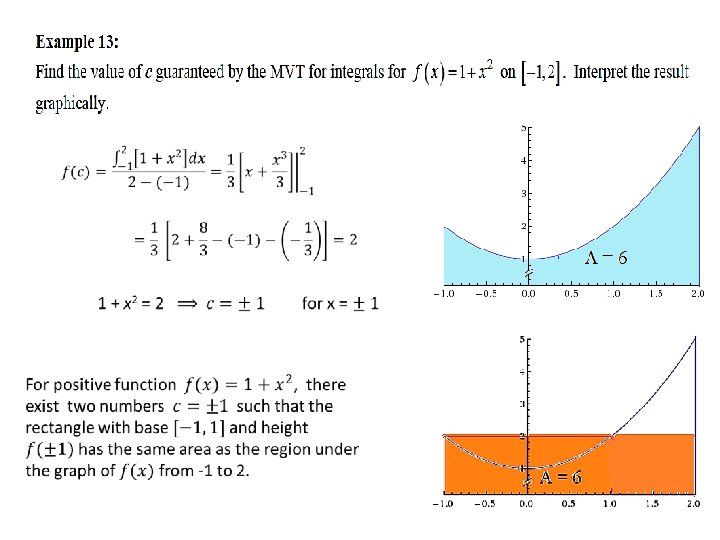
The Mean Value Theorem (for Integrals)
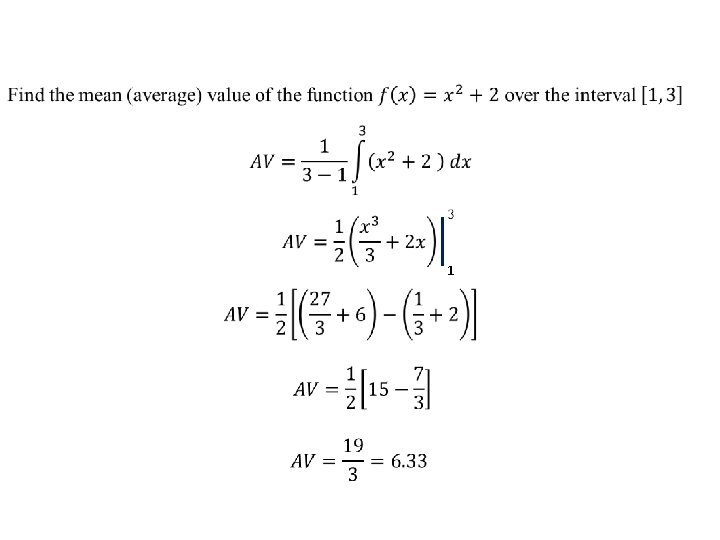
1



The average rate of change of a car’s position over an interval is represented graphically as the slope of the secant line to the graph position/time over the interval. Average value of velocity over the same interval is:

Area trapezoidal approximation is more accurate that LRAM (basically arithmetic mean)
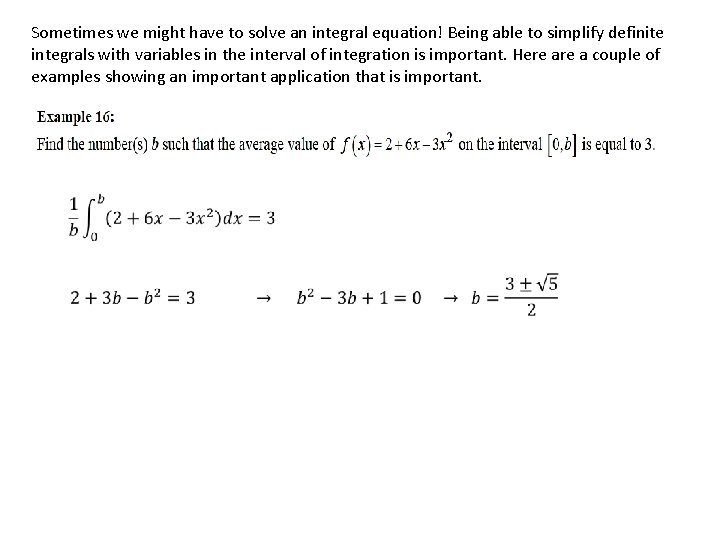
Sometimes we might have to solve an integral equation! Being able to simplify definite integrals with variables in the interval of integration is important. Here a couple of examples showing an important application that is important.



In the previous example, the first method relied heavily upon our ability to find the antiderivative of the integrand. This is not always easy, possible, or prudent! Being able to express a particular value of a particular solution to a derivative as a definite integral is of paramount importance, especially when we don’t know how to find a general antiderivative. (calculator can do easily definite integrals – see problem 20) Hard Facts To Refute: A. Where you are at any given time is a function of 1) where you started and 2) where you’ve gone from your starting point (displacement). B. What you have at any given moment is a function of 1) what you started with plus 2) what you’ve accumulated since then. When you accumulate at a variable rate, you can to use the definite integral to find your net accumulation. Important Idea of Accumulation**************(* means VERY IMPORTANT) What one has now = What one started with + What one has accumulated since one started. This can be expressed mathematically as

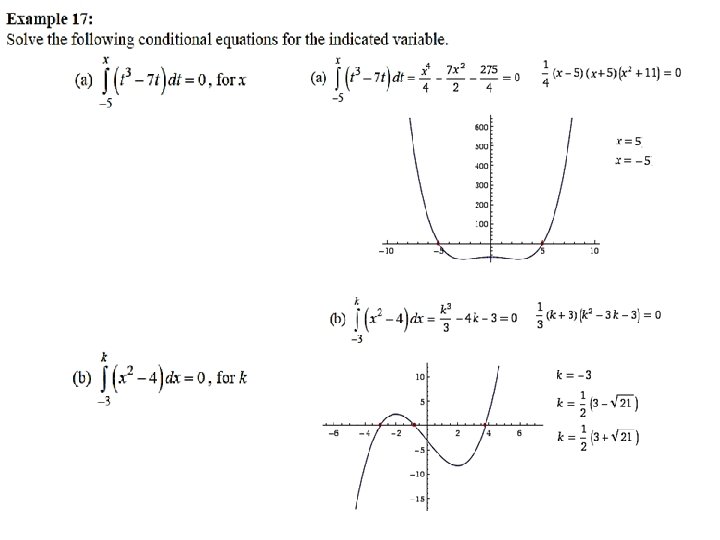
Example 19: (a) and integral equation for f(x) (b) f(3) (c) f(-2)
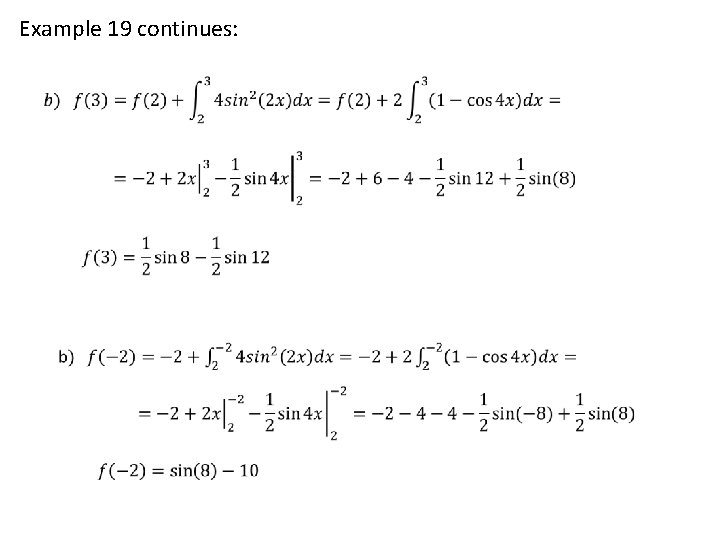
Example 19 continues:


 The fundamental theorem of calculus
The fundamental theorem of calculus Fundamental theorem
Fundamental theorem Calculus
Calculus Fundamental theorem.of calculus
Fundamental theorem.of calculus Fundamental theorem of vector calculus
Fundamental theorem of vector calculus Demand paging in virtual memory
Demand paging in virtual memory Weve a
Weve a Weve been lied to
Weve been lied to Weve got the beat
Weve got the beat The lights from the parlour and kitchen shone out
The lights from the parlour and kitchen shone out Stock theorem
Stock theorem Theorem 4 calculus
Theorem 4 calculus Fundamental theorem of algebra
Fundamental theorem of algebra Fundamental theorem of statistics
Fundamental theorem of statistics Rational root theorem
Rational root theorem Fundamental theorem of algebra
Fundamental theorem of algebra 5-6 the fundamental theorem of algebra
5-6 the fundamental theorem of algebra Fundamental theorem of algebra example
Fundamental theorem of algebra example Complex zeros and the fundamental theorem of algebra
Complex zeros and the fundamental theorem of algebra What is abelian group
What is abelian group Fundamental theorem of counting
Fundamental theorem of counting Definition of health management information system
Definition of health management information system State fundamental theorem of arithmetic
State fundamental theorem of arithmetic Poker kryterialny
Poker kryterialny Calculus examples
Calculus examples Fundamental theorem of asset pricing proof
Fundamental theorem of asset pricing proof Two fundamental business strategies are
Two fundamental business strategies are Cost focus and differentiation focus
Cost focus and differentiation focus Factor theorem long division
Factor theorem long division Polynomial remainder theorem
Polynomial remainder theorem