Relational Calculus Introduction n n The Relational Calculus












![SQL -- Complete Format select [ distinct ] target_list from tuple_variable_list [ where qualification SQL -- Complete Format select [ distinct ] target_list from tuple_variable_list [ where qualification](https://slidetodoc.com/presentation_image/18e606e3a0a34d6d87a82b0443f88b31/image-14.jpg)





























- Slides: 43


Relational Calculus: Introduction n n The Relational Calculus (RC) is a non-procedural, formal language based on first-order predicate calculus Queries in RC specify WHAT is to be retrieved (declarative) while the system takes care of HOW Most commercial relational languages are based on relational calculus (QUEL, QBE, and SQL). Such languages emphasize ease and convenience of use. In terms of expressiveness, RELATIONAL ALGEBRA and RELATIONAL CALCULUS are identical. YV - Relational Calculus, SQL, QBE 155

Relational Calculus: Introduction (2) n n The Relational Calculus uses the notion of VARIABLE There are two flavors of the language: – tuple calculus variables refer to tuples from a specified relation e. g. , t is a tuple variable referring to a tuple of r(R) – domain calculus variables refer to individual values from a specified domain e. g. , d is a domain variable referring to the value which a tuple in r(R) has for attribute A (from domain D) YV - Relational Calculus, SQL, QBE 156

Tuple Calculus n n A TUPLE CALCULUS EXPRESSION defines a new relation in terms of existing (base) relations. An expression is constructed from the following elements: (1) tuple variables (e. g. , t, v, w, t 1, t 2, t 3, . . . tn ), which are defined to range over a specified relation instance r(R) Tuple variables may be restricted, where, t. A, with A an attribute of R, denotes the A-component of the value of t Example: t. Name (2) conditions of the form x operator y, where -- x, y are restricted tuple variables or constant values -- operator Î { =, ¹, <, >, £, ³ } Examples: t. Name = ‘mary’, t. City ¹ v. City YV - Relational Calculus, SQL, QBE 157

Tuple Calculus Expressions (3) Well-Formed Formulas (WFFs), defined as: t a condition is a WFF t if f is a WFF, so is (f) and Ø(f) (where Ø is the logical NOT) t if f and g are WFFs, so are (f & g) and (f | g) (where &, |, are the logical AND, OR respectively) t if f is a WFF with free variable t, so are $t(f), "t(f) (where $, " are the existential and universal quantifiers) A tuple variable t is said to be bound in a formula f if it is one of the quantified variables in f. Otherwise, t is free in f. Example: t is free in f 1 : (t. City = ‘london’) and is bound in f 2 : ("t ) (t. DNumber = v. Dno), while v is free in f 2 YV - Relational Calculus, SQL, QBE 158

Tuple Calculus Expressions n Examples of WFFs – – – – n t. City = v. City (t. City = v. City) Ø (t. City = v. City) (t. City ¹ v. City) (t. City = v. City) & (w. City = london) $t (t. City = v. City) "t (t. City = athens) if f is a WFF, then a tuple calculus expression is any expression of the form: { ti. Aj | ti Î r(Rk) AND f } where Rk are relation schemes and Aj are attributes in Rk YV - Relational Calculus, SQL, QBE 159

Calculus Query Examples n Recall the sailors-boats database SAILORS (Sid, SName, Rating) BOATS (Bid, BName, Color) RESERVE (Sid, Bid, Date) n QUERY 1: Find the names of sailors whose id is greater than 10 and have rating ‘a’ RANGE of t is SAILORS t. SName where & (t. Sid > 10) & (t. Rating = ‘a’) This is an equivalent form of the pure RC query: { t. SName | t Î r(SAILORS) & ((t. Sid > 10) & (t. Rating = ‘a’)) } YV - Relational Calculus, SQL, QBE 160

Calculus Query Examples (2) n QUERY 2: Find the names and ratings of sailors who have reserved boat number 3 RANGE of t is SAILORS RANGE of v is RESERVE t. SName, t. Rating where $v ( (t. Sid = v. Sid) & (v. Bid = 3) ) n QUERY 3: Find the names sailors who have not reserved boat number 3 RANGE of t is SAILORS RANGE of v is RESERVE t. SName where Ø ( $v ( (t. Sid = v. Sid) & (v. Bid = 3) ) ) YV - Relational Calculus, SQL, QBE 161

SQL - Introduction n n SQL (Structured Query Language) has become the “standard” in query languages. It was first used in IBM’s prototype , called SYSTEM-R, developed at San Jose in the mid-seventies. SQL has gone over many evaluations. There are 4 basic commands: – – n select insert update delete (not to be confused with SELECTION in algebra) The result of any query on relations is again a relation YV - Relational Calculus, SQL, QBE 162

SQL - Informal Definition n Assume the EMPLOYEE relation and the following query: “Find the names of employees who earn more than 30000” This is expressed in SQL as: select e. Name from EMPLOYEE e where (e. Salary > 30000) – e is a tuple variable defined to range over the relation EMPLOYEE (in the from clause) – e. Name, as a restricted tuple variable, specifies the value of e in attribute Name, and is the target list (specifies in the select clause the projections of columns) – (e. Salary > 30000) is the qualification (specifies in the where clause all selections and joins) YV - Relational Calculus, SQL, QBE 163

SQL -- Formal Definition n A selection clause is a comparison between a restricted tuple variable x and a constant c of the form : x operator c where operator Î { =, ¹, <, >, £, ³ } Example: n t. Name = ‘mary’, t. Salary > 30000 A join clause is a comparison between two restricted tuple variables x and y of the form x operator y where x, y belong to different relations and operator Î { =, ¹, <, >, £, ³ } Example: YV - Relational Calculus, SQL, QBE t. Name = v. EName 164

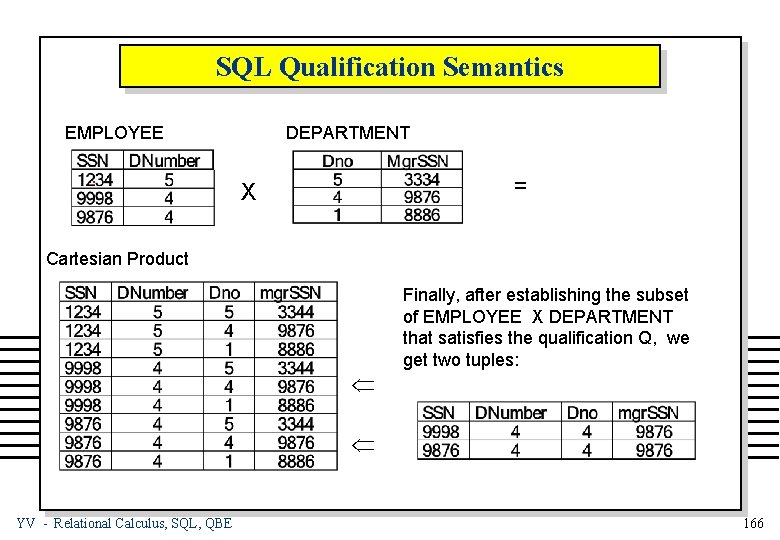
SQL -- Formal Definition (2) n A qualification is a Boolean combination (i. e. , with logical and, or, not) of selection and join clauses. ) Example: n (t. Name = v. EName) and (t. Salary > 30000) QUALIFICATION SEMANTICS A qualification Q describes the subset of the Cartesian product of the ranges of its tuple variables that satisfy Q Example: Consider relations: EMPLOYEE(SSN, DNumber), and DEPARTMENT(Dno, mgr. SSN), with e and d tuple variables Q = (e. DNumber = d. Dno) and (d. mgr. SSN = 9876) Semantics of Q: The set of e, d pairs that satisfy Q YV - Relational Calculus, SQL, QBE 165

SQL Qualification Semantics EMPLOYEE . DEPARTMENT = X Cartesian Product Ü Finally, after establishing the subset of EMPLOYEE X DEPARTMENT that satisfies the qualification Q, we get two tuples: Ü YV - Relational Calculus, SQL, QBE 166
![SQL Complete Format select distinct targetlist from tuplevariablelist where qualification SQL -- Complete Format select [ distinct ] target_list from tuple_variable_list [ where qualification](https://slidetodoc.com/presentation_image/18e606e3a0a34d6d87a82b0443f88b31/image-14.jpg)
SQL -- Complete Format select [ distinct ] target_list from tuple_variable_list [ where qualification ] [ group by grouping_attributes ] [ having group_condition ] [ order by target_list_subset ] – A query is evaluated by first applying the WHERE clause, then GROUP-BY and HAVING (all optional), and finally the SELECT clause (target list) - ordering the resulting tuples if required in the ORDER BY clause (also optional). YV - Relational Calculus, SQL, QBE 167

SQL: Sailor Examples n Consider again the Sailors-Boats database: SAILORS (Sid, SName, Rating) BOATS (Bid, BName, Color) RESERVE (Sid, Bid, Date) n SQUERY 1: Find the names of sailors who have reserved boat number 2 select from where YV - Relational Calculus, SQL, QBE s. SName SAILORS s, RESERVE r s. Sid = r. Sid and r. Bid = 2 168

SQL Sailor Examples (2) n SQUERY 2: Find the names of sailors who have reserved a red boat select from where n s. SName SAILORS s, BOATS b, RESERVE r s. Sid = r. Sid and r. Bid = b. Bid and b. Color = “red” SQUERY 3: Find the colors of the boats reserved by eleni select from where b. Color SAILORS s, BOATS b, RESERVE r s. Sid = r. Sid and r. Bid =b. Bid and s. SName= “eleni” YV - Relational Calculus, SQL, QBE 169

SQL Sailor Examples (3) n SQUERY 4: Find the names of the sailors who have reserved at least one boat select from where n s. SName SAILORS s, RESERVE r s. Sid = r. Sid SQUERY 5: Find the names of sailors who have reserved a red or a green boat select from where YV - Relational Calculus, SQL, QBE s. SName SAILORS s, BOATS b, RESERVE r s. Sid = r. Sid and r. Bid = b. Bid and (b. Color = “red” or b. Color = “green”) 170

SQL Sailor Examples (4) n SQUERY 6: Find the names of sailors who have reserved both a red and a green boat select from where YV - Relational Calculus, SQL, QBE s. SName SAILORS s, BOATS b 1, RESERVE r 1, BOATS b 2, RESERVE r 2 s. Sid = r 1. Sid and r 1. Bid = b 1. Bid and b 1. Color = “red” and s. Sid = r 2. Sid and r 2. Bid = b 2. Bid and b 2. Color = “green” 171

SQL Elaboration: Examples from the COMPANY database EMPLOYEE ( SSN, Name, Birth. Date, Address, Sex, Salary, Sup. SSN, DNumber) DEPARTMENT ( DNumber, DName, Mgr. SSN, Mgr. Start. Date) PROJECT ( PNumber, PName, Location, DNumber) DEPT_LOCATION ( DNumber, DLocation) WORKS_ON ( SSN, PNumber, Hours. PW) DEPENDENT ( SSN, Depend. Name, Sex, Birth. Date, Relationship) YV - Relational Calculus, SQL, QBE 172

SQL: Target List Examples (1) n TARGET LISTS: Each item in a target list can be as general as: attribute_name = expression where expression is any arithmetic or string expression over restricted tuple variables and constants (also builtins and aggregates. ) n CQUERY 1: List, increased by 10000 the salary of employees who have worked on two different projects more than 25 hours select from where YV - Relational Calculus, SQL, QBE e. Name, Salary = e. Salary + 10000 EMPLOYEE e, WORKS_ON w 1, WORKS_ON w 2 e. SSN = w 1. SSN and e. SSN = w 2. SSN and w 1. Hours. PW > 25 and w 2. Hours. PW > 25 and w 1. PNumber != w 2. PNumber 173

SQL: Target List Examples (2) n TARGET Lists may also contain the keyword DISTINCT – Since SQL does not treat relations as sets, duplicate tuples may appear, therefore DISTINCT is used to eliminate the duplicates n CQUERY 2: Show all distinct (different values) salaries that employees earn select from n distinct e. Salary EMPLOYEE e The above query also shows that the WHERE clause is optional (with missing WHERE, all tuples qualify) YV - Relational Calculus, SQL, QBE 174

SQL: Target List Examples (3) n The TARGET List may contain the wild character: “*” When a * is used, it implies that all attributes from the relation(s) should be retrieved n CQUERY 3: Show all employees in department number 4 select from where YV - Relational Calculus, SQL, QBE * EMPLOYEE e e. Dnumber = 4 175

SQL: Use of Tuple Variables n n n Relation names can be used instead of tuple variables Tuple variables can be implicit if the system can figure out which relation each attribute belongs to. CQUERY 4: For every project located in Athens, list the project name, the controlling department number and the department’s manager name select from where YV - Relational Calculus, SQL, QBE PName, DEPARTMENT. DNumber, Name EMPLOYEE, DEPARTMENT, PROJECT. DNumber = DEPARTMENT. DNumber and Mgr. SSN = SSN and Location = “athens” 176

SQL Qualification Examples -1 n QUALIFICATIONS: Each item in a qualification can be as general as: expression = expression n CQUERY 5: Find the names of employees whose salary is more than double the salary of some other employee (also show their name) select from where YV - Relational Calculus, SQL, QBE Name 1 = e 1. Name, Name 2 = e 1. Name EMPLOYEE e 1, EMPLOYEE e 2 2 * e 1. Salary < e 2. Salary 177

SQL Qualification Examples -2 n SQL provides direct support of several SET operations, like: – union – minus – intersect n CQUERY 6: Find the names of employees who work in department number 4 and earn at most 40000 (select from where Name EMPLOYEE DNumber = 4 ) minus Name EMPLOYEE Salary > 40000 ) YV - Relational Calculus, SQL, QBE 178

SQL Qualification Examples -3 n CQUERY 7: List all project names for projects that involve an employee whose name is “jenny” as a worker or as a manager of the department that controls the project (select PName from EMPLOYEE, PROJECT, DEPARTMENT where EMPLOYEE. DNumber=DEPARTMENT. DNumber and Mgr. SSN = SSN and Name = “jenny” ) union (select PName from EMPLOYEE, PROJECT, WORKS_ON where PROJECT. PNumber = WORKS_ON. PNumber and WORKS_ON. SSN=EMPLOYEE. SSN and Name = “jenny” ) YV - Relational Calculus, SQL, QBE 179

SQL Qualification Examples-4 n NESTING OF SQL QUERIES: A complete SELECT query (called the nested query) can be specified in the qualification of another query (called the outer query) n CQUERY 8: List all employees that work in the research department select from where YV - Relational Calculus, SQL, QBE Name EMPLOYEE DNumber in (select DNumber from DEPARTMENT where DName = “research” ) 180

SQL Qualification Examples-5 n CORRELATED NESTED Queries: If a condition in the qualification of a nested query references an attribute in the outer query, the two are said to be CORRELATED The result of the nested query is different for each tuple of the relation(s) in the outer query n CQUERY 9: List the name of each employee who has a dependent with the same sex as the employee select Name from EMPLOYEE e where e. SSN in (select d. SSN from DEPENDENT d where d. SSN = e. SSN and d. Sex = e. Sex ) YV - Relational Calculus, SQL, QBE 181

SQL Qualification Examples-6 n Any query that uses the IN comparison operator (tests for set membership) can always be expressed as a single block query (flat query) n CQUERY 9 a: List the name of each employee who has a dependent with the same sex as the employee select from where YV - Relational Calculus, SQL, QBE Name EMPLOYEE e, DEPENDENT d e. SSN = d. SSN and d. Sex = e. Sex ) 182

SQL Qualification Examples-7 n Similar connectives to IN are: t not in (tests for set non-membership) t OP any (OP relationship with some tuple in a set) t OP all (OP relationship with all tuples in a set) where OP Î { =, ¹, <, >, £, ³ } n CQUERY 10: List all employees that earn more than everybody in the research department select from where (select from where YV - Relational Calculus, SQL, QBE Name EMPLOYEE Salary > all Salary EMPLOYEE e, DEPARTMENT d e. DNumber = d. DNumber and DName = “research” ) 183

SQL Qualification Examples-8 n SQL also provides SET COMPARATORS: – contains, not contains (a set (not) being a superset) – exists, not exists (a set (not) being empty) n CQUERY 11: List all employees who work on all projects controlled by department number 4 select from where Name EMPLOYEE e (select w. PNumber from WORKS_ON where w. SSN = e. SSN) contains (select PNumber from PROJECT where DNumber = 4) YV - Relational Calculus, SQL, QBE 184

SQL Qualification Examples-9 n CQUERY 9 b: List the name of each employee who has a dependent with the same sex as the employee select from where n Name EMPLOYEE e exists (select * from DEPENDENT d where d. SSN=e. SSN and d. Sex = e. Sex) CQUERY 12: List the employees with no dependents select from where YV - Relational Calculus, SQL, QBE Name EMPLOYEE e not exists (select * from DEPENDENT d where d. SSN=e. SSN ) 185

SQL Aggregates and Groups-1 n SQL supports FIVE AGGREGATE FUNCTIONS (can be applied to any attribute X of a relation): t t t n count ( [DISTINCT] X) : number of unique values in X sum ( [DISTINCT] X) : sum of unique values in X avg ( [DISTINCT] X) : average of unique values in X max (X) : maximum value in X min (X) : minimum value in X Aggregates return a single value YV - Relational Calculus, SQL, QBE 186

SQL Aggregates and Groups-2 n Some SQL implementations do not allow more than one value in the target list n CQUERY 13: List the maximum salary, the minimum salary, and the average salary among all employees select from n max(Salary), min(Salary), avg(Salary EMPLOYEE QUERY 14: Find the number of employees select from YV - Relational Calculus, SQL, QBE count(*) EMPLOYEE 187

SQL Aggregates and Groups-3 n Qualified Aggregates: The set on which aggregates apply can be restricted by the where-clause n CQUERY 15: Find the average salary of employees in department with number 4 select from where YV - Relational Calculus, SQL, QBE avg(Salary) EMPLOYEE DNumber = 4 188

SQL Aggregates and Groups-4 n Aggregate Functions: Aggregates or groups of tuples are computed using the GROUP BY clause n CQUERY 16: In each department, find the minimum age of employees who earn more than 40000 select from where group by DNumber, max(Birth. Date) EMPLOYEE Salary > 40000 DNumber – Note that the grouping attributes MUST ALSO appear in the select clause YV - Relational Calculus, SQL, QBE 189

SQL Aggregates and Groups-5 n CQUERY 17: For each project, retrieve the project number, project name, and the number of employees that work on that project select from where group by n p. PNumber, p. PName, count(*) PROJECT p, WORKS_ON w p. PNumber = w. PNumber, PName In the above query, the grouping and functions are applied after joining the relations PROJECT and WORKS_ON. YV - Relational Calculus, SQL, QBE 190

SQL Aggregates and Groups-6 n HAVING CLAUSE: Qualifications that have to be satisfied by each group formed by the group by- clause are put in a HAVING clause n CQUERY 18: Find the average salary of employees born after 1950 for each department with more than 10 such employees select from where group by having YV - Relational Calculus, SQL, QBE DNumber, avg(Salary) EMPLOYEE Birth. Date > “ 1. 1. 51” DNumber count(*) > 10 191

SQL Aggregates and Groups-6 n CQUERY 19: Find the average salary of employees born after 1950 for each department with more than 10 employees select from where group by having e 1. DNumber, avg(e 1. Salary) EMPLOYEE e 1. Birth. Date > “ 1. 1. 51” e 1. DNumber 10 < any (select count(e 2. SSN) from EMPLOYEE e 2 where e 2. DNumber = e 1. DNumber ) YV - Relational Calculus, SQL, QBE 192

SQL Updates (1) n INSERT command insert into relation_name select-statement or insert into relation_name values (value_list) n CUPDATE 1: Insert a new department insert into DEPARTMENT values (6, “inventory”, 9879, “ 30. 5. 45”) YV - Relational Calculus, SQL, QBE 193

SQL Updates (2) n Suppose we have a relation DEPT_INFO as in: DEPT_INFO ( Dept. Name, No. Of. Empl, Total. Salary) n We can insert tuples in this relation with (CUPDATE 2): insert into DEPT_INFO select d. DName, count(*), sum(e. Salary) from DEPARTMENT d, EMPLOYEE e where d. DNumber=e. DNumber group by d. DName YV - Relational Calculus, SQL, QBE 194

SQL Updates (3) n DELETE command delete from relation_name where-qualification SEMANTICS: -- Execute the corresponding SELECT command then remove the resulting tuples from relation_name n CUPDATE 3: delete from EMPLOYEE where DNumber in YV - Relational Calculus, SQL, QBE (select DNumber from DEPARTMENT where DName = “admin”) 195

SQL Updates (4) n UPDATE command update relation_name set target_list where qualification SEMANTICS: -- Execute the two corresponding SELECT commands, then remove the old tuples from relation, then insert the new ones n CUPDATE 4: update EMPLOYEE set Salary = Salary * 1. 14 where DNumber in (select from where YV - Relational Calculus, SQL, QBE DNumber DEPARTMENT DName = “admin”) 196