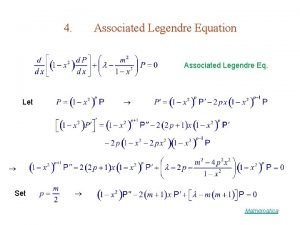4 Associated Legendre Equation Associated Legendre Eq Let
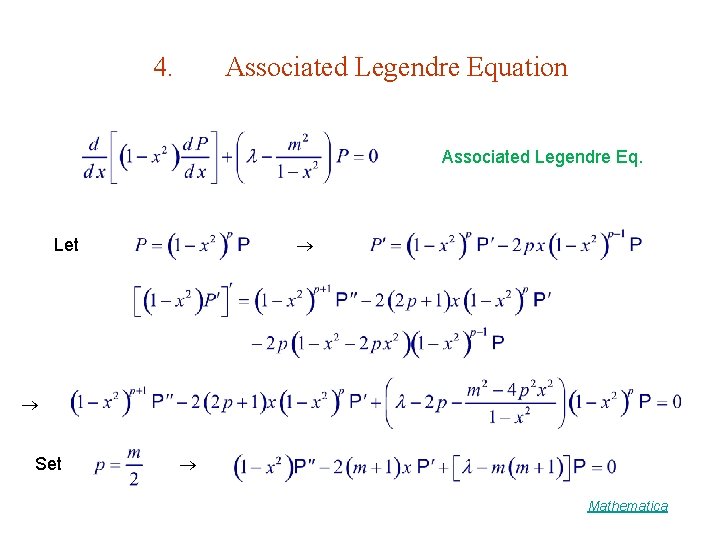



























![Fig. 15. 12. Shapes of [ Re Ylm ( , ) ]2 Surfaces are Fig. 15. 12. Shapes of [ Re Ylm ( , ) ]2 Surfaces are](https://slidetodoc.com/presentation_image/0c6932b57f999b233203300eb2791799/image-30.jpg)










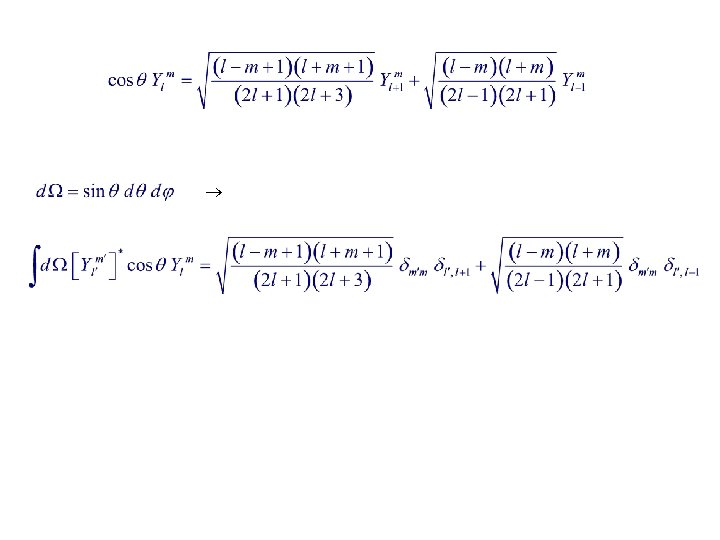








- Slides: 50
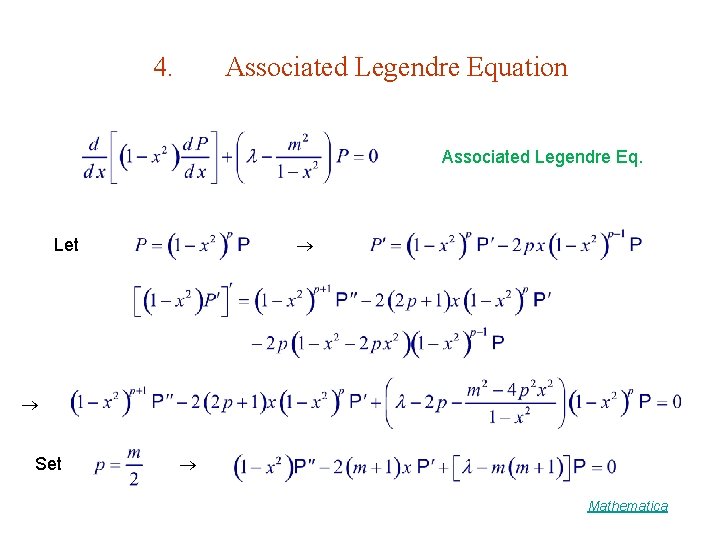
4. Associated Legendre Equation Associated Legendre Eq. Let Set Mathematica

Frobenius Series with indicial eqs. By definition, or Mathematica

Series diverges at x = 1 unless terminated. For s = 0 & a 1= 0 (even series) : ( l, m both even or both odd ) Mathematica For s = 1 & a 1=0 (odd series) : ( l, m one even & one odd ) Plm = Associated Legendre function

Relation to the Legendre Functions Generalized Leibniz’s rule :

Set Associated Legendre function : ( )m is called the Condon. Shortley phase. Including it in Plm means Ylm has it too. Rodrigues formula : Mathematica

Generating Function & Recurrence & ( Redundant since Plm is defined only for l |m| 0. )

as before

( Redundant since Plm is defined only for l |m| 0. ) &

Recurrence Relations for Plm (1) = (15. 88) (2) (1) : (3) (2) : (3) (15. 89)

Table 15. 3 Associated Legendre Functions Using one can generate all Plm (x) s from the Pl (x) s. Mathematica

Example 15. 4. 1. Recurrence Starting from Pmm (x) no negative powers of (x 1)

l=m l = m+k 1 E. g. , m = 2 :

Parity & Special Values Rodrigues formula : Parity Special Values : Ex. 15. 4 -5

Orthogonality Plm is the eigenfunction for eigenvalue of the Sturm-Liouville problem where Lm is hermitian Alternatively : (w=1)

No negative powers allowed For p q , let & only j = q ( x = + 1) or j = k q ( x = 1 ) terms can survive

p q: For j > m : For j < m + 1 :

p q: Only j = 2 m term survives

Ex. 13. 3. 3 B(p, q)

For fixed m, polynomials { Ppm (x) } are orthogonal with weight ( 1 x 2 )m. Similarly

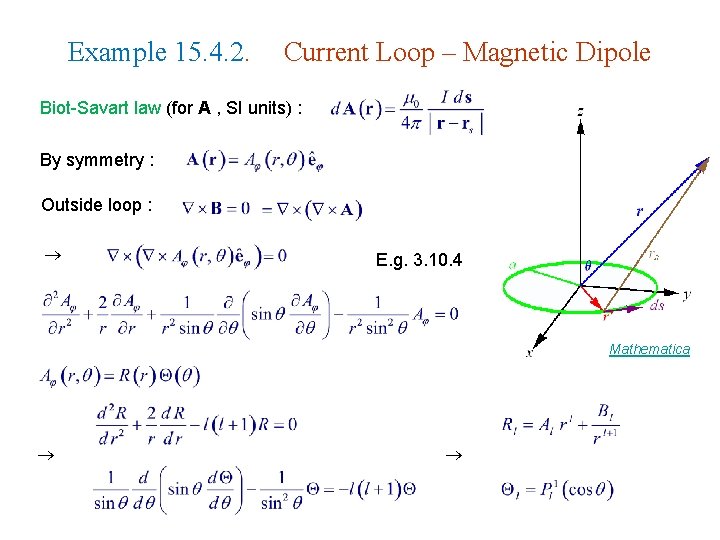
Example 15. 4. 2. Current Loop – Magnetic Dipole Biot-Savart law (for A , SI units) : By symmetry : Outside loop : E. g. 3. 10. 4 Mathematica

For r > a :

For r > a :

on z-axis : or (odd in z)

Biot-Savart law (SI units) : Cartesian coord:

For r > a :

s 0 1 2 s 1 3/2 15/8 s 0 1 2 s 1 3/4 5/8

Electric dipole :

5. Spherical Harmonics Laplace, Helmholtz, or central force Schrodinger eq. Set Orthonormal solutions

Orthonormality : Real valued form of : Spherical harmonics ( with Condon-Shortley phase via Plm )
![Fig 15 12 Shapes of Re Ylm 2 Surfaces are Fig. 15. 12. Shapes of [ Re Ylm ( , ) ]2 Surfaces are](https://slidetodoc.com/presentation_image/0c6932b57f999b233203300eb2791799/image-30.jpg)
Fig. 15. 12. Shapes of [ Re Ylm ( , ) ]2 Surfaces are given by Y 00 Y 10 Y 20 Y 11 Y 22 Y 21 Mathematica Y 30 Y 31 Y 32 Y 33

Cartesian Representations f is a polynomial Using one gets

Table 15. 4. Spherical Harmonics (with Condon-Shortley Phase ( ) ) m Mathematica Spherical. Harmonic. Y[l, m, , ] Mathematica

Mathematica

Overall Solutions Laplace eq. : Helmholtz eq. :

Laplace Expansion = eigenstates of the Sturm-Liouville problem S is a complete set of orthogonal functions on the unit sphere. Laplace series

Example 15. 5. 1. Spherical Harmonic Expansion Problem : Let the potential on the surface of a charge-free spherical region of radius r 0 be . Find the potential inside the region. regular at r = 0

Example 15. 5. 2. Laplace Series – Gravity Fields Gravity fields of the Earth, Moon, & Mars had been described as where [ see Morse & Feshbach, “Methods of Theoretical Physics”, Mc. Graw-Hill (53) ] See Ex. 15. 5. 6 for normalization Measured Earth Moon Mars C 20 (equatorial bulge) 1. 083 10 3 0. 200 10 3 1. 96 10 3 C 22 (azimuthal dep. ) 0. 16 10 5 2. 4 10 5 5 10 5 S 22 (azimuthal dep. ) 0. 09 10 5 0. 5 10 5 3 10 5

Symmetry of Solutions have less symmetry than the Hamiltonian due to the initial conditions. L 2 has spherical symmetry but none of Yl m ( l 0) does. { Yl m ; m = l, …, l } are eigenfunctions with the same eigenvalue l ( l + 1). { Yl m ; m = l, …, l } spans the eigen-space for eigenvalue l ( l + 1) has degeneracy = 2 l + 1. Same pt. in different coord. systems or different pts in same coord. system m degeneracy also occurs for the Laplace, Helmholtz, & central force Schrodinger eqs. see Chap. 16 for more

Example 15. 5. 3. Y 1 m Solutions for l = 1 at Arbitray Orientaion 1 0 1 Spherical Cartesian coordinates : Unit vector with directional cosine angles { , , } : Same pt. r, different coord. system.

Further Properties Special values: Recurrence ( straight from those for Plm ) :
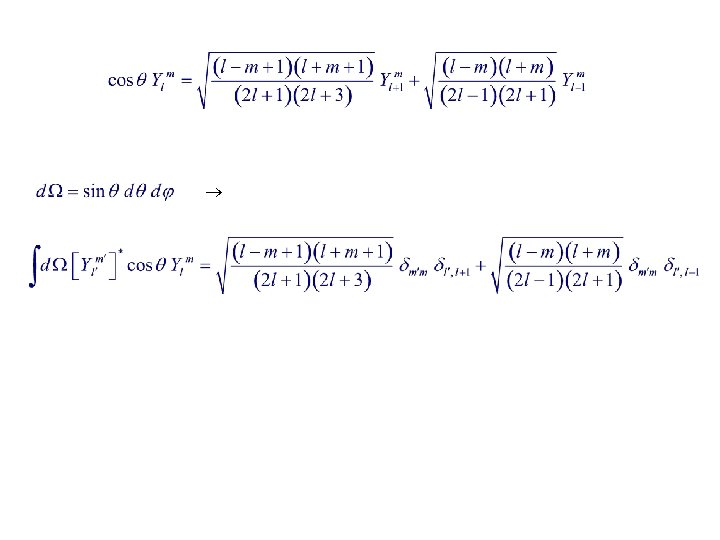

6. Legendre Functions of the Second Kind Alternate form : 2 nd solution ( § 7. 6 ) : where the Wronskian is

Mathematica Ql obeys the same recurrence relations as Pl.

for If we define Ql (x) to be real for real arguments, Replace Note: Legendre. Q in Mathematica retains the i term. for |x| > 1. For complex arguments, place the branch cut from z = 1 to z = +1. Values for arguments on the branch cut are given by the average of those on both sides of the cut.

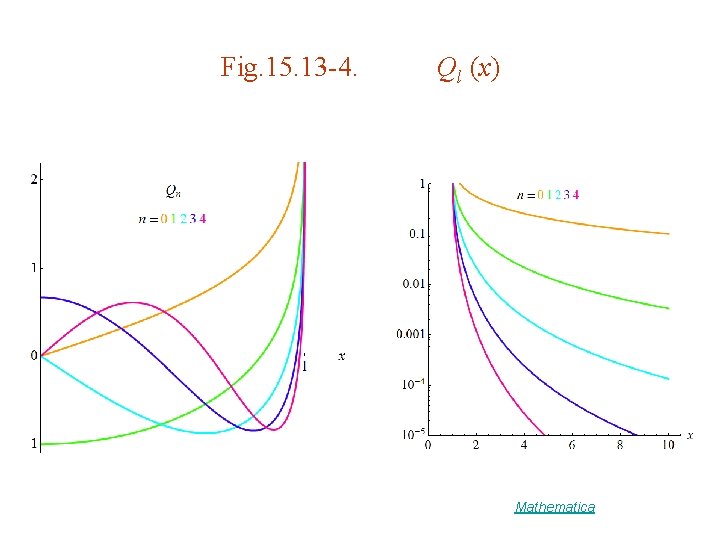
Fig. 15. 13 -4. Ql (x) Mathematica

Properties Parity : x = 0 is a regular point Special values : See next page Ex. 15. 6. 3

Alternate Formulations Singular points of the Legendre ODE are at ( Singularity at x = is removable ) Ql has power series in x that converges for |x| < 1. & power series in 1/x that converges for |x| > 1. Frobenius series : s = 0 for even l s = 1 for odd l series converges at x=1 s = 0 for odd l s = 1 for even l Ql even Ql odd Pl even Pl odd

s = 0 for odd l s = 1 for even l s = 1 , l = even s = 0 , l = odd Ql even Ql odd Ql even j = even a 1 = 0 bl = a 0 for Ql

Lowest order in x :

Similarly, one gets Mathematica which can be fitted as For series expansion in x for Ql , see Ex. 15. 6. 2 For series expansion in 1/x for Ql , see Ex. 15. 6. 3
 Associated legendre
Associated legendre John 10:22-28
John 10:22-28 Let's let them object to another one
Let's let them object to another one Let's go to my house
Let's go to my house Mark 4:23-24
Mark 4:23-24 Quadratura de gauss
Quadratura de gauss Polinomios de legendre
Polinomios de legendre Manon legendre
Manon legendre Romberg integrali
Romberg integrali Matthieu legendre
Matthieu legendre Grado relativo
Grado relativo Laguerre polynomials
Laguerre polynomials Legendre duplication formula proof
Legendre duplication formula proof Adrien-marie legendre
Adrien-marie legendre Charles palabino
Charles palabino Legendre transformation hamiltonian
Legendre transformation hamiltonian Matlab legendre polynomial
Matlab legendre polynomial Li rb k cs ba sr ca na
Li rb k cs ba sr ca na Eyring equation and arrhenius equation
Eyring equation and arrhenius equation Linear equation and quadratic equation
Linear equation and quadratic equation Linear equation and quadratic equation
Linear equation and quadratic equation What is euler equation
What is euler equation Linear differential equation
Linear differential equation Eyring equation and arrhenius equation
Eyring equation and arrhenius equation Eyring equation and arrhenius equation
Eyring equation and arrhenius equation Ionic equarion
Ionic equarion Yashpal committee report 1993
Yashpal committee report 1993 Laccolith shape
Laccolith shape Psychodynamic theory examples
Psychodynamic theory examples What encompasses all activities associated with the flow
What encompasses all activities associated with the flow Simple non inferential passages
Simple non inferential passages What is multigrade
What is multigrade Salt skin associated lymphoid tissue
Salt skin associated lymphoid tissue Northern ireland national flower
Northern ireland national flower Drawing and disbursing
Drawing and disbursing Colors associated with time
Colors associated with time Use the ipde process to separate hazards
Use the ipde process to separate hazards Dural septa
Dural septa Three types of word parts
Three types of word parts A encompasses all activities associated with the flow
A encompasses all activities associated with the flow Associated rack corporation
Associated rack corporation Types of nonverbal communication
Types of nonverbal communication Name something associated with china
Name something associated with china Sfr in 8051
Sfr in 8051 Spinal meninges and associated structures
Spinal meninges and associated structures Statements about the changgo
Statements about the changgo Big data analytics is usually associated with
Big data analytics is usually associated with What is definition in mathematical system
What is definition in mathematical system Ie register in 8051
Ie register in 8051 Chapter 17 oral pathology
Chapter 17 oral pathology Post office related words
Post office related words