5 1 The Unit Circle The Unit Circle

5. 1 The Unit Circle

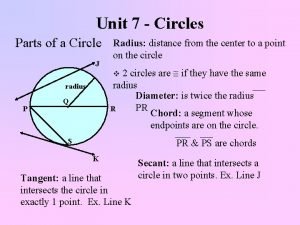
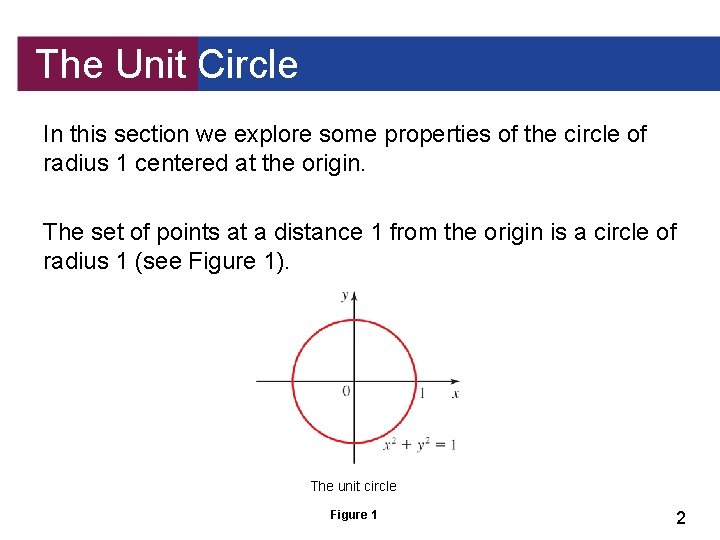
The Unit Circle In this section we explore some properties of the circle of radius 1 centered at the origin. The set of points at a distance 1 from the origin is a circle of radius 1 (see Figure 1). The unit circle Figure 1 2

The Unit Circle The equation of this circle is x 2 + y 2 = 1. 3

Example 1 – A Point on the Unit Circle Show that the point P is on the unit circle. Solution: We need to show that this point satisfies the equation of the unit circle, that is, x 2 + y 2 = 1. Since P is on the unit circle. 4

Terminal Points on the Unit Circle Suppose t is a real number. If t 0, let’s mark off a distance t along the unit circle, starting at the point (1, 0) and moving in a counterclockwise direction. If t < 0, we mark off a distance | t | in a clockwise direction (Figure 2). (a) Terminal point P(x, y) determined by t > 0 (b) Terminal point P(x, y) determined by t < 0 Figure 2 5

Terminal Points on the Unit Circle In this way we arrive at a point P(x, y) on the unit circle. The point P(x, y) obtained in this way is called the terminal point determined by the real number t. The circumference of the unit circle is C = 2 (1) = 2. So if a point starts at (1, 0) and moves counterclockwise all the way around the unit circle and returns to (1, 0), it travels a distance of 2. To move halfway around the circle, it travels a distance of (2 ) = . To move a quarter of the distance around the circle, it travels a distance of (2 ) = /2. 6

Terminal Points on the Unit Circle Where does the point end up when it travels these distances along the circle? From Figure 3 we see, for example, that when it travels a distance of starting at (1, 0), its terminal point is (– 1, 0). Terminal points determined by t = , , , and 2 Figure 3 7

Example 2 – Finding Terminal Points Find the terminal point on the unit circle determined by each real number t. (a) t = 3 (b) t = – (c) t = – Solution: From Figure 4 we get the following: Figure 4 8

Example 2 – Solution cont’d (a) The terminal point determined by 3 is (– 1, 0). (b) The terminal point determined by – is (– 1, 0). (c) The terminal point determined by – /2 is (0, – 1). Notice that different values of t can determine the same terminal point. 9

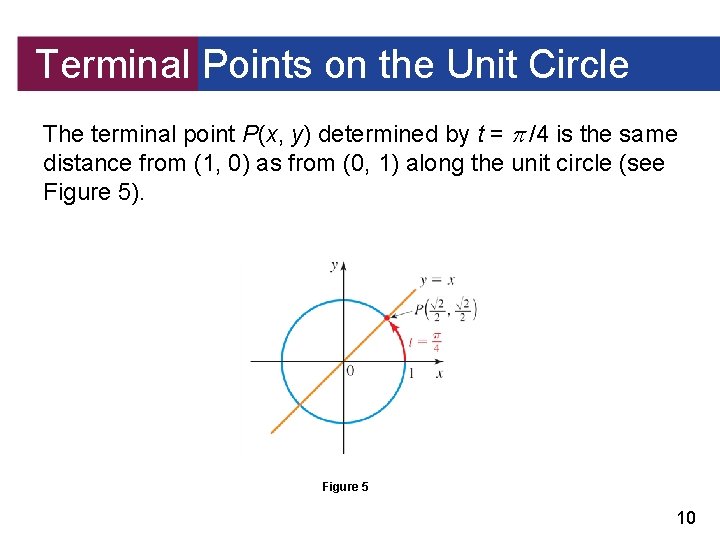
Terminal Points on the Unit Circle The terminal point P(x, y) determined by t = /4 is the same distance from (1, 0) as from (0, 1) along the unit circle (see Figure 5). Figure 5 10

Terminal Points on the Unit Circle Since the unit circle is symmetric with respect to the line y = x, it follows that P lies on the line y = x. So P is the point of intersection (in the Quadrant I) of the circle x 2 + y 2 = 1 and the line y = x. Substituting x for y in the equation of the circle, we get x 2 + x 2 = 1 2 x 2 = 1 Combine like terms 11

Terminal Points on the Unit Circle x 2 = x= Since P is in the Quadrant I, x = 1/ have y = 1/ also. Divide by 2 Take square roots and since y = x, we Thus the terminal point determined by /4 is 12

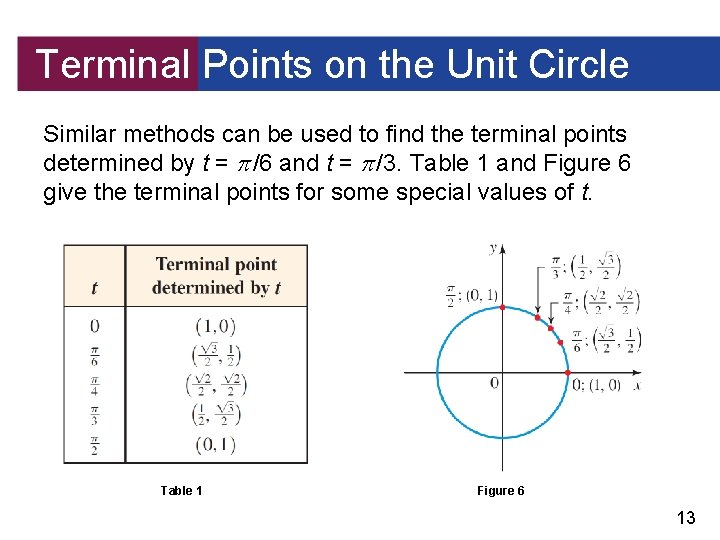
Terminal Points on the Unit Circle Similar methods can be used to find the terminal points determined by t = /6 and t = /3. Table 1 and Figure 6 give the terminal points for some special values of t. Table 1 Figure 6 13

Example 3 – Finding Terminal Points Find the terminal point determined by each given real number t. (a) t = (b) t = (c) t = Solution: (a) Let P be the terminal point determined by – /4, and let Q be the terminal point determined by /4. 14

Example 3 – Solution cont’d From Figure 7(a) we see that the point P has the same coordinates as Q except for sign. Since P is in Quadrant IV, its x-coordinate is positive and its y-coordinate is negative. Thus, the terminal point is P( /2, – /2). Figure 7(a) 15

Example 3 – Solution cont’d (b) Let P be the terminal point determined by 3 /4, and let Q be the terminal point determined by /4. From Figure 7(b) we see that the point P has the same coordinates as Q except for sign. Since P is in Quadrant II, its x-coordinate is negative and its y-coordinate is positive. Thus the terminal point is P(– /2, /2). Figure 7(b) 16

Example 3 – Solution cont’d (c) Let P be the terminal point determined by – 5 /6, and let Q be the terminal point determined by /6. From Figure 7(c) we see that the point P has the same coordinates as Q except for sign. Since P is in Quadrant III, its coordinates are both negative. Thus the terminal point is P. Figure 7(c) 17

The Reference Number From Examples 2 and 3 we see that to find a terminal point in any quadrant we need only know the “corresponding” terminal point in the first quadrant. We use the idea of the reference number to help us find terminal points. 18

The Reference Number Figure 8 shows that to find the reference number t, it’s helpful to know the quadrant in which the terminal point determined by t lies. The reference number t for t Figure 8 19

The Reference Number If the terminal point lies in Quadrant I or IV, where x is positive, we find t by moving along the circle to the positive x-axis. If it lies in Quadrant II or III, where x is negative, we find t by moving along the circle to the negative x-axis. 20

Example 4 – Finding Reference Numbers Find the reference number for each value of t. (a) t = (b) t = (c) t = (d) t = 5. 80 Solution: From Figure 9 we find the reference numbers as follows: (a) (c) (b) Figure 9 (d) 21

Example 4 – Solution cont’d (a) (b) (c) (d) 22

The Reference Number 23

Example 5 – Using Reference Numbers to Find Terminal Points Find the terminal point determined by each given real number t. (a) t = (b) t = (c) t = Solution: The reference numbers associated with these values of t were found in Example 4. 24

Example 5 – Solution cont’d (a) The reference number is t = /6, which determines the terminal point from Table 1. 25

Example 5 – Solution cont’d Since the terminal point determined by t is in Quadrant II, its x-coordinate is negative and its y-coordinate is positive. Thus the desired terminal point is (b) The reference number is t = /4, which determines the terminal point ( /2, /2) from Table 1. Since the terminal point is in Quadrant IV, its x-coordinate is positive and its y-coordinate is negative. 26

Example 5 – Solution cont’d Thus the desired terminal point is (c) The reference number is t = /3, which determines the terminal point from Table 1. Since the terminal point determined by t is in Quadrant III, its coordinates are both negative. Thus the desired terminal point is 27

The Reference Number Since the circumference of the unit circle is 2 , the terminal point determined by t is the same as that determined by t + 2 or t – 2. In general, we can add or subtract 2 any number of times without changing the terminal point determined by t. We use this observation in the next example to find terminal points for large t. 28

Example 6 – Finding the Terminal Point for Large t Find the terminal point determined by Solution: Since we see that the terminal point of t is the same as that of 5 /6 (that is, we subtract 4 ). 29

Example 6 – Solution So by Example 5(a) the terminal point is (See Figure 10. ) cont’d . Figure 10 30

5. 2 Trigonometric Functions of Real Numbers 31

Trigonometric Functions of Real Numbers A function is a rule that assigns to each real number another real number. In this section we use properties of the unit circle to define the trigonometric functions. 32

The Trigonometric Functions 33

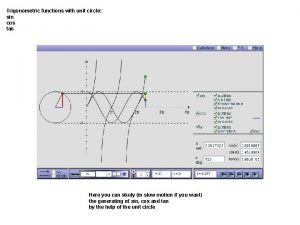
The Trigonometric Functions We know that to find the terminal point P(x, y) for a given real number t, we move a distance | t | along the unit circle, starting at the point (1, 0). We move in a counterclockwise direction if t is positive and in a clockwise direction if t is negative (see Figure 1). Figure 1 34

The Trigonometric Functions We now use the x- and y-coordinates of the point P(x, y) to define several functions. For instance, we define the function called sine by assigning to each real number t the y-coordinate of the terminal point P(x, y) determined by t. The functions cosine, tangent, cosecant, and cotangent are also defined by using the coordinates of P(x, y). 35

The Trigonometric Functions Because the trigonometric functions can be defined in terms of the unit circle, they are sometimes called the circular functions. 36

Example 1 – Evaluating Trigonometric Functions Find the six trigonometric functions of each given real number t. (a) t = (b) t = Solution: (a) From following table, we see that the terminal point determined by t = /3 is. (See Figure 2. ) Figure 2 37

Example 1 – Solution Since the coordinates are x = cont’d and y = we have (b) The terminal point determined by /2 is P(0, 1). (See Figure 3. ) Figure 3 38

Example 1 – Solution cont’d So But tan /2 and sec /2 are undefined because x = 0 appears in the denominator in each of their definitions. 39

The Trigonometric Functions Some special values of the trigonometric functions are listed in the table below. 40

The Trigonometric Functions Example 1 shows that some of the trigonometric functions fail to be defined for certain real numbers. So we need to determine their domains. The functions sine and cosine are defined for all values of t. Since the functions cotangent and cosecant have y in the denominator of their definitions, they are not defined whenever the y-coordinate of the terminal point P(x, y) determined by t is 0. This happens when t = n for any integer n, so their domains do not include these points. 41

The Trigonometric Functions The functions tangent and secant have x in the denominator in their definitions, so they are not defined whenever x = 0. This happens when t = ( /2) + n for any integer n. 42

Values of the Trigonometric Functions To compute values of the trigonometric functions for any real number t, we first determine their signs. The signs of the trigonometric functions depend on the quadrant in which the terminal point of t lies. For example, if the terminal point P(x, y) determined by t lies in Quadrant III, then its coordinates are both negative. So sin t, cos t, csc t, and sec t are all negative, whereas tan t and cot t are positive. 43

Values of the Trigonometric Functions You can check the other entries in the following box. 44

Values of the Trigonometric Functions 45

Example 2 – Evaluating Trigonometric Functions Find each value. (a) (b) (c) 46

Example 2(a) – Solution The reference number for 2 /3 is /3 (see Figure 4(a)). Figure 4(a) Since the terminal point of 2 /3 is in Quadrant II, cos(2 /3) is negative. Thus 47

Example 2(b) – Solution cont’d The reference number for – /3 is /3 (see Figure 4(b)). Figure 4(b) Since the terminal point of – /3 is in Quadrant IV, tan (– /3) is negative. Thus 48

Example 2(c) – Solution cont’d Since (19 /4) – 4 = 3 /4, the terminal points determined by 19 /4 and 3 /4 are the same. The reference number for 3 /4 is /4 (see Figure 4(c)). Figure 4(c) Since the terminal point of 3 /4 is in Quadrant II, sin(3 /4) is positive. 49

Example 2(c) – Solution cont’d Thus 50

Values of the Trigonometric Functions Fortunately, programmed directly into scientific calculators are mathematical procedures that find the values of sine, cosine, and tangent correct to the number of digits in the display. The calculator must be put in radian mode to evaluate these functions. To find values of cosecant, and cotangent using a calculator, we need to use the following reciprocal relations: 51

Values of the Trigonometric Functions These identities follow from the definitions of the trigonometric functions. For instance, since sin t = y and csc t = 1/y, we have csc t = 1/y = 1/(sin t). The others follow similarly. 52

Example 3 – Using a Calculator to Evaluate Trigonometric Functions Using a calculator, find the following. (a) sin 2. 2 (b) cos 1. 1 (c) cot 28 (d) csc 0. 98 Solution: Making sure our calculator is set to radian mode and rounding the results to six decimal places, we get (a) sin 2. 2 0. 808496 (b) cos 1. 1 0. 453596 53

Example 3 – Solution (c) cot 28 = (d) csc 0. 98 = cont’d – 3. 553286 1. 204098 54

Values of the Trigonometric Functions Let’s consider the relationship between the trigonometric functions of t and those of –t. From Figure 5 we see that sin(–t) = –y = –sin t cos(–t) = x = cos t tan(–t) = = = –tan t Figure 5 These equations show that sine and tangent are odd functions, whereas cosine is an even function. 55

Values of the Trigonometric Functions It’s easy to see that the reciprocal of an even function is even and the reciprocal of an odd function is odd. This fact, together with the reciprocal relations, completes our knowledge of the even-odd properties for all the trigonometric functions. 56

Example 4 – Even and Odd Trigonometric Functions Use the even-odd properties of the trigonometric function to determine each value. (a) (b) 57

Example 4 – Solution By the even-odd properties and Table 1, we have (a) Sine is odd Special values of the trigonometric functions Table 1 (b) Cosine is even 58

Fundamental Identities The trigonometric functions are related to each other through equations called trigonometric identities. We give the most important ones in the following box. 59

Fundamental Identities As their name indicates, the fundamental identities play a central role in trigonometry because we can use them to relate any trigonometric function to any other. So if we know the value of any one of the trigonometric functions at t, then we can find the values of all the others at t. 60

Example 5 – Finding All Trigonometric Functions from the Value of One If cos t = and t is in Quadrant IV, find the values of all the trigonometric functions at t. Solution: From the Pythagorean identities we have sin 2 t + cos 2 t = 1 sin 2 t + =1 sin 2 t = Substitute Solve for sin 2 t sin t = Take square roots 61

Example 5 – Solution cont’d Since this point is in Quadrant IV, sin t is negative, so sin t =. Now that we know both sin t and cos t, we can find the values of the other trigonometric functions using the reciprocal identities. 62

6. 1 Angle Measure 63

Angle Measure An angle AOB consists of two rays R 1 and R 2 with a common vertex O (see Figure 1). We often interpret an angle as a rotation of the ray R 1 onto R 2. Negative angle Positive angle Figure 1 64

Angle Measure In this case R 1 is called the initial side, and R 2 is called the terminal side of the angle. If the rotation is counterclockwise, the angle is considered positive, and if the rotation is clockwise, the angle is considered negative. 65

Angle Measure The measure of an angle is the amount of rotation about the vertex required to move R 1 onto R 2. Intuitively, this is how much the angle “opens. ” One unit of measurement for angles is the degree. An angle of measure 1 degree is formed by rotating the initial side of a complete revolution. In calculus and other branches of mathematics a more natural method of measuring angles is used: radian measure. 66

Angle Measure Figure 2 67

Angle Measure The circumference of the circle of radius 1 is 2 , so a complete revolution has measure 2 rad, a straight angle has measure rad, and a right angle has measure /2 rad. An angle that is subtended by an arc of length 2 along the unit circle has radian measure 2 (see Figure 3). Radian measure Figure 3 68

Angle Measure 69

Example 1 – Converting Between Radians and Degrees (a) Express 60 in radians. (b) Express rad in degrees. Solution: The relationship between degrees and radians gives (a) 60 (b) = 30 70

Angle Measure A note on terminology: We often use a phrase such as “a 30 angle” to mean an angle whose measure is 30. Also, for an angle we write = 30 or = /6 to mean the measure of is 30 or /6 rad. When no unit is given, the angle is assumed to be measured in radians. 71

Angles in Standard Position An angle is in standard position if it is drawn in the xy-plane with its vertex at the origin and its initial side on the positive x-axis. Figure 5 gives examples of angles in standard position. (a) (b) (c) (d) Angles in standard position Figure 5 72

Angles in Standard Position Two angles in standard position are coterminal if their sides coincide. In Figure 5 the angles in (a) and (c) are coterminal. 73

Example 2 – Coterminal Angles (a) Find angles that are coterminal with the angle = 30 in standard position. (b) Find angles that are coterminal with the angle = standard position. in Solution: (a) To find positive angles that are coterminal with , we add any multiple of 360. 74

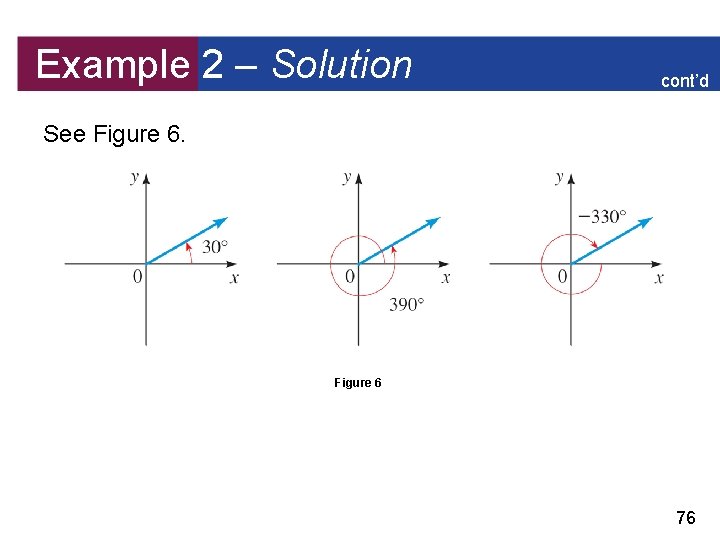
Example 2 – Solution cont’d Thus 30° + 360° = 390° and 30° + 720° = 750° are coterminal with = 30. To find negative angles that are coterminal with , we subtract any multiple of 360°. Thus 30° – 360° = – 330° and 30° – 720° = – 690° are coterminal with . 75

Example 2 – Solution cont’d See Figure 6 76

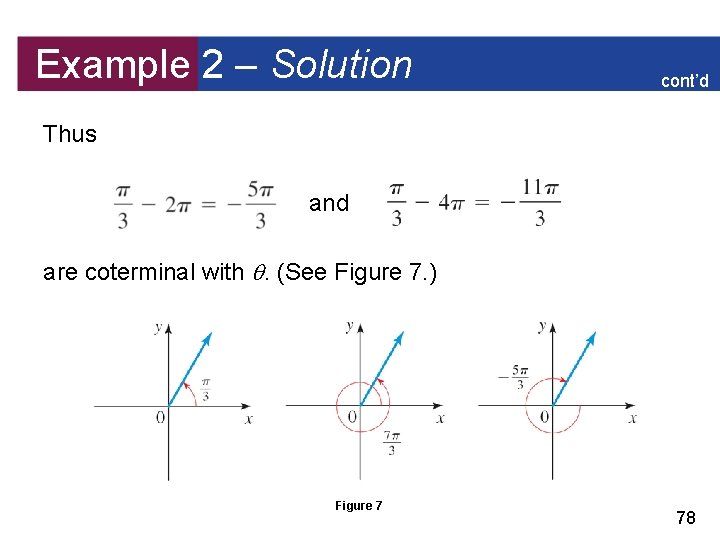
Example 2 – Solution cont’d (b) To find positive angles that are coterminal with , we add any multiple of 2. Thus and are coterminal with = /3. To find negative angles that are coterminal with , we subtract any multiple of 2. 77

Example 2 – Solution cont’d Thus and are coterminal with . (See Figure 7. ) Figure 7 78

Length of a Circular Arc Solving for , we get the important formula 79

Length of a Circular Arc This formula allows us to define radian measure using a circle of any radius r : The radian measure of an angle is s/r, where s is the length of the circular arc that subtends in a circle of radius r (see Figure 10). The radian measure of is the number of “radiuses” that can fit in the arc that subtends ; hence the term radian. Figure 10 80

Example 3 – Arc Length and Angle Measure (a) Find the length of an arc of a circle with radius 10 m that subtends a central angle of 30. (b) A central angle in a circle of radius 4 m is subtended by an arc of length 6 m. Find the measure of in radians. Solution: (a) From Example 1(b) we see that 30 = /6 rad. So the length of the arc is s = r = = 81

Example 3 – Solution cont’d (b) By the formula = s/r we have 82

Area of a Circular Sector 83

Example 4 – Area of a Sector Find the area of a sector of a circle with central angle 60 if the radius of the circle is 3 m. Solution: To use the formula for the area of a circular sector, we must find the central angle of the sector in radians: 60° = 60( /180) rad = /3 rad. Thus the area of the sector is 84

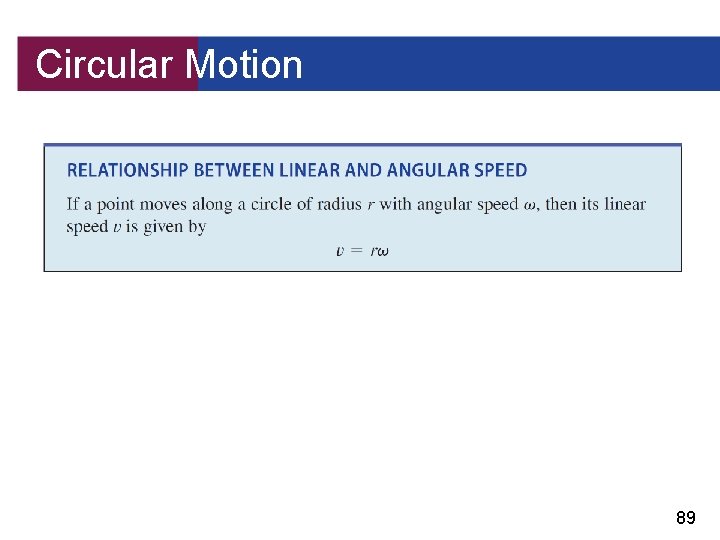
Circular Motion Suppose a point moves along a circle as shown in Figure 12. There are two ways to describe the motion of the point: linear speed angular speed. Linear speed is the rate at which the distance traveled is changing, so linear speed is the distance traveled divided by the time elapsed. Figure 12 85

Circular Motion Angular speed is the rate at which the central angle is changing, so angular speed is the number of radians this angle changes divided by the time elapsed. 86

Example 5 – Finding Linear and Angular Speed A boy rotates a stone in a 3 -ft-long sling at the rate of 15 revolutions every 10 seconds. Find the angular and linear velocities of the stone. Solution: In 10 s the angle changes by 15 2 = 30 rad. So the angular speed of the stone is 87

Example 5 – Solution cont’d The distance traveled by the stone in 10 s is s = 15 2 r = 15 2 3 = 90 ft. So the linear speed of the stone is 88

Circular Motion 89

Example 6 – Finding Linear Speed from Angular Speed A woman is riding a bicycle whose wheels are 26 in. in diameter. If the wheels rotate at 125 revolutions per minute (rpm), find the speed (in mi/h) at which she is traveling. Solution: The angular speed of the wheels is 2 125 = 250 rad/min. Since the wheels have radius 13 in. (half the diameter), the linear speed is = r = 13 250 10, 210. 2 in. /min 90

Example 6 – Solution cont’d Since there are 12 inches per foot, 5280 feet per mile, and 60 minutes per hour, her speed in miles per hour is 9. 7 mi/h 91