Similarity Trigonometric Functions The Unit Circle Similarity Same

Similarity Trigonometric Functions & The Unit Circle

Similarity • Same Shape – Sides Proportional – ALL angles congruent (same measure) – ALL SIDES PROPORTIONAL (SAME Ratio) Two polygons are similar polygons if and only if their corresponding angles are congruent and their corresponding side lengths are proportional.

Example 1: Describing Similar Polygons Identify the pairs of congruent angles and corresponding sides. N Q and P R. By the Third Angles Theorem, M T. 0. 5

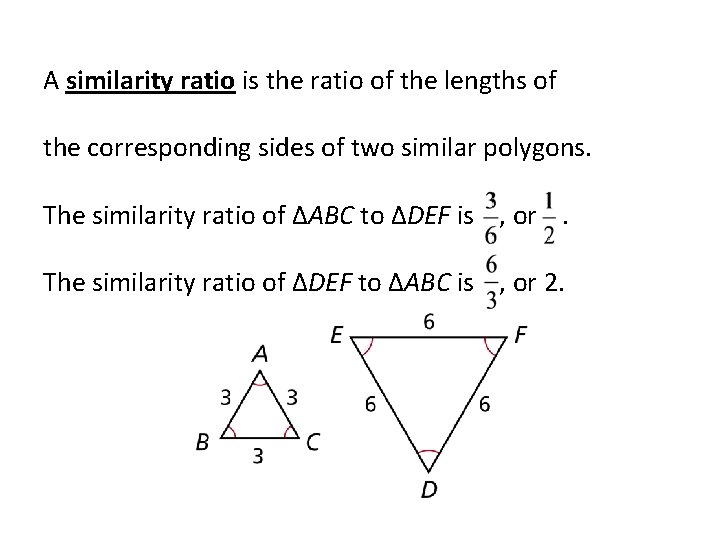
A similarity ratio is the ratio of the lengths of the corresponding sides of two similar polygons. The similarity ratio of ∆ABC to ∆DEF is , or. The similarity ratio of ∆DEF to ∆ABC is , or 2.

Check It Out! Example 2 Determine if ∆JLM ~ ∆NPS. If so, write the similarity ratio and a similarity statement. Step 1 Identify pairs of congruent angles. N M, L P, S J

Check It Out! Example 2 Continued Step 2 Compare corresponding sides. Thus the similarity ratio is , and ∆LMJ ~ ∆PNS.

Example 3: Hobby Application Find the length of the model to the nearest tenth of a centimeter. Let x be the length of the model in centimeters. The rectangular model of the racing car is similar to the rectangular racing car, so the corresponding lengths are proportional.

Using Similarity • Example – Shadows & Measurement – Tyler wants to find the height of a telephone pole. He measured the pole’s shadow and his own shadow then made a diagram. What is the height of the pole? Helpful Hint Whenever dimensions are given in both feet and inches, you must convert them to either feet or inches before doing any calculations.

Using Proportional Relationships

Example: Using Ratios to Find Perimeters and Areas Given that ∆LMN: ∆QRT, find the perimeter P and area A of ∆QRS. The similarity ratio of ∆LMN to ∆QRS is By the Proportional Perimeters and Areas Theorem, the ratio of the triangles’ perimeters is also of the triangles’ areas is , and the ratio

Example Continued Perimeter 13 P = 36(9. 1) P = 25. 2 Area 132 A = (9. 1)2(60) A = 29. 4 cm 2 The perimeter of ∆QRS is 25. 2 cm, and the area is 29. 4 cm 2.

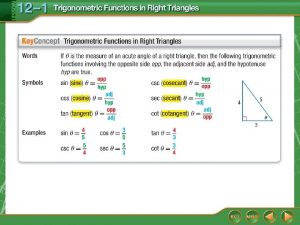
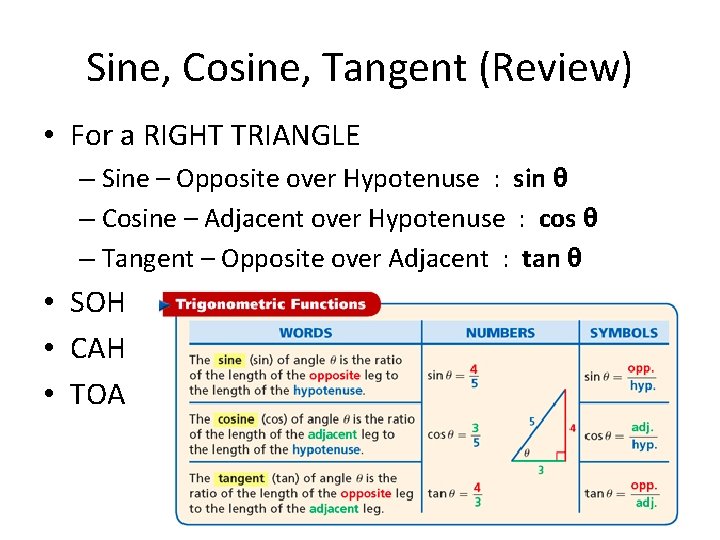
Sine, Cosine, Tangent (Review) • For a RIGHT TRIANGLE – Sine – Opposite over Hypotenuse : sin θ – Cosine – Adjacent over Hypotenuse : cos θ – Tangent – Opposite over Adjacent : tan θ • SOH • CAH • TOA

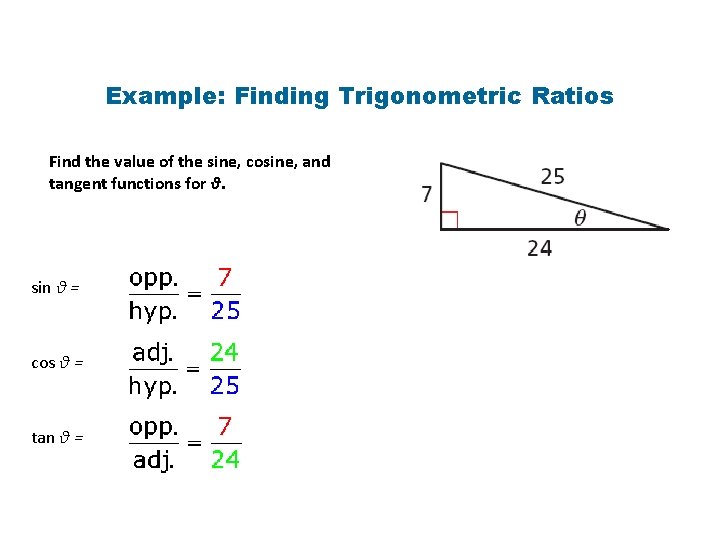
Example: Finding Trigonometric Ratios Find the value of the sine, cosine, and tangent functions for θ. sin θ = cos θ = tan θ =

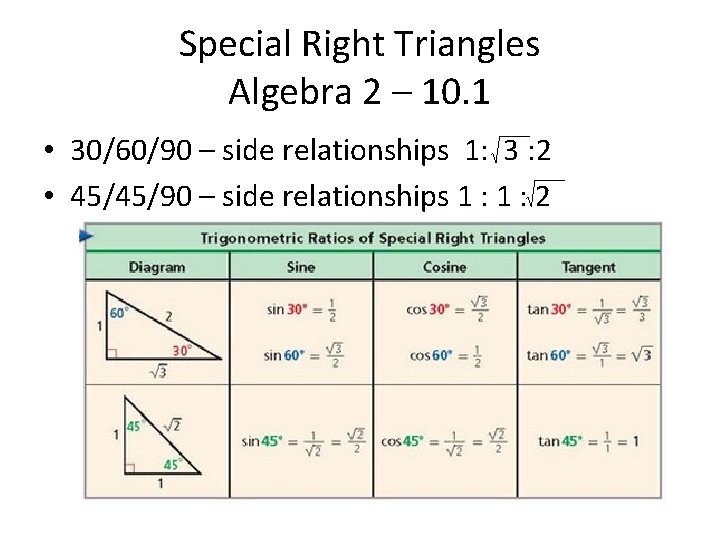
Special Right Triangles Algebra 2 – 10. 1 • 30/60/90 – side relationships 1: 3 : 2 • 45/45/90 – side relationships 1 : 2

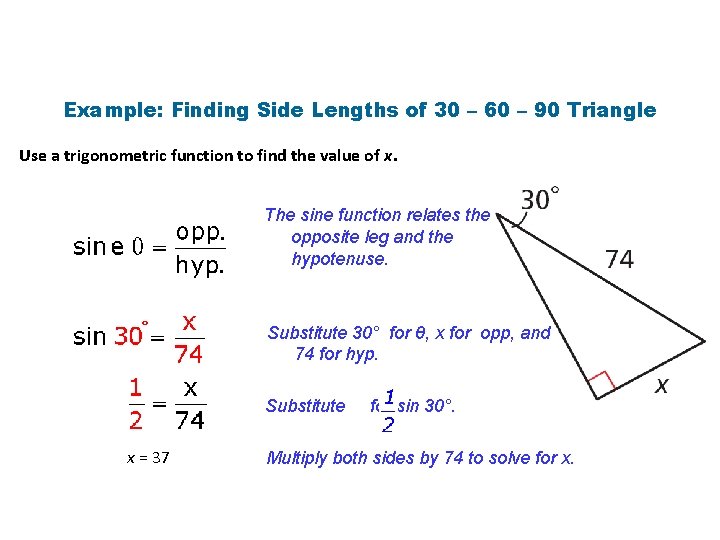
Example: Finding Side Lengths of 30 – 60 – 90 Triangle Use a trigonometric function to find the value of x. The sine function relates the opposite leg and the hypotenuse. ° Substitute 30° for θ, x for opp, and 74 for hyp. Substitute x = 37 for sin 30°. Multiply both sides by 74 to solve for x.

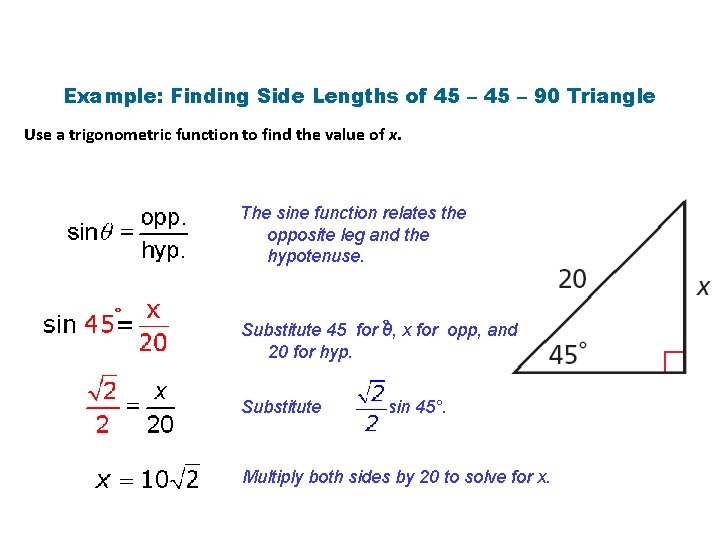
Example: Finding Side Lengths of 45 – 90 Triangle Use a trigonometric function to find the value of x. The sine function relates the opposite leg and the hypotenuse. ° ° x for opp, and Substitute 45 for θ, 20 for hyp. Substitute for sin 45°. Multiply both sides by 20 to solve for x.

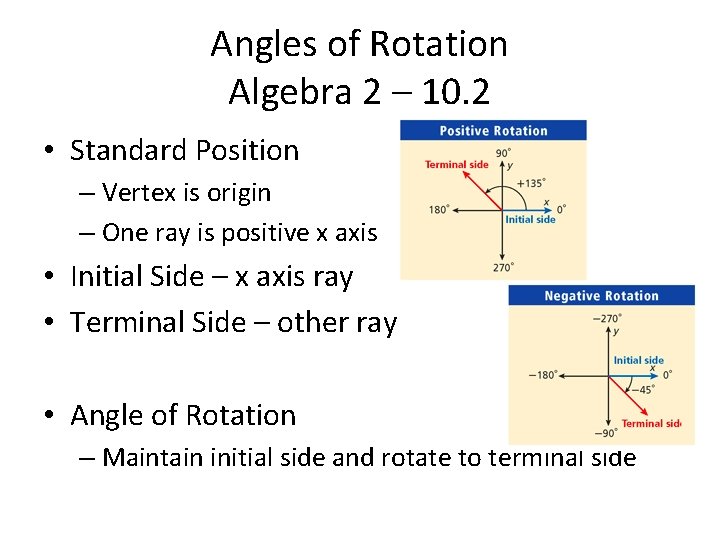
Angles of Rotation Algebra 2 – 10. 2 • Standard Position – Vertex is origin – One ray is positive x axis • Initial Side – x axis ray • Terminal Side – other ray • Angle of Rotation – Maintain initial side and rotate to terminal side

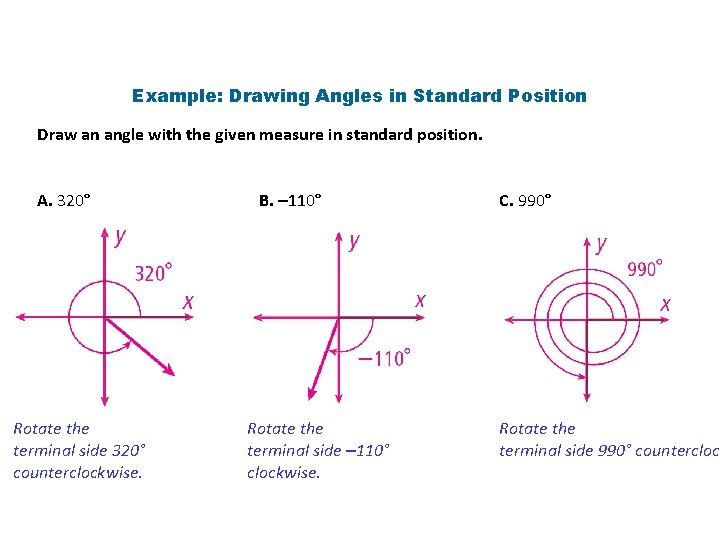
Example: Drawing Angles in Standard Position Draw an angle with the given measure in standard position. A. 320° Rotate the terminal side 320° counterclockwise. B. – 110° Rotate the terminal side – 110° clockwise. C. 990° Rotate the terminal side 990° counterclock

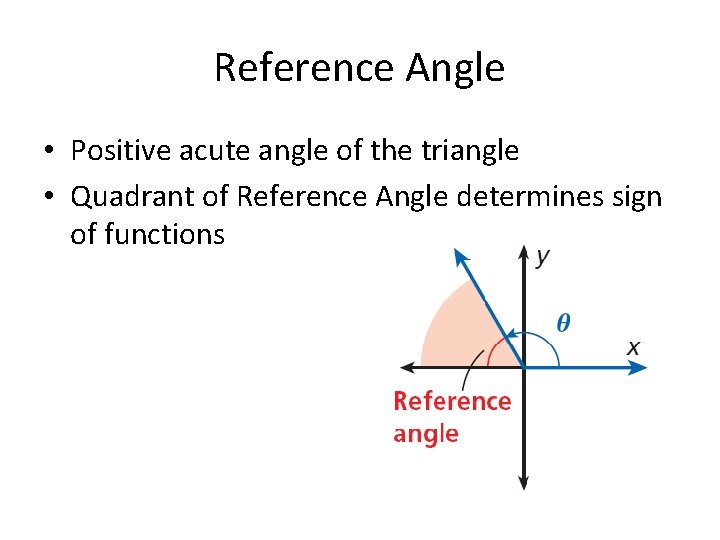
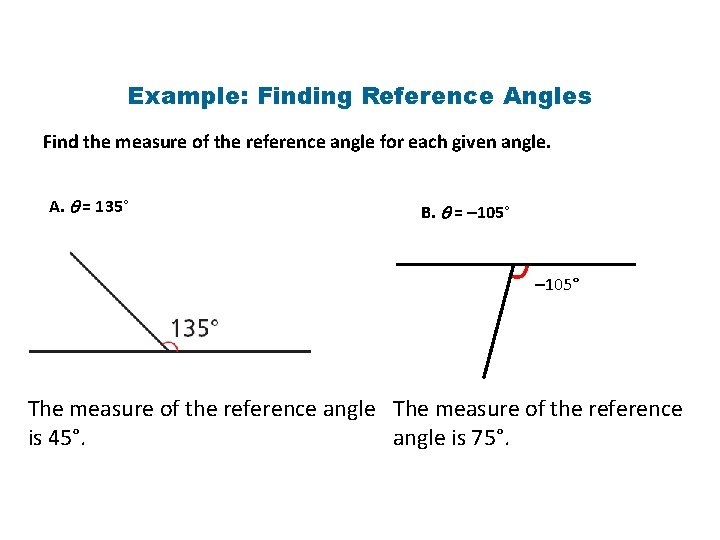
Reference Angle • Positive acute angle of the triangle • Quadrant of Reference Angle determines sign of functions

Example: Finding Reference Angles Find the measure of the reference angle for each given angle. A. = 135° B. = – 105° The measure of the reference angle The measure of the reference is 45°. angle is 75°.

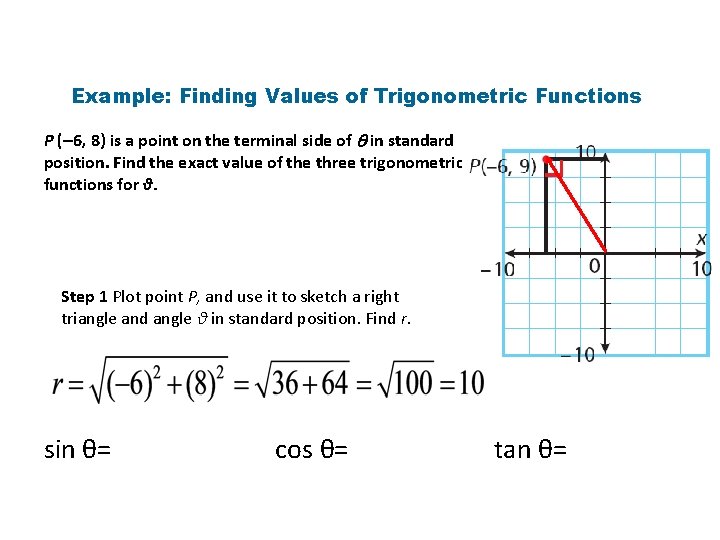
Reference Angle To determine the value of the trigonometric functions for an angle θ in standard position, begin by selecting a point P with coordinates (x, y) on the terminal side of the angle. The distance r from point P to the origin is given by.

Trig to Circles Algebra 2 – 10. 2 • If vertex is (0, 0) - trig uses x and y coordinates of point – Radius (r) is – Sine is y/r, Cosine is x/r, and Tangent is y/x

Example: Finding Values of Trigonometric Functions P (– 6, 8) is a point on the terminal side of in standard position. Find the exact value of the three trigonometric functions for θ. Step 1 Plot point P, and use it to sketch a right triangle and angle θ in standard position. Find r. sin θ= cos θ= tan θ=

Examples • Use the following coordinates to determine the trigonometric functions (sin, cos, tan): 1. 2. 3. 4. (3, 4) (-3, -4) (3, -4)

Signs in Quadrants • The location of the reference angle determines the sign of the functions

Radians and Degrees Algebra 2 – 10. 3 • Radian – Angle measure based on arc length – Circumference of circle = 2πr – Complete revolution of circle = 360 o • Relationship of radians to degrees is 2π = 3600

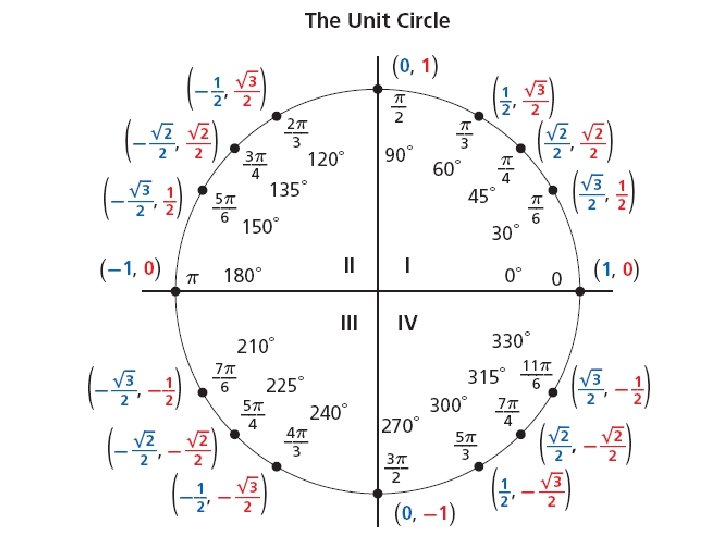
Unit Circle Algebra 2 – 10. 3 • Circle with a radius of 1 • Relation of radians, degrees and the sine and cosine of the related angles • Coordinates of point on circle are (cosθ, sinθ) – Cosine is the x coordinate – Sine is the y coordinate • Use 30 -60 -90 & 45 -45 -90 triangles

Building Unit Circle

Unit Circle

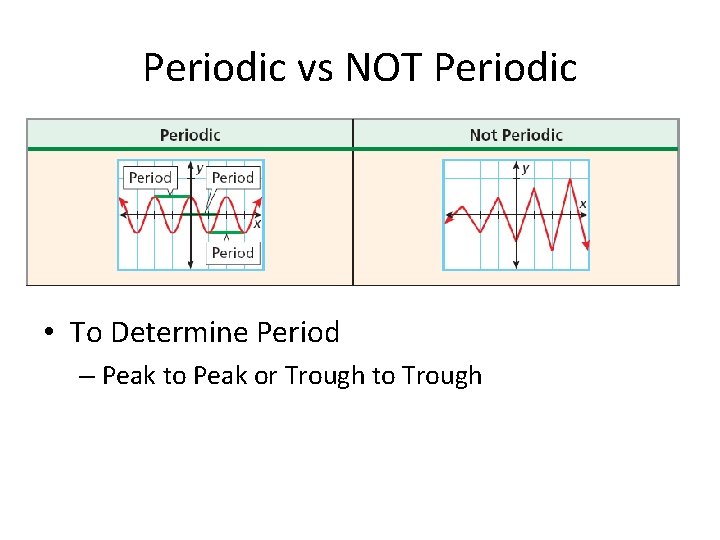
Graphing Sin/Cos Functions Algebra 2 – 11. 1 • Periodic – repeats exactly at a given interval – Intervals are called cycles – Length of the cycle is the period • Sin & Cos are Periodic – Values are the y & x values on unit circle – Period is 2π • 1 complete rotation

Periodic vs NOT Periodic • To Determine Period – Peak to Peak or Trough to Trough

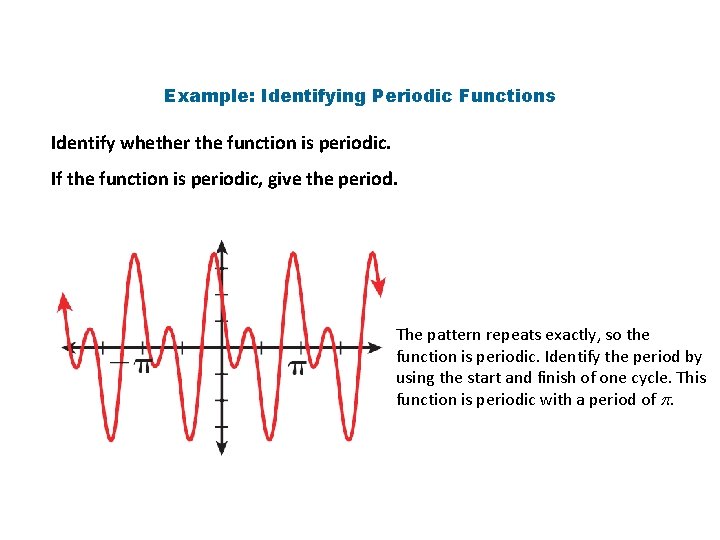
Example: Identifying Periodic Functions Identify whether the function is periodic. If the function is periodic, give the period. The pattern repeats exactly, so the function is periodic. Identify the period by using the start and finish of one cycle. This function is periodic with a period of .

Sin & Cos • Sin & Cos are Periodic – Values are the y & x values on unit circle – Period is 2π - 1 complete rotation

Amplitude • The amplitude of sine and cosine functions is half of the difference between the maximum and minimum values of the function. The amplitude is always positive. • This will be the difference from neautral (or 0) to the peak or trough or ½ the distance from the peak to trough

Transformations • Changing the Amplitude and Period – Amplitude is indicated by the a value (in front) – Period is the b value in front of the x (2π/b)

To Graph Sine/Cosine Functions • Determine the Peak & Trough Value • Determine the Period – Peak-peak/trough-trough • Set up a table – 5 columns – 2 rows • Enter start & end of period in top then cut in half then quarters – these are the x values • Fill in the y values (peak, trough & neutral) where they occur

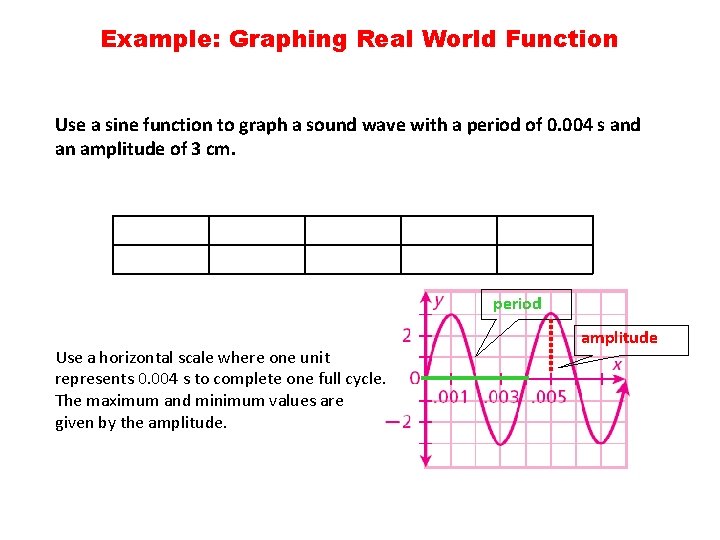
Example: Graphing Real World Function Use a sine function to graph a sound wave with a period of 0. 004 s and an amplitude of 3 cm. period Use a horizontal scale where one unit represents 0. 004 s to complete one full cycle. The maximum and minimum values are given by the amplitude

Other Transformations • Vertical or Phase Shift – up/down or left/right – h (left/right) and k (up/down) values in function – Primarily focus on Vertical (Up/Down) • Set a new neutral or Zero value • y = sin(x – h) + k • y = cos(x – h) + k. • Vertical translation by k units moves the graph up (k > 0) or down (k < 0)

Reciprocals of Sin/Cos/Tan • Reciprocal of Sine is Cosecant = 1/Sin – Hypotenuse over Opposite : csc • Reciprocal of Cosine is Secant = 1/Cos – Hypotenuse over Adjacent : sec • Reciprocal of Tangent is Cotangent = 1/Tan – Adjacent over Opposite : cot

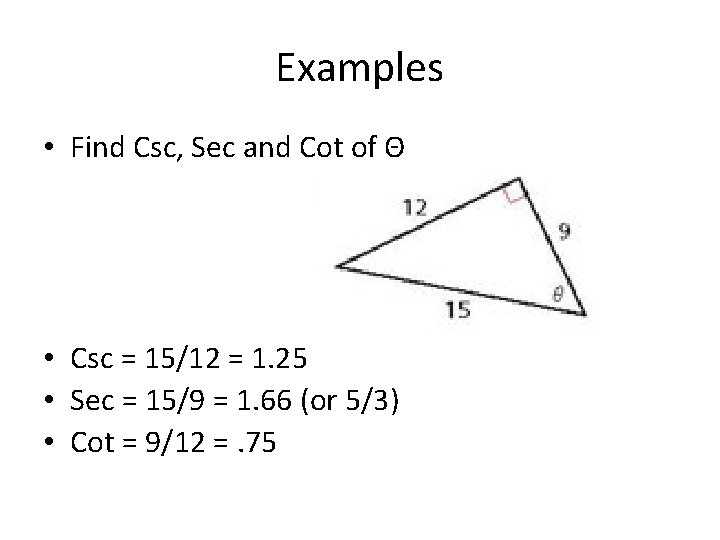
Examples • Find Csc, Sec and Cot of Θ • Csc = 15/12 = 1. 25 • Sec = 15/9 = 1. 66 (or 5/3) • Cot = 9/12 =. 75

Helpful Hint In each reciprocal pair of trigonometric functions, there is exactly one “co”

Trigonometric Identities Algebra 2 – 11. 2 • Use to compare and simplify trigonometric functions • Based on following table and algebraic solving – Use steps (like proofs) to justify relationships

Trig Identity Examples • : sinθcotθ = cosθ • : secθ – tanθ sinθ • Using calculator : – Enter into Y 1 & Y 2 – Compare Graphs

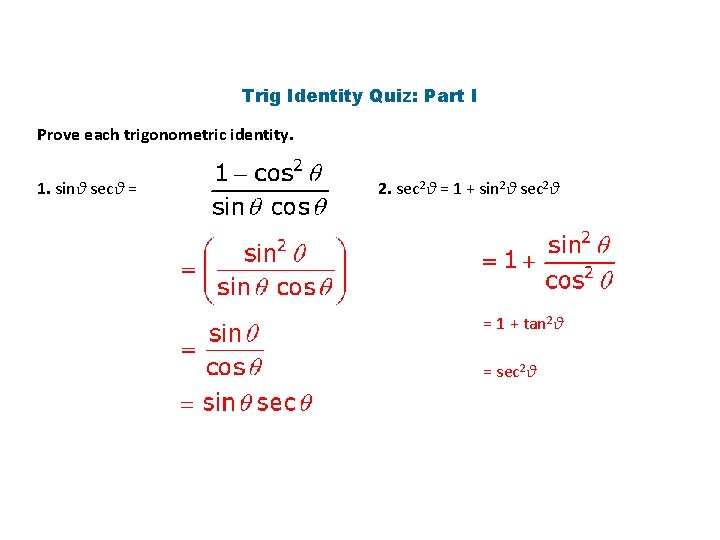
Trig Identity Quiz: Part I Prove each trigonometric identity. 1. sinθ secθ = 2. sec 2θ = 1 + sin 2θ sec 2θ = 1 + tan 2θ = sec 2θ

Trig Identity Quiz: Part II Rewrite each expression in terms of cos θ, and simplify. 3. sin 2θ cot 2θ secθ cosθ 4. 2 cosθ

Inverse Trig Functions • Going from value to angle measure • On calculator – sin-1(a) or cos-1(a) or tan-1(a) • Get there by 2 nd SIN/COS/TAN then enter the value in the parentheses – Value for sin/cos must be -1≤a≤ 1 • Example: – Find m<θ : sinθ = 7/14 : sinθ =. 5 : sin-1(. 5) = 7 14 θ

Restrictions on Inverse Functions • Domains & Ranges are restricted as follows: