Definition of an angle Terminal Ray Counter clockwise

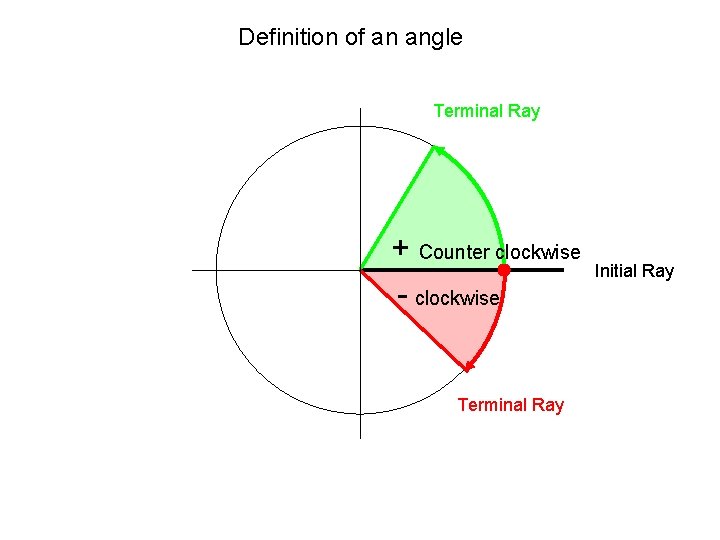
Definition of an angle Terminal Ray + Counter clockwise - clockwise Terminal Ray Initial Ray

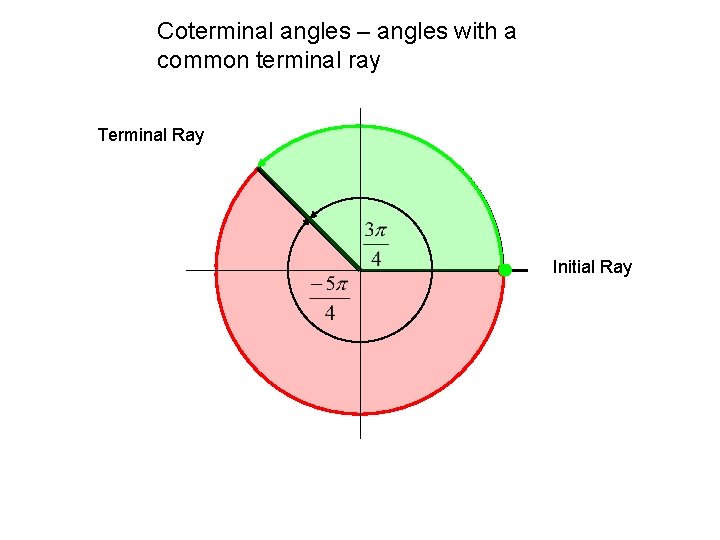
Coterminal angles – angles with a common terminal ray Terminal Ray Initial Ray

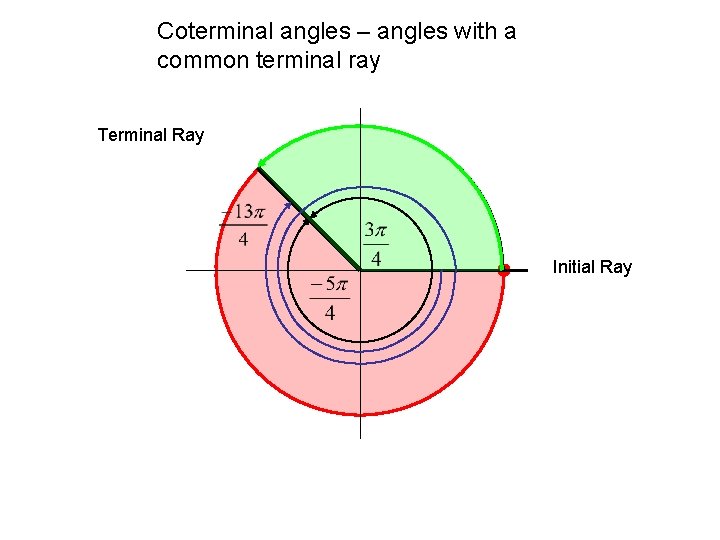
Coterminal angles – angles with a common terminal ray Terminal Ray Initial Ray

Radian Measure

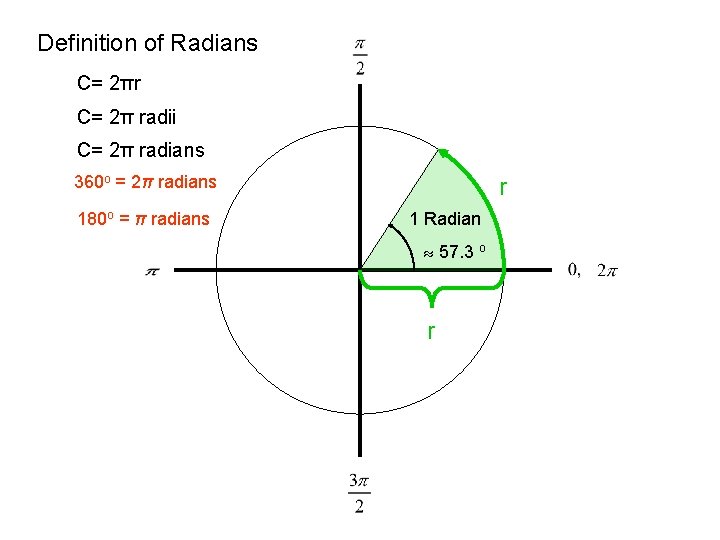
Definition of Radians C= 2πr C= 2π radii C= 2π radians 360 o = 2π radians 180 o = π radians r 1 Radian 57. 3 o r

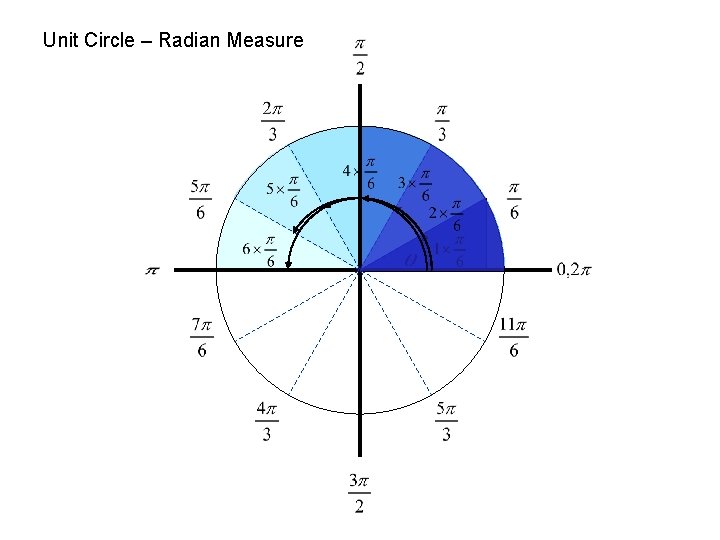
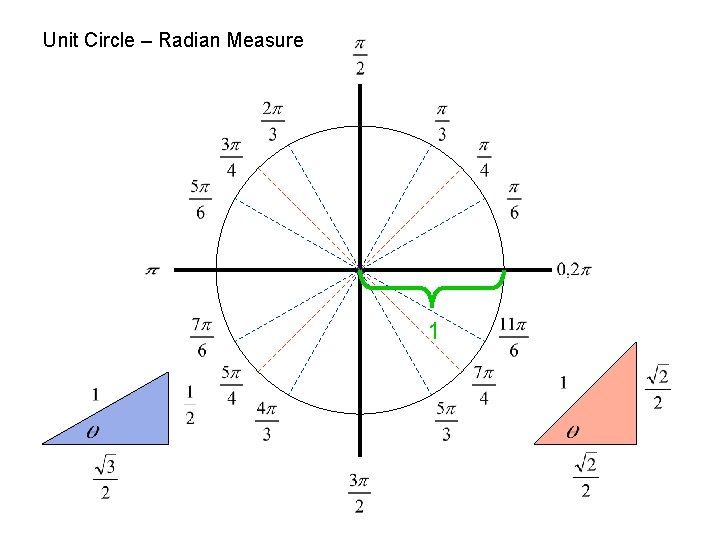
Unit Circle – Radian Measure

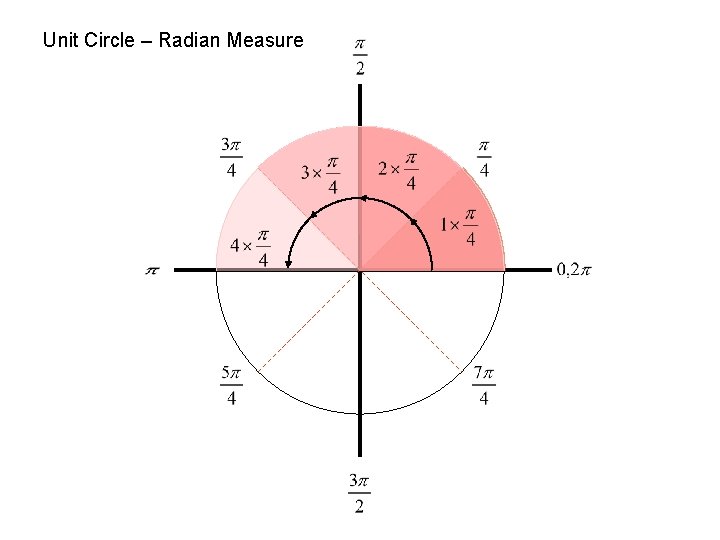
Unit Circle – Radian Measure

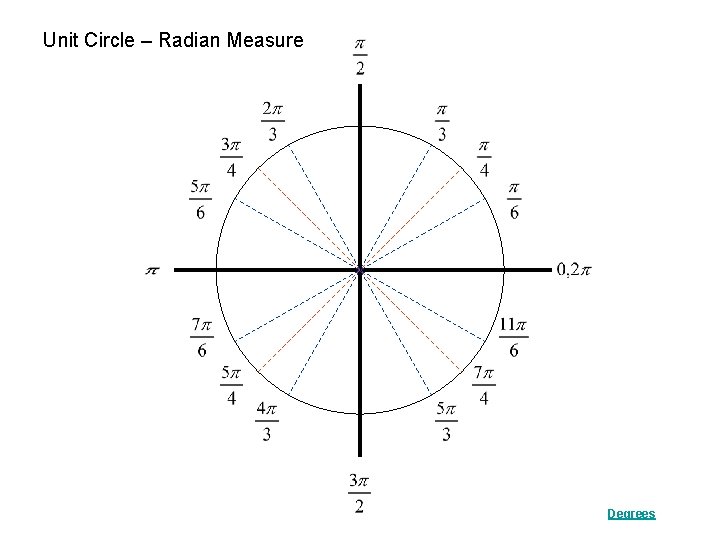
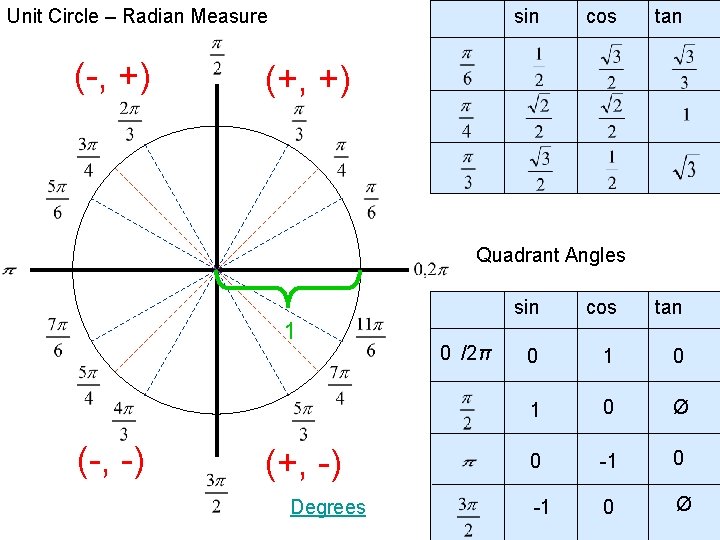
Unit Circle – Radian Measure Degrees

Converting Degrees ↔ Radians Converts degrees to Radians Recall Converts Radians to degrees more examples

Trigonometric Ratios

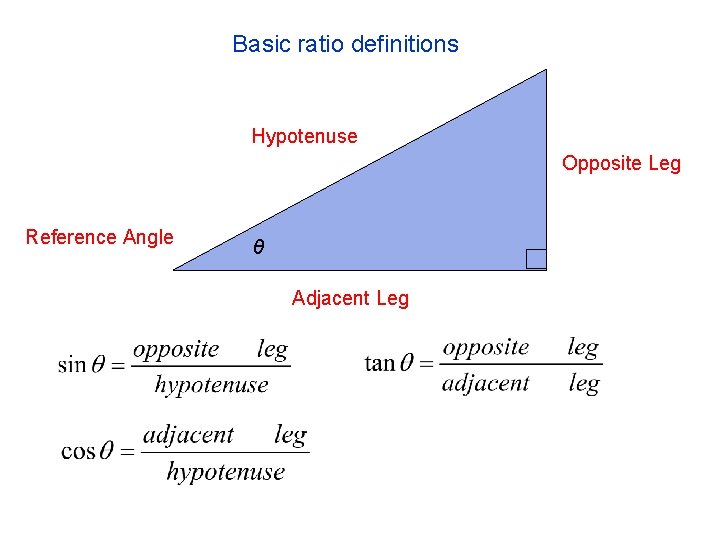
Basic ratio definitions Hypotenuse Opposite Leg Reference Angle θ Adjacent Leg

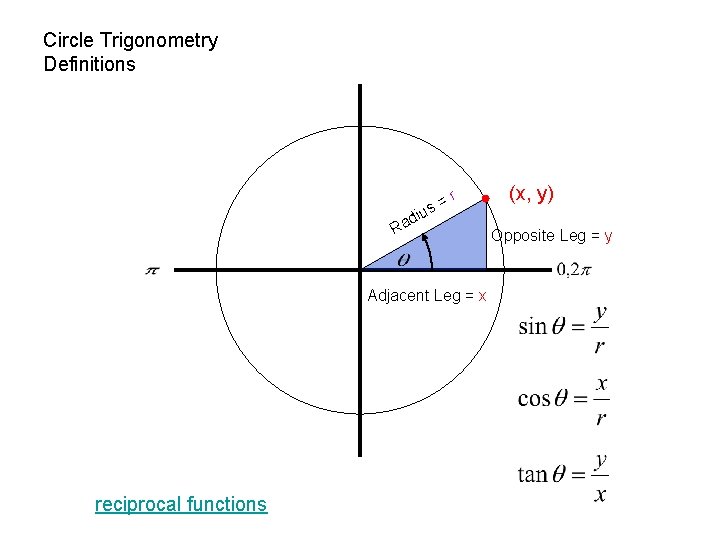
Circle Trigonometry Definitions = s u i r d Ra Adjacent Leg = x reciprocal functions (x, y) Opposite Leg = y

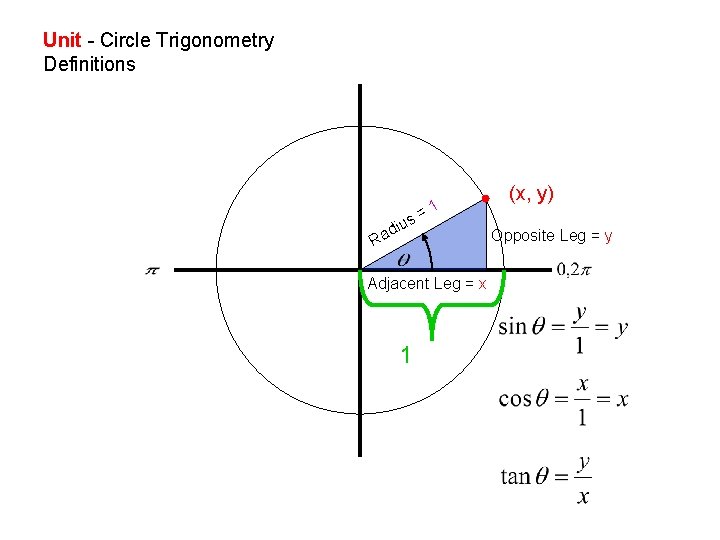
Unit - Circle Trigonometry Definitions s iu ad =1 R Adjacent Leg = x 1 (x, y) Opposite Leg = y

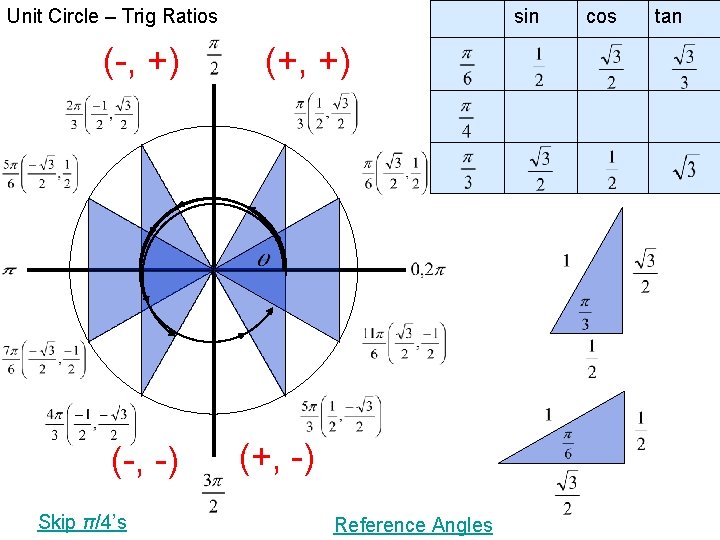
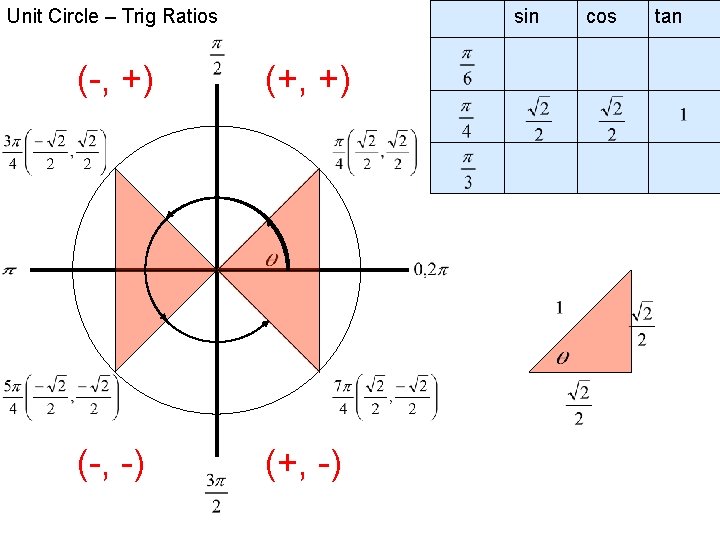
Unit Circle – Trig Ratios (-, +) (-, -) Skip π/4’s sin (+, +) (+, -) Reference Angles cos tan

Unit Circle – Trig Ratios sin (-, +) (+, +) (-, -) (+, -) cos tan

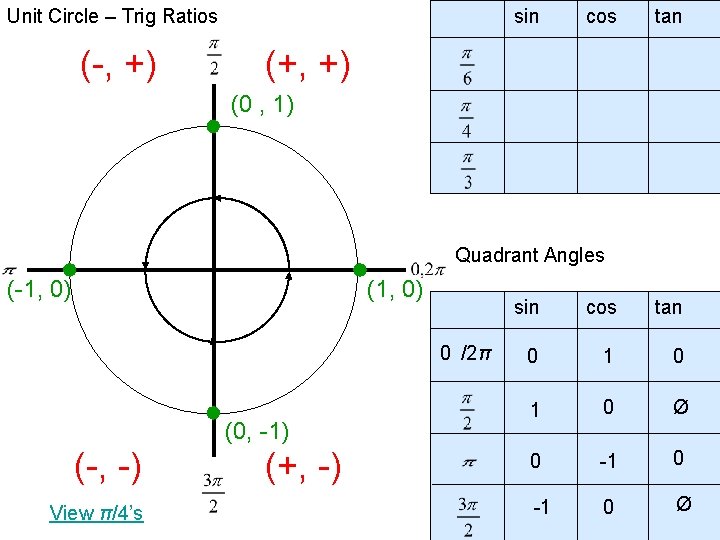
Unit Circle – Trig Ratios (-, +) sin cos tan (+, +) (0 , 1) Quadrant Angles (-1, 0) (1, 0) 0 /2π (0, -1) (-, -) View π/4’s (+, -) sin cos tan 0 1 0 Ø 0 -1 0 Ø

Unit Circle – Radian Measure (-, +) sin cos tan (+, +) Quadrant Angles 1 (-, -) (+, -) Degrees 0 /2π sin cos tan 0 1 0 Ø 0 -1 0 Ø

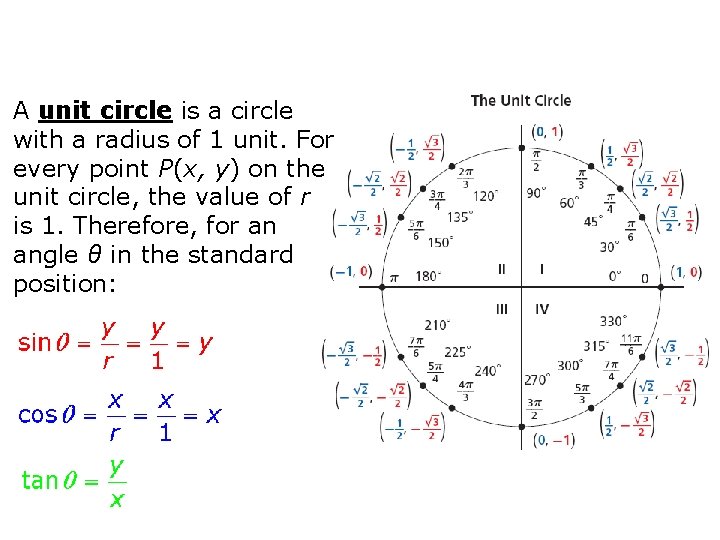
A unit circle is a circle with a radius of 1 unit. For every point P(x, y) on the unit circle, the value of r is 1. Therefore, for an angle θ in the standard position:

Graphing Trig Functions f ( x ) = A sin bx

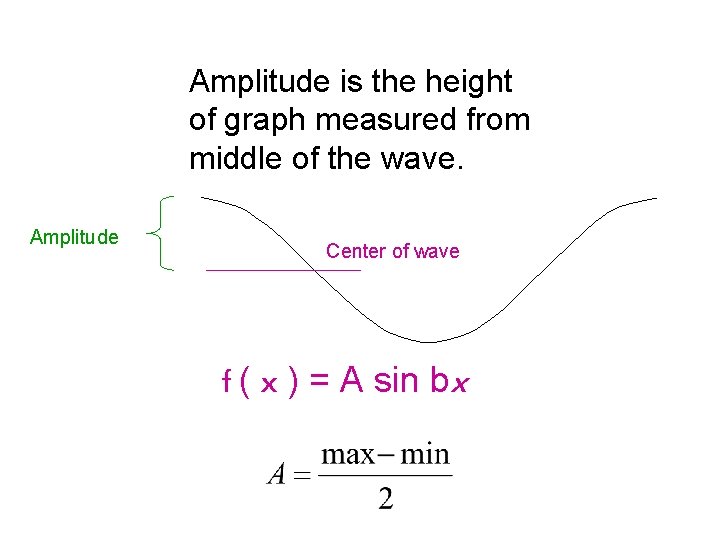
Amplitude is the height of graph measured from middle of the wave. Amplitude Center of wave f ( x ) = A sin bx

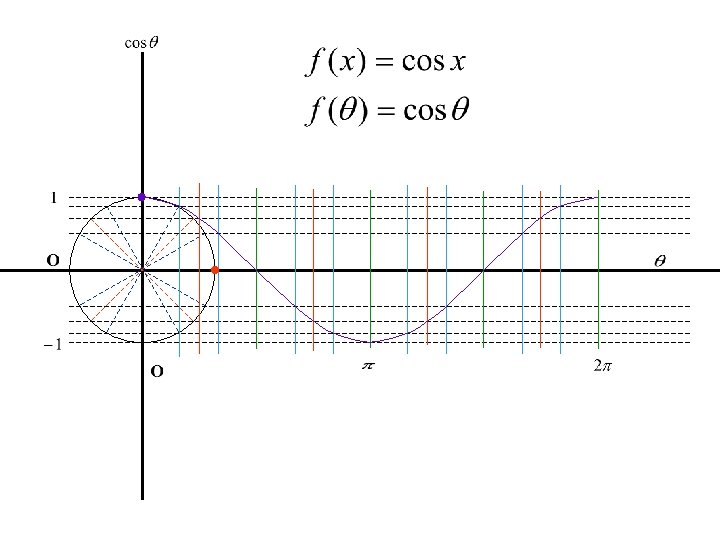
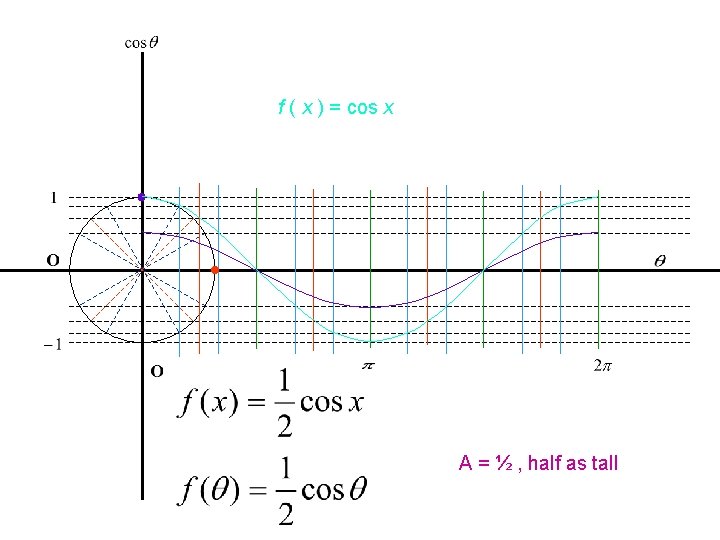
f ( x ) = cos x A = ½ , half as tall

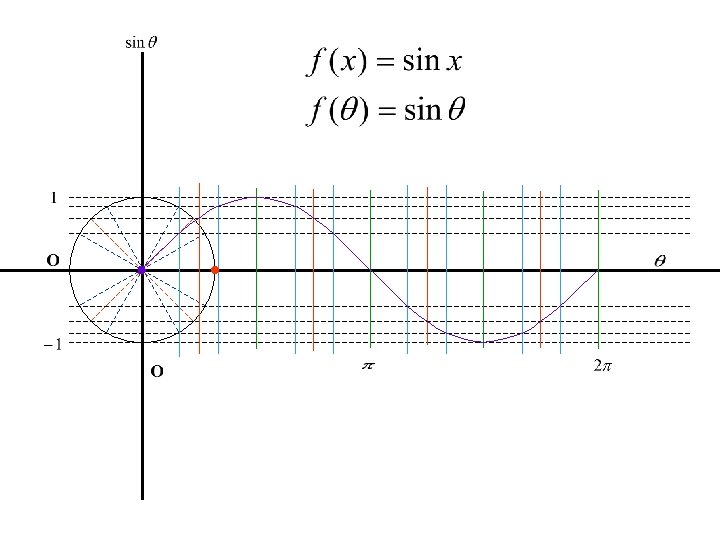
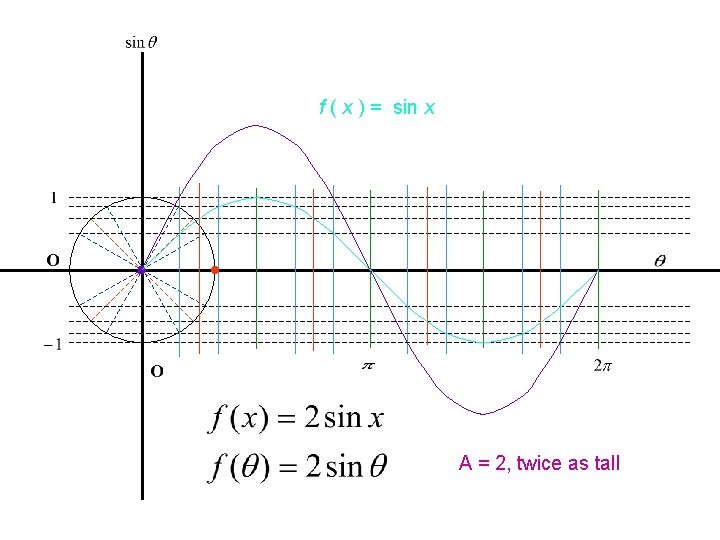
f ( x ) = sin x A = 2, twice as tall

Period of graph is distance along horizontal axis for graph to repeat (length of one cycle) f ( x ) = A sin bx

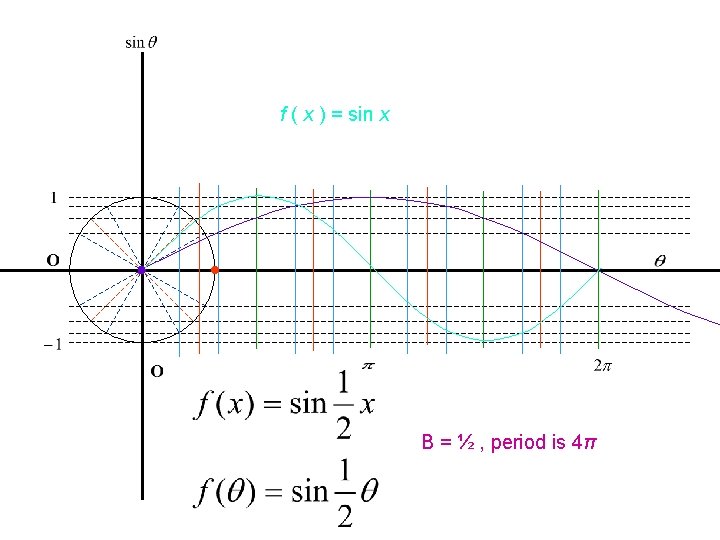
f ( x ) = sin x B = ½ , period is 4π

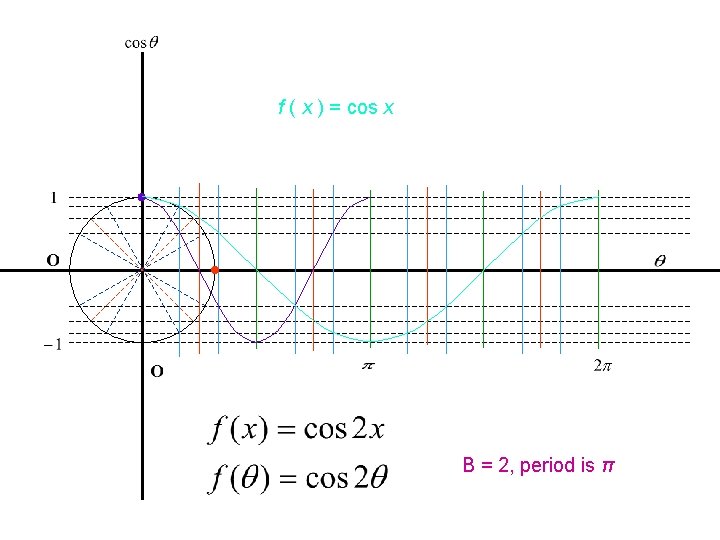
f ( x ) = cos x B = 2, period is π

Trigonometry Hipparchus, Menelaus, Ptolemy Special The Pythagoreans Graphs Right Triangles Rene’ Des. Cartes

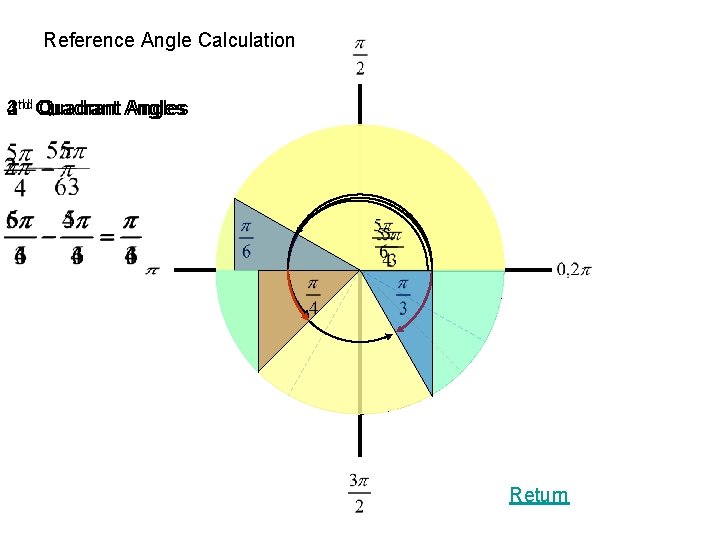
Reference Angle Calculation nd Quadrant rd 4 th 2 3 Quadrant Angles Return

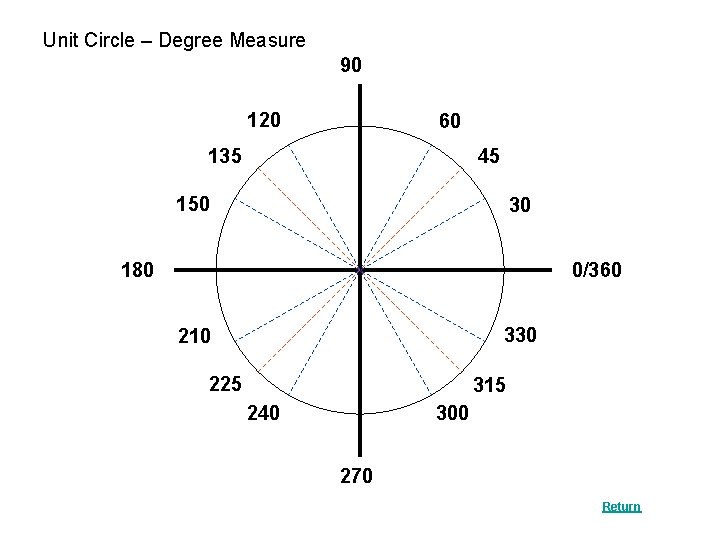
Unit Circle – Degree Measure 90 120 60 45 135 150 30 180 0/360 330 210 225 315 300 240 270 Return

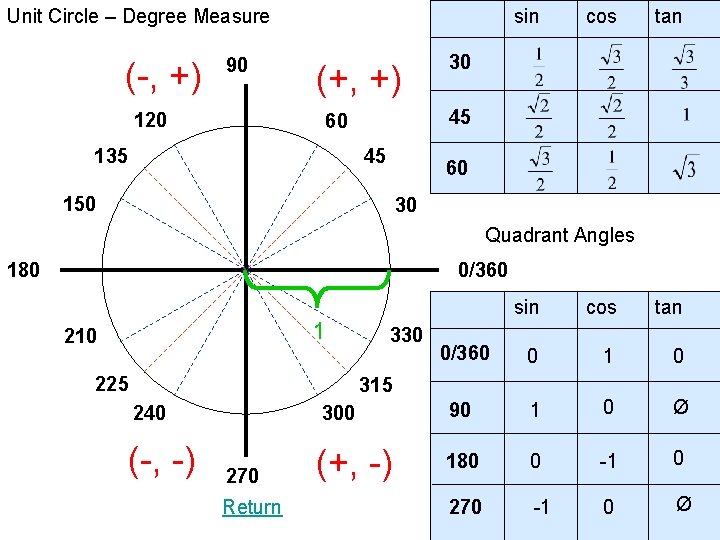
Unit Circle – Degree Measure (-, +) 90 120 sin (+, +) tan 30 45 60 45 135 cos 60 150 30 Quadrant Angles 180 0/360 1 210 225 330 sin cos tan 0/360 0 1 0 315 240 300 90 1 0 Ø (-, -) (+, -) 180 0 -1 0 270 -1 0 Ø 270 Return

Ex. # 3 Ex. # 4 Ex. # 5 Ex. # 6 return

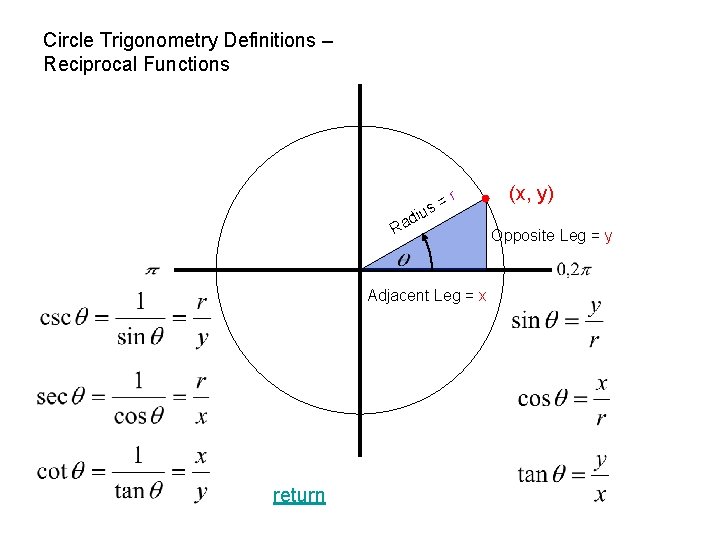
Circle Trigonometry Definitions – Reciprocal Functions = s u i r d Ra Adjacent Leg = x return (x, y) Opposite Leg = y

Unit Circle – Radian Measure 1