Trigonometry The Unit Circle The Unit Circle Imagine

Trigonometry The Unit Circle

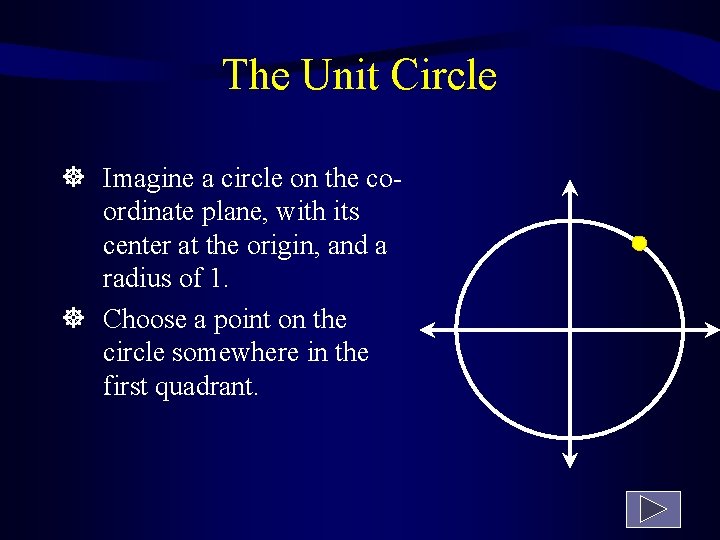
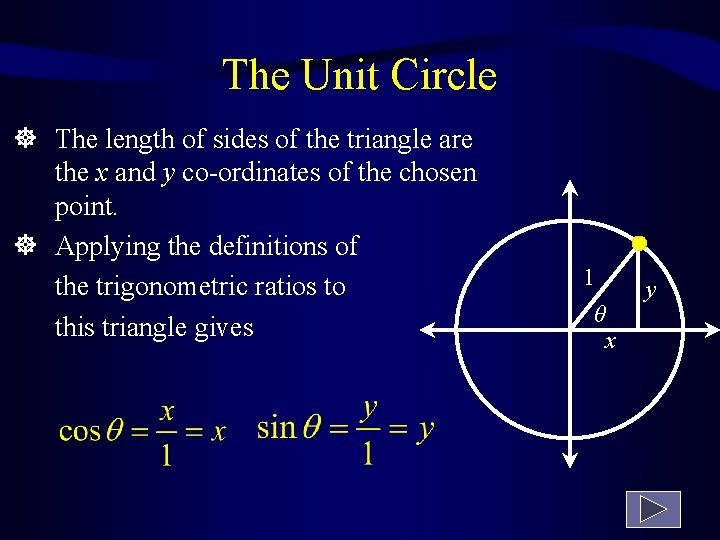
The Unit Circle Imagine a circle on the coordinate plane, with its center at the origin, and a radius of 1. Choose a point on the circle somewhere in the first quadrant.

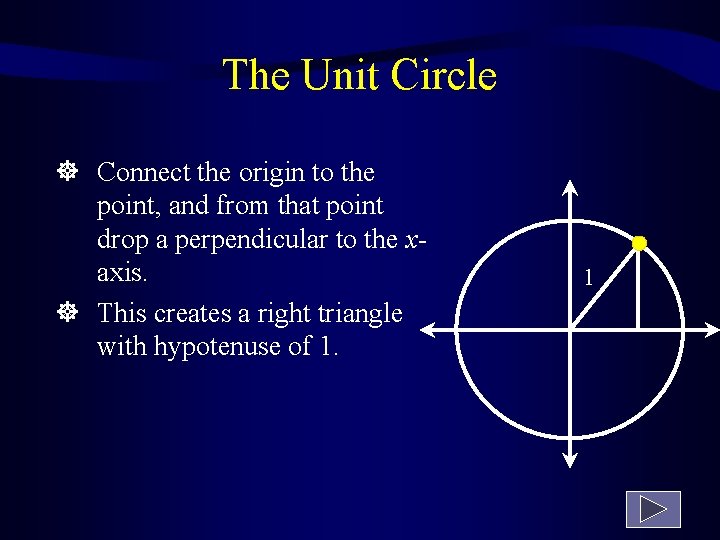
The Unit Circle Connect the origin to the point, and from that point drop a perpendicular to the xaxis. This creates a right triangle with hypotenuse of 1. 1

The Unit Circle The length of sides of the triangle are the x and y co-ordinates of the chosen point. Applying the definitions of the trigonometric ratios to this triangle gives 1 θ x y

The Unit Circle The co-ordinates of the chosen point are the cosine and sine of the angle . This provides a way to define functions sin and cos for all real numbers . The other trigonometric functions can be defined from these.

Trigonometric Functions cosecant cotan 1 θ x y

Around the Circle As that point moves around the unit circle into the second, third and fourth quadrants, the new definitions of the trigonometric functions still hold.

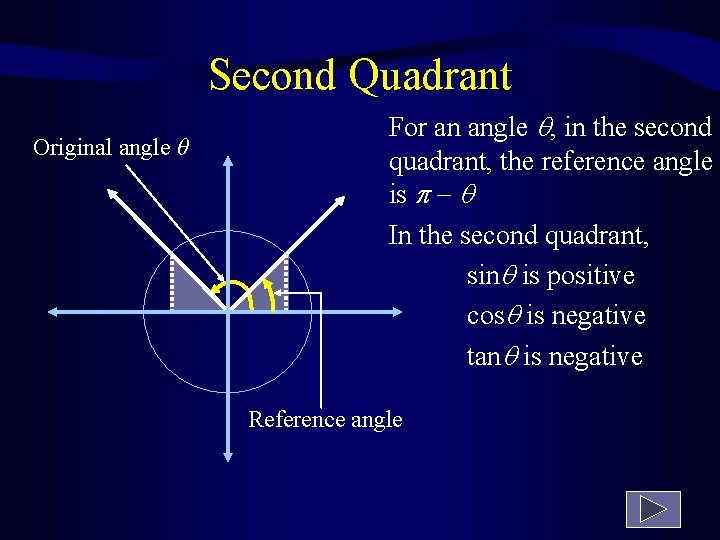
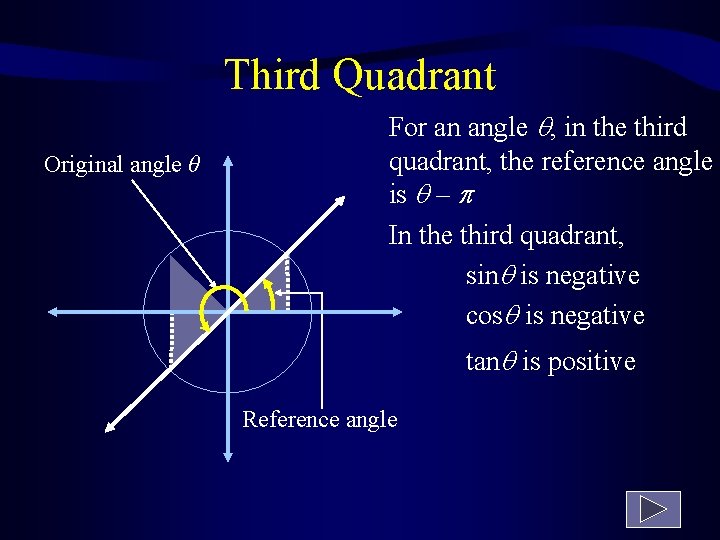
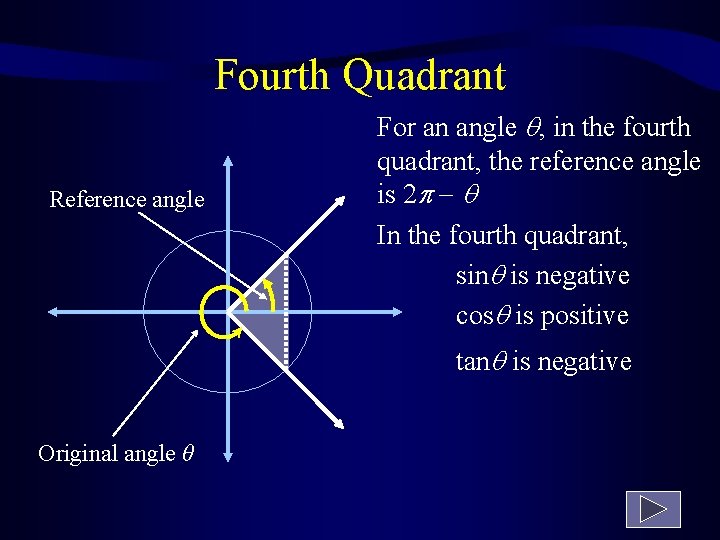
Reference Angles The angles whose terminal sides fall in the 2 nd, 3 rd, and 4 th quadrants will have values of sine, cosine and other trig functions which are identical (except for sign) to the values of angles in 1 st quadrant. The acute angle which produces the same values is called the reference angle.

Second Quadrant Original angle θ For an angle , in the second quadrant, the reference angle is In the second quadrant, sin is positive cos is negative tan is negative Reference angle

Third Quadrant Original angle θ For an angle , in the third quadrant, the reference angle is – In the third quadrant, sin is negative cos is negative tan is positive Reference angle

Fourth Quadrant Reference angle For an angle , in the fourth quadrant, the reference angle is 2 In the fourth quadrant, sin is negative cos is positive tan is negative Original angle θ

All Students Take Care Use the phrase “All Students Take Care” to remember the signs of the trigometric functions in the different quadrants. All S A T C C Students Take Care

Examples Find sin 240° in surd form. – In the 3 rd quadrant sine is negative – Find the angle to nearest x-axis Page 9 of tables 60º A T C C – Draw the angle on the unit circle S

Examples cosθ = – 0· 5. Find the two possible values of θ, where 0º ≤ θ ≤ 360°. cos. A = 0· 5 60º cos is negative in two quadrants 2 nd 180º – 60º 120º 3 rd 180º + 60º 240º S A T C