NYS COMMON CORE MATHEMATICS CURRICULUM A Story of












































- Slides: 51

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions A Close Look at Algebra II Module 2 © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM Opening Exercise © 2012 Common Core, Inc. All rights reserved. commoncore. org A Story of Functions

NYS COMMON CORE MATHEMATICS CURRICULUM Participant Poll • • • Classroom teacher Math trainer Principal or school leader District representative / leader Other © 2012 Common Core, Inc. All rights reserved. commoncore. org A Story of Functions

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Session Objectives • Experience and model the instructional approaches to teaching the content of Algebra II Module 2 lessons. • Articulate how the lessons promote mastery of the focus standards and how the module addresses the major work of the grade. • Make connections from the content of previous modules and grade levels to the content of this module. © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM Agenda • • • Overview of Module 2 Topic A Mid-Module Assessment Topic B End of Module Assessment © 2012 Common Core, Inc. All rights reserved. commoncore. org A Story of Functions

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Flow of Module 2 • 17 lessons • 7 exploration • 6 socratic • 4 problem set • 21 instructional days • Topic A: The Story of Trigonometry and Its Context • Topic B: Understanding Trigonometric Functions and Putting Them to Use © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Mathematical Themes of Module 2 • Emphasis on exploratory lessons rather than problem set lessons • Developing the sine and cosine functions through exploration of the horizontal and vertical displacement of a car on a rotating Ferris wheel • Defining sine and cosine as functions of real numbers • Graphing the sine and cosine functions and transformations of these functions • Discovering and proving trigonometric identities © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions What are students coming in with? • Experience with graphing transformations of functions on the coordinate plane (G 9) • Experience modeling data using appropriate functions (G 9 and G 11) • Experience with trigonometric ratios and circles (G 10) © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM Agenda • • • Overview of Module 2 Topic A Mid-Module Assessment Topic B End of Module Assessment © 2012 Common Core, Inc. All rights reserved. commoncore. org A Story of Functions

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Topic A: The Story of Trigonometry and Its Contexts © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lessons 1 and 2: Ferris Wheels – Tracking the Height and Co-Height of a Passenger Car • Students model the circular motion of a Ferris wheel using a paper plate. • Sine and cosine are not mentioned in these lessons. • The functions are described as the “height and co-height functions. ” • The lessons employ a familiar scenario to introduce the ideas of circular motion and periodic functions. © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lessons 1 and 2: Ferris Wheels – Tracking the Height and Co-Height of a Passenger Car PERIODIC FUNCTION. A function f whose domain is a subset of the real numbers is said to be periodic with period P if the domain of f contains x+P whenever it contains x, and if f(x+P)=f(x) for all real numbers x in its domain. If a least positive number P exists that satisfies this equation, it is called the fundamental period, or if the context is clear, just the period of the function. © 2012 Common Core, Inc. All rights reserved. commoncore. org

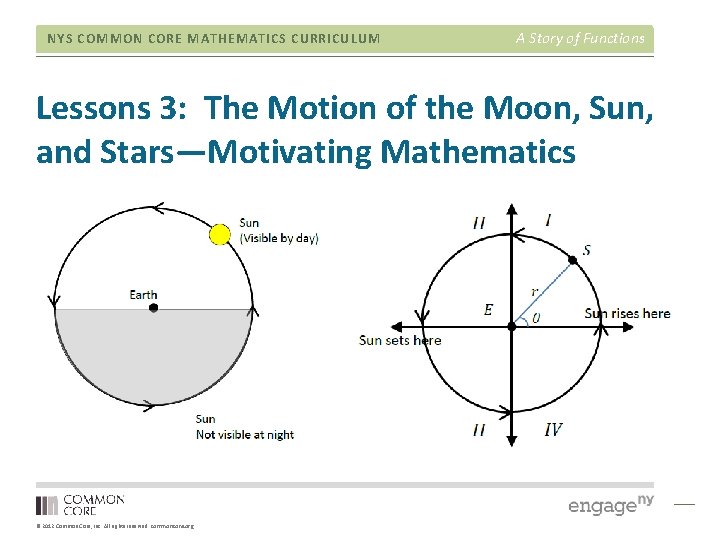
NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lessons 3: The Motion of the Moon, Sun, and Stars—Motivating Mathematics © 2012 Common Core, Inc. All rights reserved. commoncore. org

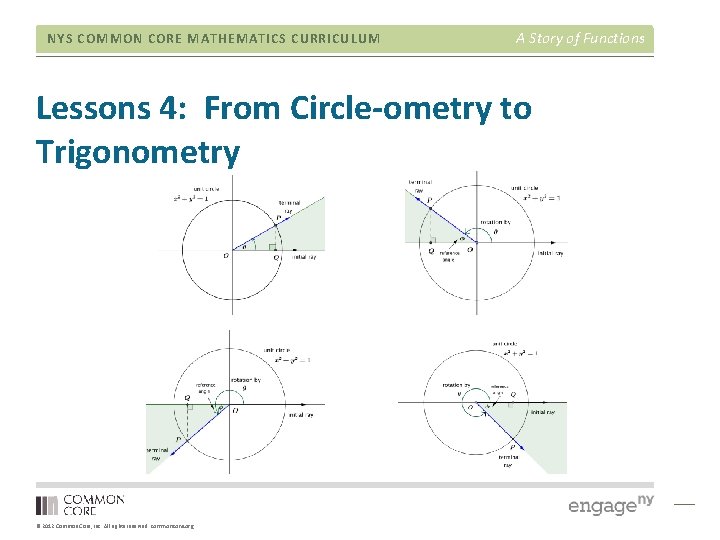
NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lessons 4: From Circle-ometry to Trigonometry • • Work example 1 and 2. Work problem set 2 – 5. Lots of information to process in this lesson. Consider using the scaffold suggestion of creating a graphic organizer. © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lessons 4: From Circle-ometry to Trigonometry © 2012 Common Core, Inc. All rights reserved. commoncore. org

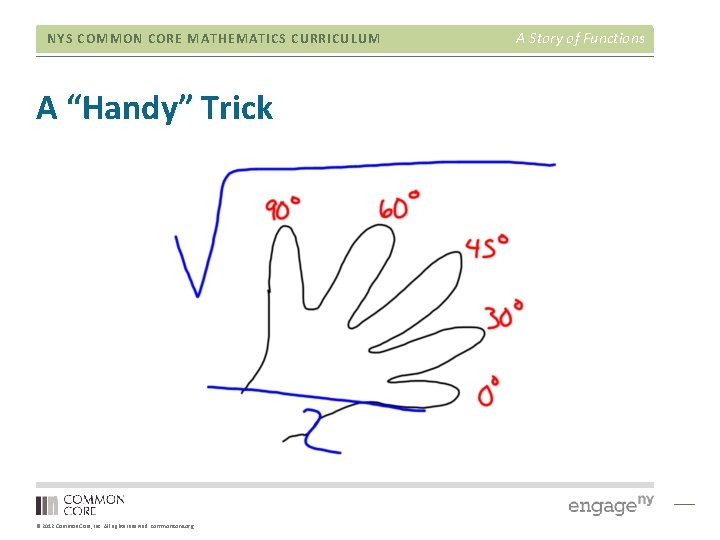
NYS COMMON CORE MATHEMATICS CURRICULUM A “Handy” Trick © 2012 Common Core, Inc. All rights reserved. commoncore. org A Story of Functions

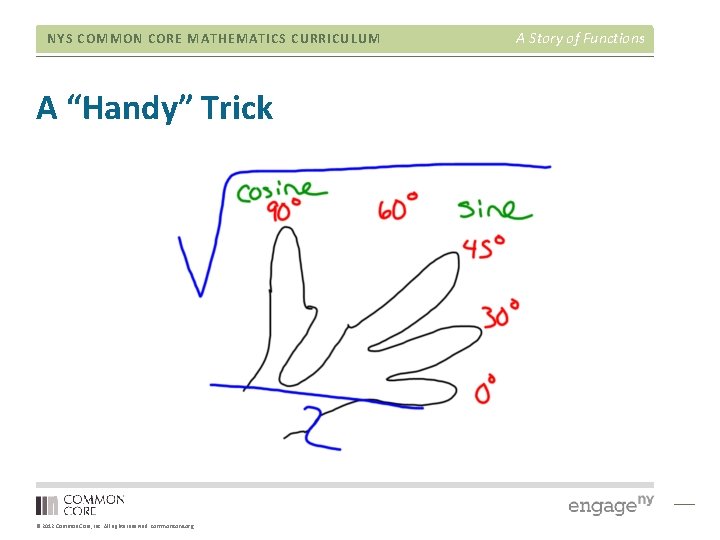
NYS COMMON CORE MATHEMATICS CURRICULUM A “Handy” Trick © 2012 Common Core, Inc. All rights reserved. commoncore. org A Story of Functions

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lessons 5: Extending the Domain of Sine and Cosine to All Real Numbers © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lesson 6: Why Call it Tangent? • Work the opening exercise. • You may need to review some terminology from geometry. © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 6: Why Call it Tangent? • Students interpret the tangent function several ways: © 2012 Common Core, Inc. All rights reserved. commoncore. org A Story of Functions

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lesson 7: Secant and the Co-Functions • What is the geometric meaning of the secant function? • Why is cosecant the reciprocal of the sine function rather than the cosine function? • How do we make sense of the domain and range of the various trigonometric functions? • Do we really need these three trigonometric functions? © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM Sprint Evaluating trigonometric functions © 2012 Common Core, Inc. All rights reserved. commoncore. org A Story of Functions

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lesson 8: Graphing the Sine and Cosine Functions • Students construct the graphs of f and g first by using the vertical and horizontal components of points on the unit circle and then by using the known values of sine and cosine. • The emphasis should be on the key features of each graph. • • Relative maxima and minima Intervals of increasing and decreasing Intercepts End behavior Symmetry Amplitude Period © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lesson 9: Awkward! Who Chose the Number 360 Anyway? • Why do we need radian measurement when degrees have worked fine up to this point? • Arc length calculations are easier for radian measurements. • When graphing sine and cosine functions, the vertical and horizontal axes must be scaled completely differently. © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lesson 9: Awkward! Who Chose the Number 360 Anyway? • The main reason that we see the transition from degrees to radians is that all trigonometry done in Calculus is based on radian measurement. • Find . • In Calculus, the fact that Is used to derive the fact that the derivative of sin(x) is cos(x) when we measure x in radians. © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lesson 9: Awkward! Who Chose the Number 360 Anyway? © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lesson 9: Awkward! Who Chose the Number 360 Anyway? © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lesson 10: Basic Trigonometric Identities from Graphs • Students use the graphs of the sine and cosine functions to note properties that lead to trigonometric identities. • Periodicity • Symmetry (even/odd functions) • Horizontal translations • Note that an identity is a statement that two functions are equal on a common domain. • The statement “sin(x+2π)=sin(x)” itself is not an identity. • The correct statement is “sin(x+2π)=sin(x) for all real numbers x. ” © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lesson 10: Basic Trigonometric Identities from Graphs • Key takeaways from this lesson: • The basic trigonometric identities derived from the periodic nature and symmetry of the graphs of each function. • For all real numbers x, • The graphs of sine and cosine can be made to coincide with one another by using horizontal shifts. • For all real numbers x, © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Key Points – Topic A • There is a rich historical context that motivates the study of trigonometry. • Students are given opportunities to explore the meaning of the trigonometric functions and their properties in order to develop a deeper understanding. • Students make connections between the values of sine and cosine for particular amounts of rotation with the graphs of the functions and then to trigonometric identities. © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM Agenda • • • Overview of Module 2 Topic A Mid-Module Assessment Topic B End of Module Assessment © 2012 Common Core, Inc. All rights reserved. commoncore. org A Story of Functions

NYS COMMON CORE MATHEMATICS CURRICULUM Mid-Module Assessment Work with a partner on this assessment © 2012 Common Core, Inc. All rights reserved. commoncore. org A Story of Functions

NYS COMMON CORE MATHEMATICS CURRICULUM Scoring the Assessment © 2012 Common Core, Inc. All rights reserved. commoncore. org A Story of Functions

NYS COMMON CORE MATHEMATICS CURRICULUM Agenda • • • Overview of Module 2 Topic A Mid-Module Assessment Topic B End of Module Assessment © 2012 Common Core, Inc. All rights reserved. commoncore. org A Story of Functions

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Topic B: Understanding Trigonometric Functions and Putting Them to Use • Students use trigonometric functions to model periodic behavior. • The concept of polynomial identities covered in module 1 is extended to trigonometric identities. • Continue to emphasize the proper statement of a trigonometric identity as the pairing of a statement that two functions are equivalent on a given domain and an identification of that domain. © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lesson 11: Transforming the Graph of the Sine Function © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lesson 11: Transforming the Graph of the Sine Function © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lesson 12: Ferris Wheels—Using Trigonometric Functions to Model Cyclical Behavior © 2012 Common Core, Inc. All rights reserved. commoncore. org

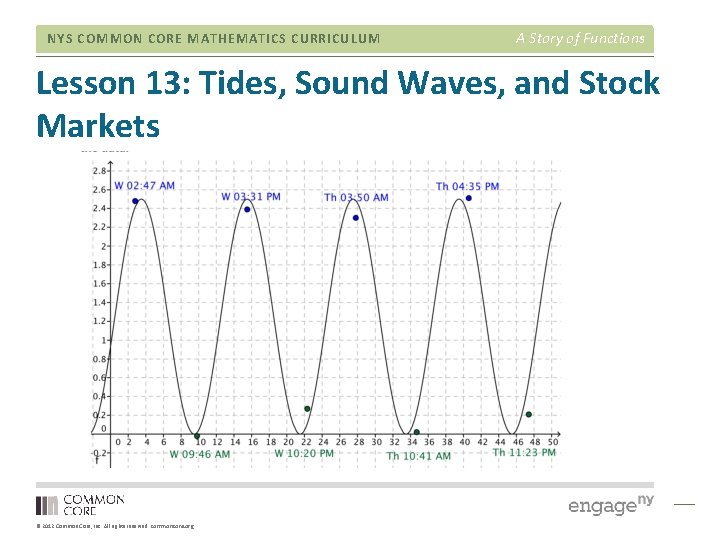
NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lesson 13: Tides, Sound Waves, and Stock Markets © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lesson 14: Graphing the Tangent Function © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lesson 14: Graphing the Tangent Function • At this point, it would be valuable to compare identities developed throughout this module. © 2012 Common Core, Inc. All rights reserved. commoncore. org

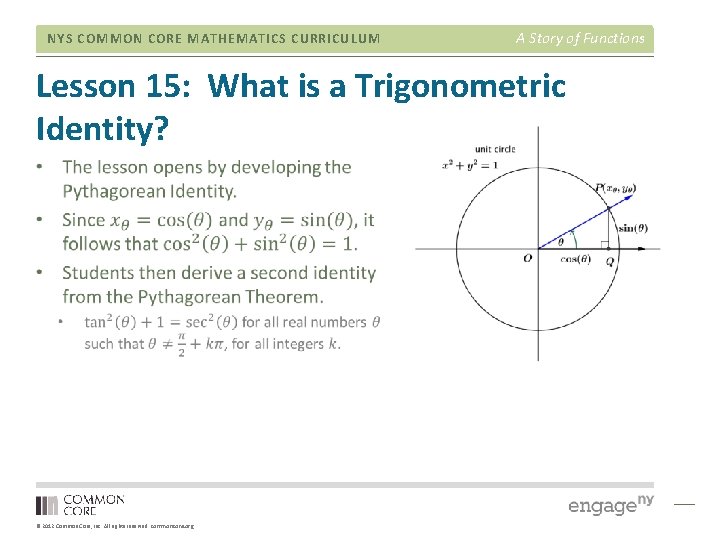
NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lesson 15: What is a Trigonometric Identity? © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lesson 16: Proving Trigonometric Identities © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Lesson 17: Trigonometric Identity Proofs © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Key Points – Topic B • Trigonometric functions are useful for modeling periodic data. • A trigonometric identity is a statement that two functions are equivalent on a given domain and an identification of that domain. • Trigonometric identities can be proven graphically, numerically, and algebraically. © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM Key Points – Module 2 Lessons © 2012 Common Core, Inc. All rights reserved. commoncore. org A Story of Functions

NYS COMMON CORE MATHEMATICS CURRICULUM Agenda • • • Overview of Module 2 Topic A Mid-Module Assessment Topic B End of Module Assessment © 2012 Common Core, Inc. All rights reserved. commoncore. org A Story of Functions

NYS COMMON CORE MATHEMATICS CURRICULUM End-of-Module Assessment Work with a partner on this assessment © 2012 Common Core, Inc. All rights reserved. commoncore. org A Story of Functions

NYS COMMON CORE MATHEMATICS CURRICULUM Scoring the Assessment © 2012 Common Core, Inc. All rights reserved. commoncore. org A Story of Functions

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Key Points – End-of-Module Assessment • End of Module assessment are designed to assess all standards of the module (at least at the cluster level) with an emphasis on assessing thoroughly those presented in the second half of the module. • Recall, as much as possible, assessment items are designed to asses the standards while emulating PARCC Type 2 and Type 3 tasks. • Recall, rubrics are designed to inform each district / school / teacher as they make decisions about the use of assessments in the assignment of grades. © 2012 Common Core, Inc. All rights reserved. commoncore. org

NYS COMMON CORE MATHEMATICS CURRICULUM A Story of Functions Biggest Takeaway What are your biggest takeaways from the study of Module 2? How can you support successful implementation of these materials at your schools given your role as a teacher, trainer, school or district leader, administrator or other representative? © 2012 Common Core, Inc. All rights reserved. commoncore. org