Introduction A unit circle is a circle that

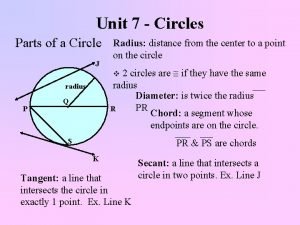
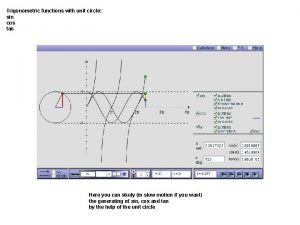
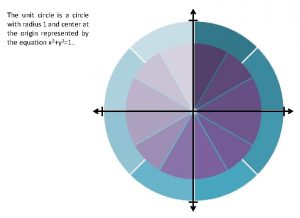
Introduction A unit circle is a circle that has a radius of 1 unit, with the center of the circle located at the origin of the coordinate plane. Because r = 1 in the unit circle, it can be a useful tool for discussing arc lengths and angles in circles. An angle in a unit circle can be studied in radians or degrees; however, since radians directly relate an angle measure to an arc length, radian measures are more useful in calculations. 1 5. 1. 2: The Unit Circle

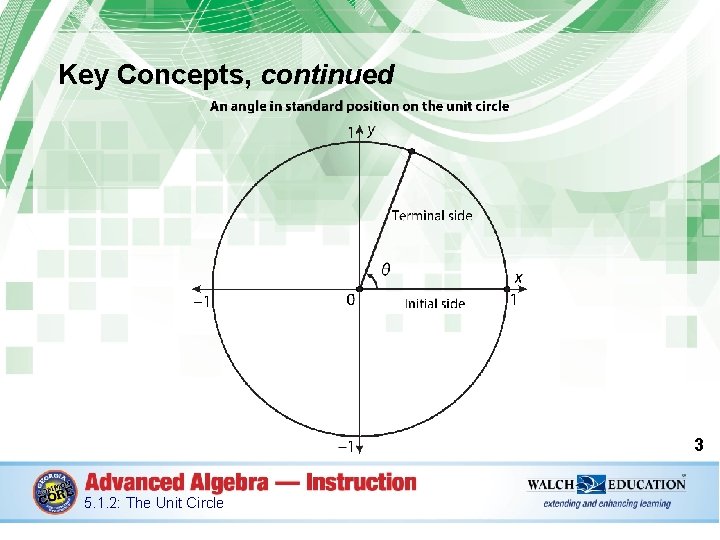
Key Concepts • Angles are typically in standard position on a unit circle. This means that the center of the circle is placed at the origin of the coordinate plane, and the vertex of the angle is on the origin at the center of the circle. The initial side of the angle (the stationary ray from which the measurement of the angle starts) is located along the positive x-axis. The terminal side (the movable ray that determines the measure of the angle) may be in any location. 2 5. 1. 2: The Unit Circle

Key Concepts, continued 3 5. 1. 2: The Unit Circle

Key Concepts, continued • The terminal side of the angle may be rotated counterclockwise to create a positive angle or clockwise to create a negative angle. • To sketch an angle in radians on the unit circle, remember that halfway around the circle (180°) is equal to π radians and that a full rotation (360°) is equal to 2π radians. Then use the fraction of π to estimate the angle’s location, if it falls somewhere between these measures. 4 5. 1. 2: The Unit Circle

Key Concepts, continued • Within the unit circle, each angle has a reference angle. The reference angle is always the angle that the terminal side makes with the x-axis. The reference angle’s sine, cosine, and tangent are the same as that of the original angle except for the sign, which is based on the quadrant in which the terminal side is located. 5 5. 1. 2: The Unit Circle

Key Concepts, continued • Recall that a right triangle has one right angle and two acute angles (less than 90°). Sine, cosine, and tangent are trigonometric functions of an acute angle θ in a right triangle and are determined by the ratios of the lengths of the opposite side, adjacent side, and the hypotenuse of that triangle, summarized as follows. 6 5. 1. 2: The Unit Circle

Key Concepts, continued • The sine of θ = sin θ = • The cosine of θ = cos θ = • The tangent of θ = tan θ = 7 5. 1. 2: The Unit Circle

Key Concepts, continued • To find a reference angle, first sketch the original angle to determine which quadrant it lies in. Then, determine the measure of the angle between the terminal side and the x-axis. The following table shows the relationships between the reference angle and the original angle (θ ) for each quadrant. Quadrant Reference angle (degrees) Reference angle (radians) I same as θ II 180° – θ π radians – θ III θ – 180° θ – π radians IV 360° – θ 2π radians – θ 5. 1. 2: The Unit Circle 8

Key Concepts, continued • If an angle is larger than 2π radians (360°), subtract a full rotation (2π radians or 360°) until the angle is less than 2π radians (360°). Then, find the reference angle of the resulting angle. • The coordinates of the point at which the terminal side intersects the unit circle are always given by (cos θ , sin θ ), where θ is the measure of the angle. 9 5. 1. 2: The Unit Circle

Common Errors/Misconceptions • mistakenly thinking that the reference angle in Quadrants II and IV is the angle that the terminal side makes with the y-axis • reversing sin θ and cos θ when attempting to find the coordinates of the point where the terminal side intersects the unit circle 10 5. 1. 2: The Unit Circle

Guided Practice Example 1 On a unit circle, sketch angles that measure radians, radian, and radians. 11 5. 1. 2: The Unit Circle

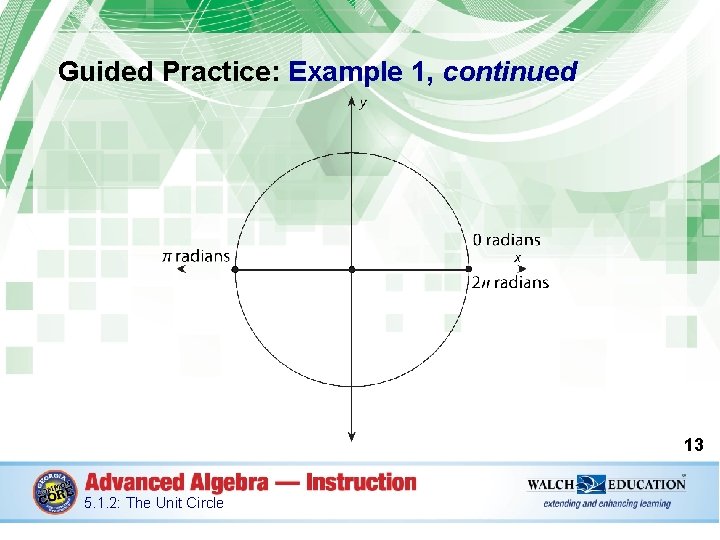
Guided Practice: Example 1, continued 1. Sketch a unit circle, then label π radians and 2π radians. A half rotation (180°) is π radians and a full rotation (360°) is 2π radians. Notice that 0 radians and 2π radians are in the same location on the unit circle, but represent different angle measures. 12 5. 1. 2: The Unit Circle

Guided Practice: Example 1, continued 13 5. 1. 2: The Unit Circle

Guided Practice: Example 1, continued 2. Sketch radians. is the same as . In other words, the terminal side is of the way between 0 and π. Thus, imagine the semicircle between 0 radians and π radians split into thirds, and then sketch the angle of the way around the semicircle. 14 5. 1. 2: The Unit Circle

Guided Practice: Example 1, continued 15 5. 1. 2: The Unit Circle

Guided Practice: Example 1, continued 3. Sketch radian. is the same as . In other words, it is of the way to π. Thus, imagine the semicircle between 0 radians and π radians split into fourths, and then sketch the angle of the way around the semicircle. 16 5. 1. 2: The Unit Circle

Guided Practice: Example 1, continued 17 5. 1. 2: The Unit Circle

Guided Practice: Example 1, continued 4. Sketch radians. is the same as which is equal to Because this value is greater than π, it goes beyond π radians. It is of the way past π. Imagine the semicircle between π radians and 2π radians split into sevenths, and then sketch the angle of the way around the semicircle. 18 5. 1. 2: The Unit Circle

Guided Practice: Example 1, continued 19 5. 1. 2: The Unit Circle

Guided Practice: Example 1, continued 5. Summarize your findings. The diagram on the next slide shows the final unit circle with angles that measure radians, radian, and radians. 20 5. 1. 2: The Unit Circle

Guided Practice: Example 1, continued ✔ 21 5. 1. 2: The Unit Circle

Guided Practice: Example 1, continued 22 5. 1. 2: The Unit Circle

Guided Practice Example 2 Find the reference angles for angles that measure radians, and 5. 895 radians. 23 5. 1. 2: The Unit Circle

Guided Practice: Example 2, continued 1. Sketch an angle with a measure of radians on the unit circle. radians is the same as radians; therefore, this angle will be of the way between π radians and 2π radians. 24 5. 1. 2: The Unit Circle

Guided Practice: Example 2, continued 25 5. 1. 2: The Unit Circle

Guided Practice: Example 2, continued 2. Determine the measure of the angle between the terminal side and the x-axis. Since the terminal side falls in Quadrant III, subtract π radians from the original angle measure, radians, to find the measure of the reference angle. 26 5. 1. 2: The Unit Circle

Guided Practice: Example 2, continued Subtract π from the original angle measure. Rewrite π as a fraction with a common denominator. Subtract. The reference angle for radians is radians. 27 5. 1. 2: The Unit Circle

Guided Practice: Example 2, continued 3. Sketch radians. Sketch radians of the way between 0 and π radians. 28 5. 1. 2: The Unit Circle

Guided Practice: Example 2, continued 29 5. 1. 2: The Unit Circle

Guided Practice: Example 2, continued 4. Determine the measure of the angle between the terminal side and the x-axis. Since the terminal side falls in Quadrant II, subtract radians from π radians to find the measure of the reference angle. 30 5. 1. 2: The Unit Circle

Guided Practice: Example 2, continued Subtract the original angle measure from π. Rewrite π as a fraction with a common denominator. Subtract. The reference angle for radians is radians. 31 5. 1. 2: The Unit Circle

Guided Practice: Example 2, continued 5. Sketch 5. 895 radians. Since π is not included in this measurement, we must use decimal approximations. π is approximately 3. 14 and 2π is approximately 6. 28. 5. 895 is fairly close to 6. 28 and thus will fall in Quadrant IV. 32 5. 1. 2: The Unit Circle

Guided Practice: Example 2, continued 33 5. 1. 2: The Unit Circle

Guided Practice: Example 2, continued 6. Determine the measure of the angle between the terminal side and the x-axis. Since the terminal side falls in Quadrant IV, subtract 5. 895 radians from 2π radians to find a more precise measure of the reference angle. 2π – 5. 895 ≈ 0. 388 The measure of the reference angle for 5. 895 radians is approximately 0. 388 radian. ✔ 34 5. 1. 2: The Unit Circle

Guided Practice: Example 2, continued Applet A Applet B 35 5. 1. 2: The Unit Circle