Unit Circle and Radians Unit 3 Radians l




![Arc Length l Theorem. [Arc Length] For a circle of radius r, a central Arc Length l Theorem. [Arc Length] For a circle of radius r, a central](https://slidetodoc.com/presentation_image_h2/70ef81d09aa3c1d06707c9c09ec54632/image-5.jpg)




![Area of a Sector of a Circle l Theorem. [Area of a Sector] The Area of a Sector of a Circle l Theorem. [Area of a Sector] The](https://slidetodoc.com/presentation_image_h2/70ef81d09aa3c1d06707c9c09ec54632/image-10.jpg)
































![Ranges of Trigonometric Functions l Sine and cosine have range [{1, 1] {1 · Ranges of Trigonometric Functions l Sine and cosine have range [{1, 1] {1 ·](https://slidetodoc.com/presentation_image_h2/70ef81d09aa3c1d06707c9c09ec54632/image-44.jpg)












![Even-Odd Properties l Theorem. [Even-Odd Properties] sin({µ) = {sin(µ) cos({µ) = cos(µ) tan({µ) = Even-Odd Properties l Theorem. [Even-Odd Properties] sin({µ) = {sin(µ) cos({µ) = cos(µ) tan({µ) =](https://slidetodoc.com/presentation_image_h2/70ef81d09aa3c1d06707c9c09ec54632/image-57.jpg)





![Properties of the Sine Function l Domain: All real numbers l Range: [{1, 1] Properties of the Sine Function l Domain: All real numbers l Range: [{1, 1]](https://slidetodoc.com/presentation_image_h2/70ef81d09aa3c1d06707c9c09ec54632/image-64.jpg)
![Properties of the Cosine Function l Domain: All real numbers l Range: [{1, 1] Properties of the Cosine Function l Domain: All real numbers l Range: [{1, 1]](https://slidetodoc.com/presentation_image_h2/70ef81d09aa3c1d06707c9c09ec54632/image-67.jpg)











![Graphing the Cotangent Function l Periodicity: Only need to graph on interval [0, ¼] Graphing the Cotangent Function l Periodicity: Only need to graph on interval [0, ¼]](https://slidetodoc.com/presentation_image_h2/70ef81d09aa3c1d06707c9c09ec54632/image-86.jpg)










- Slides: 98

Unit Circle and Radians Unit 3

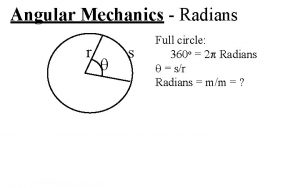
Radians l Central angle: An angle whose vertex is at the center of a circle l Central angles subtend an arc on the circle

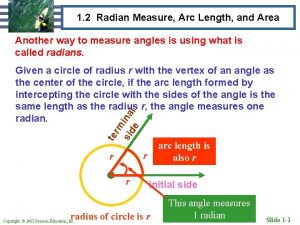
Radians l One radian is the measure of an angle which subtends an arc with length equal to the radius of the circle

Radians IMPORTANT! Radians are dimensionless l If an angle appears with no units, it must be assumed to be in radians l
![Arc Length l Theorem Arc Length For a circle of radius r a central Arc Length l Theorem. [Arc Length] For a circle of radius r, a central](https://slidetodoc.com/presentation_image_h2/70ef81d09aa3c1d06707c9c09ec54632/image-5.jpg)
Arc Length l Theorem. [Arc Length] For a circle of radius r, a central angle of µ radians subtends an arc whose length s is s = rµ WARNING! l The angle must be given in radians

Arc Length l Example. Problem: Find the length of the arc of a circle of radius 5 centimeters subtended by a central angle of 1. 4 radians Answer:

Radians vs. Degrees l 1 revolution = 2¼ radians = 360± l l l 180± = ¼ radians 1± = radians 1 radian =

Radians vs. Degrees l Example. Convert each angle in degrees to radians and each angle in radians to degrees (a) Problem: 45± Answer: (b) Problem: {270± Answer: (c) Problem: 2 radians Answer:

Radians vs. Degrees l Measurements of common angles
![Area of a Sector of a Circle l Theorem Area of a Sector The Area of a Sector of a Circle l Theorem. [Area of a Sector] The](https://slidetodoc.com/presentation_image_h2/70ef81d09aa3c1d06707c9c09ec54632/image-10.jpg)
Area of a Sector of a Circle l Theorem. [Area of a Sector] The area A of the sector of a circle of radius r formed by a central angle of µ radians is

Area of a Sector of a Circle l Example. Problem: Find the area of the sector of a circle of radius 3 meters formed by an angle of 45±. Round your answer to two decimal places. Answer: WARNING! l The angle again must be given in radians

Linear and Angular Speed l Object moving around a circle or radius r at a constant speed l Linear speed: Distance traveled divided by elapsed time t = time µ = central angle swept out in time t s = rµ = arc length = distance traveled

Linear and Angular Speed l Object moving around a circle or radius r at a constant speed l l Angular speed: Angle swept out divided by elapsed time Linear and angular speeds are related v = r!

Linear and Angular Speed l Example. A neighborhood carnival has a Ferris wheel whose radius is 50 feet. You measure the time it takes for one revolution to be 90 seconds. (a) Problem: What is the linear speed (in feet per second) of this Ferris wheel? Answer: (b) Problem: What is the angular speed (in radians per second)? Answer:

Key Points l l l l Basic Terminology Measuring Angles Degrees, Minutes and Seconds Radians Arc Length Radians vs. Degrees Area of a Sector of a Circle Linear and Angular Speed

Trigonometric Functions: Unit Circle Approach Section 5. 2

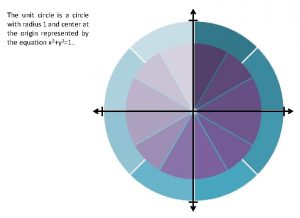
Unit Circle l Unit circle: Circle with radius 1 centered at the origin Equation: x 2 + y 2 = 1 l Circumference: 2¼ l

Unit Circle l Travel t units around circle, starting from the point (1, 0), ending at the point P = (x, y) l The point P = (x, y) is used to define the trigonometric functions of t

Trigonometric Functions l Let t be a real number and P = (x, y) the point on the unit circle corresponding to t: Sine function: y-coordinate of P sin t = y l Cosine function: x-coordinate of P cos t = x l Tangent function: if x 0 l

Trigonometric Functions l Let t be a real number and P = (x, y) the point on the unit circle corresponding to t: l Cosecant function: if y 0 l Secant function: if x 0 l Cotangent function: if y 0

Exact Values Using Points on the Circle l l A point on the unit circle will satisfy the equation x 2 + y 2 = 1 Use this information together with the definitions of the trigonometric functions.

Exact Values Using Points on the Circle l Example. Let t be a real number and P= the point on the unit circle that corresponds to t. Problem: Find the values of sin t, cos t, tan t, csc t, sec t and cot t Answer:

Trigonometric Functions of Angles l l Convert between arc length and angles on unit circle Use angle µ to define trigonometric functions of the angle µ

Exact Values for Quadrantal Angles l Quadrantal angles correspond to integer multiples of 90± or of radians

Exact Values for Quadrantal Angles l Example. Find the values of the trigonometric functions of µ Problem: µ = 0± Answer:

Exact Values for Quadrantal Angles l Example. Find the values of the trigonometric functions of µ Problem: µ = Answer: = 90±

Exact Values for Quadrantal Angles l Example. Find the values of the trigonometric functions of µ Problem: µ = ¼ = 180± Answer:

Exact Values for Quadrantal Angles l Example. Find the values of the trigonometric functions of µ Problem: µ = Answer: = 270±

Exact Values for Quadrantal Angles

Exact Values for Quadrantal Angles l Example. Find the exact values of (a) Problem: sin({90±) Answer: (b) Problem: cos(5¼) Answer:

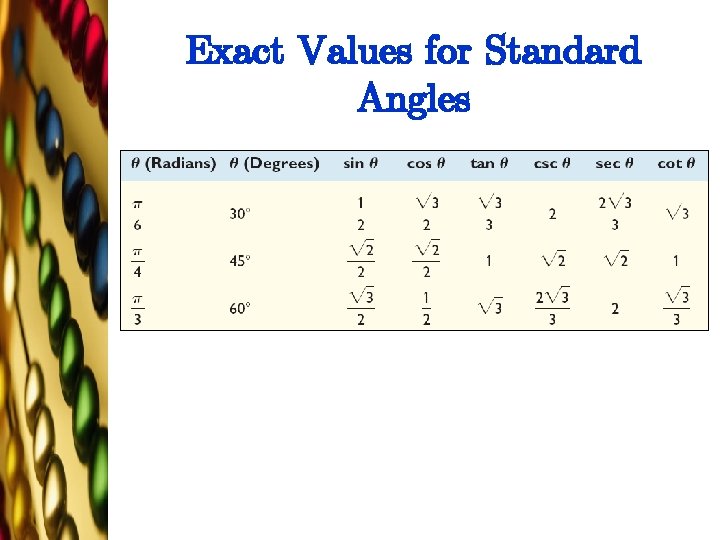
Exact Values for Standard Angles l Example. Find the values of the trigonometric functions of µ Problem: µ = Answer: = 45±

Exact Values for Standard Angles l Example. Find the values of the trigonometric functions of µ Problem: µ = Answer: = 60±

Exact Values for Standard Angles l Example. Find the values of the trigonometric functions of µ Problem: µ = Answer: = 30±

Exact Values for Standard Angles

Exact Values for Standard Angles l Example. Find the values of the following expressions (a) Problem: sin(315±) Answer: (b) Problem: cos({120±) Answer: (c) Problem: Answer:

Approximating Values Using a Calculator IMPORTANT! l l Be sure that your calculator is in the correct mode. Use the basic trigonometric facts:

Approximating Values Using a Calculator l Example. Use a calculator to find the approximate values of the following. Express your answers rounded to two decimal places. (a) Problem: sin 57± Answer: (b) Problem: cot {153± Answer: (c) Problem: sec 2 Answer:

Circles of Radius r l Theorem. For an angle µ in standard position, let P = (x, y) be the point on the terminal side of µ that is also on the circle x 2 + y 2 = r 2. Then

Circles of Radius r l Example. Problem: Find the exact values of each of the trigonometric functions of an angle µ if ({12, {5) is a point on its terminal side. Answer:

Key Points l l l l Unit Circle Trigonometric Functions Exact Values Using Points on the Circle Trigonometric Functions of Angles Exact Values for Quadrantal Angles Exact Values for Standard Angles Approximating Values Using a Calculator

Key Points (cont. ) l Circles of Radius r

Properties of the Trigonometric Functions Section 5. 3

Domains of Trigonometric Functions l l l Domain of sine and cosine functions is the set of all real numbers Domain of tangent and secant functions is the set of all real numbers, except odd integer multiples of = 90± Domain of cotangent and cosecant functions is the set of all real numbers, except integer multiples of ¼ = 180±
![Ranges of Trigonometric Functions l Sine and cosine have range 1 1 1 Ranges of Trigonometric Functions l Sine and cosine have range [{1, 1] {1 ·](https://slidetodoc.com/presentation_image_h2/70ef81d09aa3c1d06707c9c09ec54632/image-44.jpg)
Ranges of Trigonometric Functions l Sine and cosine have range [{1, 1] {1 · sin µ · 1; jsin µj · 1 l {1 · cos µ · 1; jcos µj · 1 l l Range of cosecant and secant is ({1, {1] [ [1, 1) jcsc µj ¸ 1 l jsec µj ¸ 1 l l Range of tangent and cotangent functions is the set of all real numbers

Periods of Trigonometric Functions l l Periodic function: A function f with a positive number p such that whenever µ is in the domain of f, so is µ + p, and f(µ + p) = f(µ) (Fundamental) period of f: smallest such number p, if it exists

Periods of Trigonometric Functions l Periodic Properties: sin(µ + 2¼) = sin µ cos(µ + 2¼) = cos µ tan(µ + ¼) = tan µ csc(µ + 2¼) = csc µ sec(µ + 2¼) = sec µ cot(µ + ¼) = cot µ l l Sine, cosecant and secant have period 2¼ Tangent and cotangent have period ¼

Periods of Trigonometric Functions l Example. Find the exact values of (a) Problem: sin(7¼) Answer: (b) Problem: Answer: (c) Problem: Answer:

Signs of the Trigonometric Functions l P = (x, y) corresponding to angle µ l l Definitions of functions, where defined Find the signs of the functions Quadrant l I: x > 0, y > 0 II: x < 0, y > 0 III: x < 0, y < 0 IV: x > 0, y < 0

Signs of the Trigonometric Functions

Signs of the Trigonometric Functions l Example: Problem: If sin µ < 0 and cos µ > 0, name the quadrant in which the angle µ lies Answer:

Quotient Identities l P = (x, y) corresponding to angle µ: l Get quotient identities:

Quotient Identities l Example. Problem: Given and , find the exact values of the four remaining trigonometric functions of µ using identities. Answer:

Pythagorean Identities l l Unit circle: x 2 + y 2 = 1 (sin µ)2 + (cos µ)2 = 1 sin 2 µ + cos 2 µ = 1 tan 2 µ + 1 = sec 2 µ 1 + cot 2 µ = csc 2 µ

Pythagorean Identities l Example. Find the exact values of each expression. Do not use a calculator (a) Problem: cos 20± sec 20± Answer: (b) Problem: tan 2 25± { sec 2 25± Answer:

Pythagorean Identities l Example. Problem: Given that µ is in Quadrant II, find cos µ. Answer: and that

Even-Odd Properties l l A function f is even if f({µ) = f(µ) for all µ in the domain of f A function f is odd if f({µ) = {f(µ) for all µ in the domain of f
![EvenOdd Properties l Theorem EvenOdd Properties sinµ sinµ cosµ cosµ tanµ Even-Odd Properties l Theorem. [Even-Odd Properties] sin({µ) = {sin(µ) cos({µ) = cos(µ) tan({µ) =](https://slidetodoc.com/presentation_image_h2/70ef81d09aa3c1d06707c9c09ec54632/image-57.jpg)
Even-Odd Properties l Theorem. [Even-Odd Properties] sin({µ) = {sin(µ) cos({µ) = cos(µ) tan({µ) = {tan(µ) csc({µ) = {csc(µ) sec({µ) = sec(µ) cot({µ) = {cot(µ) l l Cosine and secant are even functions The other functions are odd functions

Even-Odd Properties l Example. Find the exact values of (a) Problem: sin({30±) Answer: (b) Problem: Answer: (c) Problem: Answer:

Fundamental Trigonometric Identities l Quotient Identities l Reciprocal Identities l Pythagorean Identities l Even-Odd Identities

Key Points l l l l Domains of Trigonometric Functions Ranges of Trigonometric Functions Periods of Trigonometric Functions Signs of the Trigonometric Functions Quotient Identities Pythagorean Identities Even-Odd Properties Fundamental Trigonometric Identities

Graphs of the Sine and Cosine Functions Section 5. 4

Graphing Trigonometric Functions l l Graph in xy-plane Write functions as l l l l y y y = = = f(x) f(x) = = = sin x cos x tan x csc x sec x cot x Variable x is an angle, measured in radians l Can be any real number

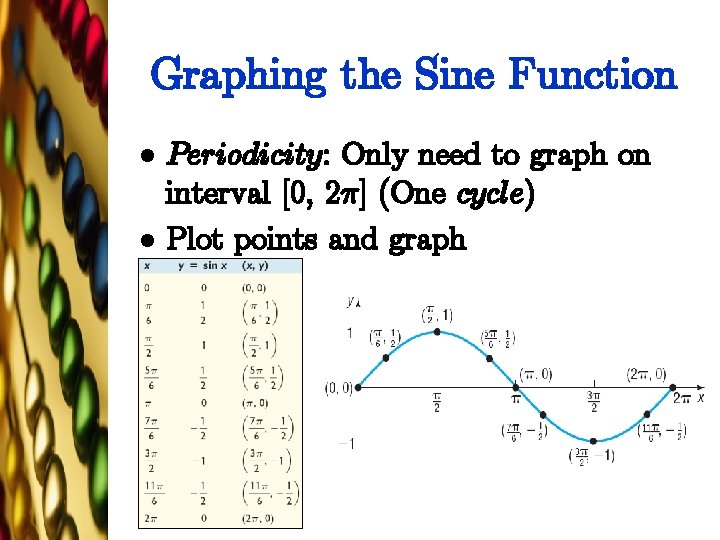
Graphing the Sine Function l l Periodicity: Only need to graph on interval [0, 2¼] (One cycle) Plot points and graph
![Properties of the Sine Function l Domain All real numbers l Range 1 1 Properties of the Sine Function l Domain: All real numbers l Range: [{1, 1]](https://slidetodoc.com/presentation_image_h2/70ef81d09aa3c1d06707c9c09ec54632/image-64.jpg)
Properties of the Sine Function l Domain: All real numbers l Range: [{1, 1] l Odd function l Periodic, period 2¼ l x-intercepts: …, {2¼, {¼, 0, ¼, 2¼, 3¼, … l y-intercept: 0 l Maximum value: y = 1, occurring at l Minimum value: y = {1, occurring at

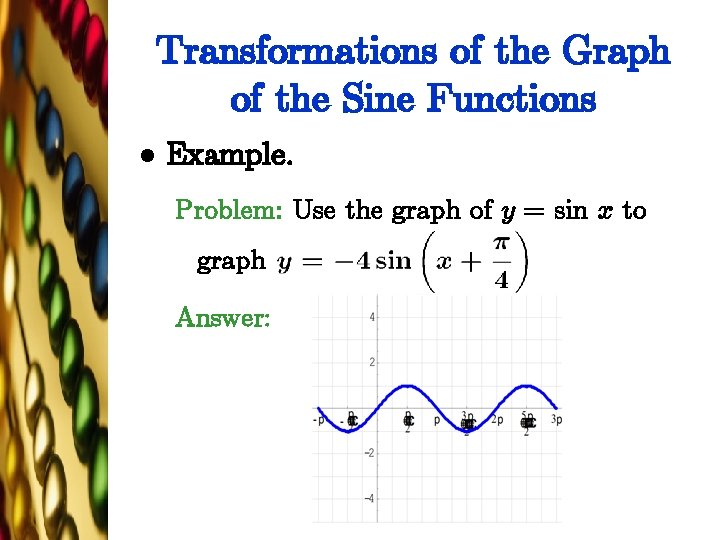
Transformations of the Graph of the Sine Functions l Example. Problem: Use the graph of y = sin x to graph Answer:

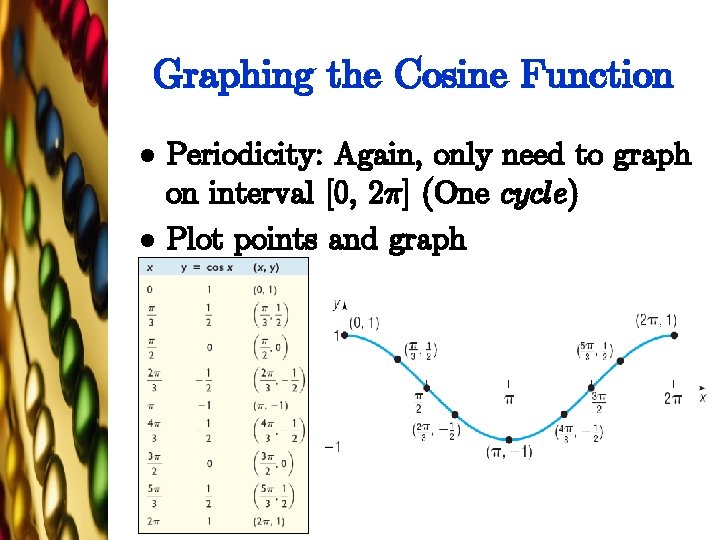
Graphing the Cosine Function l l Periodicity: Again, only need to graph on interval [0, 2¼] (One cycle) Plot points and graph
![Properties of the Cosine Function l Domain All real numbers l Range 1 1 Properties of the Cosine Function l Domain: All real numbers l Range: [{1, 1]](https://slidetodoc.com/presentation_image_h2/70ef81d09aa3c1d06707c9c09ec54632/image-67.jpg)
Properties of the Cosine Function l Domain: All real numbers l Range: [{1, 1] l Even function Periodic, period 2¼ x-intercepts: y-intercept: 1 Maximum value: y = 1, occurring at x = …, {2¼, 0, 2¼, 4¼, 6¼, … Minimum value: y = {1, occurring at x = …, {¼, ¼, 3¼, 5¼, … l l l

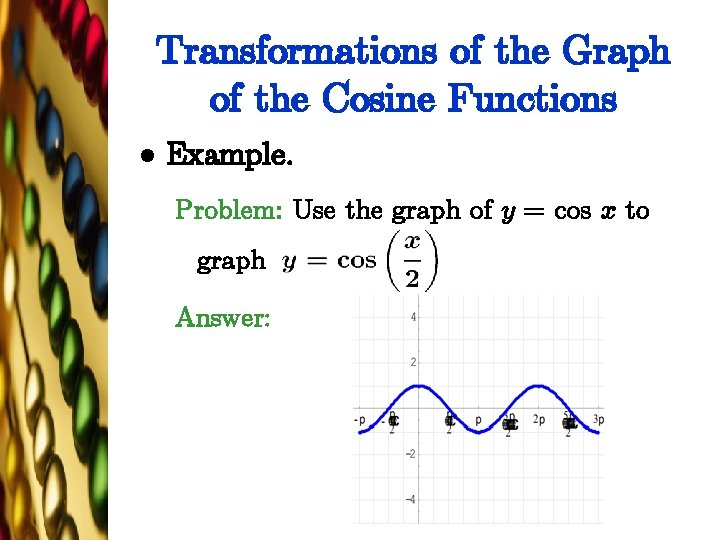
Transformations of the Graph of the Cosine Functions l Example. Problem: Use the graph of y = cos x to graph Answer:

Sinusoidal Graphs l l l Graphs of sine and cosine functions appear to be translations of each other Graphs are called sinusoidal Conjecture.

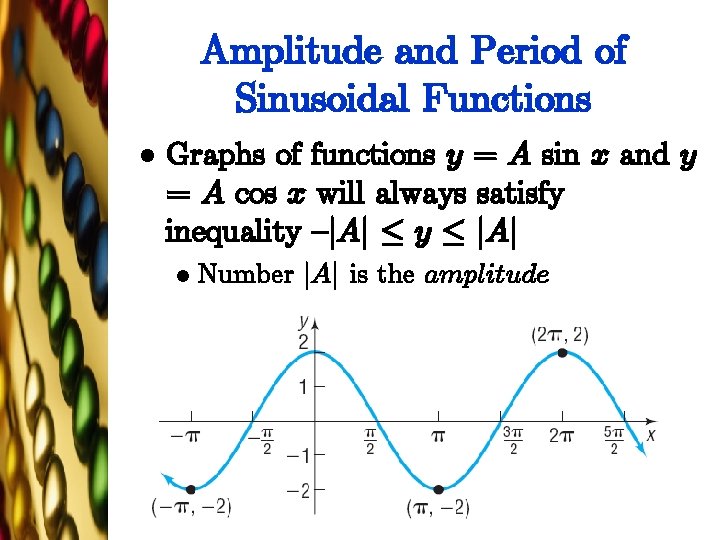
Amplitude and Period of Sinusoidal Functions l Graphs of functions y = A sin x and y = A cos x will always satisfy inequality {j. Aj · y · j. Aj l Number j. Aj is the amplitude

Amplitude and Period of Sinusoidal Functions l Graphs of functions y = A sin x and y = A cos x will always satisfy inequality {j. Aj · y · j. Aj l Number j. Aj is the amplitude

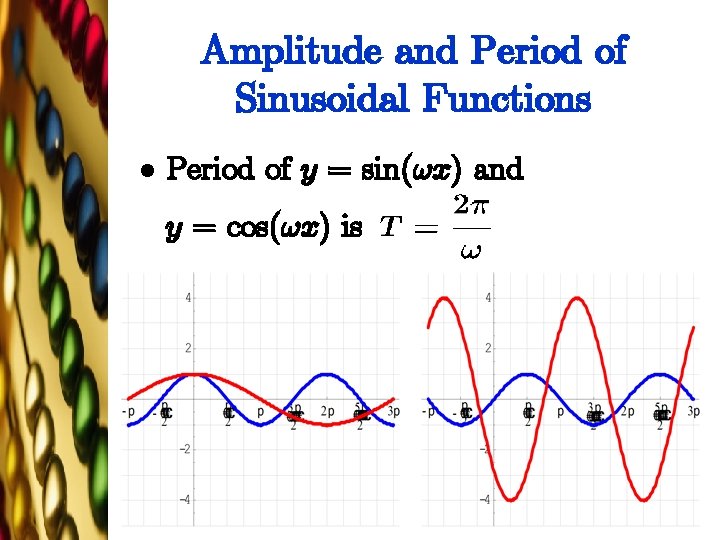
Amplitude and Period of Sinusoidal Functions l Period of y = sin(!x) and y = cos(!x) is

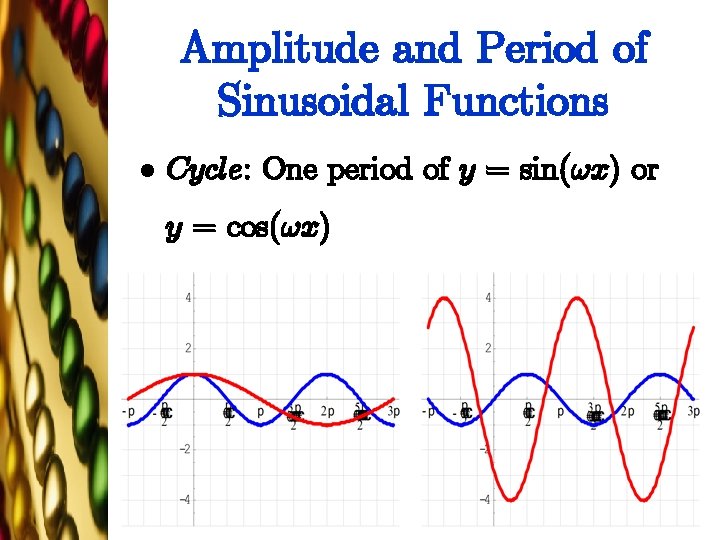
Amplitude and Period of Sinusoidal Functions l Cycle: One period of y = sin(!x) or y = cos(!x)

Amplitude and Period of Sinusoidal Functions l Cycle: One period of y = sin(!x) or y = cos(!x)

Amplitude and Period of Sinusoidal Functions l Theorem. If ! > 0, the amplitude and period of y = Asin(!x) and y = Acos(! x) are given by Amplitude = j Aj Period = .

Amplitude and Period of Sinusoidal Functions l Example. Problem: Determine the amplitude and period of y = {2 cos(¼x) Answer:

Graphing Sinusoidal Functions l One cycle contains four important subintervals For y = sin x and y = cos x these are l Gives five key points on graph l

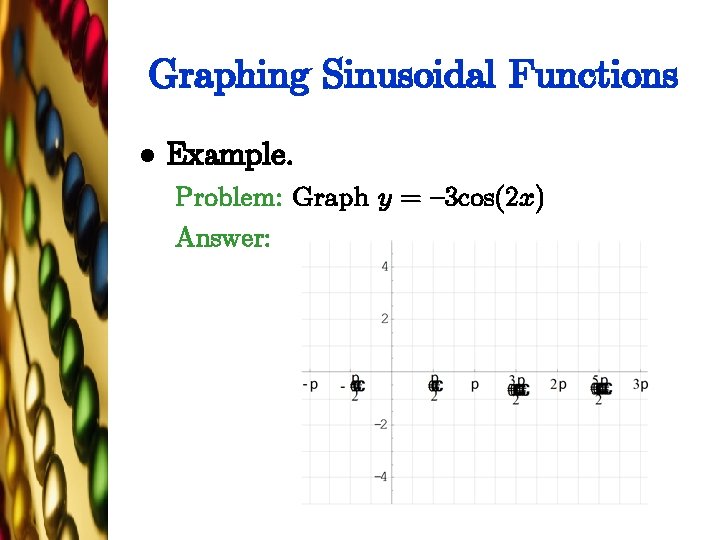
Graphing Sinusoidal Functions l Example. Problem: Graph y = {3 cos(2 x) Answer:

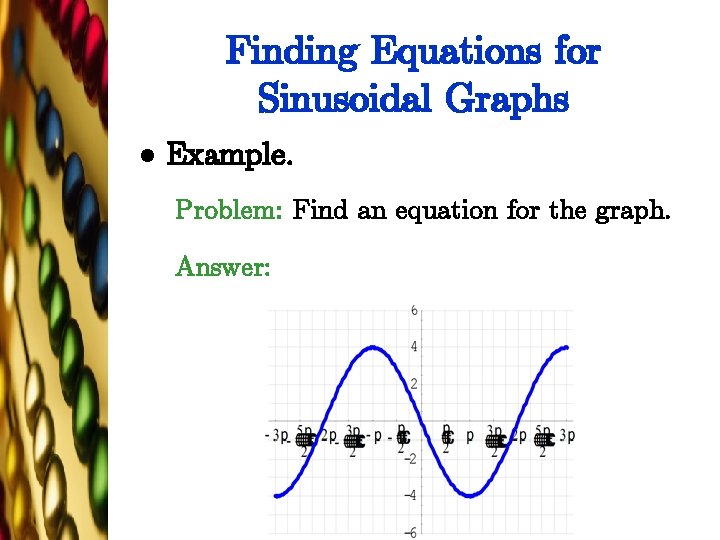
Finding Equations for Sinusoidal Graphs l Example. Problem: Find an equation for the graph. Answer:

Key Points l l l l Graphing Trigonometric Functions Graphing the Sine Function Properties of the Sine Function Transformations of the Graph of the Sine Functions Graphing the Cosine Function Properties of the Cosine Function Transformations of the Graph of the Cosine Functions

Key Points (cont. ) l l Sinusoidal Graphs Amplitude and Period of Sinusoidal Functions Graphing Sinusoidal Functions Finding Equations for Sinusoidal Graphs

Graphs of the Tangent, Cotangent, Cosecant and Secant Functions Section 5. 5

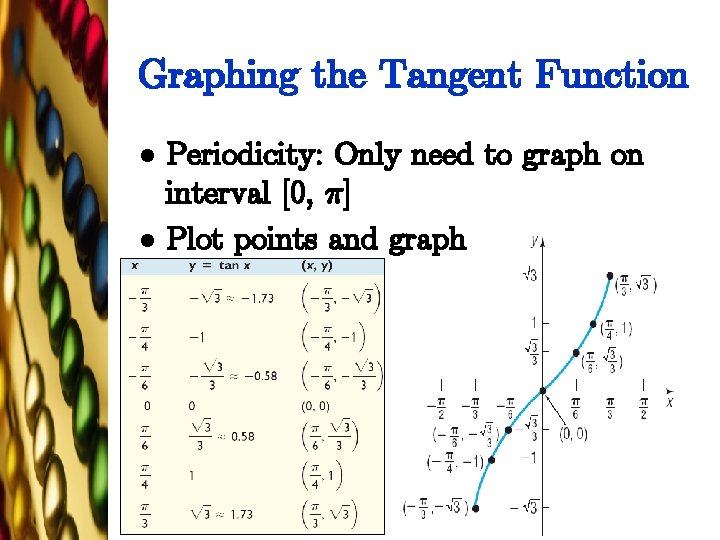
Graphing the Tangent Function l l Periodicity: Only need to graph on interval [0, ¼] Plot points and graph

Properties of the Tangent Function l Domain: All real numbers, except odd multiples of l Range: All real numbers l Odd function l Periodic, period ¼ l x-intercepts: …, {2¼, {¼, 0, ¼, 2¼, 3¼, … l y-intercept: 0 l Asymptotes occur at

Transformations of the Graph of the Tangent Functions l Example. Problem: Use the graph of y = tan x to graph Answer:
![Graphing the Cotangent Function l Periodicity Only need to graph on interval 0 ¼ Graphing the Cotangent Function l Periodicity: Only need to graph on interval [0, ¼]](https://slidetodoc.com/presentation_image_h2/70ef81d09aa3c1d06707c9c09ec54632/image-86.jpg)
Graphing the Cotangent Function l Periodicity: Only need to graph on interval [0, ¼]

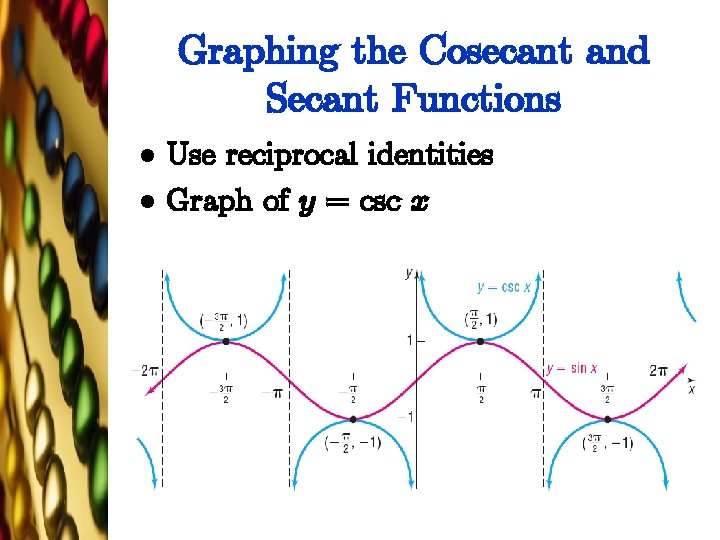
Graphing the Cosecant and Secant Functions l l Use reciprocal identities Graph of y = csc x

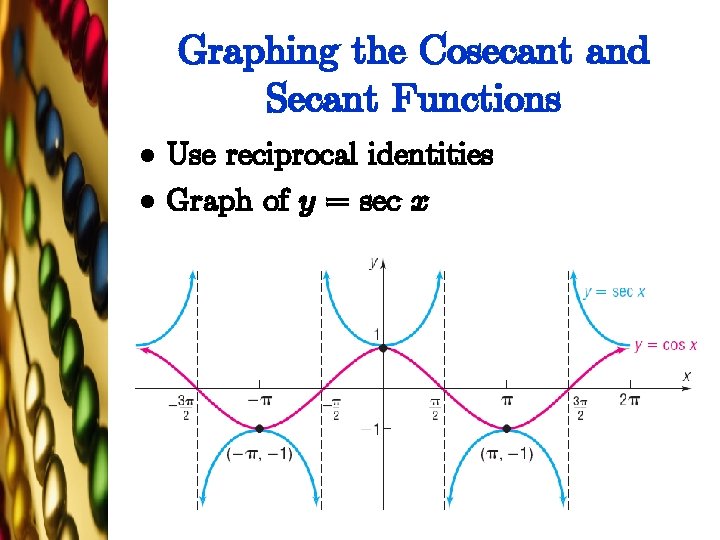
Graphing the Cosecant and Secant Functions l l Use reciprocal identities Graph of y = sec x

Key Points l l l Graphing the Tangent Function Properties of the Tangent Function Transformations of the Graph of the Tangent Functions Graphing the Cotangent Function Graphing the Cosecant and Secant Functions

Phase Shifts; Sinusoidal Curve Fitting Section 5. 6

Graphing Sinusoidal Functions l l y = A sin(!x), ! > 0 l Amplitude j. Aj l Period y = A sin(!x { Á) l Phase shift indicates amount of shift l To right if Á > 0 l To left if Á < 0

Graphing Sinusoidal Functions l Graphing y = A sin(!x { Á) or y = A cos(!x { Á): l Determine amplitude j. Aj l Determine period l Determine starting point of one cycle: l Determine ending point of one cycle:

Graphing Sinusoidal Functions l Graphing y = A sin(!x { Á) or y = A cos(!x { Á): l Divide interval into four subintervals, each with length l Use endpoints of subintervals to find the five key points l Fill in one cycle

Graphing Sinusoidal Functions l Graphing y = A sin(!x { Á) or y = A cos(!x { Á): l Extend the graph in each direction to make it complete

Graphing Sinusoidal Functions l Example. For the equation (a) Problem: Find the amplitude Answer: (b) Problem: Find the period Answer: (c) Problem: Find the phase shift Answer:

Finding a Sinusoidal Function from Data l Example. An experiment in a wind tunnel generates cyclic waves. The following data is collected for 52 seconds. Let v represent the wind speed in feet per second and let x represent the time in seconds. Time (in seconds), x Wind speed (in feet per second), v 0 21 12 42 26 67 41 40 52 20

Finding a Sinusoidal Function from Data l Example. (cont. ) Problem: Write a sine equation that represents the data Answer:

Key Points l l Graphing Sinusoidal Functions Finding a Sinusoidal Function from Data
 Unit circle radians
Unit circle radians ? = 4?²?³/??²
? = 4?²?³/??² Circle j is congruent to circle p
Circle j is congruent to circle p Closed and open circle inequality
Closed and open circle inequality Circle a is tangent to circle b. true false
Circle a is tangent to circle b. true false How to find area of a sector with radians
How to find area of a sector with radians Minor arc length
Minor arc length Area of sector radians
Area of sector radians Lesson 8-2 special right triangles answers
Lesson 8-2 special right triangles answers How to find the reference angle
How to find the reference angle Convert each degree measure into radians
Convert each degree measure into radians Dms to radians
Dms to radians Length of arc calculator
Length of arc calculator S=rθ examples
S=rθ examples Definition of radian
Definition of radian 1/2 radian
1/2 radian Radians quadrants
Radians quadrants 54 degrees to radians
54 degrees to radians Convert from degrees to radians 54
Convert from degrees to radians 54 What is the value of 208º in radians?
What is the value of 208º in radians? Dr frost radians
Dr frost radians Sin22 5 degrees
Sin22 5 degrees Whats a radian
Whats a radian 72 rpm to rad/s
72 rpm to rad/s Tan 585 degrees
Tan 585 degrees Unit 10, unit 10 review tests, unit 10 general test
Unit 10, unit 10 review tests, unit 10 general test Unwrapping the unit circle
Unwrapping the unit circle How to find tan on unit circle
How to find tan on unit circle Unit circle with sin cos tan
Unit circle with sin cos tan Unit circle with tangent labeled
Unit circle with tangent labeled Application of circular functions
Application of circular functions Terminal point on unit circle
Terminal point on unit circle Satc trigonometry
Satc trigonometry How to find the terminal point on the unit circle
How to find the terminal point on the unit circle Satc unit circle
Satc unit circle S act 6 act 3
S act 6 act 3 Coterminal angles unit circle
Coterminal angles unit circle Unit circle memorization tricks
Unit circle memorization tricks Tan 30
Tan 30 Unit circle worksheet c
Unit circle worksheet c 5/13 on unit circle
5/13 on unit circle Unit circle.l
Unit circle.l Coterminal unit circle
Coterminal unit circle Unit circle
Unit circle Pie chart favorite food
Pie chart favorite food Unit circle applet
Unit circle applet 2π/3 συν
2π/3 συν 13 3 the unit circle
13 3 the unit circle 13 3 the unit circle
13 3 the unit circle Unit cirlce
Unit cirlce Trigonometric functions unit circle approach
Trigonometric functions unit circle approach Complex unit circle
Complex unit circle Complex unit circle
Complex unit circle Trigonometric functions unit circle approach
Trigonometric functions unit circle approach Compare and contrast swot, vca, rbv, and 3-circle analysis.
Compare and contrast swot, vca, rbv, and 3-circle analysis. Right triangle trigonometry examples
Right triangle trigonometry examples Unit process and unit operation
Unit process and unit operation Unit operation and unit process
Unit operation and unit process Golden circle human brain
Golden circle human brain Example of sentence with subject and predicate
Example of sentence with subject and predicate Lesson 10-1 circle and circumference
Lesson 10-1 circle and circumference How to calculate circle area with diameter
How to calculate circle area with diameter Find the radius and diameter of each circle
Find the radius and diameter of each circle Label of a circle
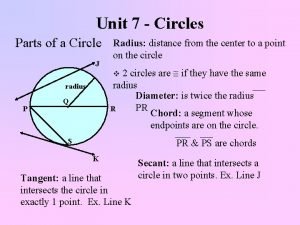
Label of a circle Diameter chord radius tangent secant
Diameter chord radius tangent secant Look and circle the correct option
Look and circle the correct option Circumference of a circle maze
Circumference of a circle maze Area and perimeter of a circle
Area and perimeter of a circle Sector and segment of a circle
Sector and segment of a circle Solute of rubbing alcohol
Solute of rubbing alcohol Red and black flag with yellow circle
Red and black flag with yellow circle A bicycle chain fits tightly
A bicycle chain fits tightly Read the sentences below and
Read the sentences below and Find rs
Find rs Listen and circle a or b
Listen and circle a or b Can a direct object be in a prepositional phrase
Can a direct object be in a prepositional phrase Ellipse drawing in computer graphics
Ellipse drawing in computer graphics Coplanar circle
Coplanar circle Listen read and circle
Listen read and circle Radius and diameter of a circle
Radius and diameter of a circle Chapter 1 matter and change worksheet answers
Chapter 1 matter and change worksheet answers 10-3 areas of circles and sectors
10-3 areas of circles and sectors Label circle
Label circle Direct method of line drawing in computer graphics
Direct method of line drawing in computer graphics The correct answer to complete the sentence is
The correct answer to complete the sentence is Area of a circle
Area of a circle The circle
The circle Circle the subject and
Circle the subject and Cause and effect circle
Cause and effect circle Linking verb examples
Linking verb examples Scan converting ellipse algorithm in computer graphics
Scan converting ellipse algorithm in computer graphics General form of a circle to standard form
General form of a circle to standard form Standard circle
Standard circle Parts of the circle
Parts of the circle Circle in computer graphics
Circle in computer graphics Compass surveying definition
Compass surveying definition Interior and exterior of a circle
Interior and exterior of a circle Suatu lembaga yang
Suatu lembaga yang Si unit to english unit
Si unit to english unit