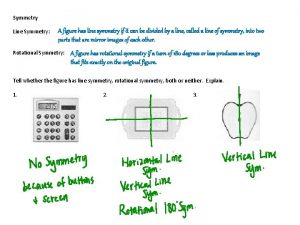
Symmetry Motif the fundamental part of a symmetric








































- Slides: 93



Symmetry Motif: the fundamental part of a symmetric design that, when repeated, creates the whole pattern Operation: some act that reproduces the motif to create the pattern Element: an operation located at a particular point in space

2 -D Symmetry = 360 o/2 rotation to reproduce a motif in a symmetrical pattern A Symmetrical Pattern 6 6 Symmetry Elements 1. Rotation a. Two-fold rotation

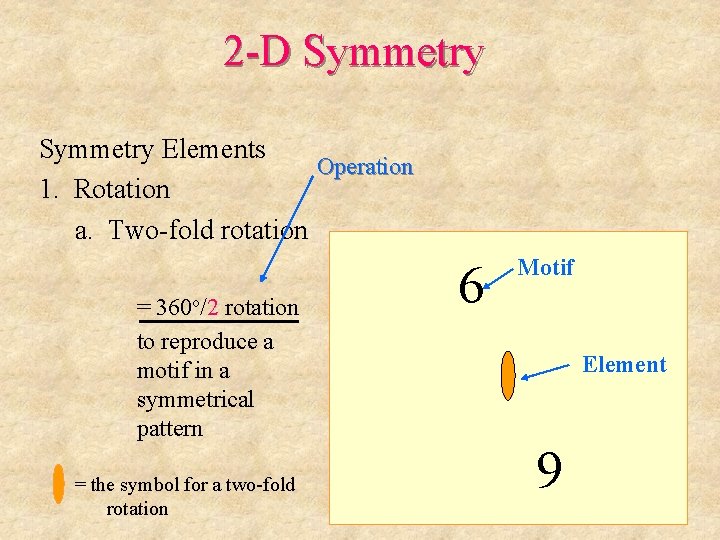
2 -D Symmetry Elements Operation 1. Rotation a. Two-fold rotation = the symbol for a two-fold rotation 6 Element 6 = 360 o/2 rotation to reproduce a motif in a symmetrical pattern Motif

2 -D Symmetry Elements 1. Rotation a. Two-fold rotation = the symbol for a two-fold rotation 6 second operation step 6 = 360 o/2 rotation to reproduce a motif in a symmetrical pattern first operation step

2 -D Symmetry Elements 1. Rotation a. Two-fold rotation Some familiar objects have an intrinsic symmetry

2 -D Symmetry Elements 1. Rotation a. Two-fold rotation Some familiar objects have an intrinsic symmetry

2 -D Symmetry Elements 1. Rotation a. Two-fold rotation Some familiar objects have an intrinsic symmetry

2 -D Symmetry Elements 1. Rotation a. Two-fold rotation Some familiar objects have an intrinsic symmetry

2 -D Symmetry Elements 1. Rotation a. Two-fold rotation Some familiar objects have an intrinsic symmetry

2 -D Symmetry Elements 1. Rotation a. Two-fold rotation Some familiar objects have an intrinsic symmetry

2 -D Symmetry Elements 1. Rotation a. Two-fold rotation Some familiar objects have an intrinsic symmetry 180 o rotation makes it coincident Second 180 o brings the object back to its original position What’s the motif here? ?

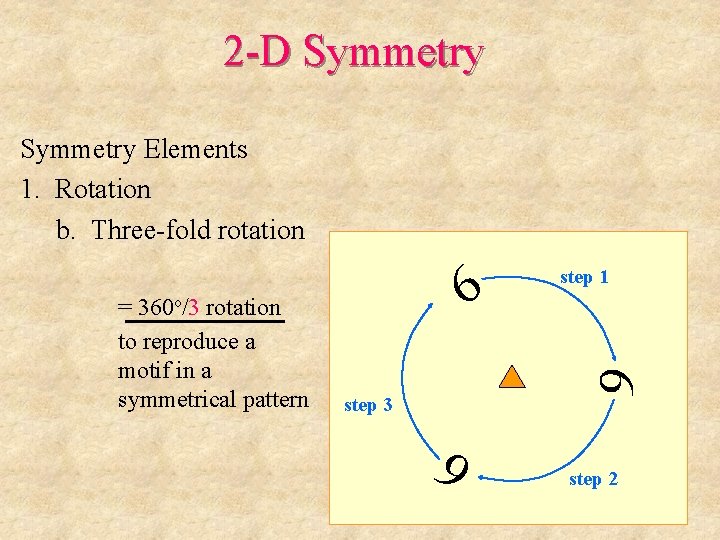
2 -D Symmetry Elements 1. Rotation b. Three-fold rotation 6 6 6 = 360 o/3 rotation to reproduce a motif in a symmetrical pattern

2 -D Symmetry Elements 1. Rotation b. Three-fold rotation 6 6 step 3 6 = 360 o/3 rotation to reproduce a motif in a symmetrical pattern step 1 step 2

2 -D Symmetry Elements 1. Rotation 6 6 6 a identity Z t 9 6 6 Objects with symmetry: 4 -fold 6 3 -fold 6 2 -fold 6 6 6 1 -fold 6 6 -fold d 5 -fold and > 6 -fold rotations will not work in combination with translations in crystals (as we shall see later). Thus we will exclude them now.

4 -fold, 2 -fold, and 3 -fold rotations in a cube Click on image to run animation

2 -D Symmetry Elements 2. Inversion (i) inversion is identical to 2 -fold rotation in 2 -D, but is unique in 3 -D (try it with your hands) 6 6 inversion through a center to reproduce a motif in a symmetrical pattern = symbol for an inversion center

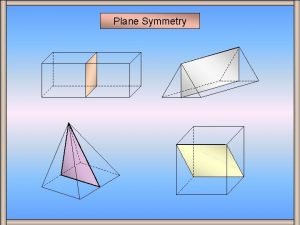
2 -D Symmetry Elements 3. Reflection (m) Reflection across a “mirror plane” reproduces a motif = symbol for a mirror plane

2 -D Symmetry We now have 6 unique 2 -D symmetry operations: 1 2 3 4 6 m Rotations are congruent operations reproductions are identical Inversion and reflection are enantiomorphic operations reproductions are “opposite-handed”

2 -D Symmetry Combinations of symmetry elements are also possible To create a complete analysis of symmetry about a point in space, we must try all possible combinations of these symmetry elements In the interest of clarity and ease of illustration, we continue to consider only 2 -D examples

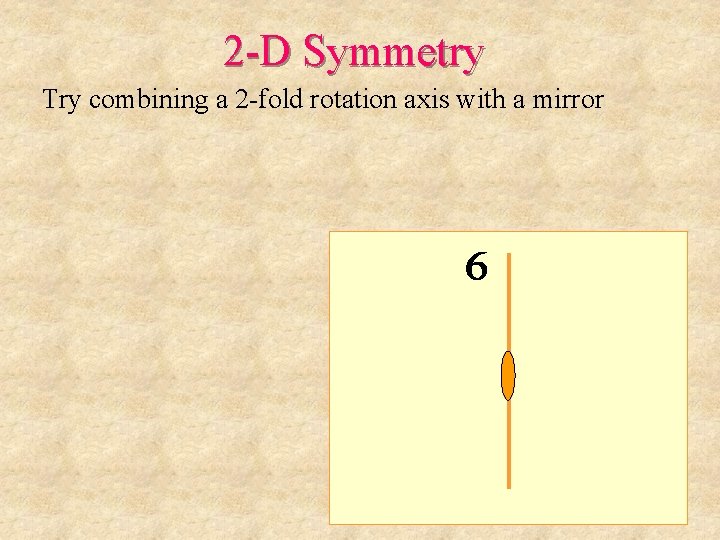
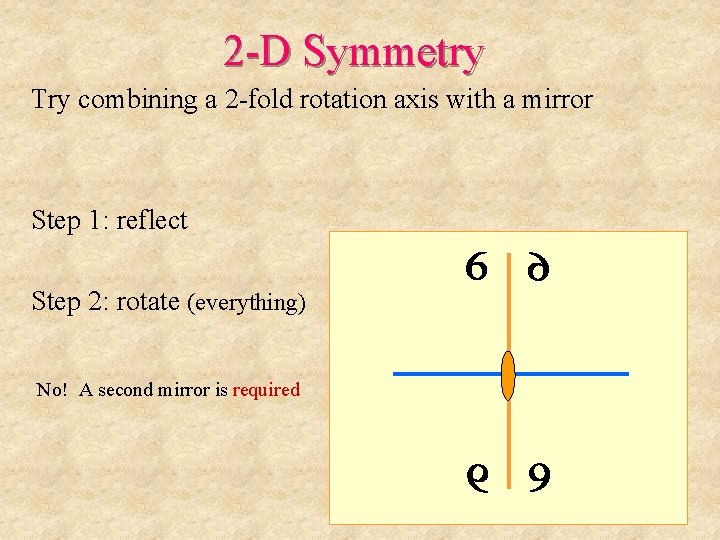
2 -D Symmetry Try combining a 2 -fold rotation axis with a mirror

2 -D Symmetry Try combining a 2 -fold rotation axis with a mirror Step 1: reflect (could do either step first)

2 -D Symmetry Try combining a 2 -fold rotation axis with a mirror Step 1: reflect Step 2: rotate (everything)

2 -D Symmetry Try combining a 2 -fold rotation axis with a mirror Step 1: reflect Step 2: rotate (everything) Is that all? ?

2 -D Symmetry Try combining a 2 -fold rotation axis with a mirror Step 1: reflect Step 2: rotate (everything) No! A second mirror is required

2 -D Symmetry Try combining a 2 -fold rotation axis with a mirror The result is Point Group 2 mm “ 2 mm” indicates 2 mirrors The mirrors are different (not equivalent by symmetry)

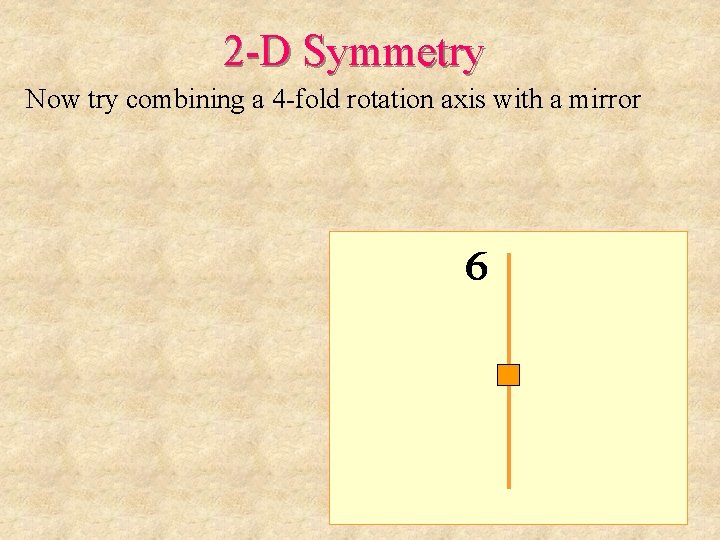
2 -D Symmetry Now try combining a 4 -fold rotation axis with a mirror

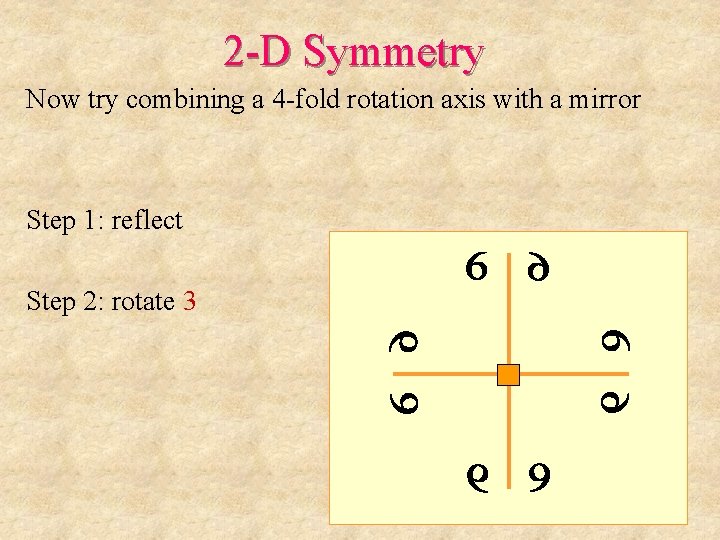
2 -D Symmetry Now try combining a 4 -fold rotation axis with a mirror Step 1: reflect

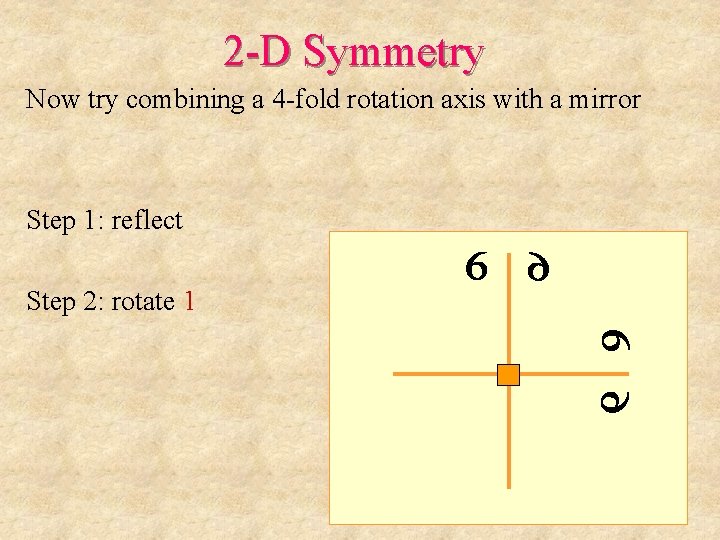
2 -D Symmetry Now try combining a 4 -fold rotation axis with a mirror Step 1: reflect Step 2: rotate 1

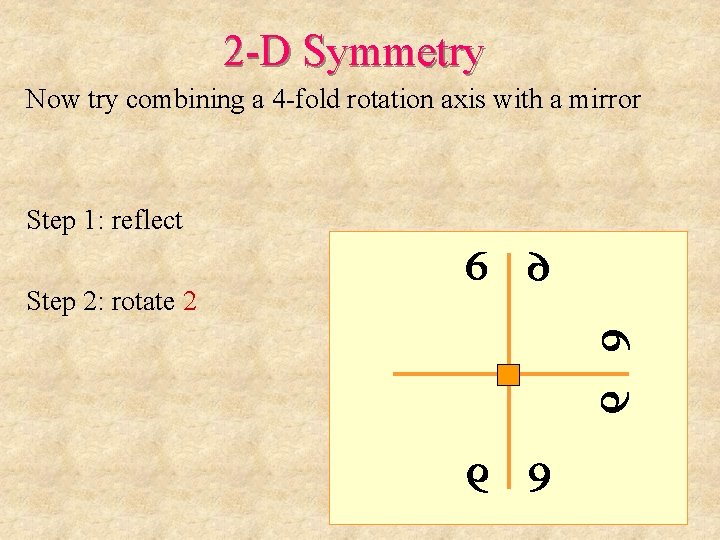
2 -D Symmetry Now try combining a 4 -fold rotation axis with a mirror Step 1: reflect Step 2: rotate 2

2 -D Symmetry Now try combining a 4 -fold rotation axis with a mirror Step 1: reflect Step 2: rotate 3

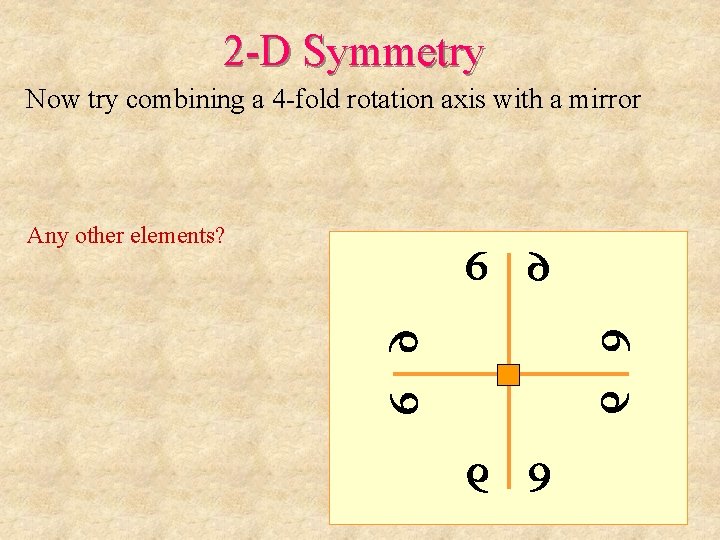
2 -D Symmetry Now try combining a 4 -fold rotation axis with a mirror Any other elements?

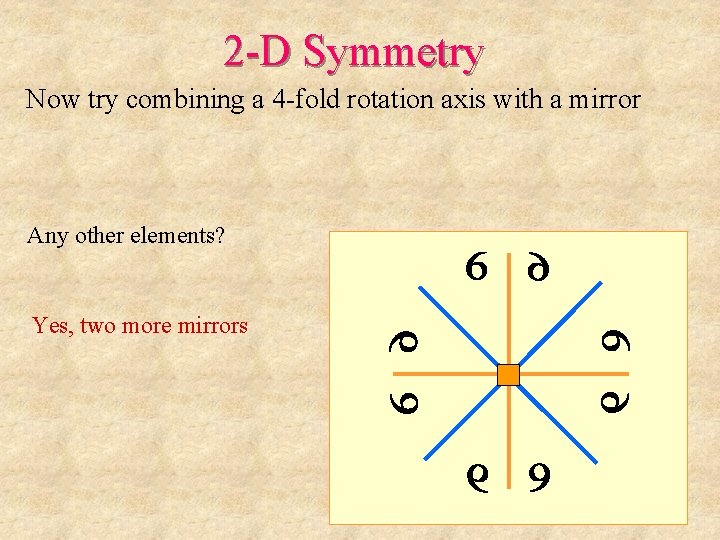
2 -D Symmetry Now try combining a 4 -fold rotation axis with a mirror Any other elements? Yes, two more mirrors

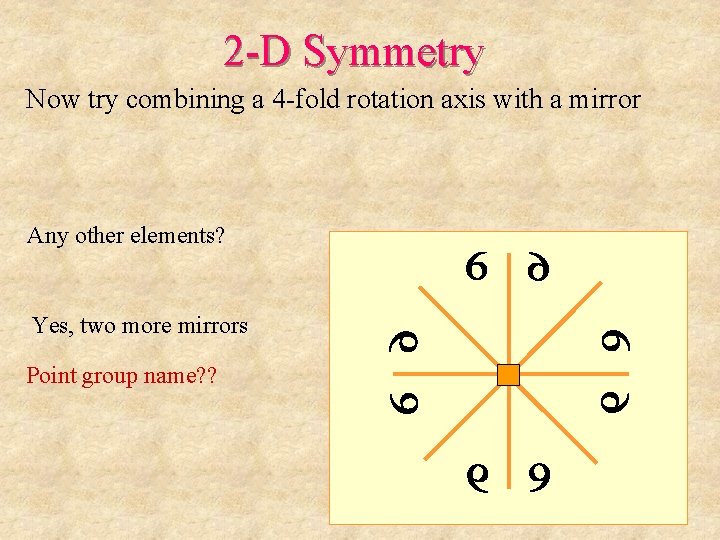
2 -D Symmetry Now try combining a 4 -fold rotation axis with a mirror Any other elements? Yes, two more mirrors Point group name? ?

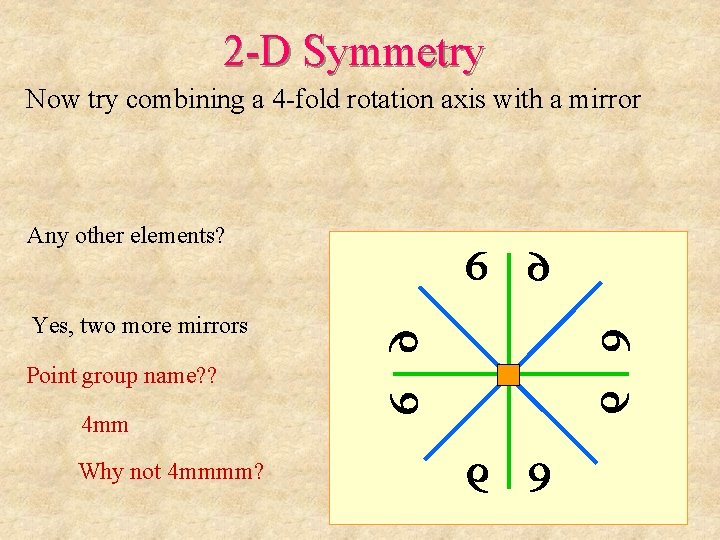
2 -D Symmetry Now try combining a 4 -fold rotation axis with a mirror Any other elements? Yes, two more mirrors Point group name? ? 4 mm Why not 4 mmmm?

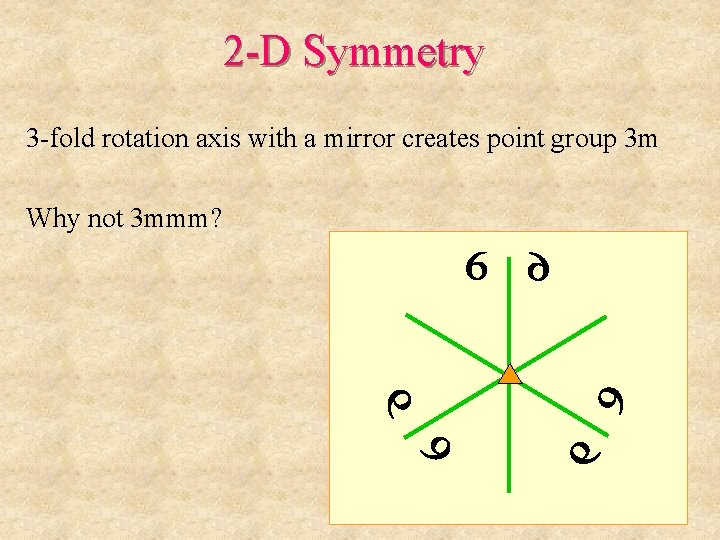
2 -D Symmetry 3 -fold rotation axis with a mirror creates point group 3 m Why not 3 mmm?

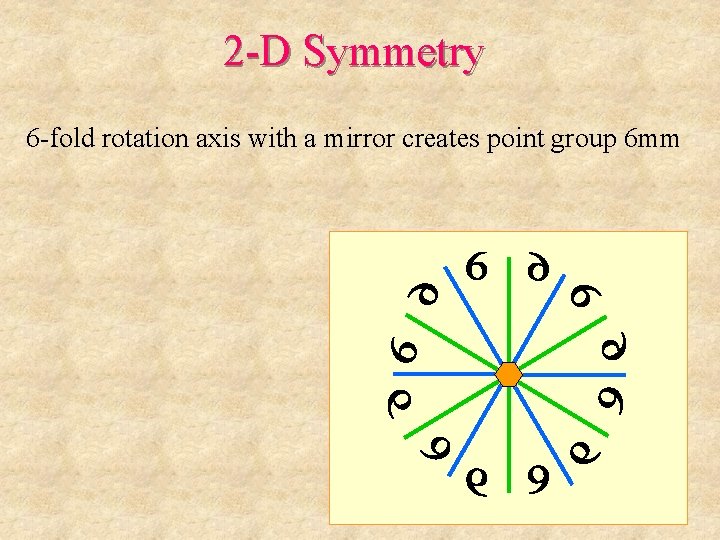
2 -D Symmetry 6 -fold rotation axis with a mirror creates point group 6 mm

2 -D Symmetry All other combinations are either: Incompatible (2 + 2 cannot be done in 2 -D) Redundant with others already tried m + m 2 mm because creates 2 -fold This is the same as 2 + m 2 mm

2 -D Symmetry The original 6 elements plus the 4 combinations creates 10 possible 2 -D Point Groups: 1 2 3 4 6 m 2 mm 3 m 4 mm 6 mm Any 2 -D pattern of objects surrounding a point must conform to one of these groups

3 -D Symmetry New 3 -D Symmetry Elements 4. Rotoinversion a. 1 -fold rotoinversion ( 1 )

3 -D Symmetry New 3 -D Symmetry Elements 4. Rotoinversion a. 1 -fold rotoinversion ( 1 ) Step 1: rotate 360/1 (identity)

3 -D Symmetry New 3 -D Symmetry Elements 4. Rotoinversion a. 1 -fold rotoinversion ( 1 ) Step 1: rotate 360/1 (identity) Step 2: invert This is the same as i, so not a new operation

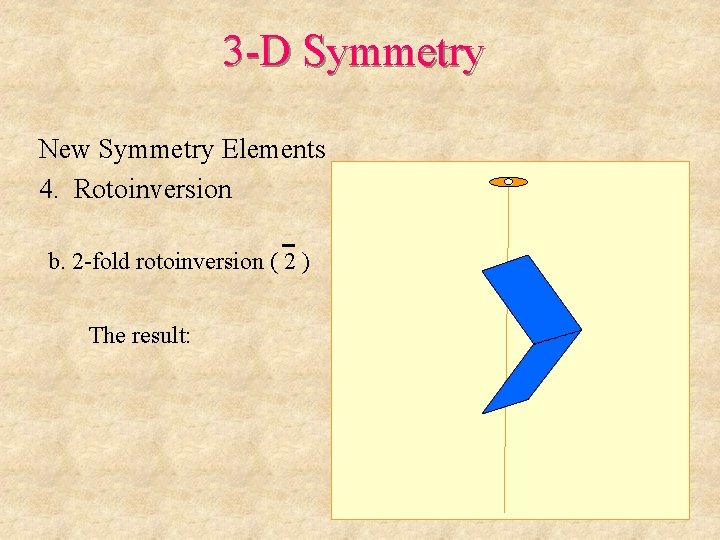
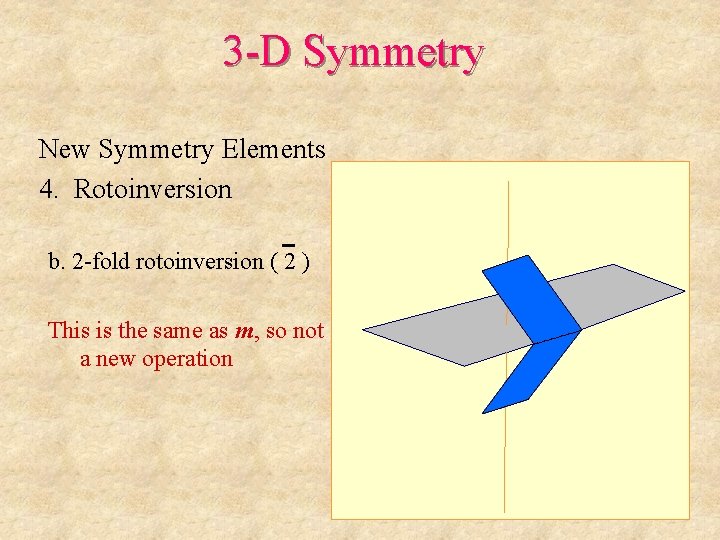
3 -D Symmetry New Symmetry Elements 4. Rotoinversion b. 2 -fold rotoinversion ( 2 ) Step 1: rotate 360/2 Note: this is a temporary step, the intermediate motif element does not exist in the final pattern

3 -D Symmetry New Symmetry Elements 4. Rotoinversion b. 2 -fold rotoinversion ( 2 ) Step 1: rotate 360/2 Step 2: invert

3 -D Symmetry New Symmetry Elements 4. Rotoinversion b. 2 -fold rotoinversion ( 2 ) The result:

3 -D Symmetry New Symmetry Elements 4. Rotoinversion b. 2 -fold rotoinversion ( 2 ) This is the same as m, so not a new operation

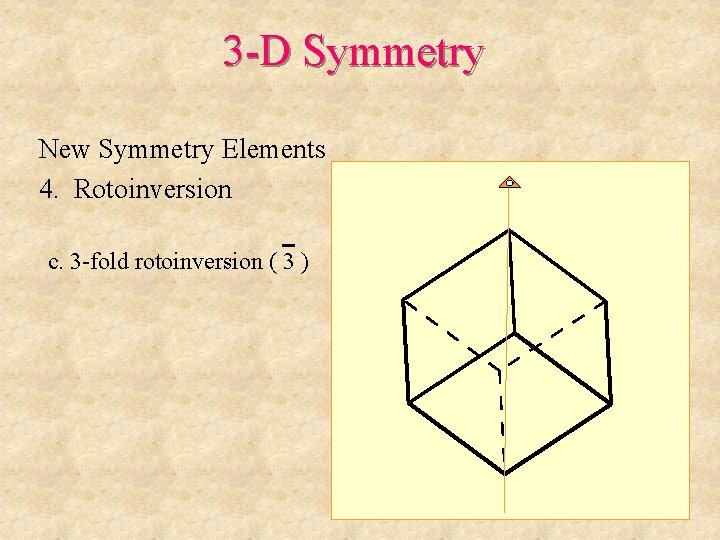
3 -D Symmetry New Symmetry Elements 4. Rotoinversion c. 3 -fold rotoinversion ( 3 )

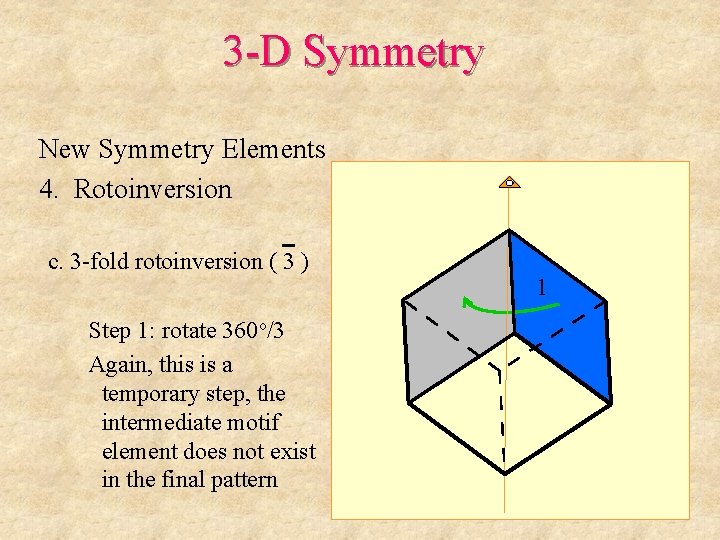
3 -D Symmetry New Symmetry Elements 4. Rotoinversion c. 3 -fold rotoinversion ( 3 ) Step 1: rotate 360 o/3 Again, this is a temporary step, the intermediate motif element does not exist in the final pattern 1

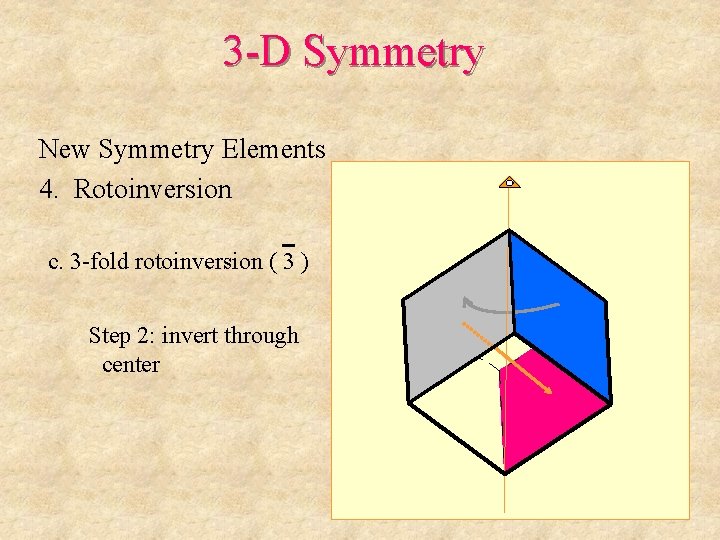
3 -D Symmetry New Symmetry Elements 4. Rotoinversion c. 3 -fold rotoinversion ( 3 ) Step 2: invert through center

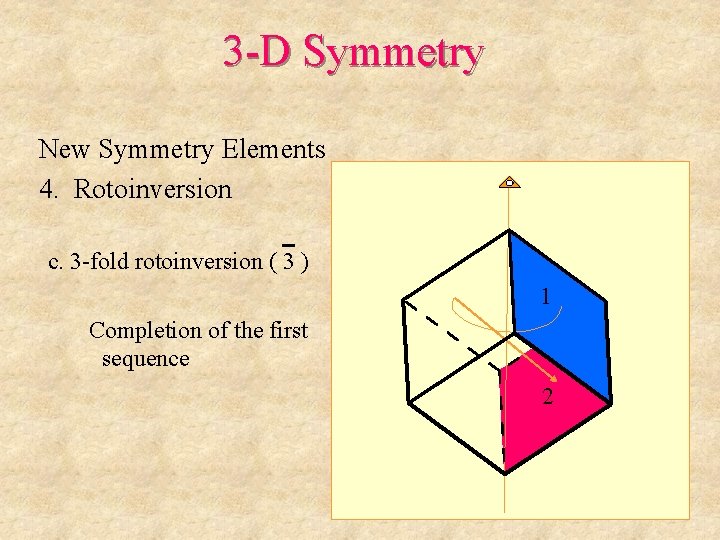
3 -D Symmetry New Symmetry Elements 4. Rotoinversion c. 3 -fold rotoinversion ( 3 ) 1 Completion of the first sequence 2

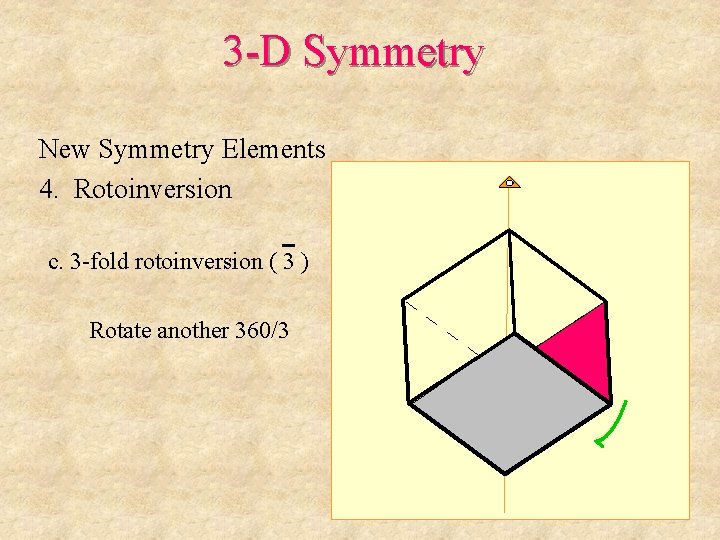
3 -D Symmetry New Symmetry Elements 4. Rotoinversion c. 3 -fold rotoinversion ( 3 ) Rotate another 360/3

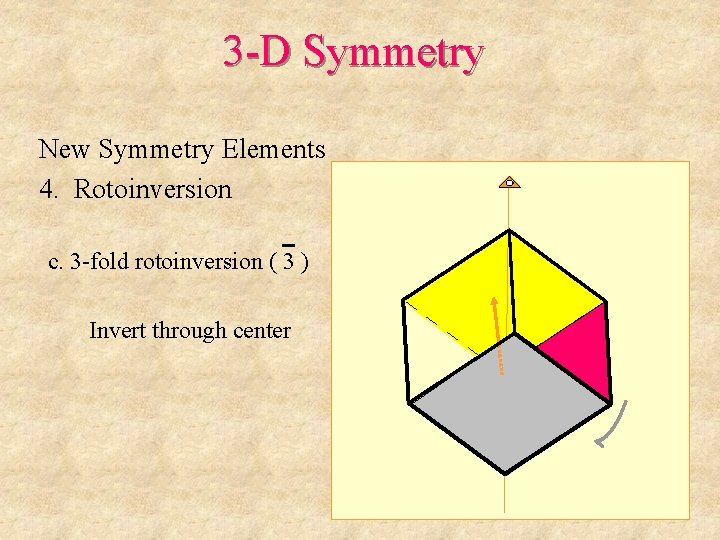
3 -D Symmetry New Symmetry Elements 4. Rotoinversion c. 3 -fold rotoinversion ( 3 ) Invert through center

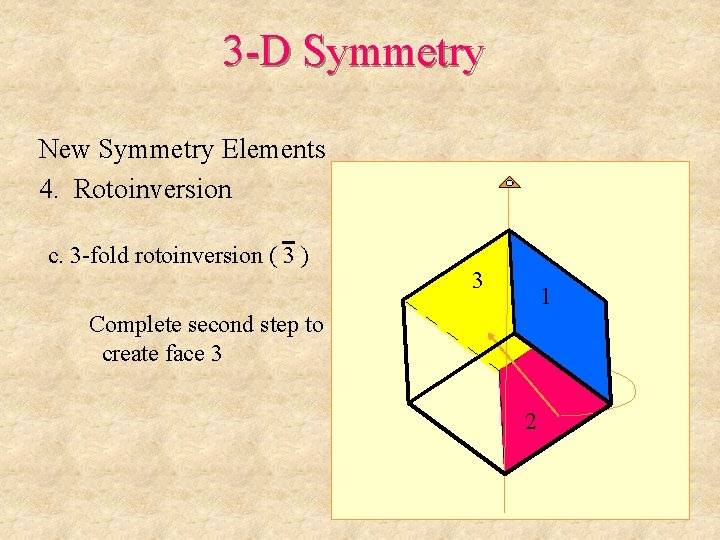
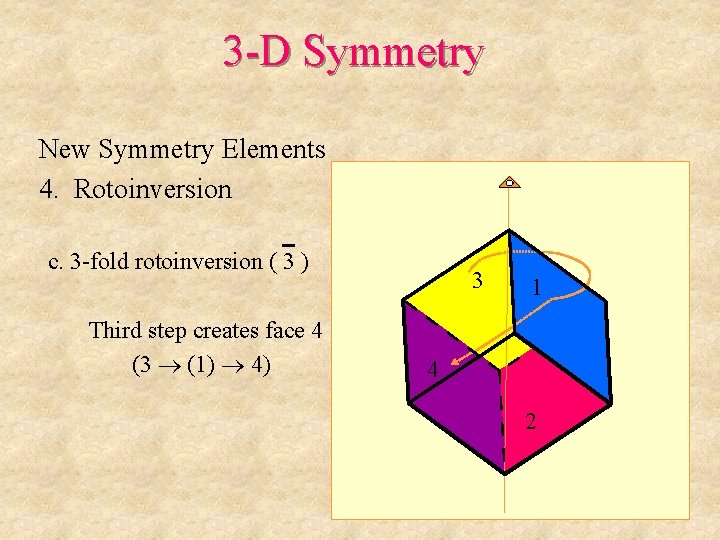
3 -D Symmetry New Symmetry Elements 4. Rotoinversion c. 3 -fold rotoinversion ( 3 ) 3 1 Complete second step to create face 3 2

3 -D Symmetry New Symmetry Elements 4. Rotoinversion c. 3 -fold rotoinversion ( 3 ) Third step creates face 4 (3 (1) 4) 3 1 4 2

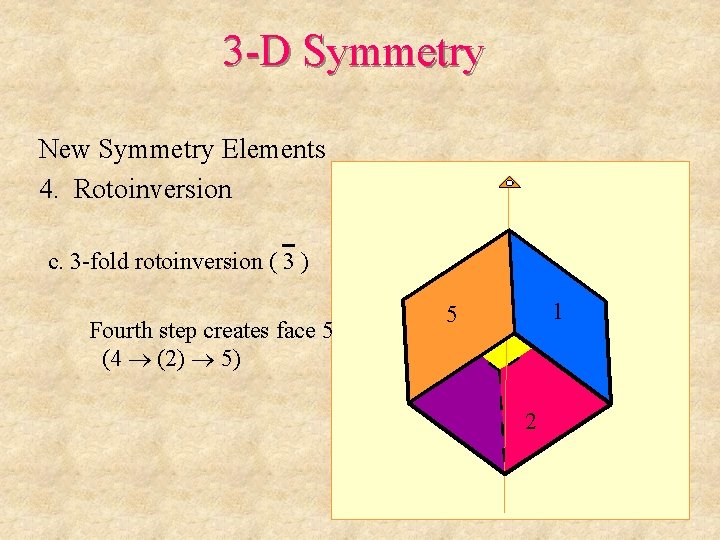
3 -D Symmetry New Symmetry Elements 4. Rotoinversion c. 3 -fold rotoinversion ( 3 ) Fourth step creates face 5 (4 (2) 5) 1 5 2

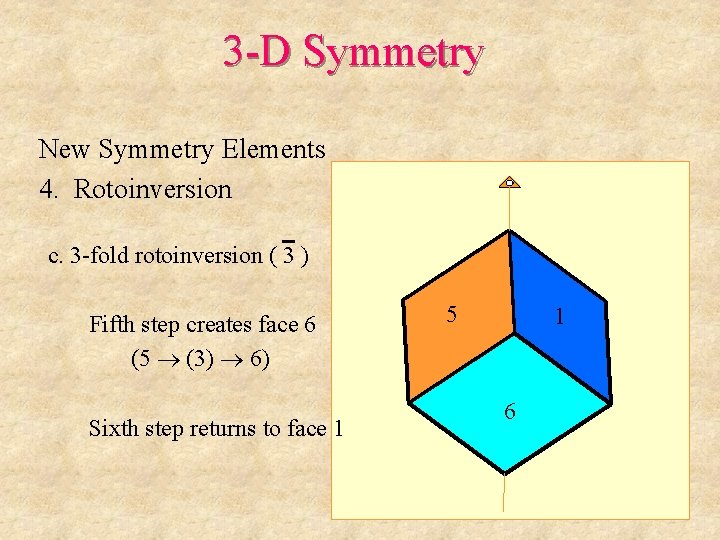
3 -D Symmetry New Symmetry Elements 4. Rotoinversion c. 3 -fold rotoinversion ( 3 ) Fifth step creates face 6 (5 (3) 6) Sixth step returns to face 1 5 1 6

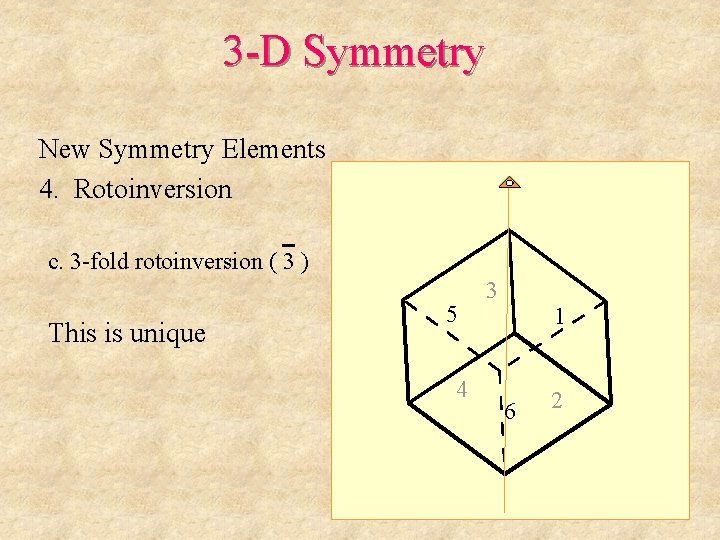
3 -D Symmetry New Symmetry Elements 4. Rotoinversion c. 3 -fold rotoinversion ( 3 ) This is unique 5 4 3 1 6 2

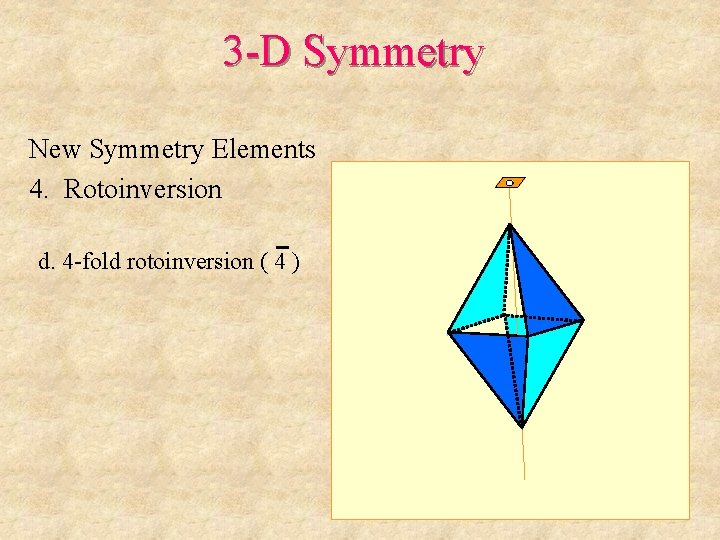
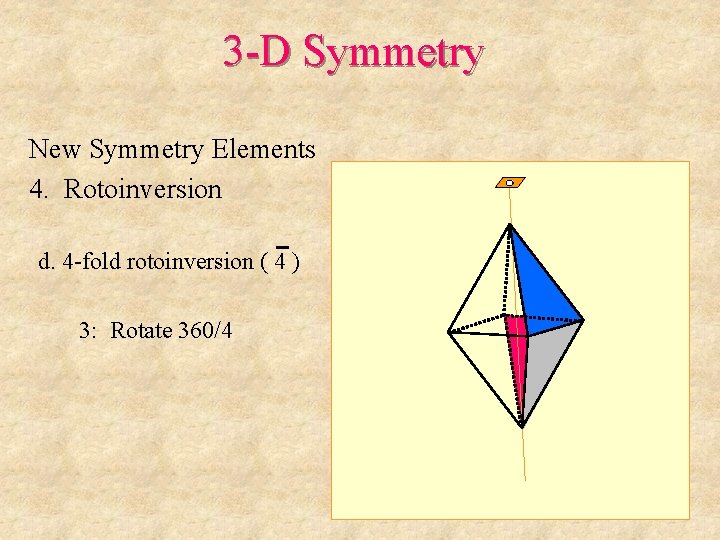
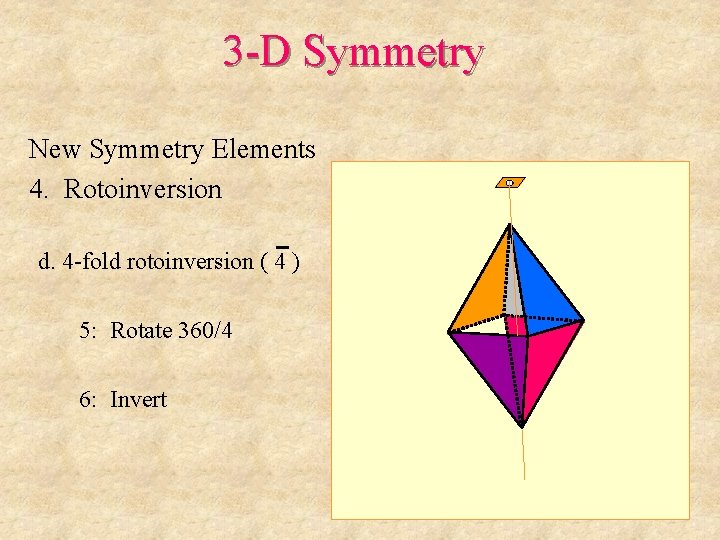
3 -D Symmetry New Symmetry Elements 4. Rotoinversion d. 4 -fold rotoinversion ( 4 )

3 -D Symmetry New Symmetry Elements 4. Rotoinversion d. 4 -fold rotoinversion ( 4 )

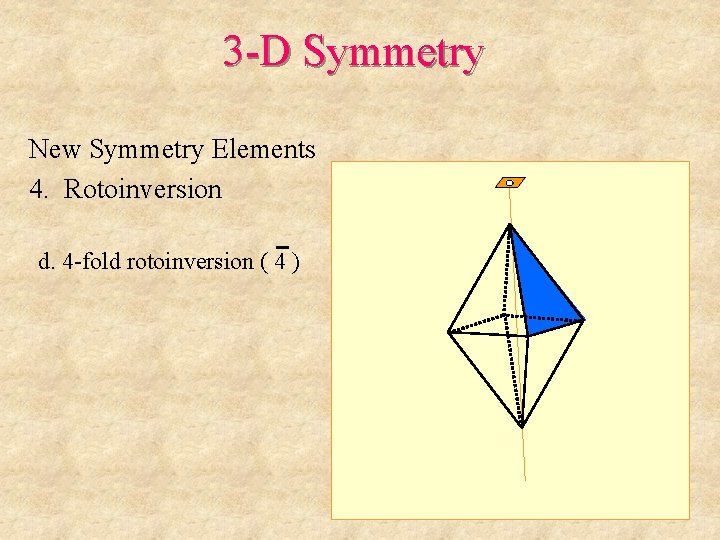
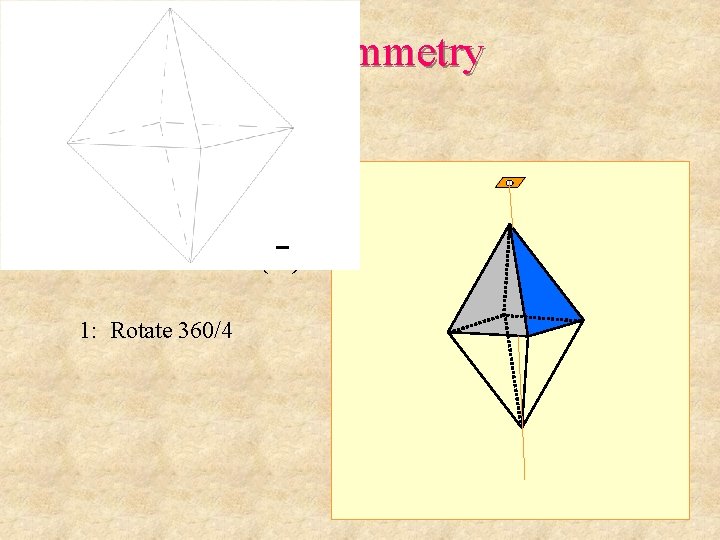
3 -D Symmetry New Symmetry Elements 4. Rotoinversion d. 4 -fold rotoinversion ( 4 ) 1: Rotate 360/4

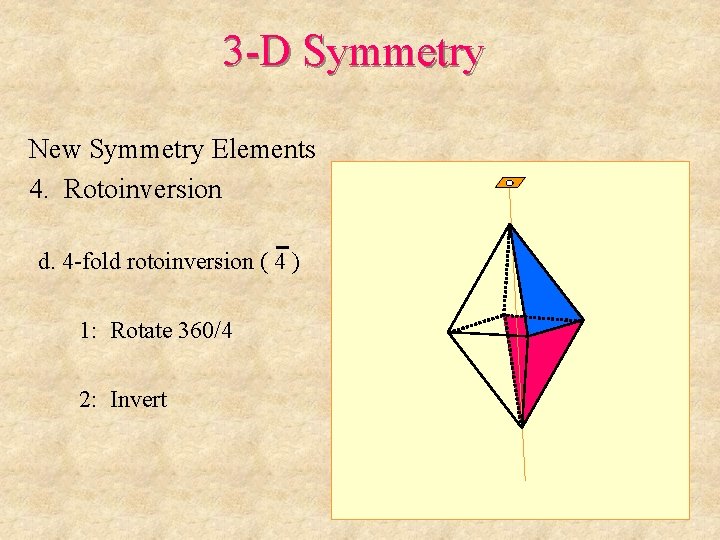
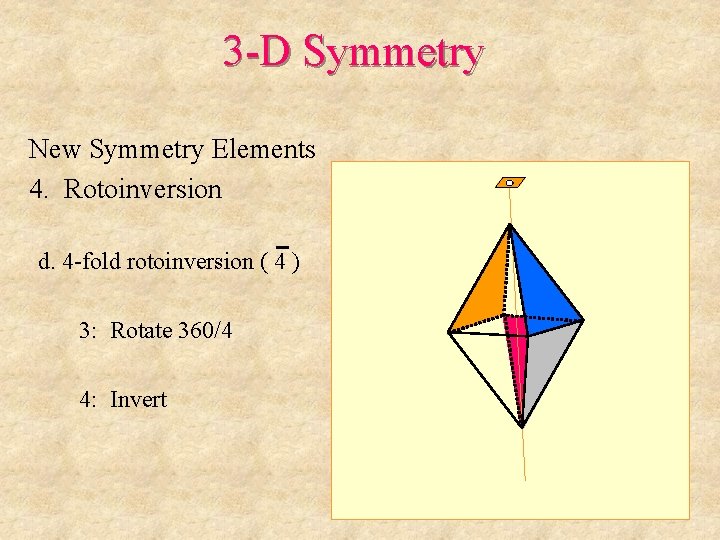
3 -D Symmetry New Symmetry Elements 4. Rotoinversion d. 4 -fold rotoinversion ( 4 ) 1: Rotate 360/4 2: Invert

3 -D Symmetry New Symmetry Elements 4. Rotoinversion d. 4 -fold rotoinversion ( 4 ) 1: Rotate 360/4 2: Invert

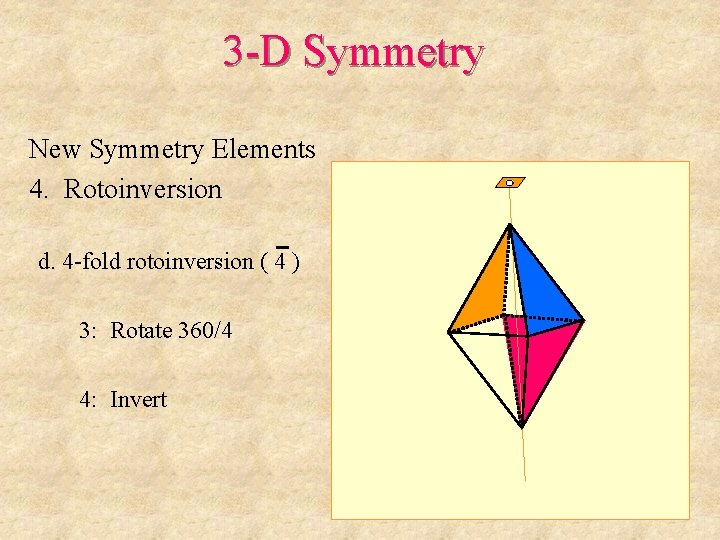
3 -D Symmetry New Symmetry Elements 4. Rotoinversion d. 4 -fold rotoinversion ( 4 ) 3: Rotate 360/4

3 -D Symmetry New Symmetry Elements 4. Rotoinversion d. 4 -fold rotoinversion ( 4 ) 3: Rotate 360/4 4: Invert

3 -D Symmetry New Symmetry Elements 4. Rotoinversion d. 4 -fold rotoinversion ( 4 ) 3: Rotate 360/4 4: Invert

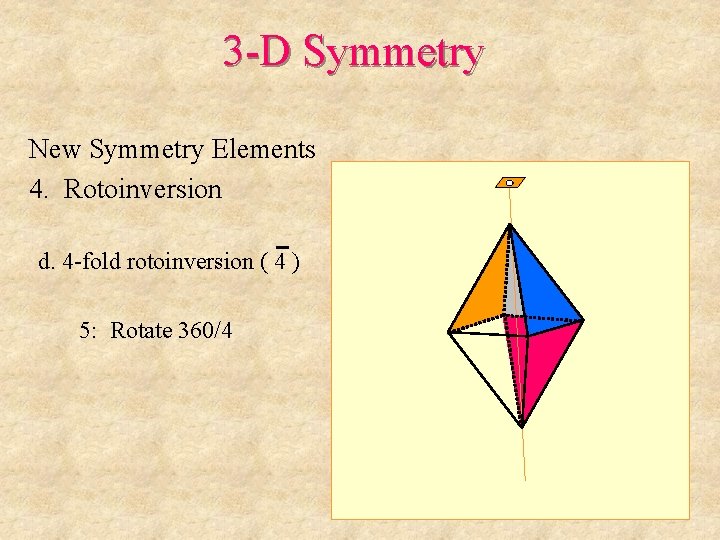
3 -D Symmetry New Symmetry Elements 4. Rotoinversion d. 4 -fold rotoinversion ( 4 ) 5: Rotate 360/4

3 -D Symmetry New Symmetry Elements 4. Rotoinversion d. 4 -fold rotoinversion ( 4 ) 5: Rotate 360/4 6: Invert

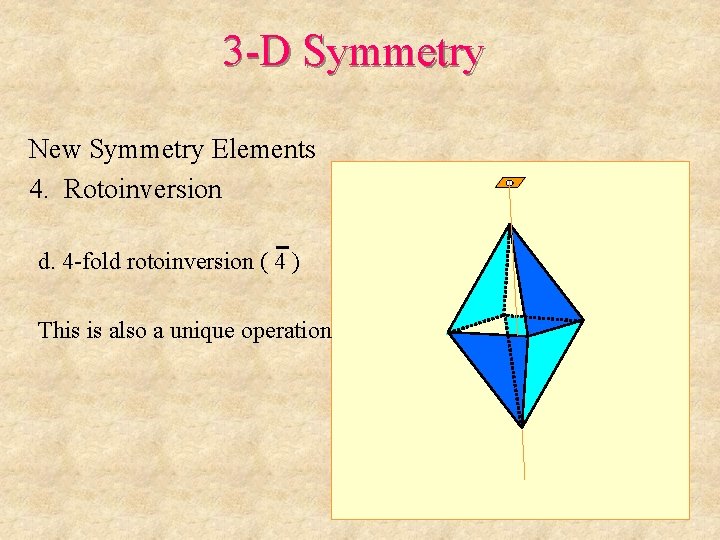
3 -D Symmetry New Symmetry Elements 4. Rotoinversion d. 4 -fold rotoinversion ( 4 ) This is also a unique operation

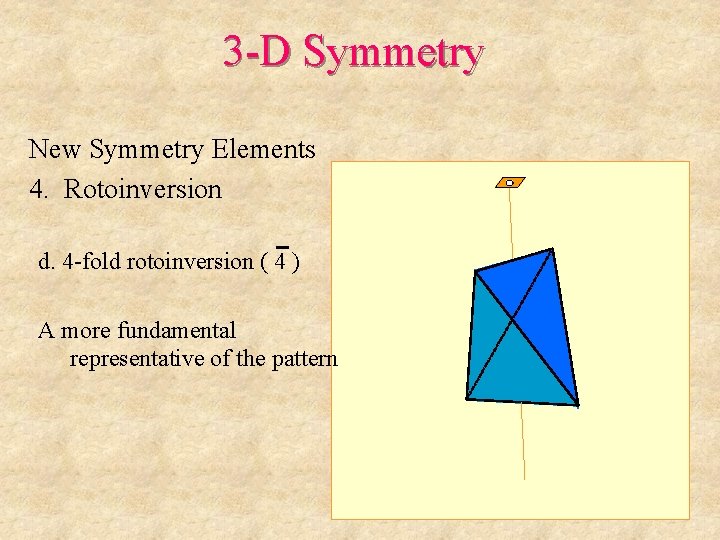
3 -D Symmetry New Symmetry Elements 4. Rotoinversion d. 4 -fold rotoinversion ( 4 ) A more fundamental representative of the pattern

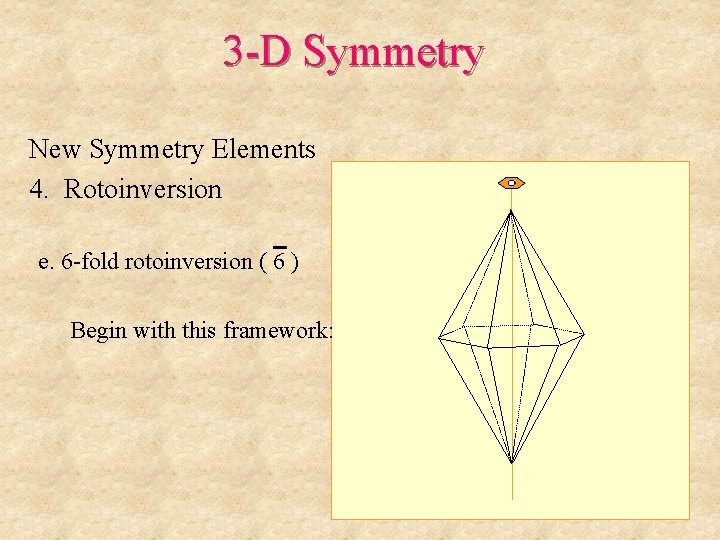
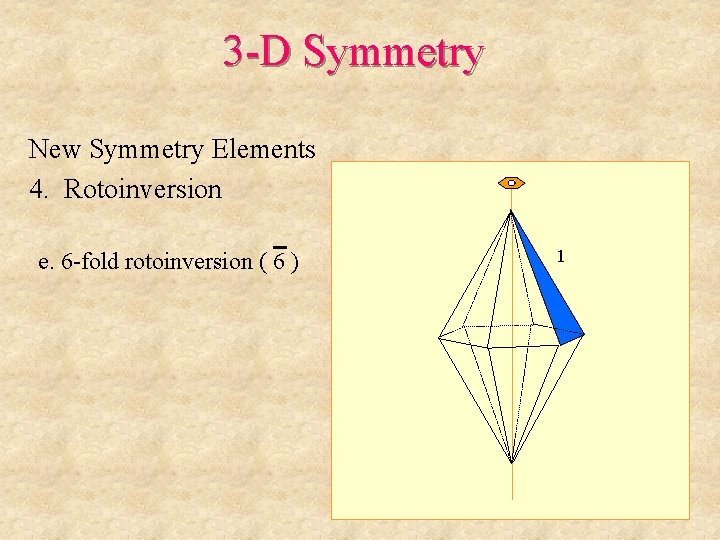
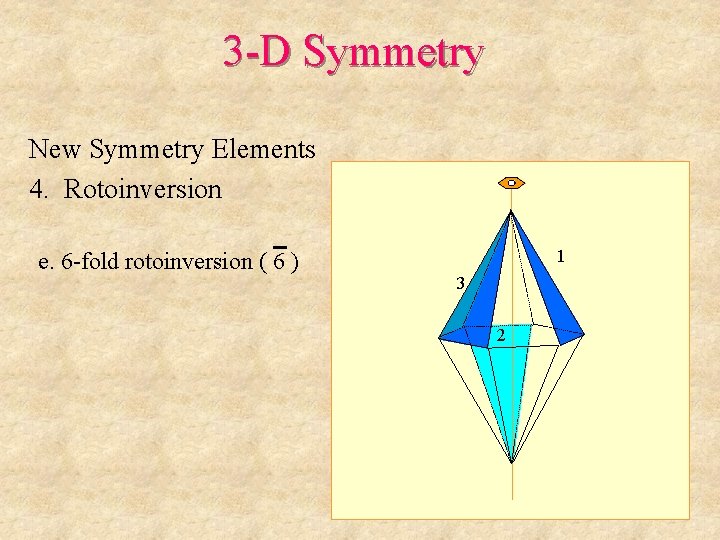
3 -D Symmetry New Symmetry Elements 4. Rotoinversion e. 6 -fold rotoinversion ( 6 ) Begin with this framework:

3 -D Symmetry New Symmetry Elements 4. Rotoinversion e. 6 -fold rotoinversion ( 6 ) 1

3 -D Symmetry New Symmetry Elements 4. Rotoinversion e. 6 -fold rotoinversion ( 6 ) 1

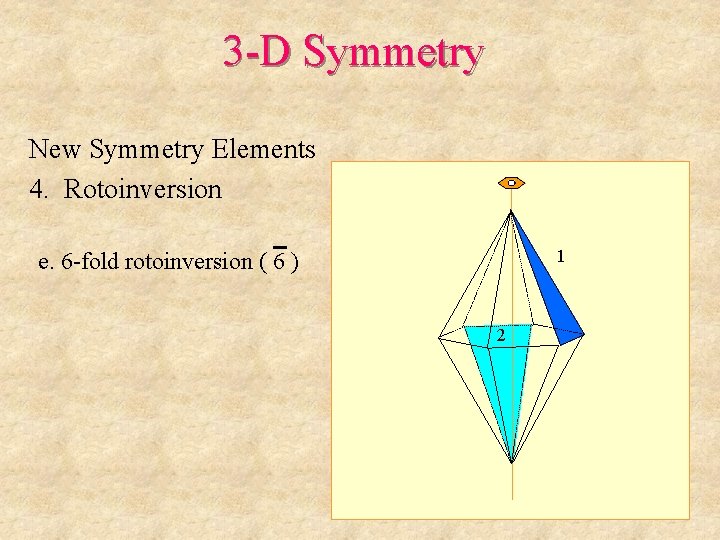
3 -D Symmetry New Symmetry Elements 4. Rotoinversion 1 e. 6 -fold rotoinversion ( 6 ) 2

3 -D Symmetry New Symmetry Elements 4. Rotoinversion 1 e. 6 -fold rotoinversion ( 6 ) 2

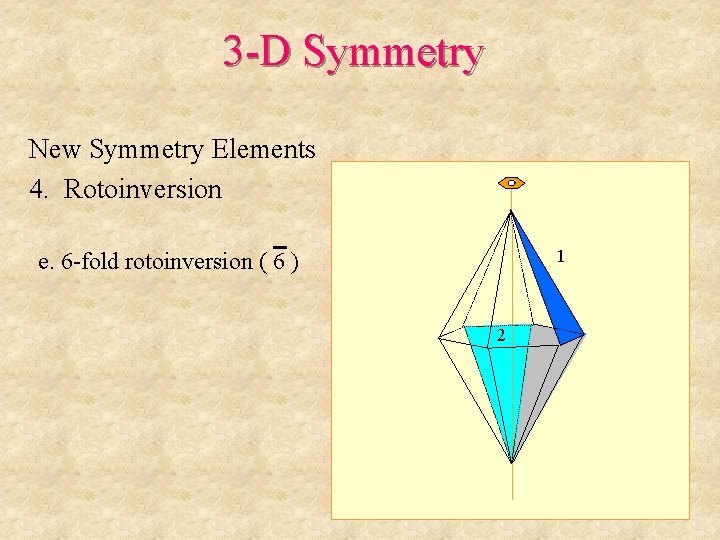
3 -D Symmetry New Symmetry Elements 4. Rotoinversion e. 6 -fold rotoinversion ( 6 ) 1 3 2

3 -D Symmetry New Symmetry Elements 4. Rotoinversion e. 6 -fold rotoinversion ( 6 ) 1 3 2

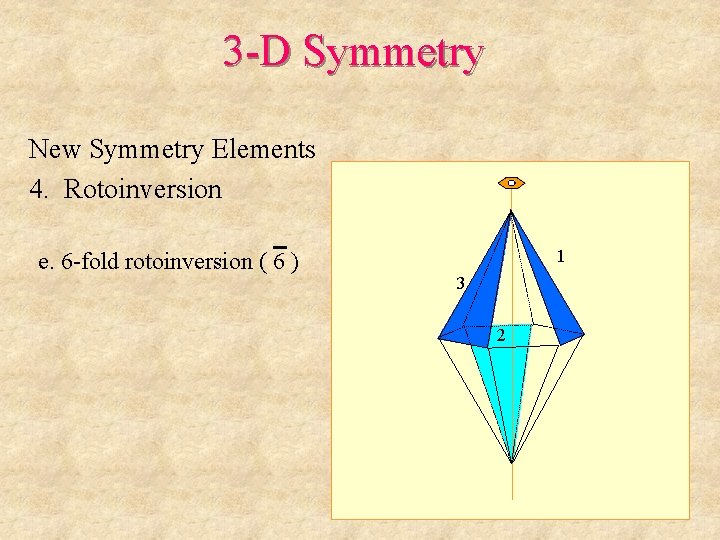
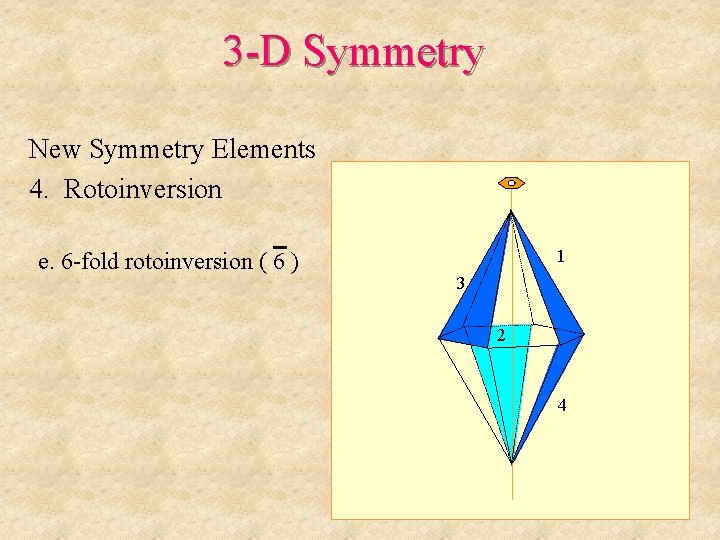
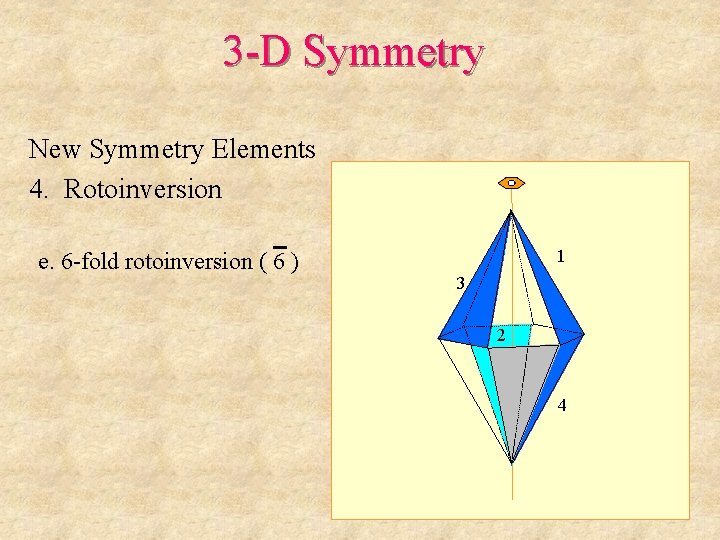
3 -D Symmetry New Symmetry Elements 4. Rotoinversion e. 6 -fold rotoinversion ( 6 ) 1 3 2 4

3 -D Symmetry New Symmetry Elements 4. Rotoinversion e. 6 -fold rotoinversion ( 6 ) 1 3 2 4

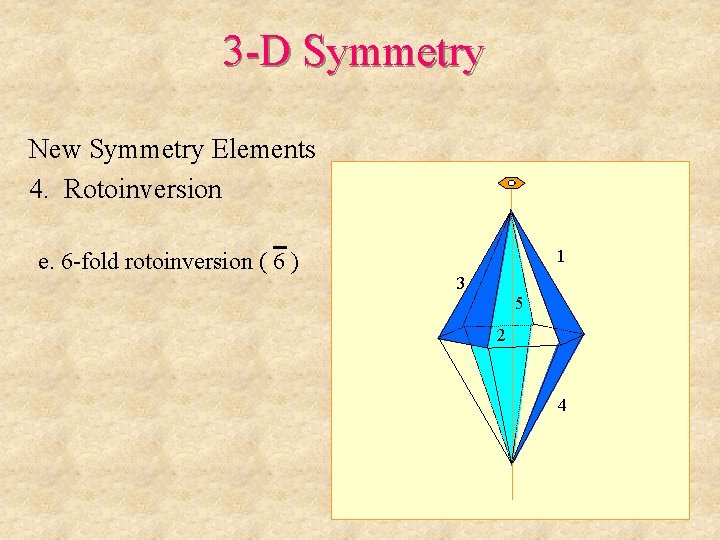
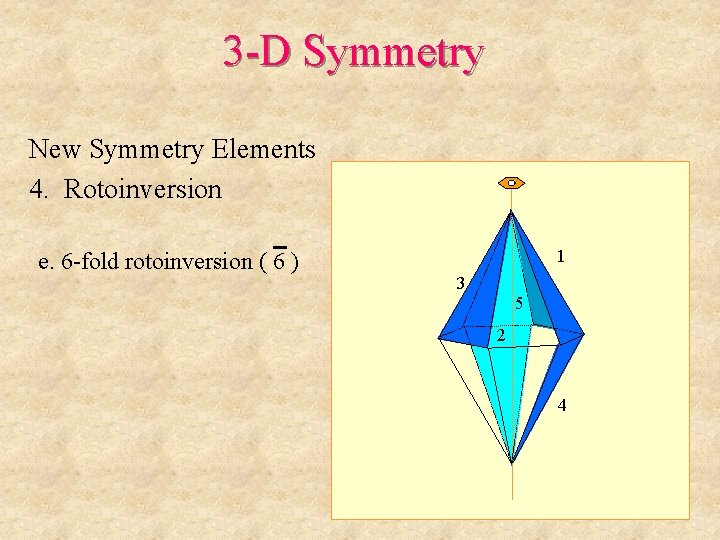
3 -D Symmetry New Symmetry Elements 4. Rotoinversion e. 6 -fold rotoinversion ( 6 ) 1 3 5 2 4

3 -D Symmetry New Symmetry Elements 4. Rotoinversion e. 6 -fold rotoinversion ( 6 ) 1 3 5 2 4

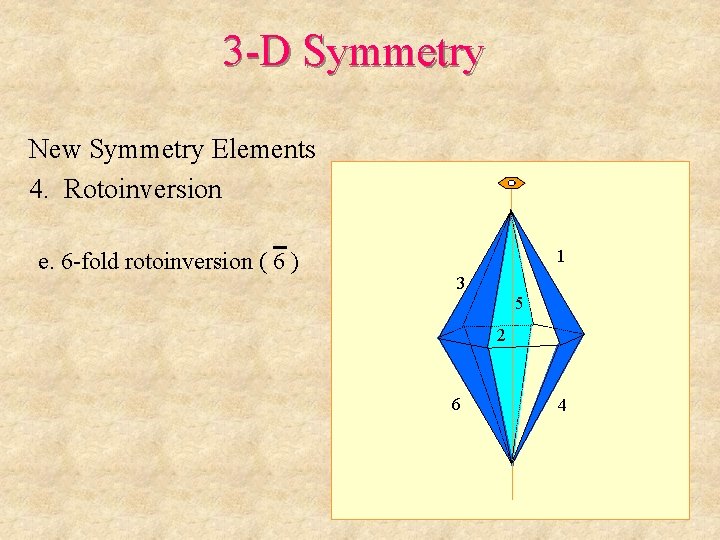
3 -D Symmetry New Symmetry Elements 4. Rotoinversion e. 6 -fold rotoinversion ( 6 ) 1 3 5 2 6 4

3 -D Symmetry New Symmetry Elements 4. Rotoinversion e. 6 -fold rotoinversion ( 6 ) Note: this is the same as a 3 -fold rotation axis perpendicular to a mirror plane Top View (combinations of elements follows)

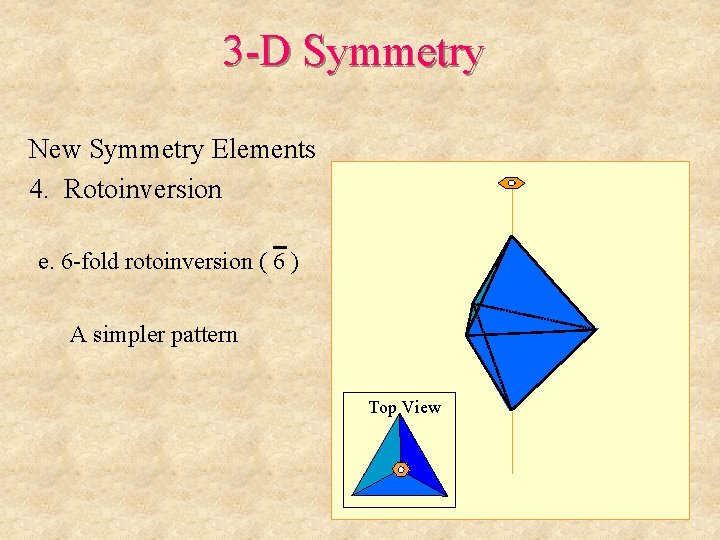
3 -D Symmetry New Symmetry Elements 4. Rotoinversion e. 6 -fold rotoinversion ( 6 ) A simpler pattern Top View

3 -D Symmetry We now have 10 unique 3 -D symmetry operations: 1 2 3 4 6 i m 3 4 6 Combinations of these elements are also possible A complete analysis of symmetry about a point in space requires that we try all possible combinations of these symmetry elements

3 -D Symmetry 3 -D symmetry element combinations a. Rotation axis parallel to a mirror Same as 2 -D 2 || m = 2 mm 3 || m = 3 m, also 4 mm, 6 mm b. Rotation axis mirror 2 m = 2/m 3 m = 3/m, also 4/m, 6/m c. Most other rotations + m are impossible 2 -fold axis at odd angle to mirror? Some cases at 45 o or 30 o are possible, as we shall see

3 -D Symmetry 3 -D symmetry element combinations d. Combinations of rotations 2 + 2 at 90 o 222 (third 2 required from combination) 4 + 2 at 90 o 422 ( “ “ “ ) 6 + 2 at 90 o 622 ( “ “ “ )

3 -D Symmetry As in 2 -D, the number of possible combinations is limited only by incompatibility and redundancy There are only 22 possible unique 3 -D combinations, when combined with the 10 original 3 -D elements yields the 32 3 -D Point Groups

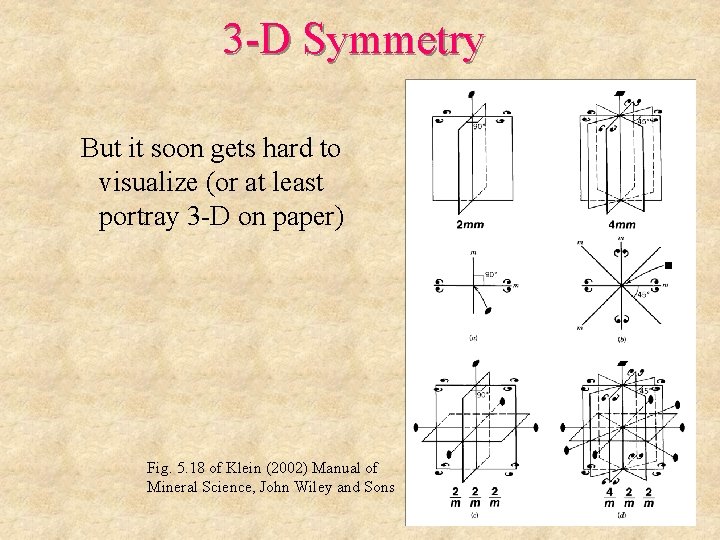
3 -D Symmetry But it soon gets hard to visualize (or at least portray 3 -D on paper) Fig. 5. 18 of Klein (2002) Manual of Mineral Science, John Wiley and Sons

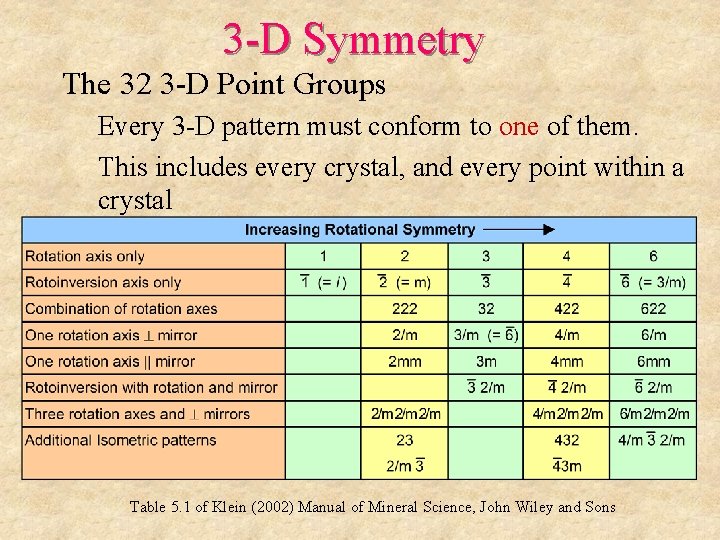
3 -D Symmetry The 32 3 -D Point Groups Every 3 -D pattern must conform to one of them. This includes every crystal, and every point within a crystal Table 5. 1 of Klein (2002) Manual of Mineral Science, John Wiley and Sons

3 -D Symmetry The 32 3 -D Point Groups Regrouped by Crystal System (more later when we consider translations) Table 5. 3 of Klein (2002) Manual of Mineral Science, John Wiley and Sons

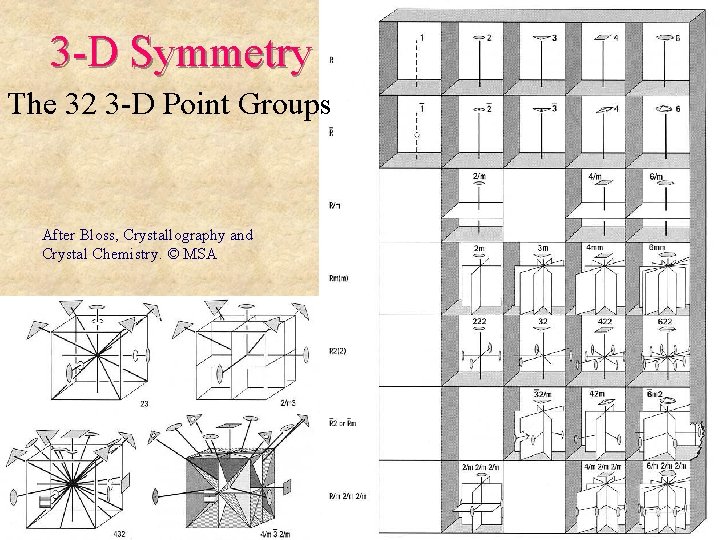
3 -D Symmetry The 32 3 -D Point Groups After Bloss, Crystallography and Crystal Chemistry. © MSA

 Engmae
Engmae Motif berasal dari bahasa inggris yaitu motif yang berarti
Motif berasal dari bahasa inggris yaitu motif yang berarti Draw a motif and create a design using translation symmetry
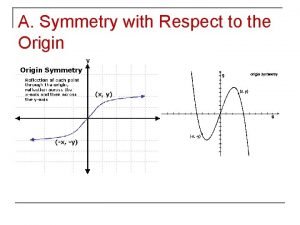
Draw a motif and create a design using translation symmetry Symmetric respect to origin
Symmetric respect to origin Rotational symmetry powerpoint
Rotational symmetry powerpoint Fundamental part 2
Fundamental part 2 Tư thế ngồi viết
Tư thế ngồi viết Gấu đi như thế nào
Gấu đi như thế nào Thẻ vin
Thẻ vin Giọng cùng tên là
Giọng cùng tên là Thể thơ truyền thống
Thể thơ truyền thống Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Hươu thường đẻ mỗi lứa mấy con
Hươu thường đẻ mỗi lứa mấy con Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Diễn thế sinh thái là
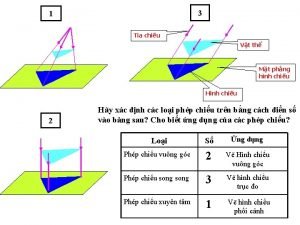
Diễn thế sinh thái là Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Frameset trong html5
Frameset trong html5 Phép trừ bù
Phép trừ bù Lời thề hippocrates
Lời thề hippocrates Tư thế worms-breton
Tư thế worms-breton đại từ thay thế
đại từ thay thế Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Công thức tính độ biến thiên đông lượng
Công thức tính độ biến thiên đông lượng Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Sự nuôi và dạy con của hổ
Sự nuôi và dạy con của hổ Dot
Dot Thế nào là sự mỏi cơ
Thế nào là sự mỏi cơ Bổ thể
Bổ thể Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể độ dài liên kết
độ dài liên kết Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan Alleluia hat len nguoi oi
Alleluia hat len nguoi oi điện thế nghỉ
điện thế nghỉ Một số thể thơ truyền thống
Một số thể thơ truyền thống Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Số nguyên tố là số gì
Số nguyên tố là số gì Fecboak
Fecboak đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới ưu thế lai là gì
ưu thế lai là gì Sơ đồ cơ thể người
Sơ đồ cơ thể người Môn thể thao bắt đầu bằng từ chạy
Môn thể thao bắt đầu bằng từ chạy Tư thế ngồi viết
Tư thế ngồi viết Cái miệng bé xinh thế chỉ nói điều hay thôi
Cái miệng bé xinh thế chỉ nói điều hay thôi Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Cách giải mật thư tọa độ
Cách giải mật thư tọa độ Unit ratio definition
Unit ratio definition The part of a shadow surrounding the darkest part
The part of a shadow surrounding the darkest part Part part whole
Part part whole Part to part variation
Part to part variation Technical description
Technical description Part whole model subtraction
Part whole model subtraction Describe the parts of a front bar
Describe the parts of a front bar Symmetric algorithm
Symmetric algorithm Symmetric vs asymmetric encryption performance
Symmetric vs asymmetric encryption performance Distributed shared memory
Distributed shared memory Symmetric key
Symmetric key A symmetrical top
A symmetrical top Confidentiality using conventional encryption
Confidentiality using conventional encryption Reflexive closure formula
Reflexive closure formula Skew symmetric matrix
Skew symmetric matrix Properties of transpose matrix
Properties of transpose matrix Symmetric difference quotient
Symmetric difference quotient Rigid body
Rigid body Reflexive relation
Reflexive relation Symmetric theorem
Symmetric theorem Eigenvectors of orthogonal matrix
Eigenvectors of orthogonal matrix Symmetric key
Symmetric key What is symmetric difference between two sets
What is symmetric difference between two sets What is poe in geometry
What is poe in geometry Key distribution using asymmetric encryption
Key distribution using asymmetric encryption Simple traversal of udp through nat
Simple traversal of udp through nat Example for reflexive relation
Example for reflexive relation Shared memory vs distributed memory
Shared memory vs distributed memory What is the commutative property of equality
What is the commutative property of equality Searchable symmetric encryption
Searchable symmetric encryption Frequency table
Frequency table Symmetric key
Symmetric key Searchable symmetric encryption
Searchable symmetric encryption Which symmetric block cipher supersedes blowfish
Which symmetric block cipher supersedes blowfish How atoms are in observable
How atoms are in observable Symmetric shared memory architecture
Symmetric shared memory architecture A long jumper leaves the ground at an angle of 45
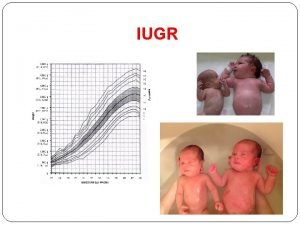
A long jumper leaves the ground at an angle of 45 Asymmetrical iugr baby images
Asymmetrical iugr baby images Determine if function is even or odd
Determine if function is even or odd Java symmetric encryption
Java symmetric encryption Transitive property
Transitive property Reciprocal and quotient identities
Reciprocal and quotient identities Encipherment
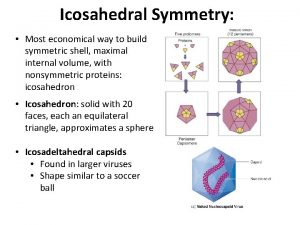
Encipherment Icosadeltahedral
Icosadeltahedral Half wave odd symmetry
Half wave odd symmetry Identify the distribution shapes that are symmetric
Identify the distribution shapes that are symmetric