Numerical Measures Numerical Measures Measures of Central Tendency





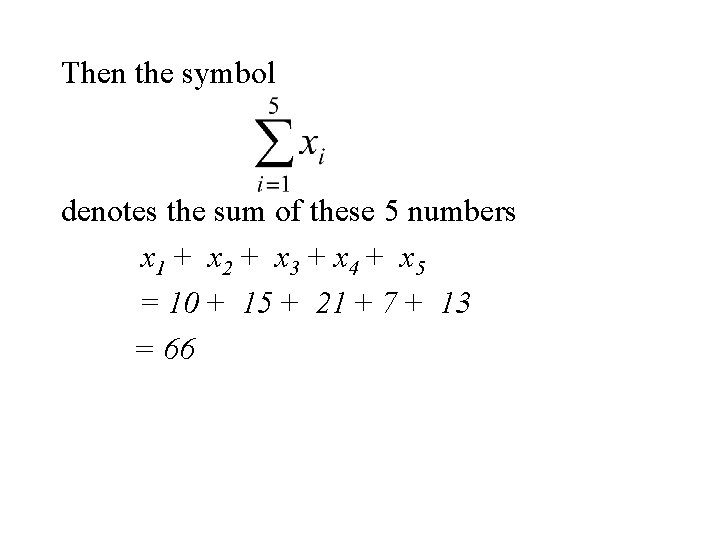


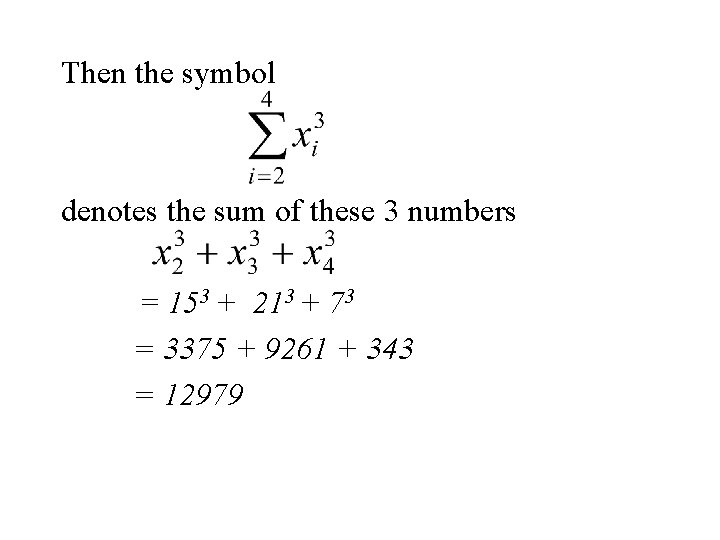

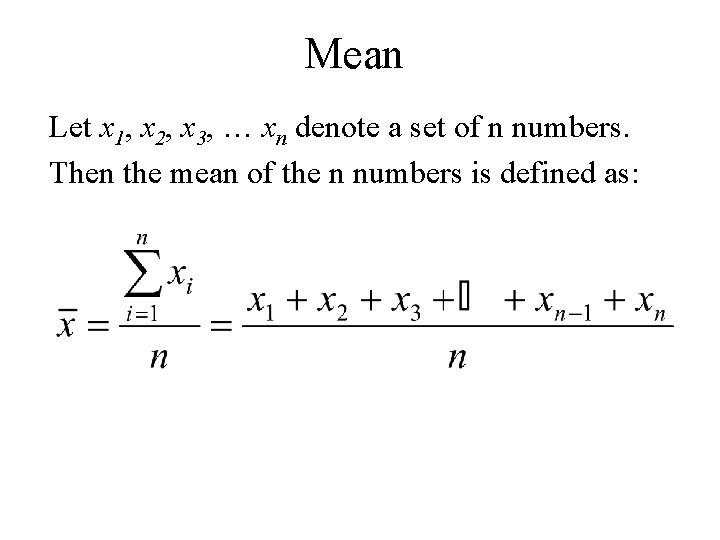

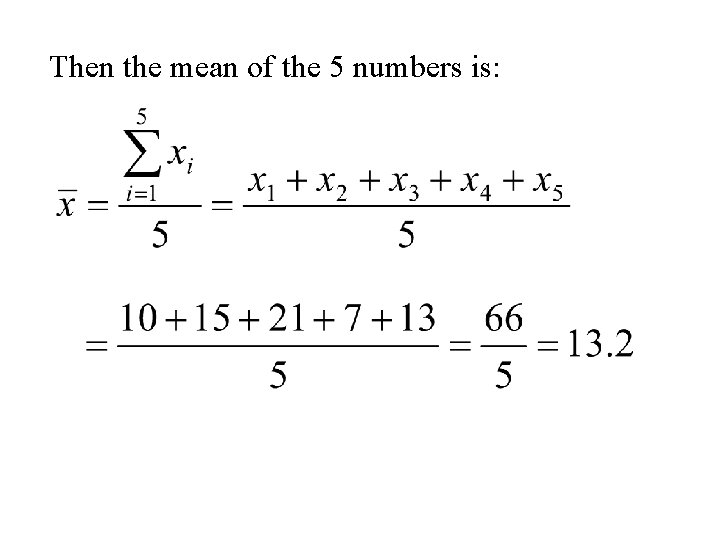










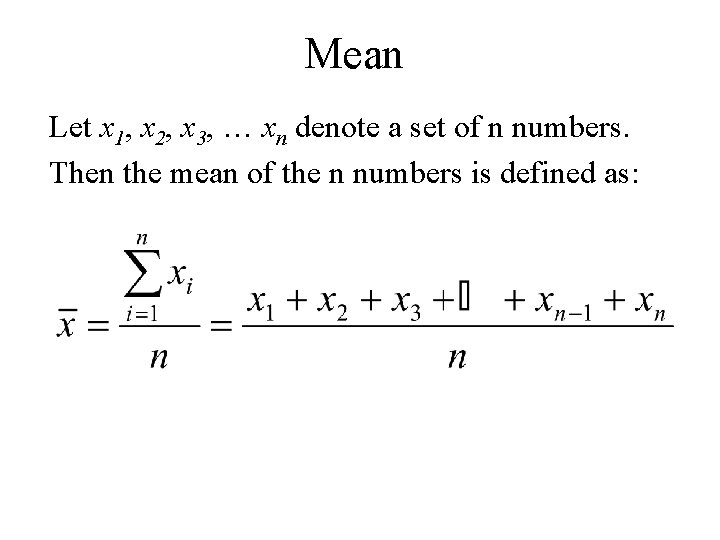










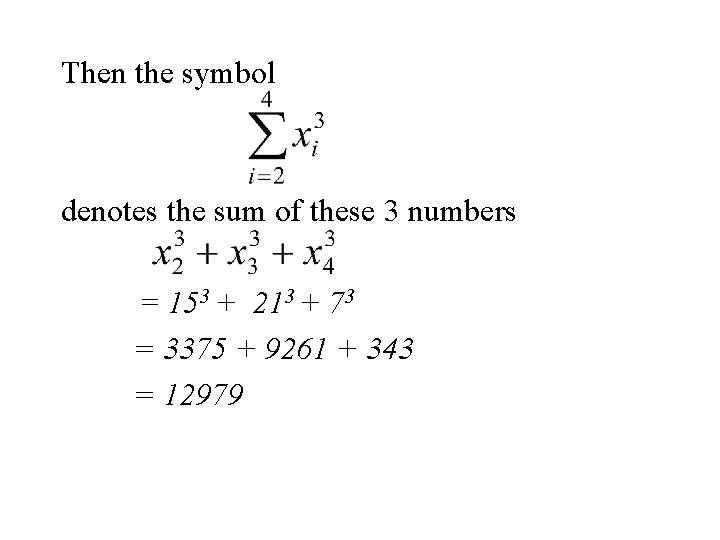
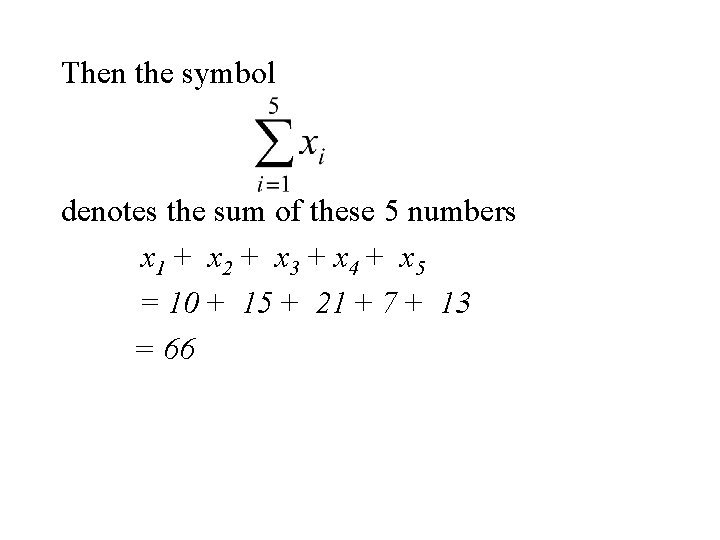

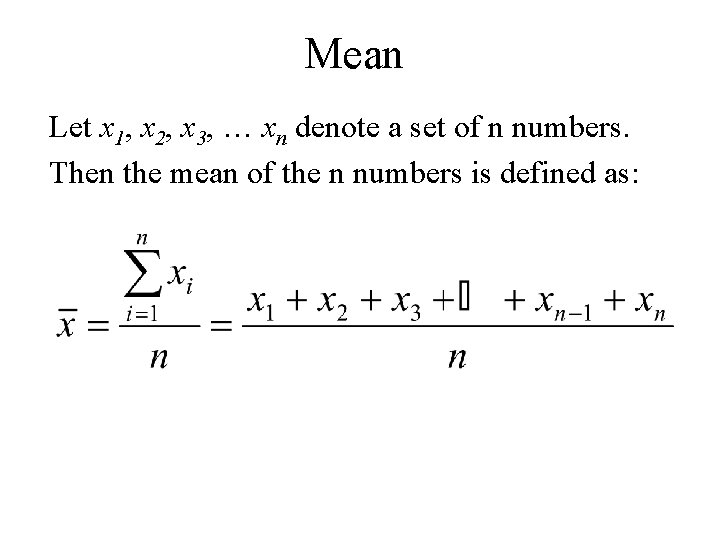

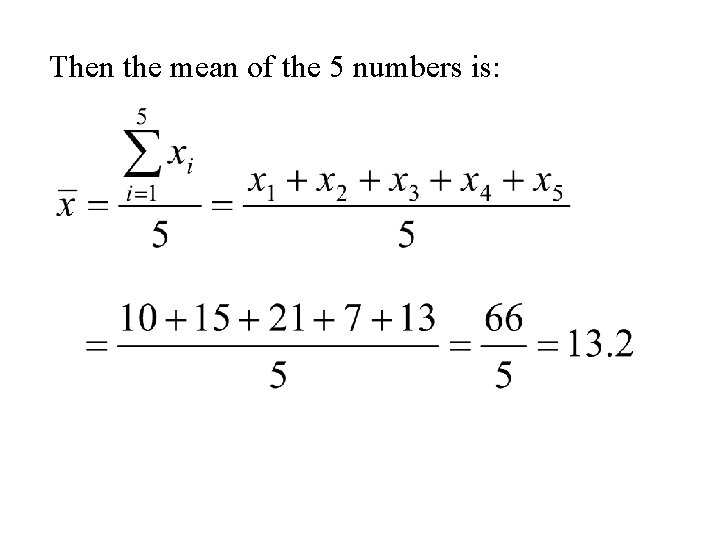



























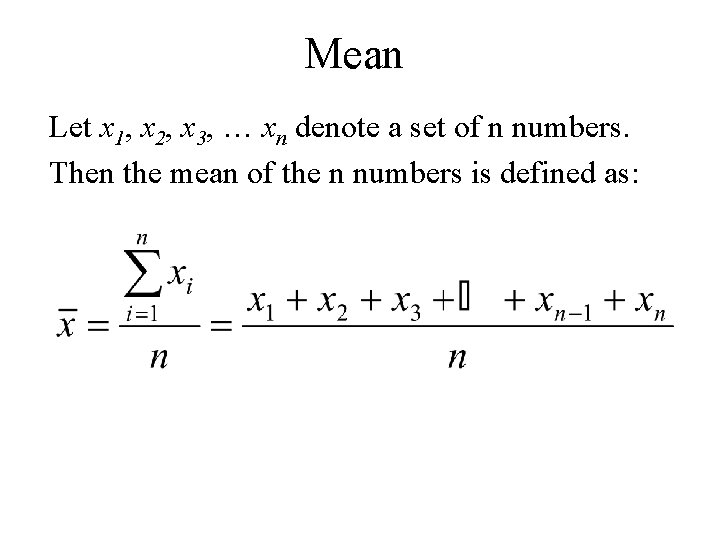














- Slides: 128

Numerical Measures

Numerical Measures • • Measures of Central Tendency (Location) Measures of Non Central Location Measure of Variability (Dispersion, Spread) Measures of Shape

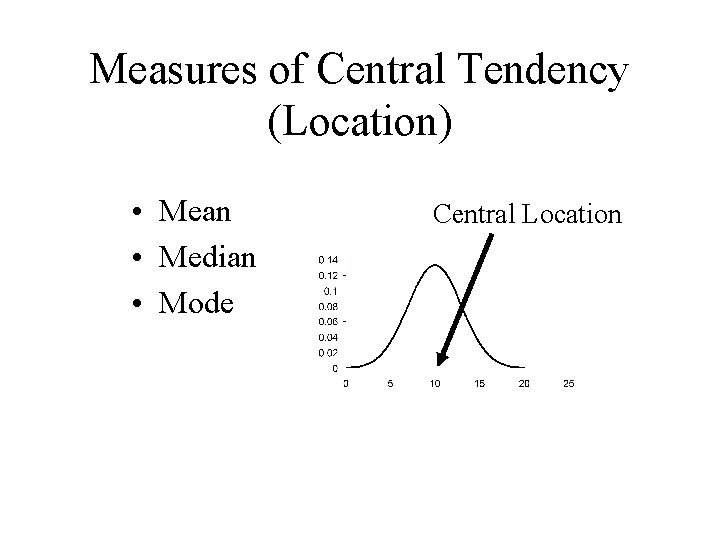
Measures of Central Tendency (Location) • Mean • Median • Mode Central Location

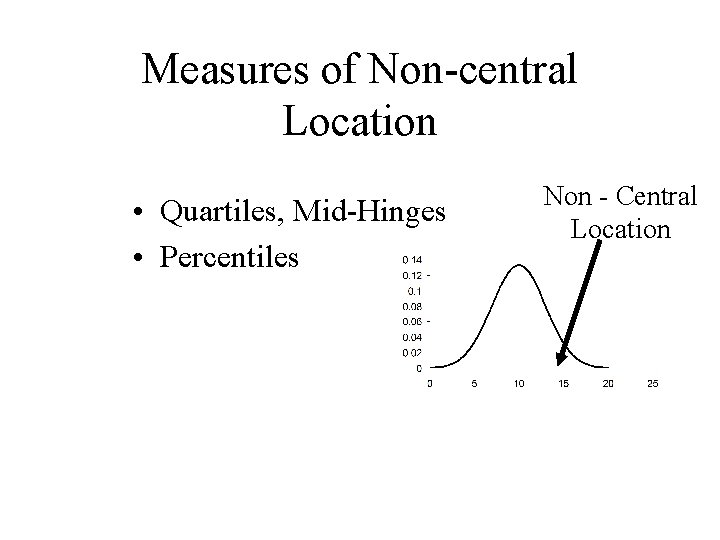
Measures of Non-central Location • Quartiles, Mid-Hinges • Percentiles Non - Central Location

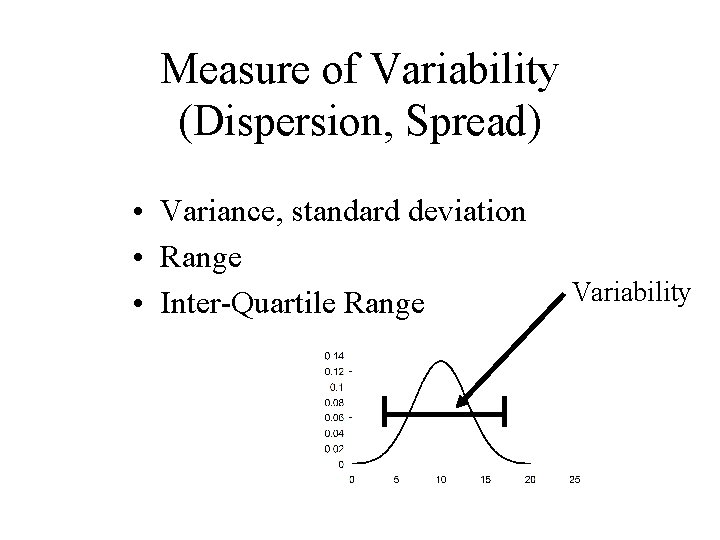
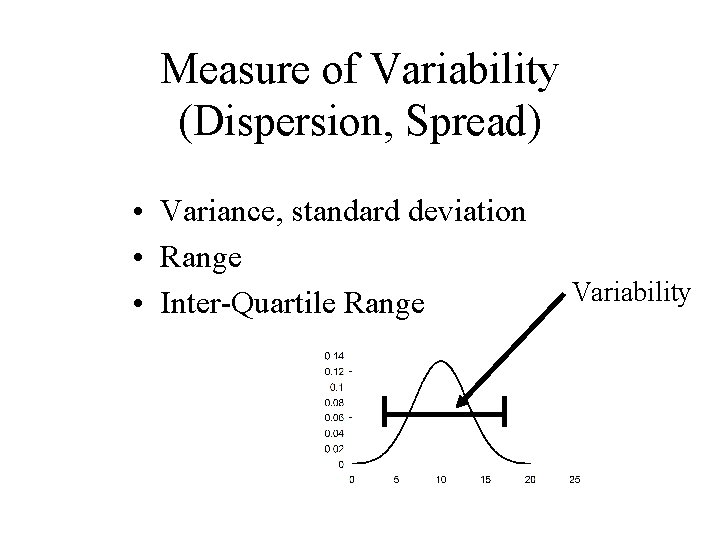
Measure of Variability (Dispersion, Spread) • Variance, standard deviation • Range • Inter-Quartile Range Variability

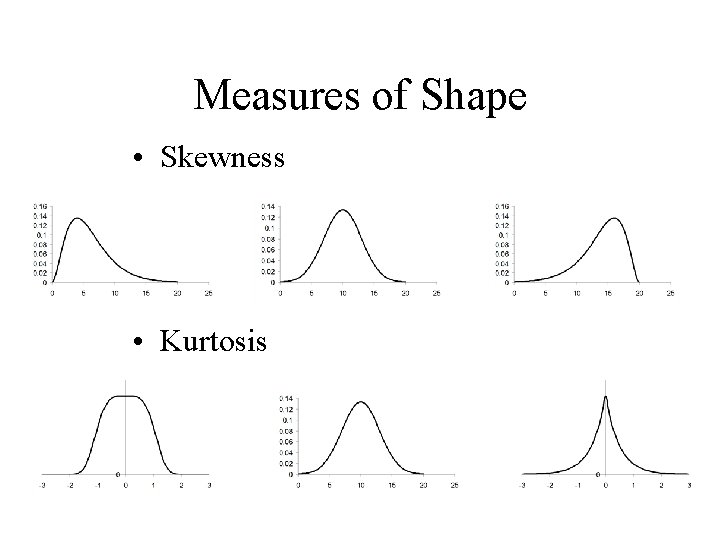
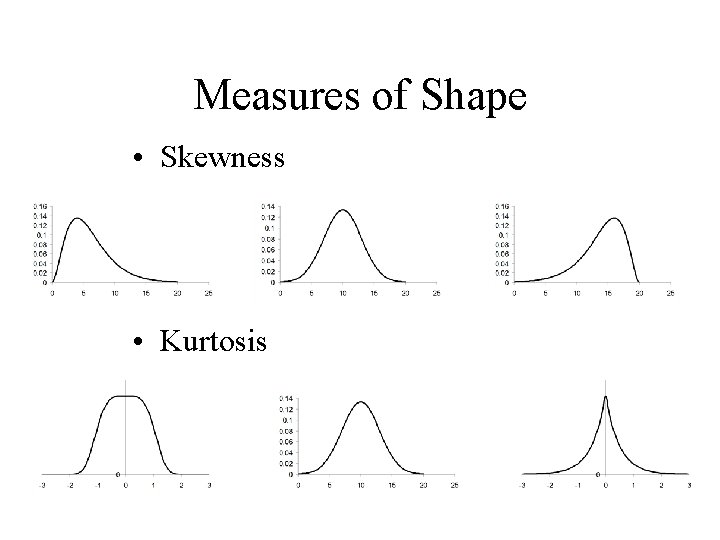
Measures of Shape • Skewness • Kurtosis

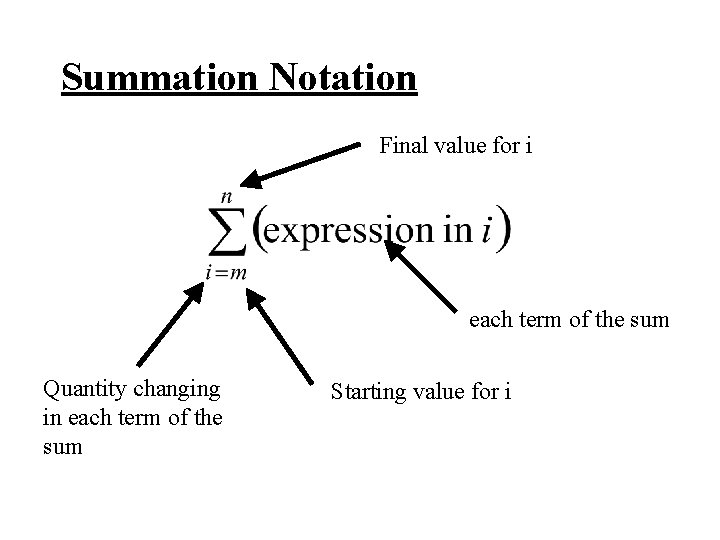
Summation Notation

Summation Notation Let x 1, x 2, x 3, … xn denote a set of n numbers. Then the symbol denotes the sum of these n numbers x 1 + x 2 + x 3 + …+ xn

Example Let x 1, x 2, x 3, x 4, x 5 denote a set of 5 denote the set of numbers in the following table. i 1 2 3 4 5 xi 10 15 21 7 13
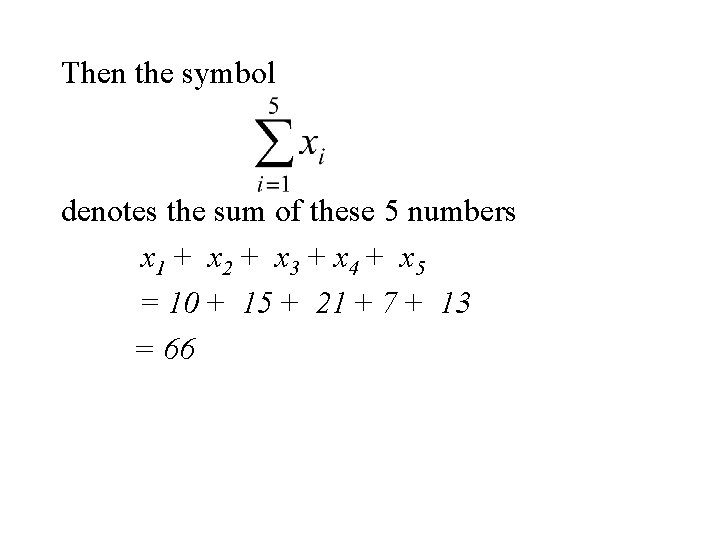
Then the symbol denotes the sum of these 5 numbers x 1 + x 2 + x 3 + x 4 + x 5 = 10 + 15 + 21 + 7 + 13 = 66

Meaning of parts of summation notation Final value for i each term of the sum Quantity changing in each term of the sum Starting value for i

Example Again let x 1, x 2, x 3, x 4, x 5 denote a set of 5 denote the set of numbers in the following table. i 1 2 3 4 5 xi 10 15 21 7 13
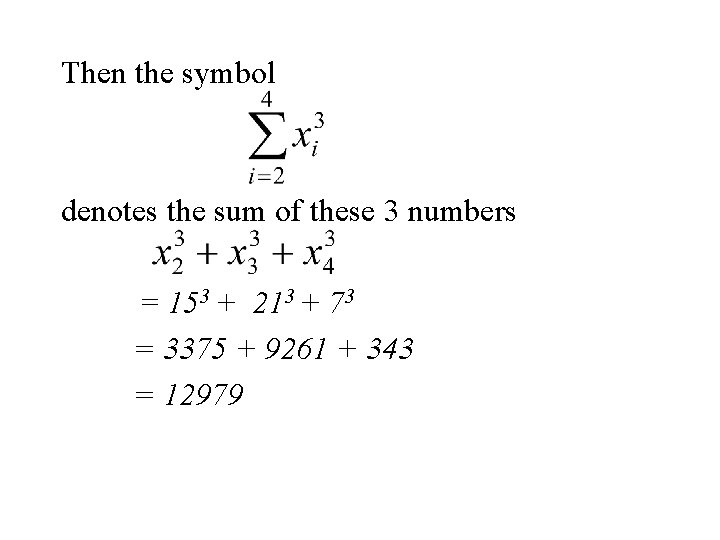
Then the symbol denotes the sum of these 3 numbers = 153 + 213 + 73 = 3375 + 9261 + 343 = 12979

Measures of Central Location (Mean)
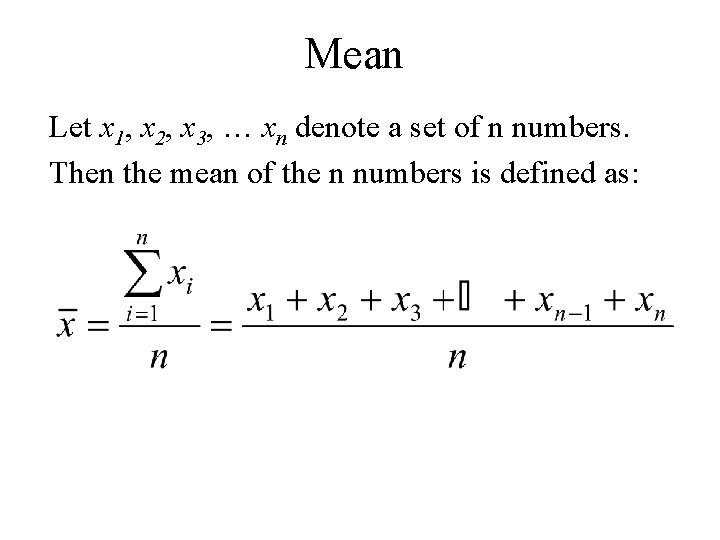
Mean Let x 1, x 2, x 3, … xn denote a set of n numbers. Then the mean of the n numbers is defined as:

Example Again let x 1, x 2, x 3, x 4, x 5 denote a set of 5 denote the set of numbers in the following table. i 1 2 3 4 5 xi 10 15 21 7 13
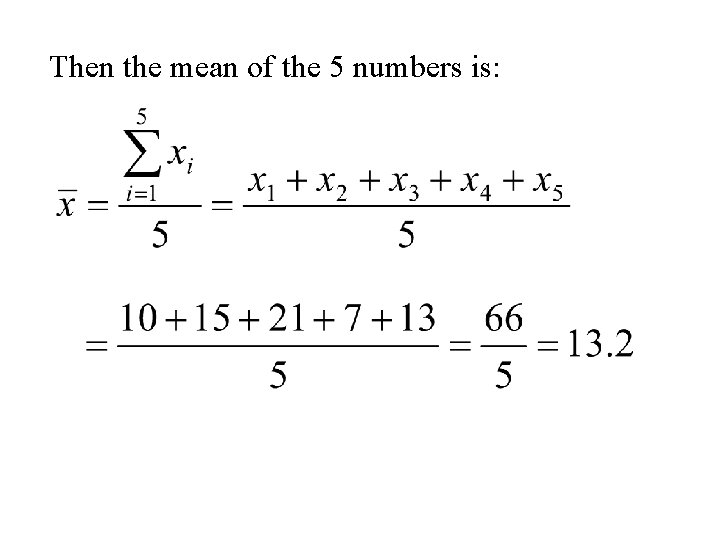
Then the mean of the 5 numbers is:

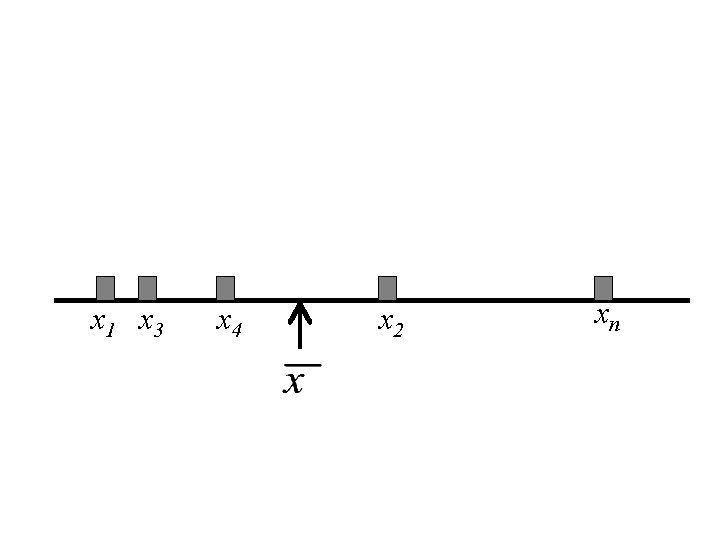
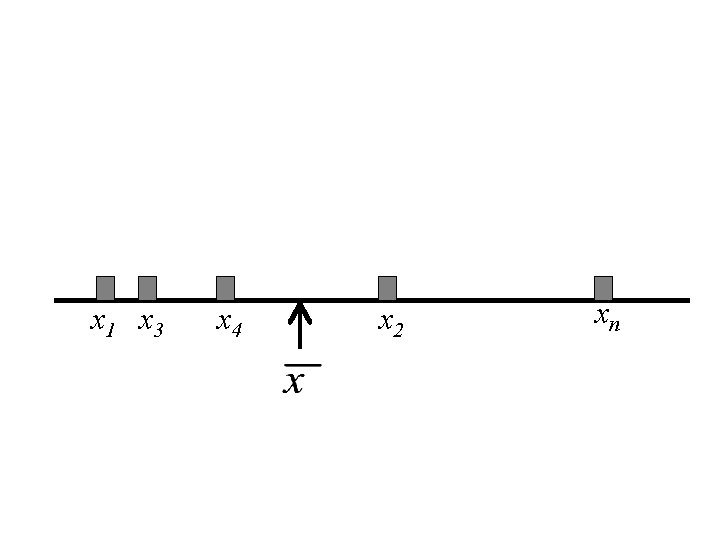
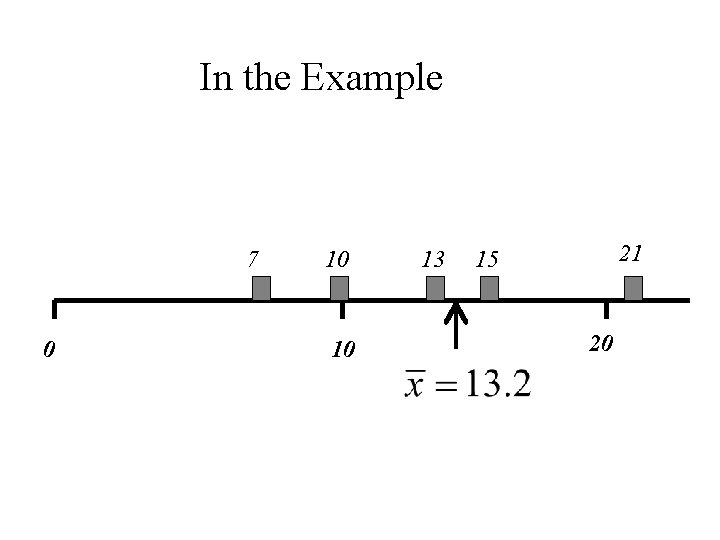
Interpretation of the Mean Let x 1, x 2, x 3, … xn denote a set of n numbers. Then the mean, , is the centre of gravity of those the n numbers. That is if we drew a horizontal line and placed a weight of one at each value of xi , then the balancing point of that system of mass is at the point.

x 1 x 3 x 4 x 2 xn

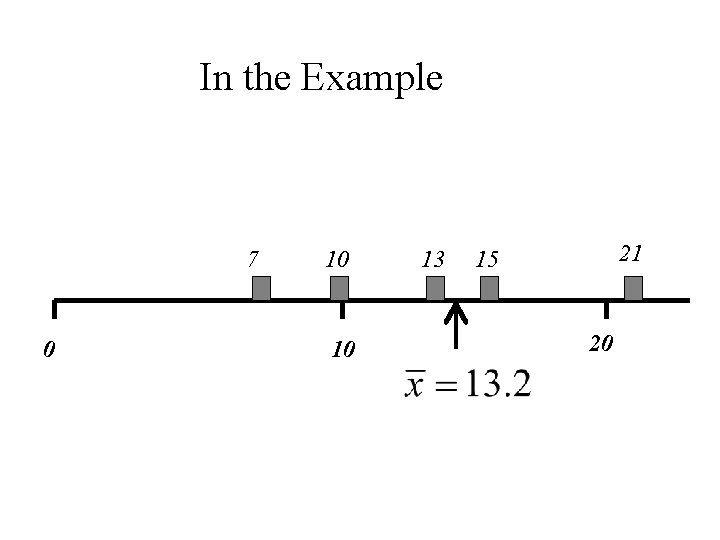
In the Example 7 0 10 10 13 21 15 20

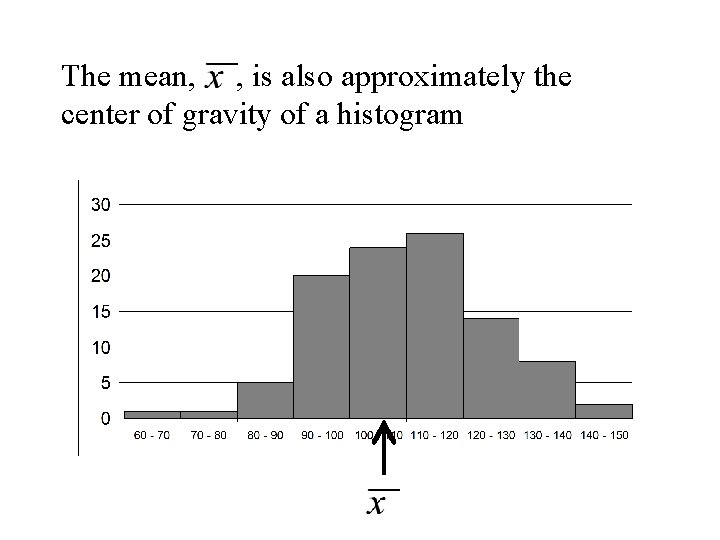
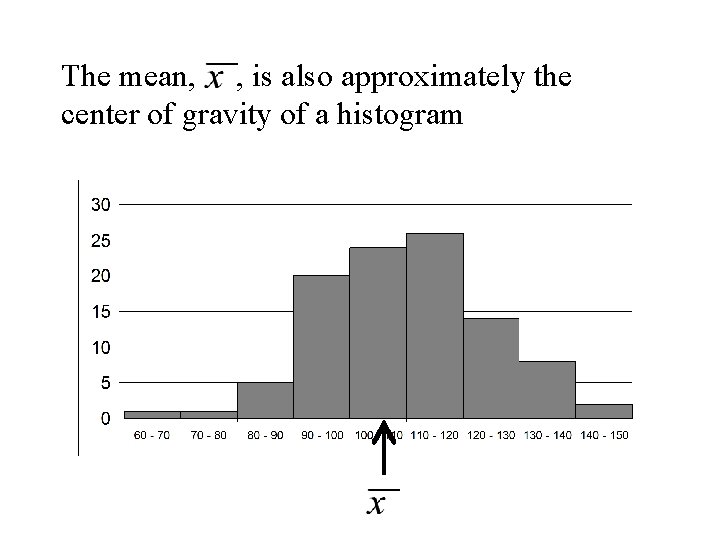
The mean, , is also approximately the center of gravity of a histogram

Measures of Central Location (Median)

The Median Let x 1, x 2, x 3, … xn denote a set of n numbers. Then the median of the n numbers is defined as the number that splits the numbers into two equal parts. To evaluate the median we arrange the numbers in increasing order.

If the number of observations is odd there will be one observation in the middle. This number is the median. If the number of observations is even there will be two middle observations. The median is the average of these two observations

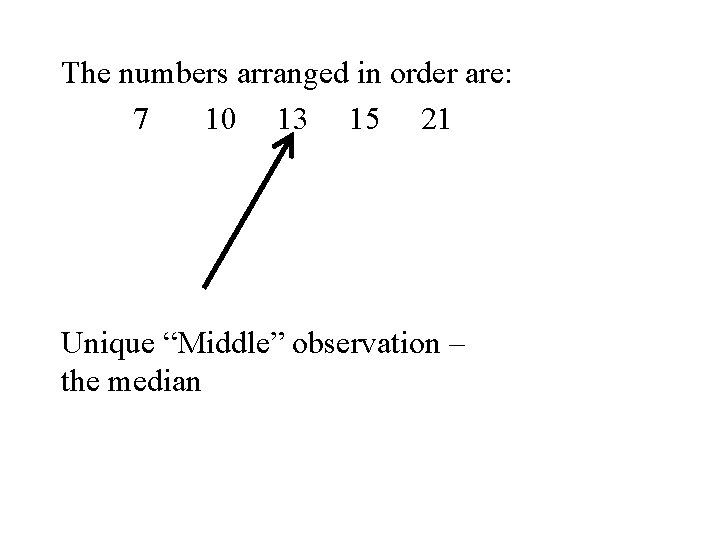
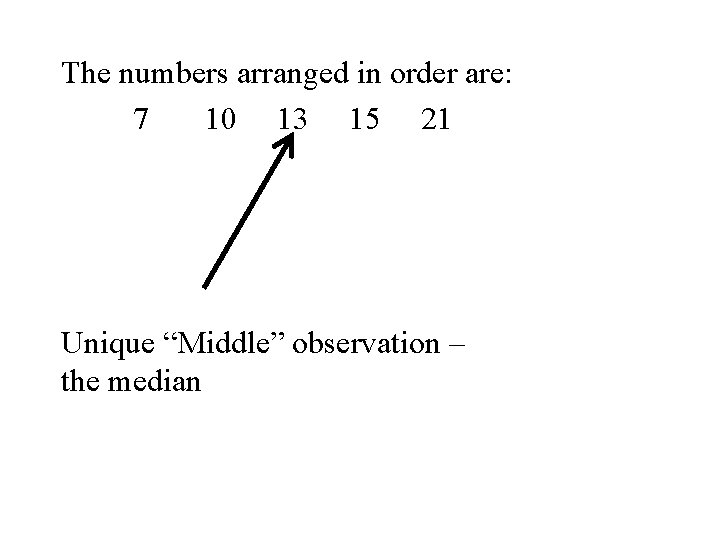
Example Again let x 1, x 2, x 3 , x 4, x 5 denote a set of 5 denote the set of numbers in the following table. i 1 2 3 4 5 xi 10 15 21 7 13

The numbers arranged in order are: 7 10 13 15 21 Unique “Middle” observation – the median

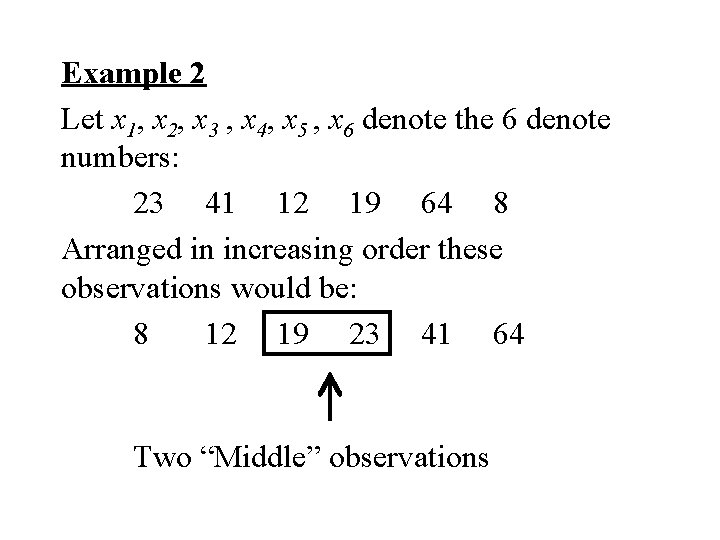
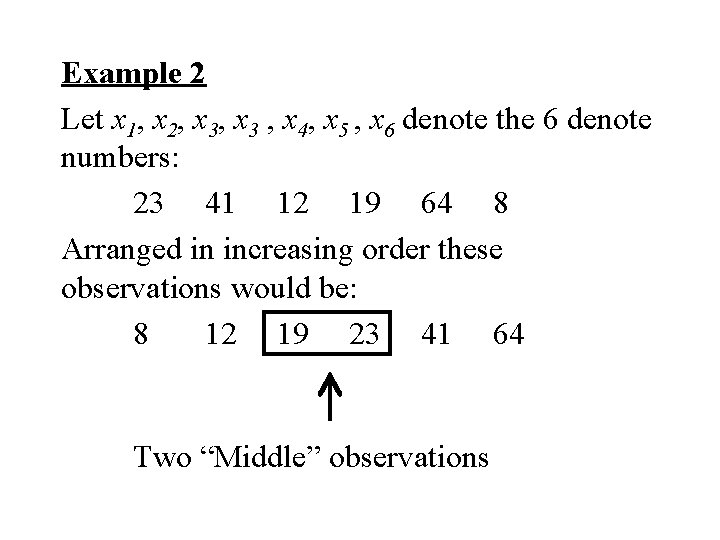
Example 2 Let x 1, x 2, x 3 , x 4, x 5 , x 6 denote the 6 denote numbers: 23 41 12 19 64 8 Arranged in increasing order these observations would be: 8 12 19 23 41 64 Two “Middle” observations

Median = average of two “middle” observations =

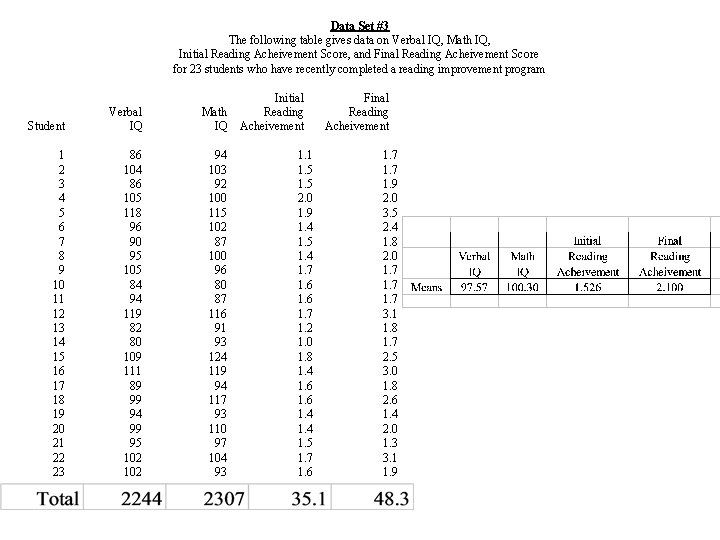
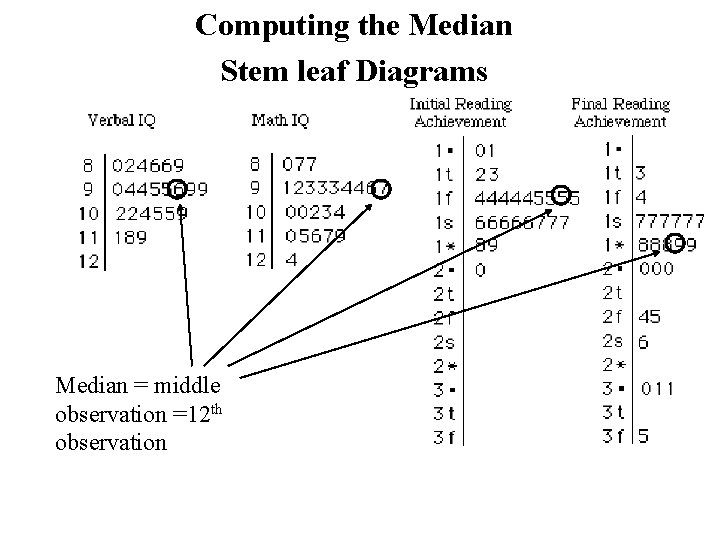
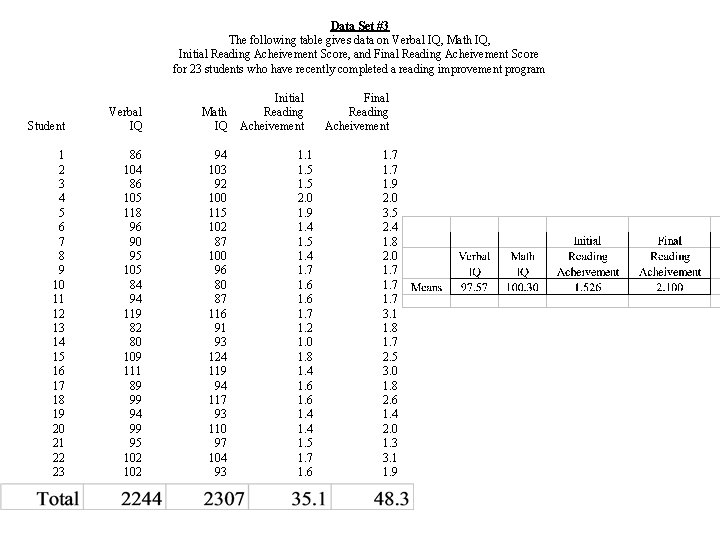
Example The data on N = 23 students Variables • Verbal IQ • Math IQ • Initial Reading Achievement Score • Final Reading Achievement Score

Data Set #3 The following table gives data on Verbal IQ, Math IQ, Initial Reading Acheivement Score, and Final Reading Acheivement Score for 23 students who have recently completed a reading improvement program Student Verbal IQ Math IQ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 86 104 86 105 118 96 90 95 105 84 94 119 82 80 109 111 89 99 94 99 95 102 94 103 92 100 115 102 87 100 96 80 87 116 91 93 124 119 94 117 93 110 97 104 93 Initial Reading Acheivement 1. 1 1. 5 2. 0 1. 9 1. 4 1. 5 1. 4 1. 7 1. 6 1. 7 1. 2 1. 0 1. 8 1. 4 1. 6 1. 4 1. 5 1. 7 1. 6 Final Reading Acheivement 1. 7 1. 9 2. 0 3. 5 2. 4 1. 8 2. 0 1. 7 3. 1 1. 8 1. 7 2. 5 3. 0 1. 8 2. 6 1. 4 2. 0 1. 3 3. 1 1. 9

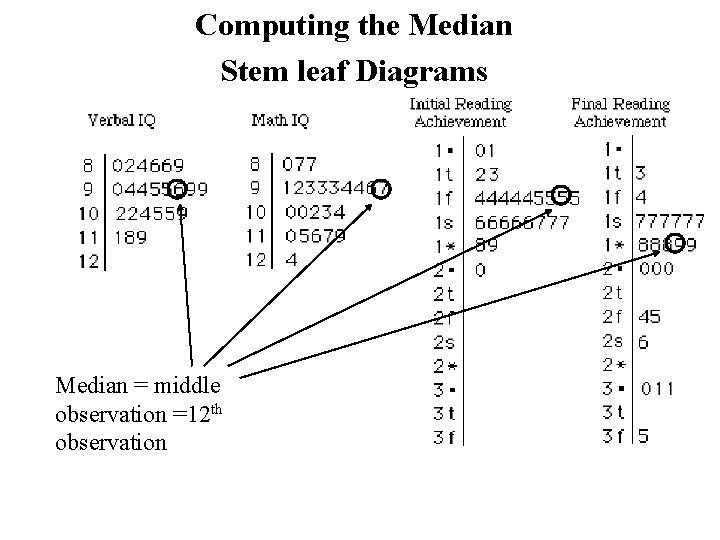
Computing the Median Stem leaf Diagrams Median = middle observation =12 th observation

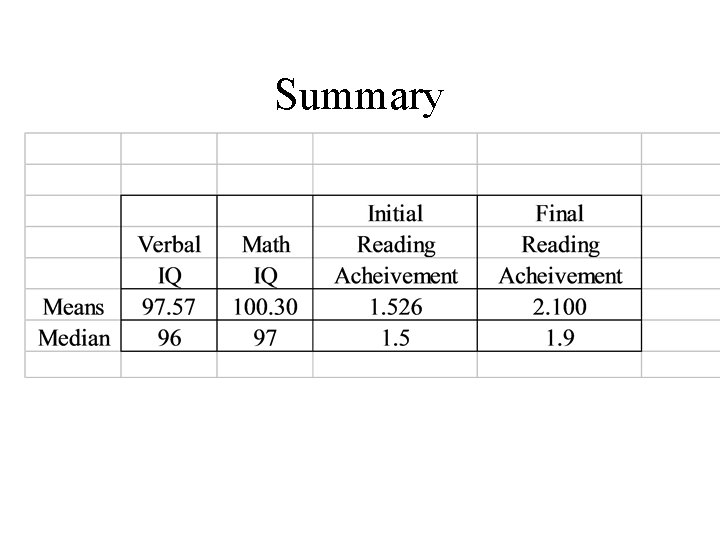
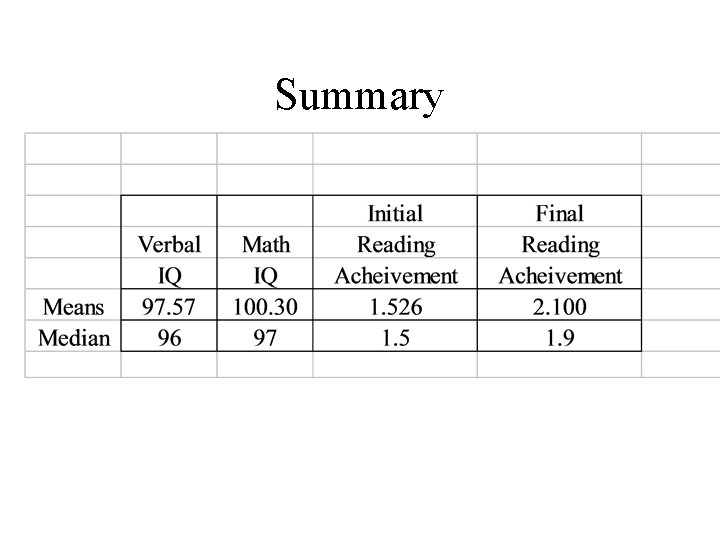
Summary

Numerical Measures

Numerical Measures • • Measures of Central Tendency (Location) Measures of Non Central Location Measure of Variability (Dispersion, Spread) Measures of Shape

Measures of Central Tendency (Location) • Mean • Median • Mode Central Location

Measures of Non-central Location • Quartiles, Mid-Hinges • Percentiles Non - Central Location

Measure of Variability (Dispersion, Spread) • Variance, standard deviation • Range • Inter-Quartile Range Variability

Measures of Shape • Skewness • Kurtosis

Measures of Central Location Mean Median
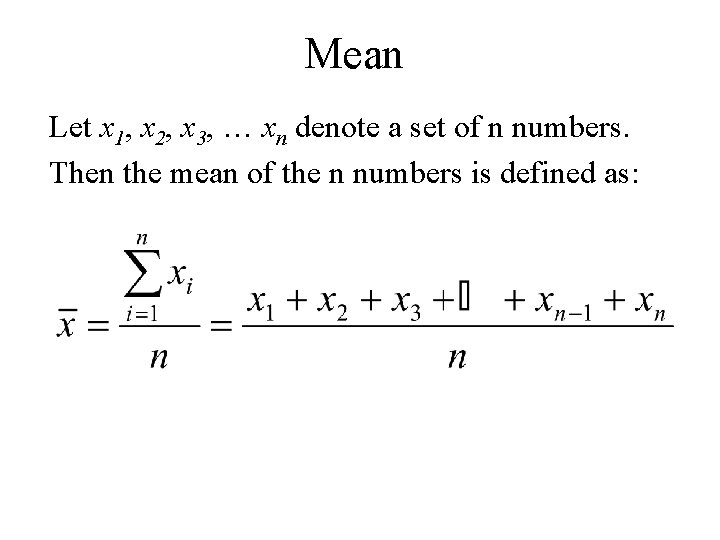
Mean Let x 1, x 2, x 3, … xn denote a set of n numbers. Then the mean of the n numbers is defined as:

The Median Let x 1, x 2, x 3, … xn denote a set of n numbers. Then the median of the n numbers is defined as the number that splits the numbers into two equal parts. To evaluate the median we arrange the numbers in increasing order.

If the number of observations is odd there will be one observation in the middle. This number is the median. If the number of observations is even there will be two middle observations. The median is the average of these two observations

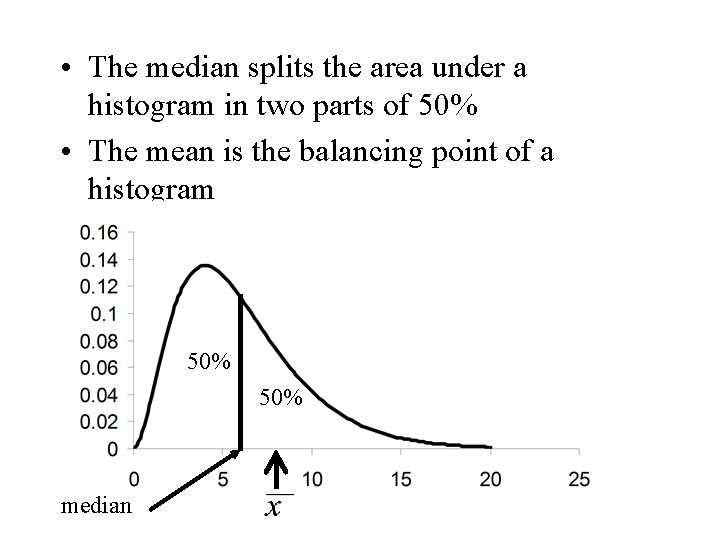
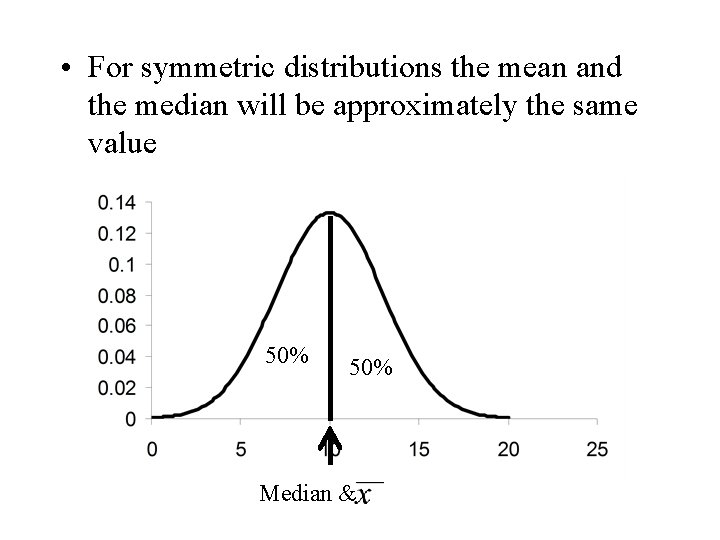
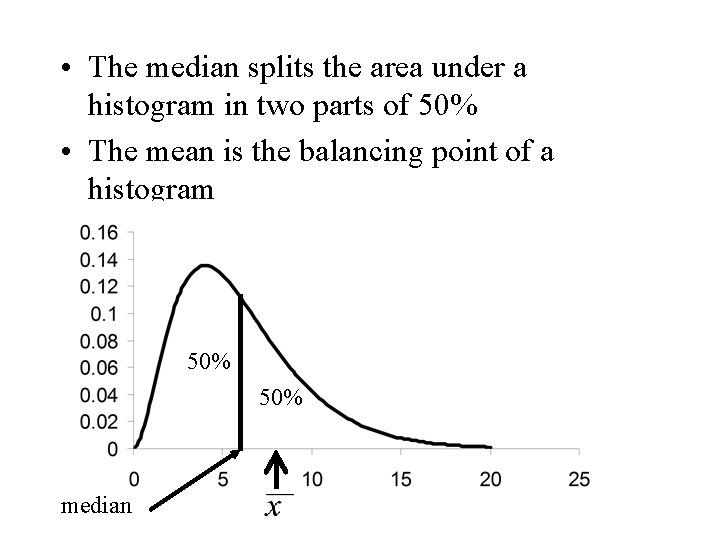
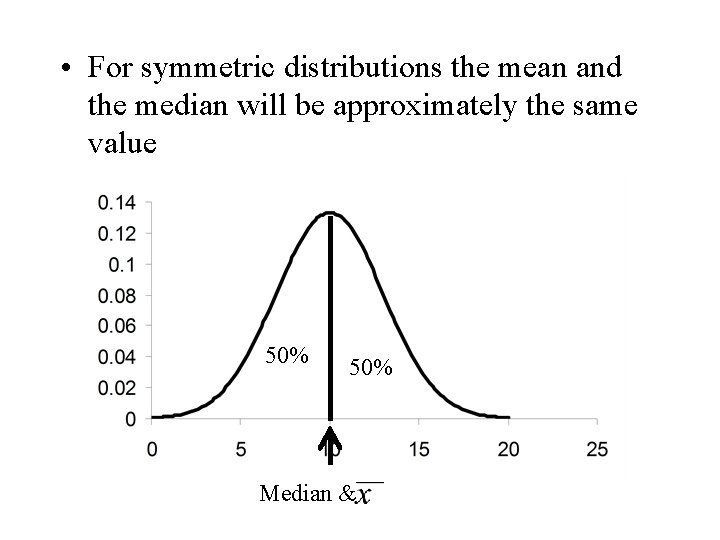
Some Comments • The mean is the centre of gravity of a set of observations. The balancing point. • The median splits the obsevations equally in two parts of approximately 50%

• The median splits the area under a histogram in two parts of 50% • The mean is the balancing point of a histogram 50% median

• For symmetric distributions the mean and the median will be approximately the same value 50% Median &

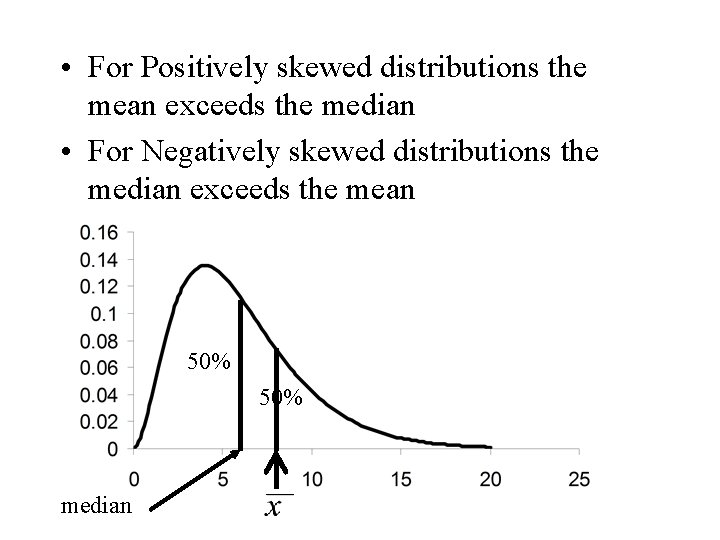
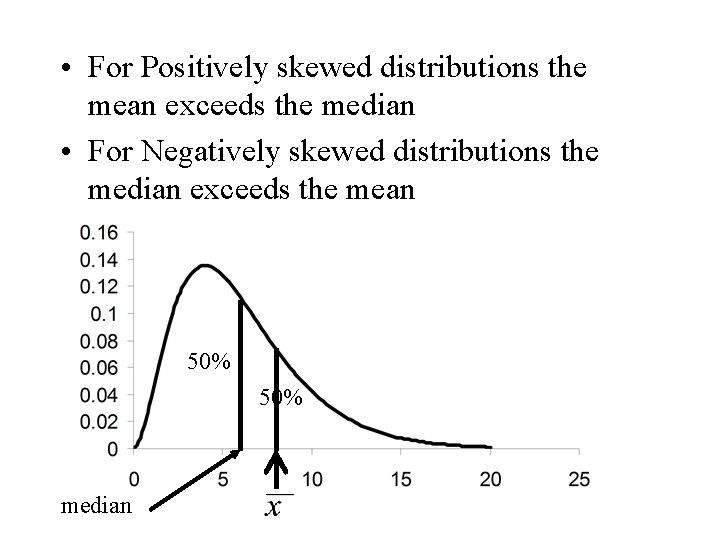
• For Positively skewed distributions the mean exceeds the median • For Negatively skewed distributions the median exceeds the mean 50% median

• An outlier is a “wild” observation in the data • Outliers occur because – of errors (typographical and computational) – Extreme cases in the population

• The mean is altered to a significant degree by the presence of outliers • Outliers have little effect on the value of the median • This is a reason for using the median in place of the mean as a measure of central location • Alternatively the mean is the best measure of central location when the data is Normally distributed (Bell-shaped)

Review

Summarizing Data Graphical Methods

Histogram Stem-Leaf Diagram Grouped Freq Table

Numerical Measures • • Measures of Central Tendency (Location) Measures of Non Central Location Measure of Variability (Dispersion, Spread) Measures of Shape The objective is to reduce the data to a small number of values that completely describe the data and certain aspects of the data.

Summation Notation Final value for i each term of the sum Quantity changing in each term of the sum Starting value for i

Example Let x 1, x 2, x 3, x 4, x 5 denote a set of 5 denote the set of numbers in the following table. i 1 2 3 4 5 xi 10 15 21 7 13
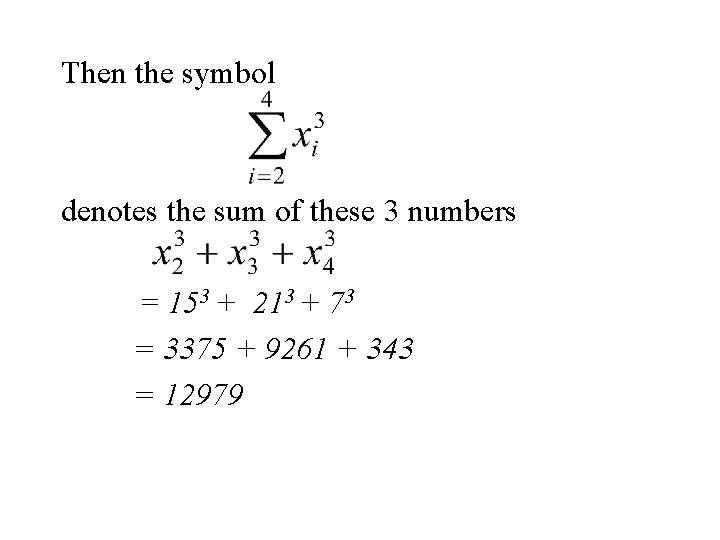
Then the symbol denotes the sum of these 3 numbers = 153 + 213 + 73 = 3375 + 9261 + 343 = 12979
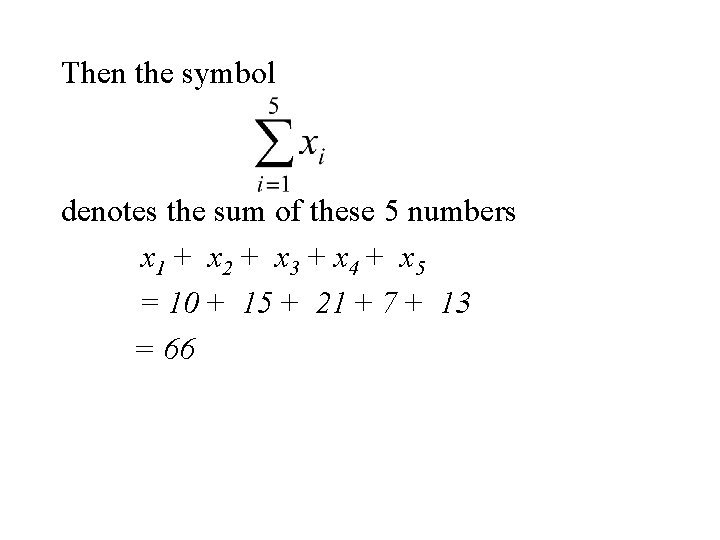
Then the symbol denotes the sum of these 5 numbers x 1 + x 2 + x 3 + x 4 + x 5 = 10 + 15 + 21 + 7 + 13 = 66

Measures of Central Location (Mean)
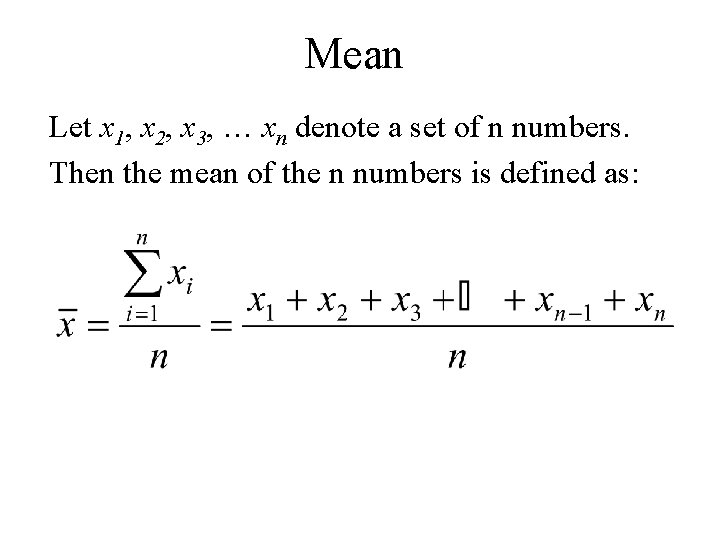
Mean Let x 1, x 2, x 3, … xn denote a set of n numbers. Then the mean of the n numbers is defined as:

Example Again let x 1, x 2, x 3 , x 4, x 5 denote a set of 5 denote the set of numbers in the following table. i 1 2 3 4 5 xi 10 15 21 7 13
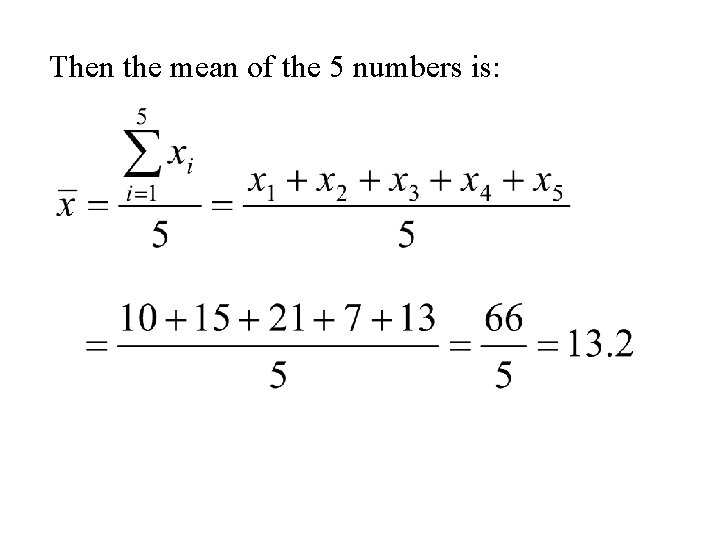
Then the mean of the 5 numbers is:

Interpretation of the Mean Let x 1, x 2, x 3, … xn denote a set of n numbers. Then the mean, , is the centre of gravity of those the n numbers. That is if we drew a horizontal line and placed a weight of one at each value of xi , then the balancing point of that system of mass is at the point.

x 1 x 3 x 4 x 2 xn

In the Example 7 0 10 10 13 21 15 20

The mean, , is also approximately the center of gravity of a histogram

The Median Let x 1, x 2, x 3, … xn denote a set of n numbers. Then the median of the n numbers is defined as the number that splits the numbers into two equal parts. To evaluate the median we arrange the numbers in increasing order.

If the number of observations is odd there will be one observation in the middle. This number is the median. If the number of observations is even there will be two middle observations. The median is the average of these two observations

Example Again let x 1, x 2, x 3 , x 4, x 5 denote a set of 5 denote the set of numbers in the following table. i 1 2 3 4 5 xi 10 15 21 7 13

The numbers arranged in order are: 7 10 13 15 21 Unique “Middle” observation – the median

Example 2 Let x 1, x 2, x 3 , x 4, x 5 , x 6 denote the 6 denote numbers: 23 41 12 19 64 8 Arranged in increasing order these observations would be: 8 12 19 23 41 64 Two “Middle” observations

Median = average of two “middle” observations =

Example The data on N = 23 students Variables • Verbal IQ • Math IQ • Initial Reading Achievement Score • Final Reading Achievement Score

Data Set #3 The following table gives data on Verbal IQ, Math IQ, Initial Reading Acheivement Score, and Final Reading Acheivement Score for 23 students who have recently completed a reading improvement program Student Verbal IQ Math IQ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 86 104 86 105 118 96 90 95 105 84 94 119 82 80 109 111 89 99 94 99 95 102 94 103 92 100 115 102 87 100 96 80 87 116 91 93 124 119 94 117 93 110 97 104 93 Initial Reading Acheivement 1. 1 1. 5 2. 0 1. 9 1. 4 1. 5 1. 4 1. 7 1. 6 1. 7 1. 2 1. 0 1. 8 1. 4 1. 6 1. 4 1. 5 1. 7 1. 6 Final Reading Acheivement 1. 7 1. 9 2. 0 3. 5 2. 4 1. 8 2. 0 1. 7 3. 1 1. 8 1. 7 2. 5 3. 0 1. 8 2. 6 1. 4 2. 0 1. 3 3. 1 1. 9

Computing the Median Stem leaf Diagrams Median = middle observation =12 th observation

Summary

Some Comments • The mean is the centre of gravity of a set of observations. The balancing point. • The median splits the observations equally in two parts of approximately 50%

• The median splits the area under a histogram in two parts of 50% • The mean is the balancing point of a histogram 50% median

• For symmetric distributions the mean and the median will be approximately the same value 50% Median &

• For Positively skewed distributions the mean exceeds the median • For Negatively skewed distributions the median exceeds the mean 50% median

• An outlier is a “wild” observation in the data • Outliers occur because – of errors (typographical and computational) – Extreme cases in the population

• The mean is altered to a significant degree by the presence of outliers • Outliers have little effect on the value of the median • This is a reason for using the median in place of the mean as a measure of central location • Alternatively the mean is the best measure of central location when the data is Normally distributed (Bell-shaped)

Measures of Non-Central Location • • Percentiles Quartiles (Hinges, Mid-hinges)

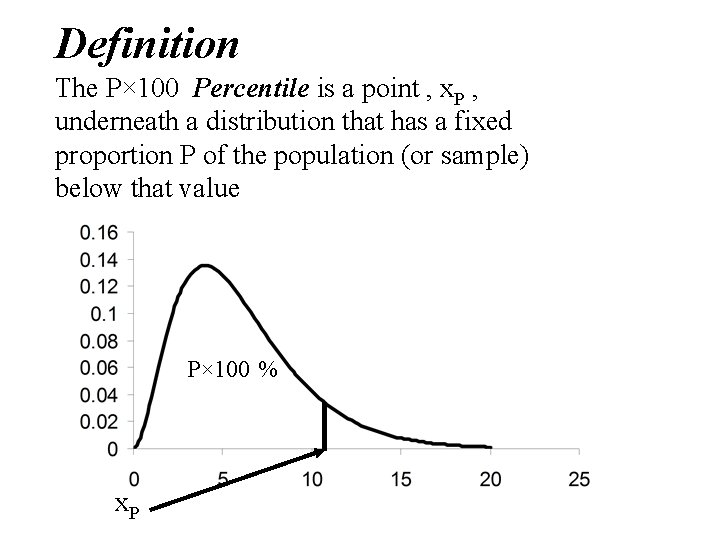
Definition The P× 100 Percentile is a point , x. P , underneath a distribution that has a fixed proportion P of the population (or sample) below that value P× 100 % x. P

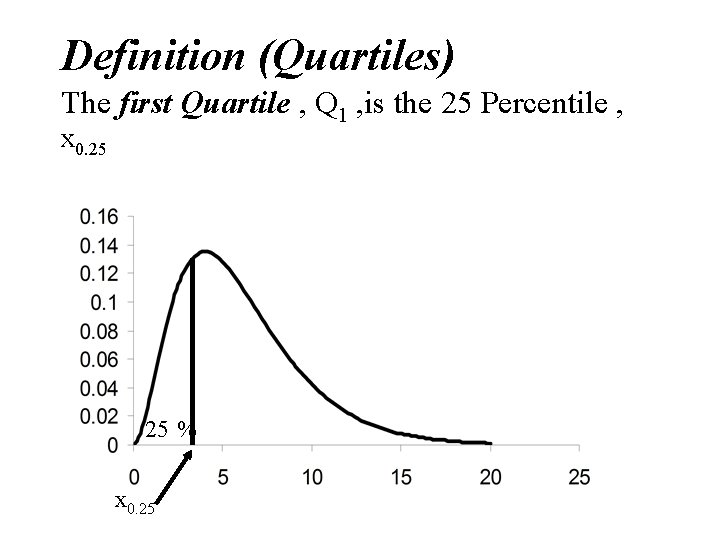
Definition (Quartiles) The first Quartile , Q 1 , is the 25 Percentile , x 0. 25 25 % x 0. 25

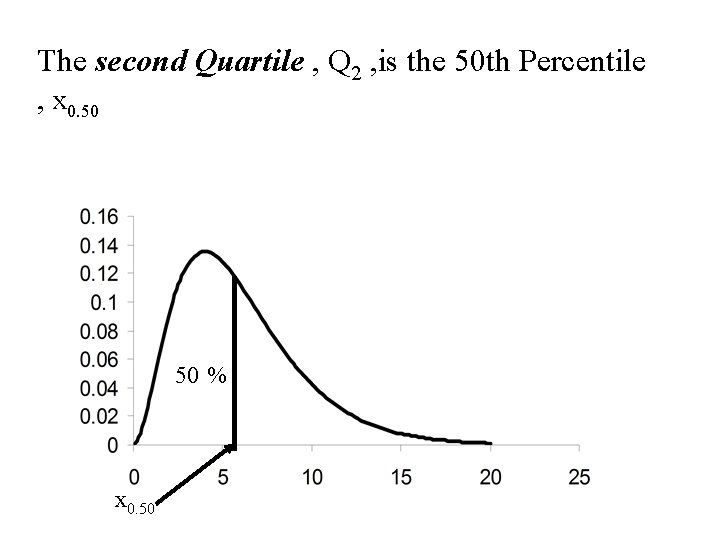
The second Quartile , Q 2 , is the 50 th Percentile , x 0. 50 50 % x 0. 50

• The second Quartile , Q 2 , is also the median and the 50 th percentile

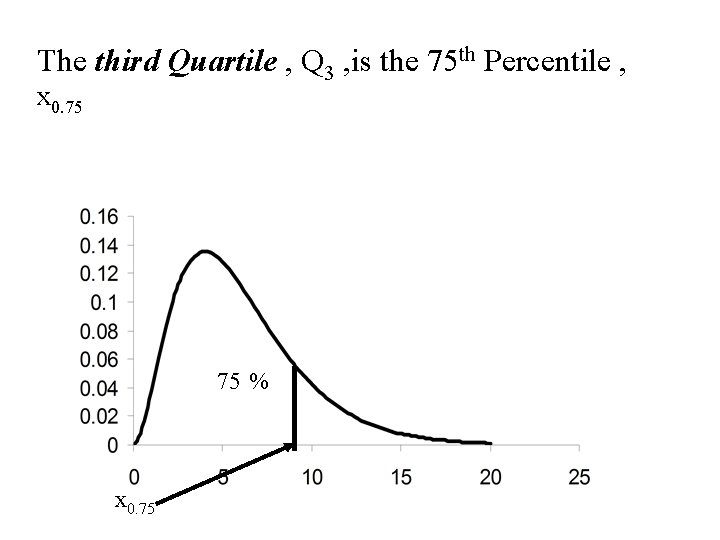
The third Quartile , Q 3 , is the 75 th Percentile , x 0. 75 75 % x 0. 75

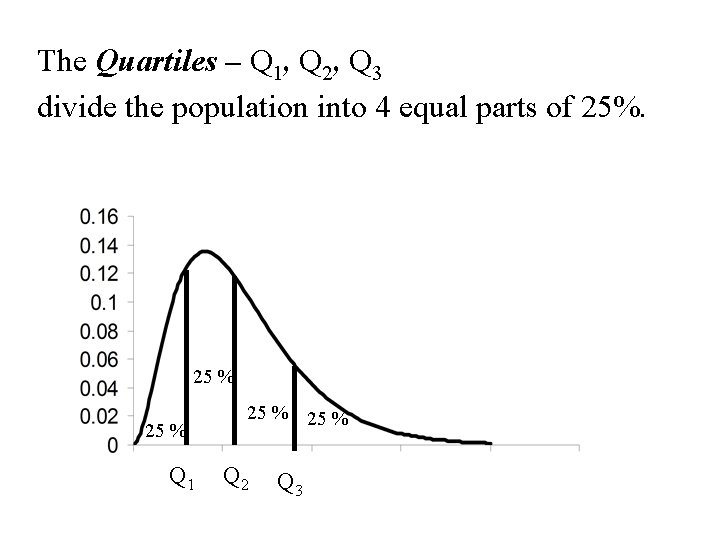
The Quartiles – Q 1, Q 2, Q 3 divide the population into 4 equal parts of 25%. 25 % Q 1 25 % Q 2 Q 3

Computing Percentiles and Quartiles – Method 1 • The first step is to order the observations in increasing order. • We then compute the position, k, of the P× 100 Percentile. k = P × (n+1) Where n = the number of observations

Example The data on n = 23 students Variables • Verbal IQ • Math IQ • Initial Reading Achievement Score • Final Reading Achievement Score We want to compute the 75 th percentile and the 90 th percentile

The position, k, of the 75 th Percentile. k = P × (n+1) =. 75 × (23+1) = 18 The position, k, of the 90 th Percentile. k = P × (n+1) =. 90 × (23+1) = 21. 6 When the position k is an integer the percentile is the kth observation (in order of magnitude) in the data set. For example the 75 th percentile is the 18 th (in size) observation

When the position k is an not an integer but an integer(m) + a fraction(f). i. e. k=m+f then the percentile is x. P = (1 -f) × (mth observation in size) + f × (m+1 st observation in size) In the example the position of the 90 th percentile is: k = 21. 6 Then x. 90 = 0. 4(21 st observation in size) + 0. 6(22 nd observation in size)

When the position k is an not an integer but an integer(m) + a fraction(f). i. e. k=m+f then the percentile is x. P = (1 -f) × (mth observation in size) + f × (m+1 st observation in size) mth obs (m+1)st obs xp = (1 - f) ( mth obs) + f [(m+1)st obs]

When the position k is an not an integer but an integer(m) + a fraction(f). i. e. k = m + f mth obs (m+1)st obs xp = (1 - f) ( mth obs) + f [(m+1)st obs] Thus the position of xp is 100 f% through the interval between the mth observation and the (m +1)st observation

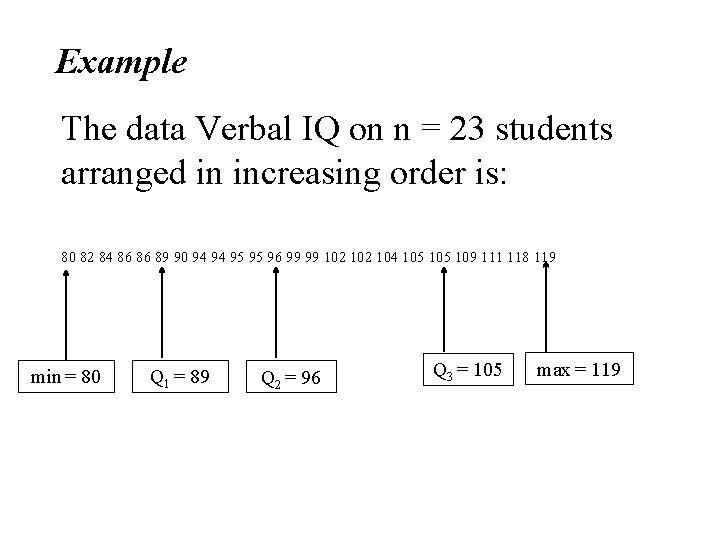
Example The data Verbal IQ on n = 23 students arranged in increasing order is: 80 82 84 86 86 89 90 94 94 95 95 96 99 99 102 104 105 109 111 118 119

x 0. 75 = 75 th percentile = 18 th observation in size =105 (position k = 18) x 0. 90 = 90 th percentile = 0. 4(21 st observation in size) + 0. 6(22 nd observation in size) = 0. 4(111)+ 0. 6(118) = 115. 2 (position k = 21. 6)

An Alternative method for computing Quartiles – Method 2 • Sometimes this method will result in the same values for the quartiles. • Sometimes this method will result in the different values for the quartiles. • For large samples the two methods will result in approximately the same answer.

Let x 1, x 2, x 3, … xn denote a set of n numbers. The first step in Method 2 is to arrange the numbers in increasing order. From the arranged numbers we compute the median. This is also called the Hinge

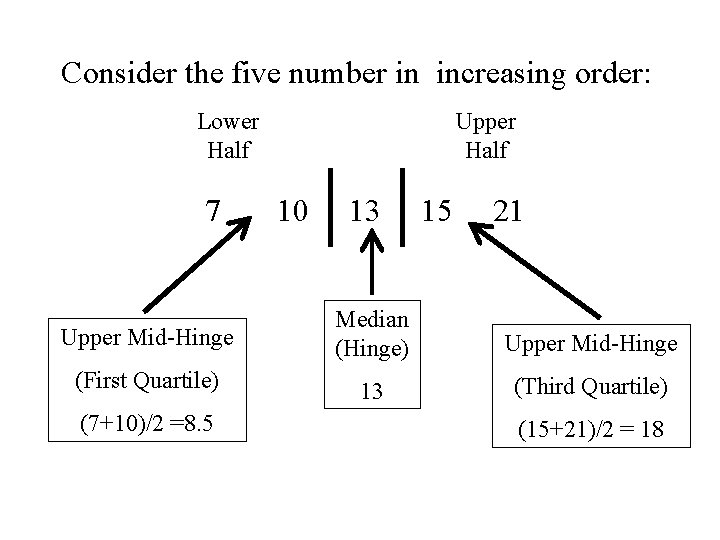
Example Consider the 5 numbers: 10 15 21 7 13 Arranged in increasing order: 7 10 13 15 21 Median (Hinge) The median (or Hinge) splits the observations in half

The lower mid-hinge (the first quartile) is the “median” of the lower half of the observations (excluding the median). The upper mid-hinge (the third quartile) is the “median” of the upper half of the observations (excluding the median).

Consider the five number in increasing order: Lower Half 7 Upper Half 10 13 15 21 Upper Mid-Hinge Median (Hinge) Upper Mid-Hinge (First Quartile) 13 (Third Quartile) (7+10)/2 =8. 5 (15+21)/2 = 18

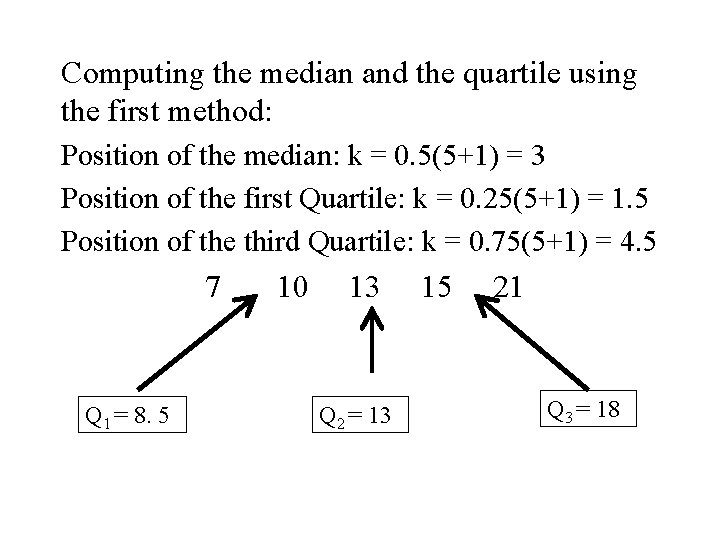
Computing the median and the quartile using the first method: Position of the median: k = 0. 5(5+1) = 3 Position of the first Quartile: k = 0. 25(5+1) = 1. 5 Position of the third Quartile: k = 0. 75(5+1) = 4. 5 7 Q 1 = 8. 5 10 13 Q 2 = 13 15 21 Q 3 = 18

• Both methods result in the same value • This is not always true.

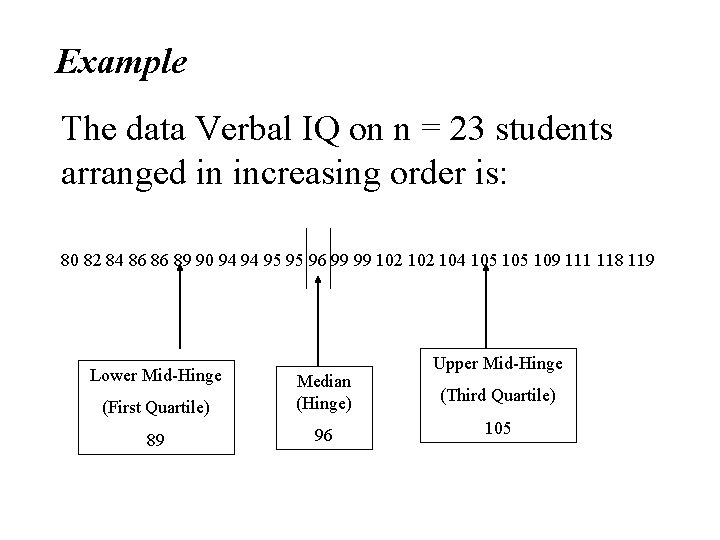
Example The data Verbal IQ on n = 23 students arranged in increasing order is: 80 82 84 86 86 89 90 94 94 95 95 96 99 99 102 104 105 109 111 118 119 Lower Mid-Hinge (First Quartile) Median (Hinge) 89 96 Upper Mid-Hinge (Third Quartile) 105

Computing the median and the quartile using the first method: Position of the median: k = 0. 5(23+1) = 12 Position of the first Quartile: k = 0. 25(23+1) = 6 Position of the third Quartile: k = 0. 75(23+1) = 18 80 82 84 86 86 89 90 94 94 95 95 96 99 99 102 104 105 109 111 118 119 Q 1 = 89 Q 2 = 96 Q 3 = 105

• Many programs compute percentiles, quartiles etc. • Each may use different methods. • It is important to know which method is being used. • The different methods result in answers that are close when the sample size is large.

Measures of Central Location Mean Median
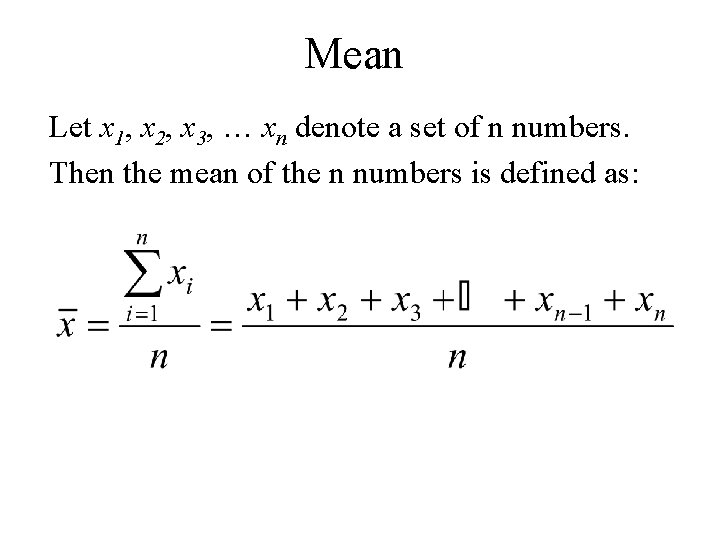
Mean Let x 1, x 2, x 3, … xn denote a set of n numbers. Then the mean of the n numbers is defined as:

The Median Let x 1, x 2, x 3, … xn denote a set of n numbers. Then the median of the n numbers is defined as the number that splits the numbers into two equal parts. To evaluate the median we arrange the numbers in increasing order.

If the number of observations is odd there will be one observation in the middle. This number is the median. If the number of observations is even there will be two middle observations. The median is the average of these two observations

Measures of Non-Central Location • • Percentiles Quartiles (Hinges, Mid-hinges)

Definition The P× 100 Percentile is a point , x. P , underneath a distribution that has a fixed proportion P of the population (or sample) below that value P× 100 % x. P

Computing Percentiles and Quartiles – Method 1 • The first step is to order the observations in increasing order. • We then compute the position, k, of the P× 100 Percentile. k = P × (n+1) Where n = the number of observations

When the position k is an integer the percentile is the kth observation (in order of magnitude) in the data set. When the position k is an not an integer but an integer(m) + a fraction(f). i. e. k = m + f then the percentile is x. P = (1 -f) × (mth observation in size) + f × (m+1 st observation in size)

An Alternative method for computing Quartiles – Method 2 • Sometimes this method will result in the same values for the quartiles. • Sometimes this method will result in the different values for the quartiles. • For large samples the two methods will result in approximately the same answer.

Let x 1, x 2, x 3, … xn denote a set of n numbers. The first step in Method 2 is to arrange the numbers in increasing order. From the arranged numbers we compute the median. This is also called the Hinge

The lower mid-hinge (the first quartile) is the “median” of the lower half of the observations (excluding the median). The upper mid-hinge (the third quartile) is the “median” of the upper half of the observations (excluding the median).

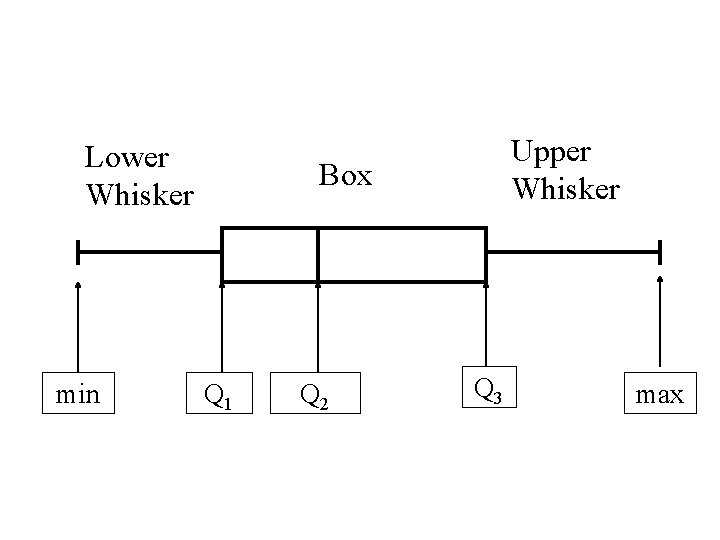
Box-Plots Box-Whisker Plots • A graphical method of of displaying data • An alternative to the histogram and stem-leaf diagram

To Draw a Box Plot • Compute the Hinge (Median, Q 2) and the Mid-hinges (first & third quartiles – Q 1 and Q 3 ) • We also compute the largest and smallest of the observations – the max and the min.

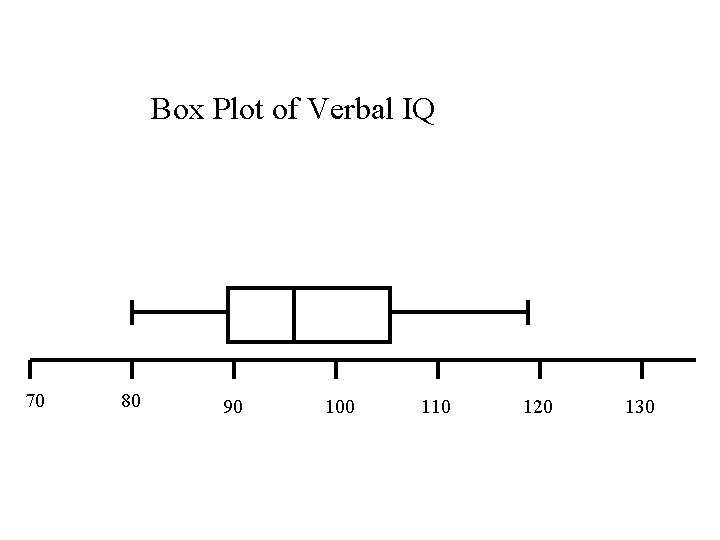
Example The data Verbal IQ on n = 23 students arranged in increasing order is: 80 82 84 86 86 89 90 94 94 95 95 96 99 99 102 104 105 109 111 118 119 min = 80 Q 1 = 89 Q 2 = 96 Q 3 = 105 max = 119

The Box Plot is then drawn • Drawing above an axis a “box” from Q 1 to Q 3. • Drawing vertical line in the box at the median, Q 2 • Drawing whiskers at the lower and upper ends of the box going down to the min and up to max.

Lower Whisker min Upper Whisker Box Q 1 Q 2 Q 3 max

Example The data Verbal IQ on n = 23 students arranged in increasing order is: min = 80 Q 1 = 89 Q 2 = 96 Q 3 = 105 max = 119

Box Plot of Verbal IQ 70 80 90 100 110 120 130

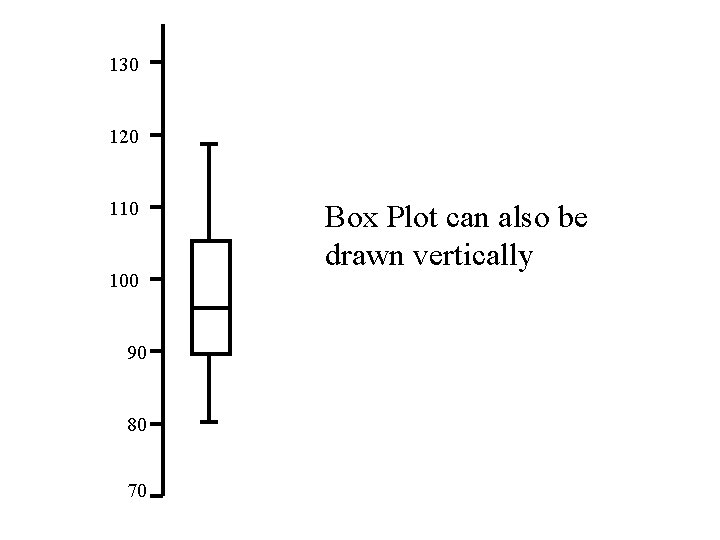
130 120 110 100 90 80 70 Box Plot can also be drawn vertically

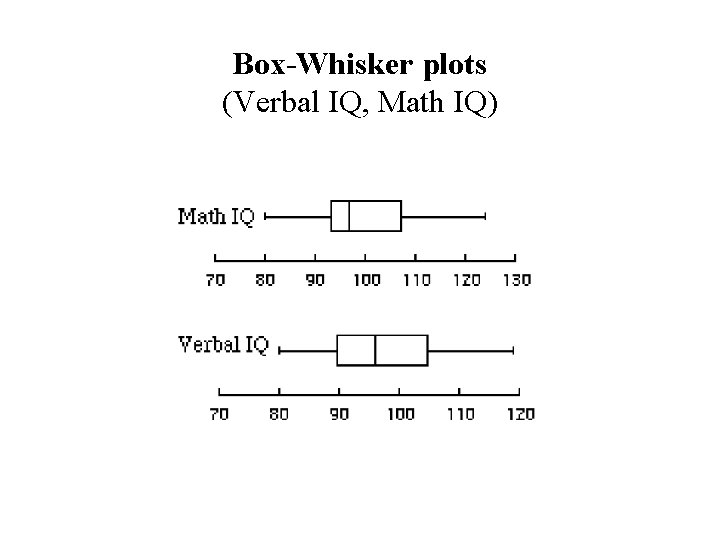
Box-Whisker plots (Verbal IQ, Math IQ)

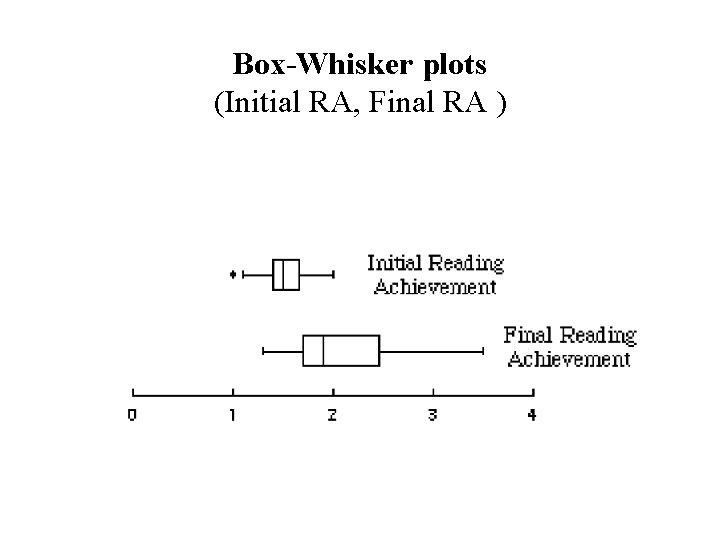
Box-Whisker plots (Initial RA, Final RA )

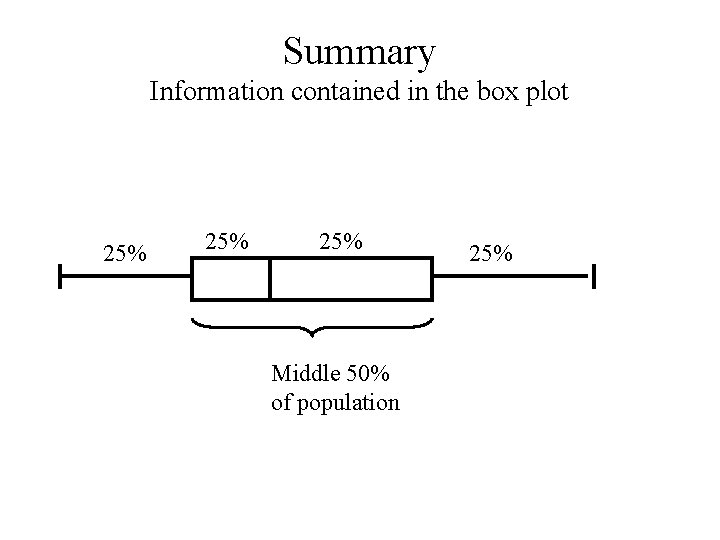
Summary Information contained in the box plot 25% 25% Middle 50% of population 25%

Next topic: Numerical Measures of Variability
 Central tendency symbols
Central tendency symbols Measures of central tendency
Measures of central tendency Measures of central tendency notes
Measures of central tendency notes Choosing the best measure of central tendency worksheets
Choosing the best measure of central tendency worksheets Measures of central tendency range
Measures of central tendency range Statistics chapter 3 measures of central tendency
Statistics chapter 3 measures of central tendency Measures of central tendency and variation
Measures of central tendency and variation Mode for group data
Mode for group data In quartiles central tendency median is
In quartiles central tendency median is Measures of central tendency
Measures of central tendency Measures of central tendency symbols
Measures of central tendency symbols Measures of central tendency for ungrouped data
Measures of central tendency for ungrouped data Unit 6 review #2 - measures of central tendency
Unit 6 review #2 - measures of central tendency Lu 분해 예제
Lu 분해 예제 Mean ka formula
Mean ka formula Central tendency grouped data
Central tendency grouped data Lower boundary of modal class
Lower boundary of modal class Measures of central tendency
Measures of central tendency Central tendency symbols
Central tendency symbols Measure of central tendency and dispersion
Measure of central tendency and dispersion Objective of central tendency
Objective of central tendency Central tendency spss
Central tendency spss Mean median mode example problems
Mean median mode example problems Central tendency symbols
Central tendency symbols Central tendency symbols
Central tendency symbols Variance meaning
Variance meaning Central tendency and spread homework
Central tendency and spread homework Summation notation
Summation notation Contoh soal ukuran tendensi sentral
Contoh soal ukuran tendensi sentral Central tendency
Central tendency Use of central tendency
Use of central tendency Median for odd numbers
Median for odd numbers Ukuran tendensi sentral
Ukuran tendensi sentral Importance of central tendency
Importance of central tendency Objective of central tendency
Objective of central tendency Central tendency
Central tendency How to get frequency distribution
How to get frequency distribution Median
Median Sifat sifat median
Sifat sifat median Central tendancy bias
Central tendancy bias Numerical descriptive measures
Numerical descriptive measures Arithmetic mean for grouped data example
Arithmetic mean for grouped data example Numerical
Numerical Numerical descriptive measures
Numerical descriptive measures Numerical descriptive statistics
Numerical descriptive statistics Numerical summary of data
Numerical summary of data What is the mode for the set of data?
What is the mode for the set of data? Numerical methods of descriptive statistics
Numerical methods of descriptive statistics Numerical descriptive measures exercises
Numerical descriptive measures exercises Numerical descriptive measures
Numerical descriptive measures Repeated measures design vs independent measures design
Repeated measures design vs independent measures design Tendency to be careful scrupulous and persevering
Tendency to be careful scrupulous and persevering Flightscope aviation
Flightscope aviation Selfserving bias
Selfserving bias The actualising tendency
The actualising tendency The perceptual tendency to group together stimuli
The perceptual tendency to group together stimuli The societal tendency toward class stratification
The societal tendency toward class stratification Qg height tendency equation
Qg height tendency equation Projected cognitive similarity is the tendency to
Projected cognitive similarity is the tendency to Bleeding tendency
Bleeding tendency Conformity and compliance
Conformity and compliance The societal tendency toward class stratification
The societal tendency toward class stratification Get2 test
Get2 test Pressure tendency
Pressure tendency Filter blocking tendency
Filter blocking tendency Bleeding tendency
Bleeding tendency Terminal values and instrumental values
Terminal values and instrumental values Buoyancy is a tendency
Buoyancy is a tendency Diffraction is the tendency of light to:
Diffraction is the tendency of light to: Lanthanides have poor tendency to form complexes
Lanthanides have poor tendency to form complexes Numerical geometry of non-rigid shapes
Numerical geometry of non-rigid shapes Numerical identity
Numerical identity Numerical analysis interpolation
Numerical analysis interpolation Numerical
Numerical Numerical
Numerical Numerical coefficient
Numerical coefficient If the compass quadrant bearing is n 790 w, the azimuth is?
If the compass quadrant bearing is n 790 w, the azimuth is? Numerical aperture optical fiber
Numerical aperture optical fiber Numerical differentiation
Numerical differentiation Integration of sec
Integration of sec Snyder radar
Snyder radar Numerical methods for partial differential equations eth
Numerical methods for partial differential equations eth Roger crawfis
Roger crawfis Vicarius filii deis
Vicarius filii deis Cubic hermite interpolation
Cubic hermite interpolation Numerical aperture in microscope
Numerical aperture in microscope What is numerical example
What is numerical example Dark field microscopy
Dark field microscopy Different types of errors in numerical methods
Different types of errors in numerical methods Numerical technologies ltd
Numerical technologies ltd The key vocabulary routine
The key vocabulary routine Numerical derivation
Numerical derivation Interpolation in numerical analysis
Interpolation in numerical analysis C programming and numerical analysis an introduction
C programming and numerical analysis an introduction What is a numerical expression
What is a numerical expression Eigen value problem
Eigen value problem Helmert contrast
Helmert contrast Numerical programming
Numerical programming Jack box
Jack box Numerical descriptive statistics
Numerical descriptive statistics Pros and cons of secant method
Pros and cons of secant method Product of powers
Product of powers Turner syndrome is what numerical chromosome disorder?
Turner syndrome is what numerical chromosome disorder? Numerical geometry of non-rigid shapes
Numerical geometry of non-rigid shapes Psychological continuity
Psychological continuity Taylor series numerical methods
Taylor series numerical methods Simpson's 1/3 rule
Simpson's 1/3 rule Non-numerical unstructured data indexing
Non-numerical unstructured data indexing Specific factors model numerical example
Specific factors model numerical example Numerical patterns
Numerical patterns Numerical variable
Numerical variable Numerical methods
Numerical methods Mathematical preliminaries in numerical computing
Mathematical preliminaries in numerical computing Teeth numbering system
Teeth numbering system Xiaolin wu's line algorithm
Xiaolin wu's line algorithm Erlanger classification
Erlanger classification Representing numerical data
Representing numerical data What are numerical expressions
What are numerical expressions What is numerical aperture
What is numerical aperture Visual numerical learning style
Visual numerical learning style Numerical differentiation examples
Numerical differentiation examples Contoh requirement engineering
Contoh requirement engineering How to calculate percentage
How to calculate percentage What is the value of w in laplace-everett formula
What is the value of w in laplace-everett formula Numerical methods
Numerical methods Relationships between two numerical variables
Relationships between two numerical variables Contoh infix
Contoh infix Numerical stroop
Numerical stroop The banker's algorithm
The banker's algorithm