Numerical Analysis Lecture 42 Examples of Numerical Differentiation








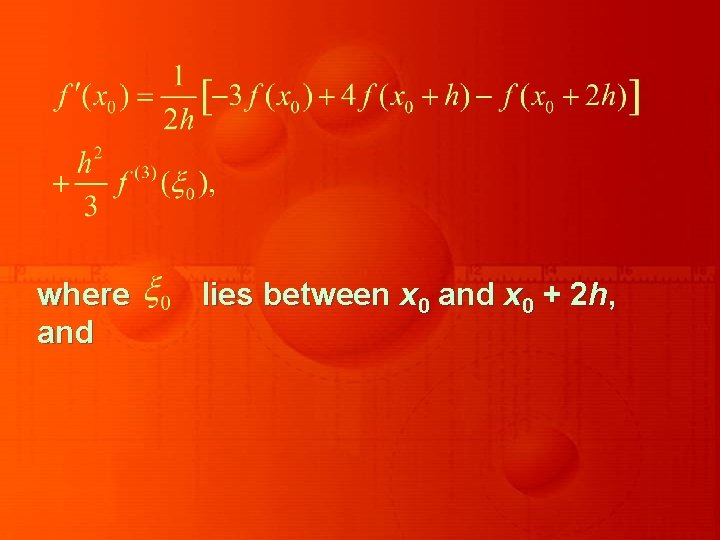




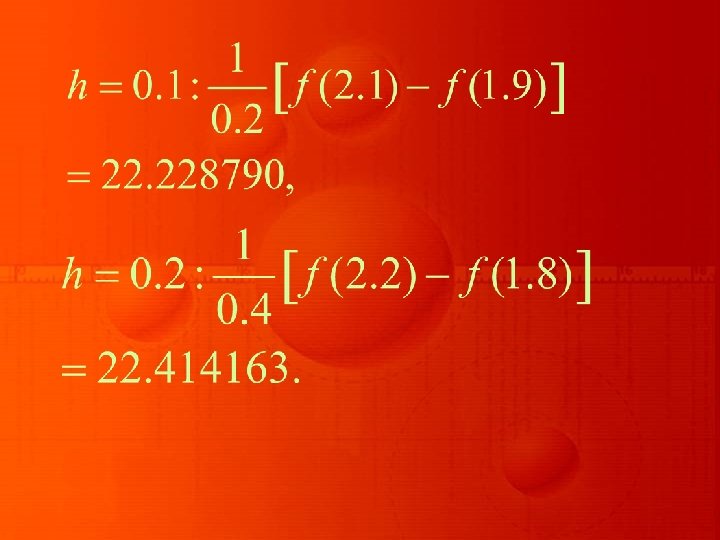




![EXAMPLE The Trapezoidal rule for a function f on the interval [0, 2] is EXAMPLE The Trapezoidal rule for a function f on the interval [0, 2] is](https://slidetodoc.com/presentation_image_h/0e365c2b5c33815b61f399b81bd67a72/image-22.jpg)
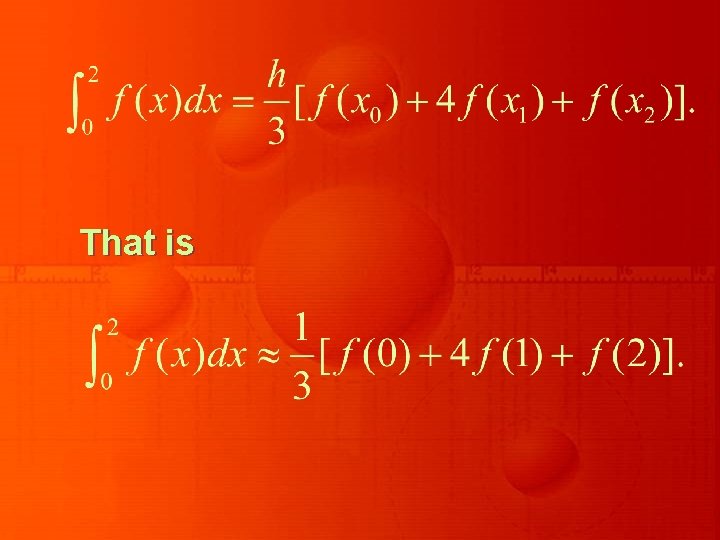


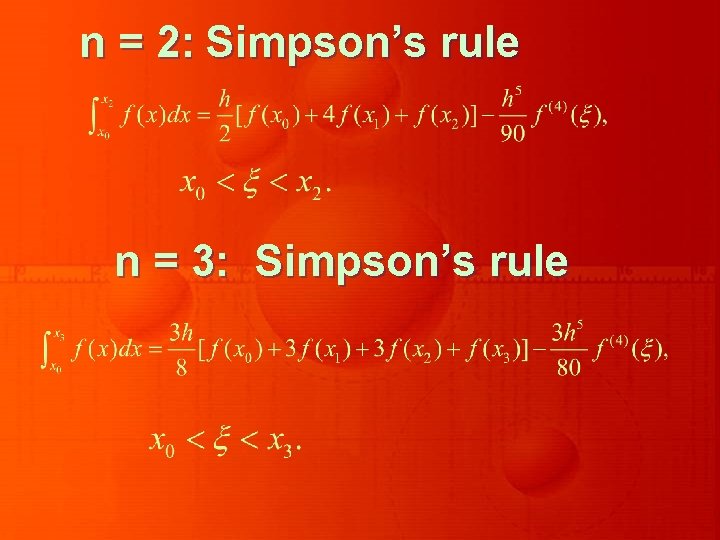




















- Slides: 48

Numerical Analysis Lecture 42

Examples of Numerical Differentiation

The simplest formula for differentiation is

Example Let f(x)= In x and x 0 = 1. 8. Then the quotient is used to approximate

with error where Let us see the results for h = 0. 1, 0. 01, and 0. 001.

h f(1. 8 + h) 0. 1 0. 64185389 0. 5406722 0. 0154321 0. 01 0. 59332685 0. 5540180 0. 0015432 0. 001 0. 58834207 0. 5554013 0. 0001543

Since The exact value of is and the error bounds are a appropriate.

The following two three point formulas become especially useful if the nodes are equally spaced, that is, when x 1 = x 0 + h and x 2 = x 0 + 2 h ,
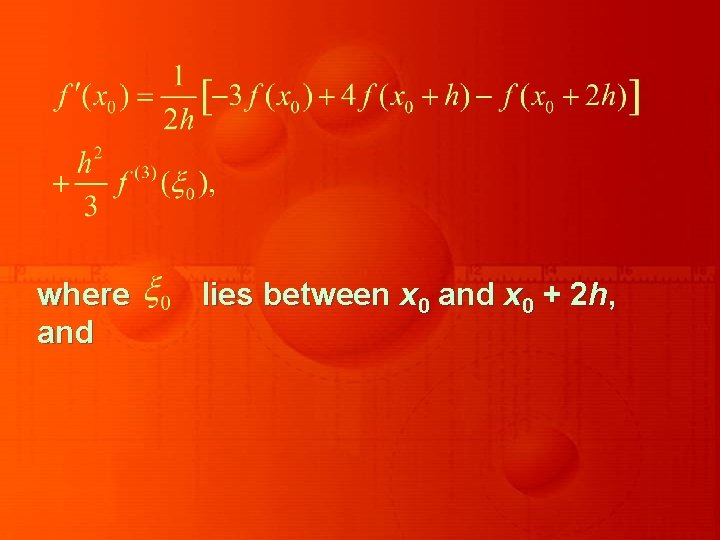
where and lies between x 0 and x 0 + 2 h,

where lies between (x 0 – h) and (x 0 + h).

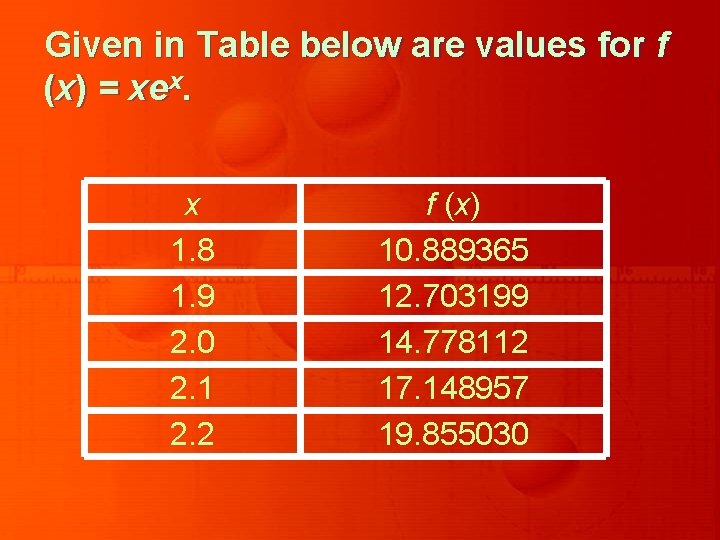
Given in Table below are values for f (x) = xex. x 1. 8 1. 9 2. 0 2. 1 2. 2 f (x) 10. 889365 12. 703199 14. 778112 17. 148957 19. 855030

Since Approximating using the various three-and five-point formulas produces the following results.

Three point formulas:

Using three point formulas we get
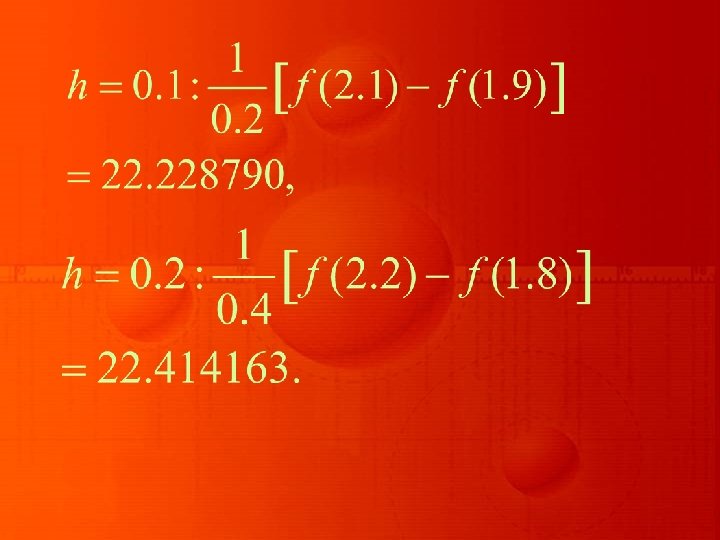

Five point formula Using the five point formula with h = 0. 1 (the only formula applicable):

The errors in the formulas are approximately and respectively. Clearly, the five-point formula gives the superior result.

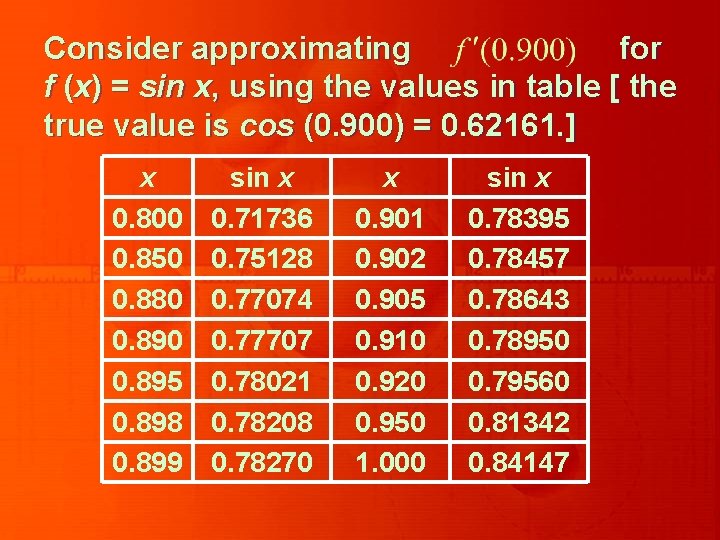
Consider approximating for f (x) = sin x, using the values in table [ the true value is cos (0. 900) = 0. 62161. ] x 0. 800 0. 850 0. 880 0. 895 0. 898 0. 899 sin x 0. 71736 0. 75128 0. 77074 0. 77707 0. 78021 0. 78208 0. 78270 x 0. 901 0. 902 0. 905 0. 910 0. 920 0. 950 1. 000 sin x 0. 78395 0. 78457 0. 78643 0. 78950 0. 79560 0. 81342 0. 84147

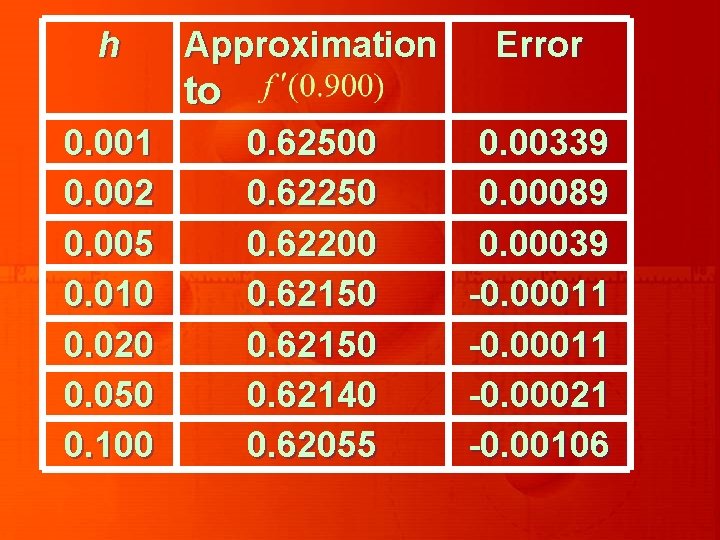
Using the formula with different values of h gives the approximations in table given below:

h Approximation Error to 0. 001 0. 002 0. 005 0. 010 0. 020 0. 050 0. 100 0. 62500 0. 62250 0. 62200 0. 62150 0. 62140 0. 62055 0. 00339 0. 00089 0. 00039 -0. 00011 -0. 00021 -0. 00106

Examples of Numerical Integration
![EXAMPLE The Trapezoidal rule for a function f on the interval 0 2 is EXAMPLE The Trapezoidal rule for a function f on the interval [0, 2] is](https://slidetodoc.com/presentation_image_h/0e365c2b5c33815b61f399b81bd67a72/image-22.jpg)
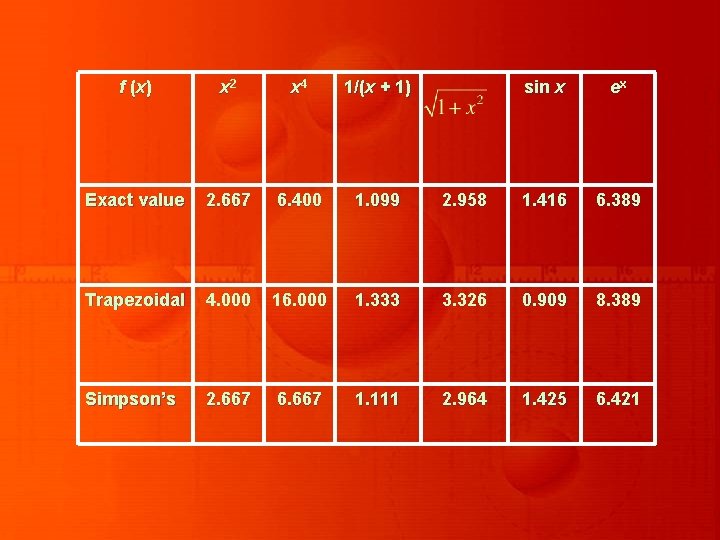
EXAMPLE The Trapezoidal rule for a function f on the interval [0, 2] is while Simpson’s rule for f on [0, 2] is
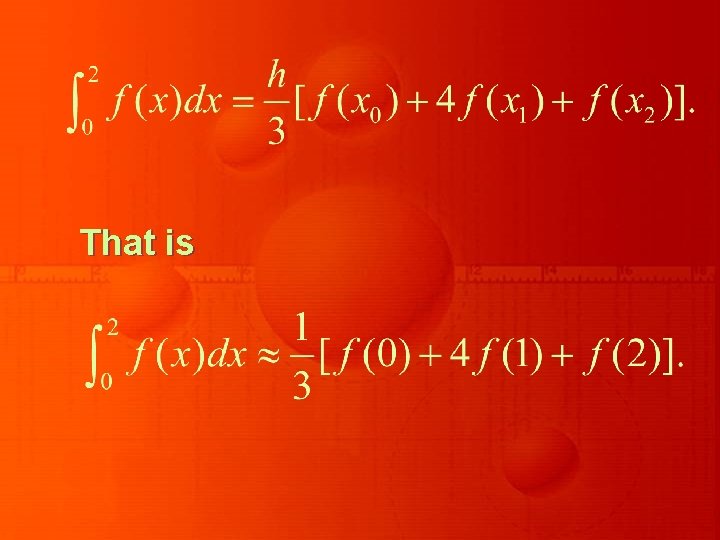
That is

f ( x) x 2 x 4 1/(x + 1) sin x ex Exact value 2. 667 6. 400 1. 099 2. 958 1. 416 6. 389 Trapezoidal 4. 000 16. 000 1. 333 3. 326 0. 909 8. 389 Simpson’s 2. 667 6. 667 1. 111 2. 964 1. 425 6. 421

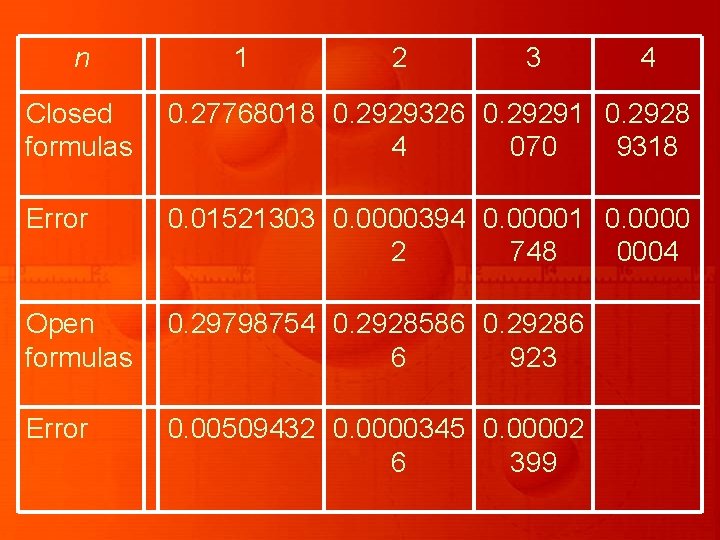
Use close and open formulas listed below to approximate

Some of the common closed Newton-Cotes formulas with their error terms are as follows: n = 1: where Trapezoidal rule
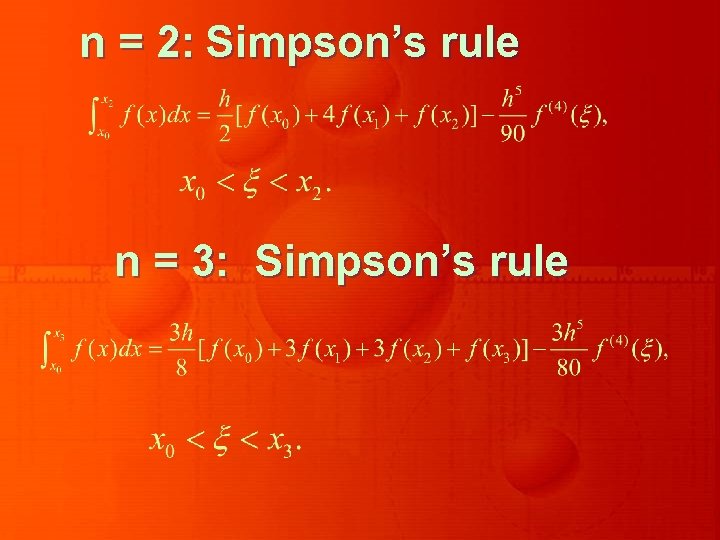
n = 2: Simpson’s rule n = 3: Simpson’s rule

n = 4: where n = 0: Midpoint rule where

n 1 2 3 4 Closed formulas 0. 27768018 0. 2929326 0. 29291 0. 2928 4 070 9318 Error 0. 01521303 0. 0000394 0. 00001 0. 0000 2 748 0004 Open formulas 0. 29798754 0. 2928586 0. 29286 6 923 Error 0. 00509432 0. 0000345 0. 00002 6 399

Composite Numerical Integration EXAMPLE 1 Consider approximating with an absolute error less than 0. 00002, using the Composite Simpson’s rule. The Composite Simpson’s rule gives

Since the absolute error is required to be less than 0. 00002, the inequality

is used to determine n and h. Computing these calculations gives n greater than or equal to 18. If n = 20, then the formula becomes

To be assured of this degree of accuracy using the Composite Trapezoidal rule requires that or that Since this is many more calculations than are needed for the Composite Simpson’s rule, it is clear that it

would be undesirable to use the Composite Trapezoidal rule on this problem. For comparison purposes, the Composite Trapezoidal rule with n = 20 and gives

The exact answer is 2; so Simpson’s rule with n = 20 gave an answer well within the required error bound, whereas the Trapezoidal rule with n = 20 clearly did not.

An Example of Industrial applications: A company advertises that every roll of toilet paper has at least 250 sheets. The probability that there are 250 or more sheets in the toilet paper is given by

Approximating the above integral as a)use single segment Trapezoidal rule to find the probability that there are 250 or more sheets. b)Find the true error, Et for part (a). C)Find the absolute relative true error for part (a).

, where

b) The exact value of the above integral cannot be found. We assume the value obtained by adaptive numerical integration using Maple as the exact value for calculating the true error and relative true error. so the true error is

The absolute relative true error, , would then be

Improper Integrals EXAMPLE To approximate the values of the improper integral we will use the Composite Simpson’s rule with h = 0. 25. Since the fourth Taylor polynomial for ex about x = 0 is

We have

Table below lists the approximate values of x 0. 00 0. 25 0. 50 0. 75 1. 00 G(x) 0 0. 0000170 0. 0004013 0. 0026026 0. 0099485

Applying the Composite Simpson’s rule to G using these data gives Hence

This result is accurate within the accuracy of the Composite Simpson’s rule approximation for the function G. Since on [0, 1], the error is bounded by

EXAMPLE To approximate the value of the improper integral we make the change of variable t = x-1 to obtain The fourth Taylor polynomial, P 4(t), for sin t about 0 is

So we have Applying the Composite Simpson’s rule with n = 8 to the remaining integral gives which is accurate to within

Numerical Analysis Lecture 42
 Numerical differentiation examples
Numerical differentiation examples Numerical derivation
Numerical derivation Central derivative formula
Central derivative formula Roger crawfis
Roger crawfis Numerical differentiation
Numerical differentiation Newton backward interpolation formula
Newton backward interpolation formula 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Graphical method numerical analysis
Graphical method numerical analysis (x+1)^3 formula
(x+1)^3 formula Numerical analysis formula
Numerical analysis formula Interpolation
Interpolation Different types of errors in numerical methods
Different types of errors in numerical methods Secant method calculator
Secant method calculator C programming and numerical analysis an introduction
C programming and numerical analysis an introduction Weddle's rule in numerical analysis
Weddle's rule in numerical analysis Numerical analysis
Numerical analysis Professional goals ttess
Professional goals ttess Partial differential equation
Partial differential equation Differentiation product rule
Differentiation product rule Find y
Find y Exploratory data analysis lecture notes
Exploratory data analysis lecture notes Sensitivity analysis lecture notes
Sensitivity analysis lecture notes Factor analysis lecture notes
Factor analysis lecture notes Analysis of algorithms lecture notes
Analysis of algorithms lecture notes Streak plate method
Streak plate method Zline 667-36
Zline 667-36 Numerical expression examples
Numerical expression examples What are secondary keywords
What are secondary keywords Numerical expression
Numerical expression Sifat dari variabel kategorik
Sifat dari variabel kategorik Wida language objectives
Wida language objectives Difference between udl and differentiation
Difference between udl and differentiation High accuracy differentiation formulas
High accuracy differentiation formulas Derivatives of algebraic functions
Derivatives of algebraic functions Porter's generic strategies
Porter's generic strategies Social differentiation definition
Social differentiation definition Velocity function
Velocity function Derivative implicit
Derivative implicit Derivative 1/x
Derivative 1/x Delayed differentiation and modular design
Delayed differentiation and modular design Orthogonal unit differentiation
Orthogonal unit differentiation Reciprocal rule differentiation
Reciprocal rule differentiation Carpet patch differentiation
Carpet patch differentiation Science differentiation in action
Science differentiation in action Differentiation of tan inverse x
Differentiation of tan inverse x Diff of sec^2x
Diff of sec^2x Differentiation formulas
Differentiation formulas Despair vs integrity
Despair vs integrity How differentiation works
How differentiation works