Numerical geometry of nonrigid shapes In the Rigid

Numerical geometry of non-rigid shapes In the Rigid Kingdom 1 . . . He had Cinderella sit down, and, putting the slipper to her foot, he found that it went on very easily, fitting her as if it had been made of wax. C. Perrault, Cinderella In the Rigid Kingdom Alexander Bronstein, Michael Bronstein © 2008 All rights reserved. Web: tosca. cs. technion. ac. il

Imagine a glamorous ball… Numerical geometry of non-rigid shapes In the Rigid Kingdom 2

A fairy tale shape similarity problem Numerical geometry of non-rigid shapes In the Rigid Kingdom 3

4 Numerical geometry of non-rigid shapes In the Rigid Kingdom Extrinsic shape similarity n Given two shapes and n Compare as subsets of the Euclidean space and , find the degree of their incongruence. . n Invariance to rigid motion: rotation, translation, (reflection): n is a rotation matrix, n is a translation vector

5 Numerical geometry of non-rigid shapes In the Rigid Kingdom How to get rid of Euclidean isometries? n How to remove translation and rotation ambiguity? n Find some “canonical” placement of the shape in . n Extrinsic centroid (a. k. a. center of mass, or center of gravity): n Set to resolve translation ambiguity. n Three degrees of freedom remaining…

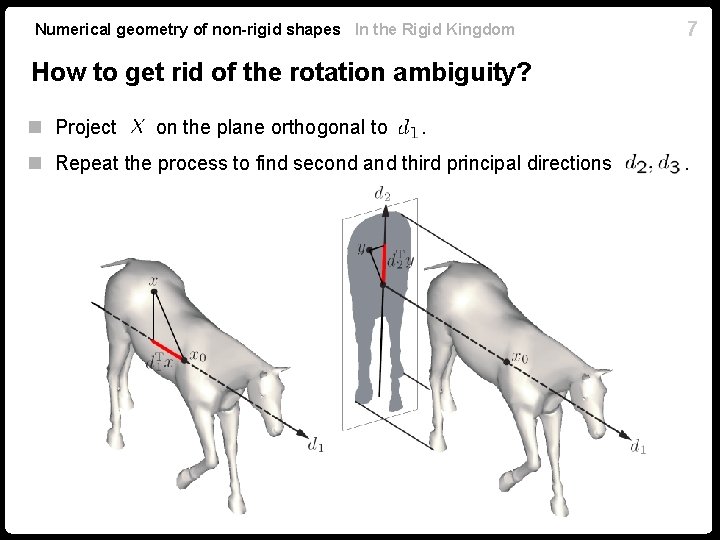
Numerical geometry of non-rigid shapes In the Rigid Kingdom How to get rid of the rotation ambiguity? n Find the direction in which the surface has maximum extent. n Maximize variance of projection of n onto is the covariance matrix n Second-order geometric moments of n is the first principal direction : 6

Numerical geometry of non-rigid shapes In the Rigid Kingdom 7 How to get rid of the rotation ambiguity? n Project on the plane orthogonal to . n Repeat the process to find second and third principal directions .

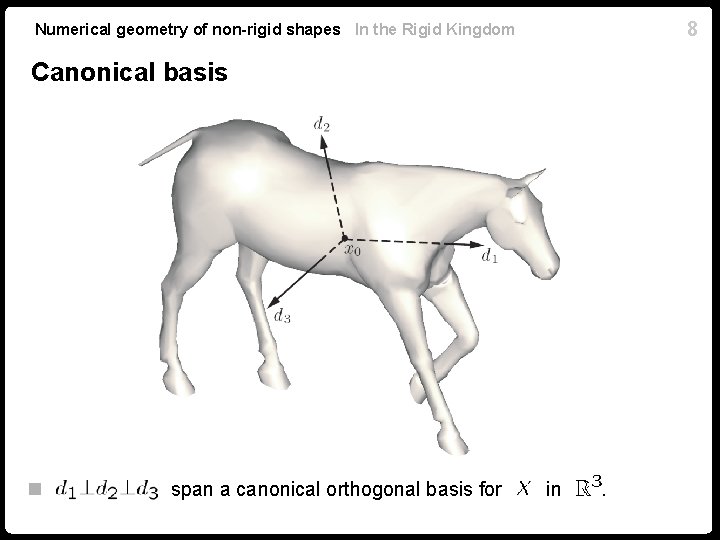
8 Numerical geometry of non-rigid shapes In the Rigid Kingdom Canonical basis n span a canonical orthogonal basis for in .

9 Numerical geometry of non-rigid shapes In the Rigid Kingdom How to get rid of the rotation ambiguity? n Direction maximizing n and n = largest eigenvector of correspond to the second and third eigenvectors of admits unitary diagonalization n Setting axes . aligns . with the standard basis . n Principal component analysis (PCA), a. k. a. Karhunen-Loéve transform (KLT), or Hotelling transform. n Bottom line: the transformation brings the shape into a canonical configuration in . .

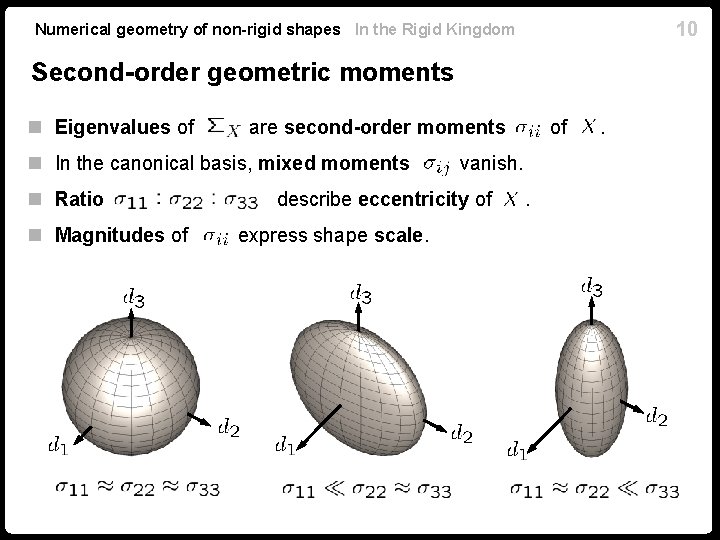
10 Numerical geometry of non-rigid shapes In the Rigid Kingdom Second-order geometric moments n Eigenvalues of are second-order moments n In the canonical basis, mixed moments n Ratio n Magnitudes of vanish. describe eccentricity of express shape scale. of. .

Numerical geometry of non-rigid shapes In the Rigid Kingdom Higher-order geometric moments n Second-order moments allow some discrimination. n Use higher-order moments gives more discrimination. n -th order moment n Computed in the canonical basis. n Invariant to rigid motion. n Signature of moments n A fingerprint of the extrinsic geometry of . 11

12 Numerical geometry of non-rigid shapes In the Rigid Kingdom A signal decomposition intuition n Moments are decomposition coefficients in the monomial basis n is a Dirac delta function elsewhere. n span . for and

Numerical geometry of non-rigid shapes In the Rigid Kingdom 13 A signal decomposition intuition n uniquely identify a shape (up to a rigid motion). can be reconstructed exactly from is the bi-orthonormal basis, i. e. n The monomial basis is not orthogonal. n The bi-orthonormal basis is ugly, but we do not need to reconstruct .

14 Numerical geometry of non-rigid shapes In the Rigid Kingdom Truncated signatures of moments n Compute the truncated moment signature n Construct a moments distance function, e. g. n A distance function on the shape of spaces. n Quantifies the extrinsic dissimilarity of and .

15 Numerical geometry of non-rigid shapes In the Rigid Kingdom Moments distance n is small for nearly congruent n is large for strongly non-congruent n If and are truly congruent, n However, congruent (unless does not imply that . and are ). n Which shapes are indistinguishable by ? n Ideally, congruent at a coarse resolution (“low frequency”) and differing in fine details (“high frequency”). n Degree of coarseness is controlled by the moments order n Geometric moments do not satisfy this requirement. .

Numerical geometry of non-rigid shapes In the Rigid Kingdom Other moments n Instead of the monomial basis, other bases can be chosen n Fourier basis n Spherical harmonics, Zernike polynomials, wavelets, etc. 16

Numerical geometry of non-rigid shapes In the Rigid Kingdom 17 Moments of joy, moments of sorrow Joy: n Shape similarity is translated to similarity of moment signatures. n Comparison of moments signatures is fast (e. g. Euclidean distance). Sorrow: n Do not allow for partial similarity!

18 Numerical geometry of non-rigid shapes In the Rigid Kingdom Iterative closest point (ICP) algorithms n Given two shapes bringing n and , find the best rigid motion as close as possible to : is some shape-to-shape distance. n Minimum = extrinsic dissimilarity of and n Minimizer = best rigid alignment between . and . n ICP is a family of algorithms differing in n The choice of the shape-to-shape distance. n The choice of the numerical minimization algorithm.

19 Numerical geometry of non-rigid shapes In the Rigid Kingdom Shape-to-shape distance n The Hausdorff distance n the shape and is the distance between a point and . n the shape is the distance between a point .

Numerical geometry of non-rigid shapes In the Rigid Kingdom Shape-to-shape distance n A non-symmetric version is preferred to allow for partial similarity n The n Use the n (max-min) formulation is sensitive to outliers. variant is a point-to-shape distance. n Different possibilities to define . 20

21 Numerical geometry of non-rigid shapes In the Rigid Kingdom Point-to-point distance n Treat as a cloud of points. n Find the closest point n Define the distance as to on .

Numerical geometry of non-rigid shapes In the Rigid Kingdom Point-to-plane distance n Treat n as a plane, and define the point-to-plane distance is the normal to the surface at point n Can be approximated as . 22

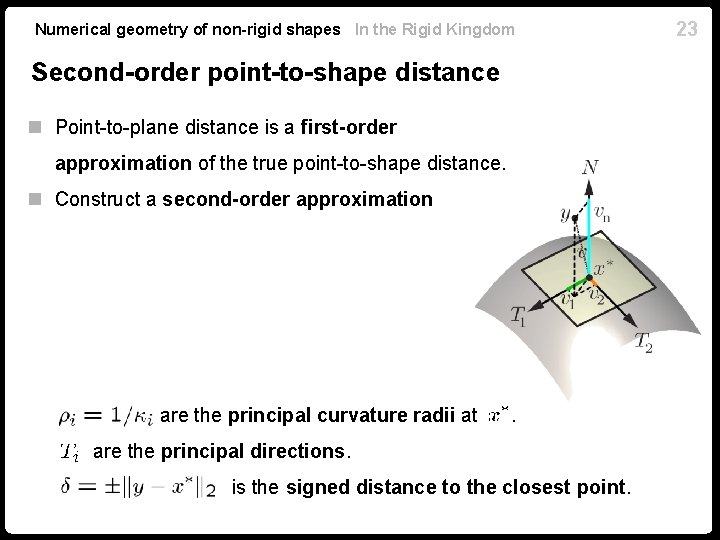
Numerical geometry of non-rigid shapes In the Rigid Kingdom Second-order point-to-shape distance n Point-to-plane distance is a first-order approximation of the true point-to-shape distance. n Construct a second-order approximation are the principal curvature radii at . are the principal directions. is the signed distance to the closest point. 23

Numerical geometry of non-rigid shapes In the Rigid Kingdom Second-order point-to-shape distance n The second-order distance approximant may become negative for some values of . n Use a non-negative quadratic approximant 24

Numerical geometry of non-rigid shapes In the Rigid Kingdom Second-order point-to-shape distance n “Near-field” case – point-to-plane distance n “Far-field” case – point-to-point distance 25

Numerical geometry of non-rigid shapes In the Rigid Kingdom 26 Second-order point-to-shape distance n Second-order distance generalizes the point-to-point and the point-toplane distances. n Gives more accurate alignment between shapes. n Requires principal curvatures and directions (second-order quantities).

Numerical geometry of non-rigid shapes In the Rigid Kingdom Iterative closest point algorithm n Initialize n Find the closest point correspondence n Minimize the misalignment between corresponding points n Update n Iterate until convergence… 27

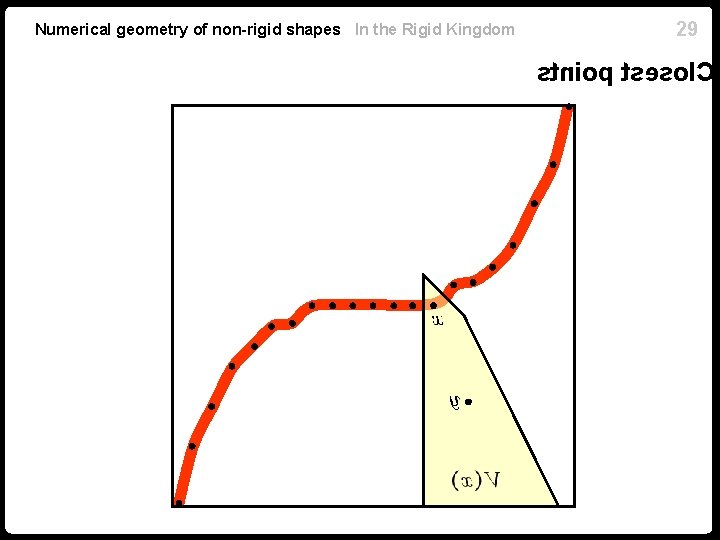
28 Numerical geometry of non-rigid shapes In the Rigid Kingdom Closest points n How to find closest points efficiently? n Straightforward complexity: number of points on n , number of points on . divides the space into Voronoi cells n Given a query point , determine to which cell it belongs.

Numerical geometry of non-rigid shapes In the Rigid Kingdom 29 stniop tsesol. C

30 Numerical geometry of non-rigid shapes In the Rigid Kingdom Approximate nearest neighbors n To reduce search complexity, approximate Voronoi cells. n Use binary space partition trees (e. g. kd-trees or octrees). n Approximate nearest neighbor search complexity: .

Numerical geometry of non-rigid shapes In the Rigid Kingdom Best alignment n Given two sets and of corresponding points. n Find best alignment n A numerical minimization algorithm can be used. n For some point-to-shape distances, a closed-form solution exists. 31

Numerical geometry of non-rigid shapes In the Rigid Kingdom ® MATLAB intermezzo Iterative closest point algorithm 32

33 Numerical geometry of non-rigid shapes In the Rigid Kingdom Until convergence… n ICP should find the solution of n Instead, it solves n Correspondence fixed to instead of . n Not guaranteed to produce a monotonically decreasing sequence of values of . n Not guaranteed to converge!

Numerical geometry of non-rigid shapes In the Rigid Kingdom Enter numerical optimization n Treat as a numerical minimization problem. n Express the distance terms as a quadratic function is a 3× 3 symmetric positive definite matrix, is 3× 1 vector, and is a scalar. 34

Numerical geometry of non-rigid shapes In the Rigid Kingdom Local quadratic approximant n Point-to-point distance: n Point-to-plane distance: 35

Numerical geometry of non-rigid shapes In the Rigid Kingdom Local quadratic approximant n Minimize over . n Dependence of n For small motion and on might be complicated. , hence 36

Numerical geometry of non-rigid shapes In the Rigid Kingdom Minimization variables n is required to be unitary (orthonormal). n Enforcing orthonormality is cumbersome. n Minimization w. r. t. to the rotation angles involves nonlinear functions. n Under small motion assumption, n Linearize rotation matrix 37

38 Numerical geometry of non-rigid shapes In the Rigid Kingdom Let Newton be! n Linearized rotation yields a quadratic objective w. r. t n Use a Newton step to find the steepest descent direction. n Approximation is valid only for small steps. n Use Armijo rule to find a fractional step ensuring sufficient decrease of objective function. n What is a fractional step? .

39 Numerical geometry of non-rigid shapes In the Rigid Kingdom Fractional step n Let n n Hence be a small transformation, which applied is a rotation by . times gives .

Numerical geometry of non-rigid shapes In the Rigid Kingdom Iterative closest point algorithm revisited n Initialize n Find closest point correspondence n Construct local quadratic approximant of n Find Newton direction n Use Armijo rule to find such that n Update n Iterate until convergence… 40

41 Numerical geometry of non-rigid shapes In the Rigid Kingdom Iterative closest point algorithm revisited n Coefficients of the quadratic approximant can be computed on demand using efficient nearest neighbor search. n Alternative: approximate the values of using a space partition tree. in the space

Numerical geometry of non-rigid shapes In the Rigid Kingdom 42 Summary and suggested reading n Rigid shape similarity R. C. Veltkamp and M. Hagedoorn, Shape similarity measures, properties, and constructions, (2001). n Moment-based shape descriptors R. J. Prokop and A. P. Reeves, A survey of moment-based techniques for unoccluded object representation and recognition, Graphical Models and Image Processing 54 (1992), no. 5, 438– 460. D. Zhang and G. Lu, Review of shape representation and description techniques, Pattern Recognition 37 (2004), 1– 19. n Signal decomposition and reconstruction insights M. Elad, P. Milanfar, and G. H. Golub, Shape from moments-an estimation theory perspective, IEEE Trans. Signal Processing 52 (2004), no. 7, 1814– 1829. n Partial shape similarity More on partial similarity in upcoming lectures…

Numerical geometry of non-rigid shapes In the Rigid Kingdom 43 Summary and suggested reading n Iterative closest point algorithms S. Rusinkiewicz and M. Levoy, Efficient variants of the ICP algorithm, Proc. 3 D Digital Imaging and Modeling (2001), 145– 152. n Point-to-shape distances: point-to-point, point-to-plane, second-order. n Fast and approximate nearest neighbor search S. Arya and D. M. Mount, Approximate nearest neighbor searching, Proc. 4 th ACM-SIAM Symposium on Discrete Algorithms (1993), 271– 280. n Convergence of ICP E. Ezra, M. Sharir, and A. Efrat, On the ICP algorithm, Proc. Symp. Computational Geometry (2006), 95– 104. D. Arthur and S. Vassilvitskii, Worst-case and smoothed analysis of the ICP algorithm, with an application to the k-means method, Proc. Symp. Foundations of Computer Science (2006), 153– 164.

Numerical geometry of non-rigid shapes In the Rigid Kingdom 44 Summary and suggested reading n ICP from the point of view of numerical optimization N. J. Mitra, N. Gelfand, H. Pottmann, and L. Guibas, Registration of point cloud data from a geometric optimization perspective, Proc. Symp. Geometry Processing (SGP), 2004, pp. 23– 32. n ICP initialization and global optimality N. Gelfand, N. J. Mitra, L. Guibas, and H. Pottmann, Robust global registration, Proc. Symp. Geometry Processing (SGP) (2005). H. Li and R. Hartley, The 3 D-3 D registration problem revisited, Proc. ICCV, 2007.