Numerical geometry of nonrigid shapes Numerical optimization 1

Numerical geometry of non-rigid shapes Numerical optimization 1 Numerical optimization © Alexander & Michael Bronstein, 2006 -2009 © Michael Bronstein, 2010 tosca. cs. technion. ac. il/book 048921 Advanced topics in vision Processing and Analysis of Geometric Shapes EE Technion, Spring 2010

Numerical geometry of non-rigid shapes Numerical optimization Slowest Longest Shortest Maximal Fastest Minimal Largest Smallest Common denominator: optimization problems 2

Numerical geometry of non-rigid shapes Numerical optimization Optimization problems Generic unconstrained minimization problem where n Vector space n is the search space is a cost (or objective) function n A solution n The value is the minimizer of is the minimum 3

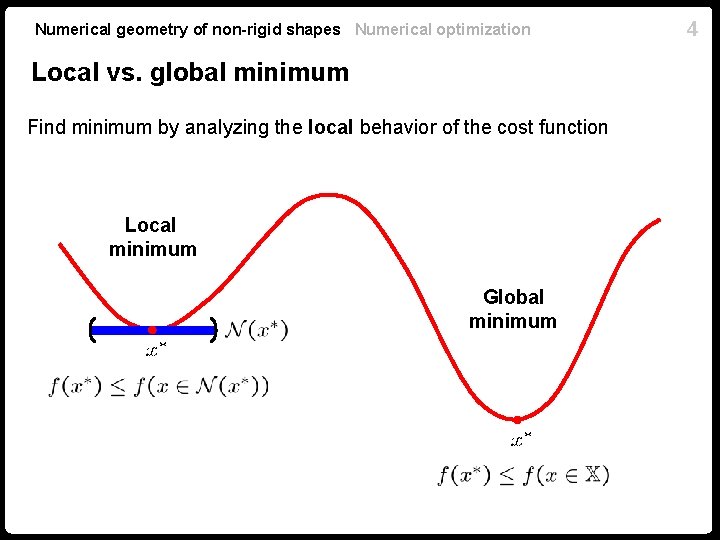
Numerical geometry of non-rigid shapes Numerical optimization Local vs. global minimum Find minimum by analyzing the local behavior of the cost function Local minimum Global minimum 4

Numerical geometry of non-rigid shapes Numerical optimization Local vs. global in real life False summit 8, 030 m Main summit 8, 047 m Broad Peak (K 3), 12 th highest mountain on Earth 5

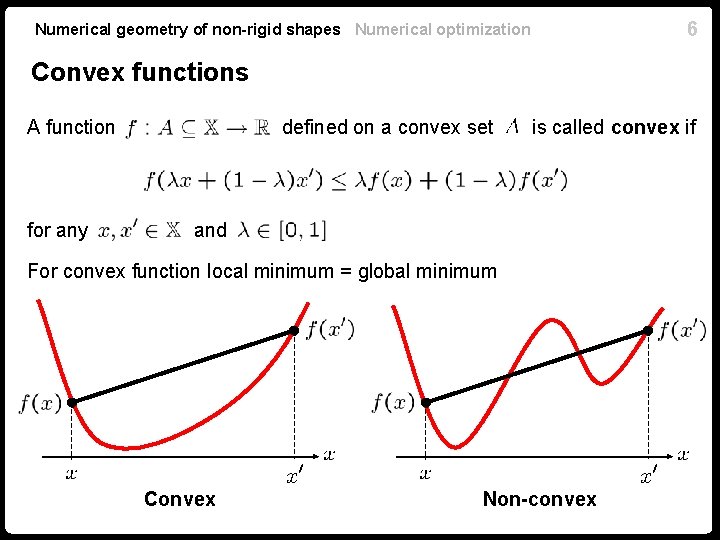
6 Numerical geometry of non-rigid shapes Numerical optimization Convex functions A function for any defined on a convex set is called convex if and For convex function local minimum = global minimum Convex Non-convex

7 Numerical geometry of non-rigid shapes Numerical optimization One-dimensional optimality conditions Point n is the local minimizer of a -function if . n Approximate a function around as a parabola using Taylor expansion guarantees the minimum at guarantees the parabola is convex

Numerical geometry of non-rigid shapes Numerical optimization Gradient In multidimensional case, linearization of the function according to Taylor gives a multidimensional analogy of the derivative. The function , denoted as , is called the gradient of In one-dimensional case, it reduces to standard definition of derivative 8

9 Numerical geometry of non-rigid shapes Numerical optimization Gradient In Euclidean space ( ), can be represented in standard basis in the following way: i-th place which gives

10 Numerical geometry of non-rigid shapes Numerical optimization Example 1: gradient of a matrix function Given (space of real matrices) with standard inner product Compute the gradient of the function an matrix For square matrices where is

11 Numerical geometry of non-rigid shapes Numerical optimization Example 2: gradient of a matrix function Compute the gradient of the function an matrix where is

Numerical geometry of non-rigid shapes Numerical optimization 12 Hessian Linearization of the gradient gives a multidimensional analogy of the secondorder derivative. The function is called the Hessian of , denoted as Ludwig Otto Hesse (1811 -1874) In the standard basis, Hessian is a symmetric matrix of mixed second-order derivatives

13 Numerical geometry of non-rigid shapes Numerical optimization Optimality conditions, bis Point n is the local minimizer of a -function if . n for all matrix (denoted , i. e. , the Hessian is a positive definite ) Approximate a function around as a parabola using Taylor expansion guarantees the minimum at guarantees the parabola is convex

Numerical geometry of non-rigid shapes Numerical optimization Optimization algorithms Descent direction Step size 14

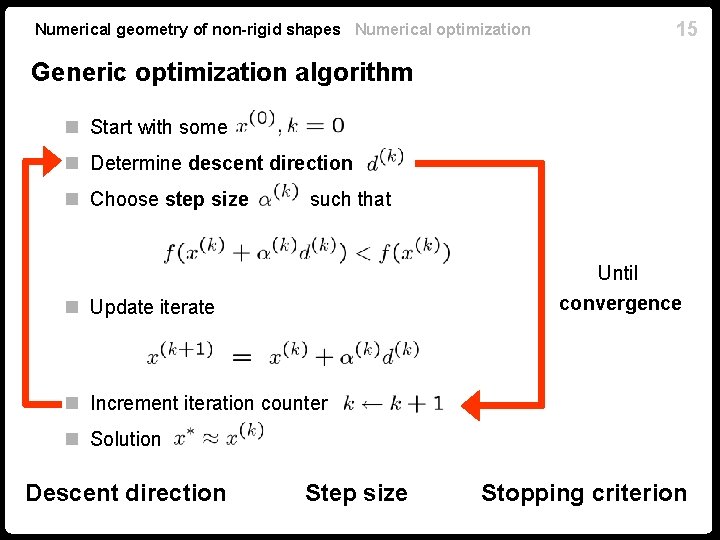
Numerical geometry of non-rigid shapes Numerical optimization 15 Generic optimization algorithm n Start with some n Determine descent direction n Choose step size such that Until convergence n Update iterate n Increment iteration counter n Solution Descent direction Step size Stopping criterion

16 Numerical geometry of non-rigid shapes Numerical optimization Stopping criteria n Near local minimum, (or equivalently Stop when gradient norm becomes small n Stop when step size becomes small n Stop when relative objective change becomes small )

Numerical geometry of non-rigid shapes Numerical optimization 17 Line search Optimal step size can be found by solving a one-dimensional optimization problem One-dimensional optimization algorithms for finding the optimal step size are generically called exact line search

Numerical geometry of non-rigid shapes Numerical optimization Armijo [ar-mi-xo] rule The function sufficiently decreases if Armijo rule (Larry Armijo, 1966): start with multiplying by some and decrease it by until the function sufficiently decreases 18

Numerical geometry of non-rigid shapes Numerical optimization Descent direction How to descend in the fastest way? Go in the direction in which the height lines are the densest Devil’s Tower Topographic map 19

Numerical geometry of non-rigid shapes Numerical optimization Steepest descent Directional derivative: how much changes in the direction (negative for a descent direction) Find a unit-length direction minimizing directional derivative 20

Numerical geometry of non-rigid shapes Numerical optimization 21 Steepest descent L 2 norm Normalized steepest descent L 1 norm Coordinate descent (coordinate axis in which descent is maximal)

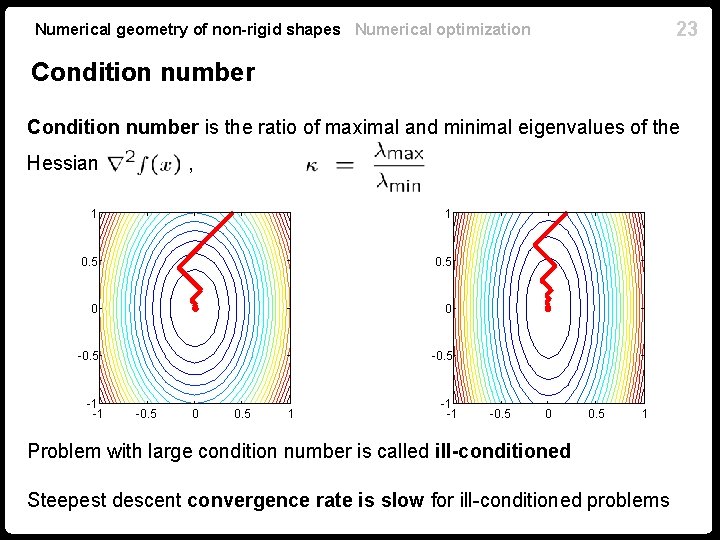
23 Numerical geometry of non-rigid shapes Numerical optimization Condition number is the ratio of maximal and minimal eigenvalues of the Hessian , 1 1 0. 5 0 0 -0. 5 -1 -1 -0. 5 0 0. 5 1 Problem with large condition number is called ill-conditioned Steepest descent convergence rate is slow for ill-conditioned problems

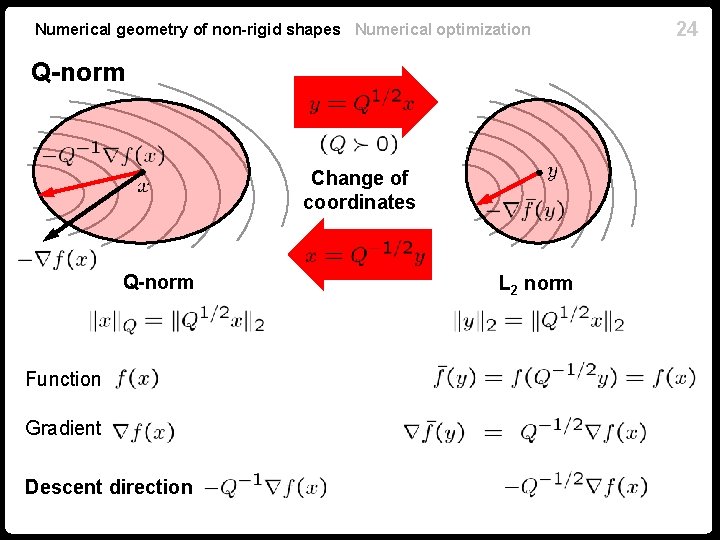
Numerical geometry of non-rigid shapes Numerical optimization Q-norm Change of coordinates Q-norm Function Gradient Descent direction L 2 norm 24

Numerical geometry of non-rigid shapes Numerical optimization Preconditioning Using Q-norm for steepest descent can be regarded as a change of coordinates, called preconditioning Preconditioner should be chosen to improve the condition number of the Hessian in the proximity of the solution In system of coordinates, the Hessian at the solution is (a dream) 25

26 Numerical geometry of non-rigid shapes Numerical optimization Newton method as optimal preconditioner Best theoretically possible preconditioner , giving descent direction Ideal condition number Problem: the solution is unknown in advance Newton direction: use Hessian as a preconditioner at each iteration

27 Numerical geometry of non-rigid shapes Numerical optimization Another derivation of the Newton method Approximate the function as a quadratic function using second-order Taylor expansion (quadratic function in ) Close to solution the function looks like a quadratic function; the Newton method converges fast

Numerical geometry of non-rigid shapes Numerical optimization Frozen Hessian Observation: close to the optimum, the Hessian does not change significantly Reduce the number of Hessian inversions by keeping the Hessian from previous iterations and update it once in a few iterations Such a method is called Newton with frozen Hessian 29

Numerical geometry of non-rigid shapes Numerical optimization 30 Cholesky factorization Decompose the Hessian where is a lower triangular matrix Solve the Newton system in two steps Andre Louis Cholesky (1875 -1918) n Forward substitution n Backward substitution Complexity: , better than straightforward matrix inversion

Numerical geometry of non-rigid shapes Numerical optimization 31 Truncated Newton Solve the Newton system approximately A few iterations of conjugate gradients or other algorithm for the solution of linear systems can be used Such a method is called truncated or inexact Newton

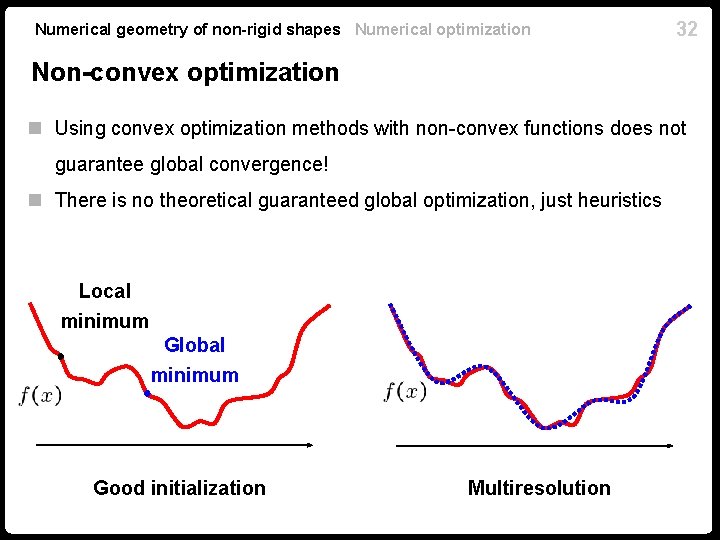
Numerical geometry of non-rigid shapes Numerical optimization 32 Non-convex optimization n Using convex optimization methods with non-convex functions does not guarantee global convergence! n There is no theoretical guaranteed global optimization, just heuristics Local minimum Global minimum Good initialization Multiresolution

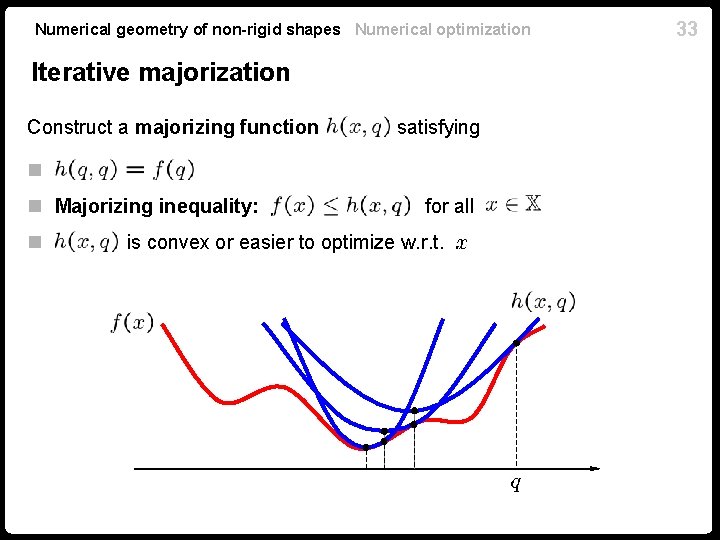
Numerical geometry of non-rigid shapes Numerical optimization Iterative majorization Construct a majorizing function satisfying n. n Majorizing inequality: n for all is convex or easier to optimize w. r. t. 33

Numerical geometry of non-rigid shapes Numerical optimization 34 Iterative majorization n Start with some n Find such that n Update iterate n Increment iteration counter n Solution Until convergence

Numerical geometry of non-rigid shapes Numerical optimization Constrained optimization MINEFIELD CLOSED ZONE 35

Numerical geometry of non-rigid shapes Numerical optimization 36 Constrained optimization problems Generic constrained minimization problem where n are inequality constraints n are equality constraints n A subset of the search space in which the constraints hold is called feasible set n A point belonging to the feasible set is called a feasible solution A minimizer of the problem may be infeasible!

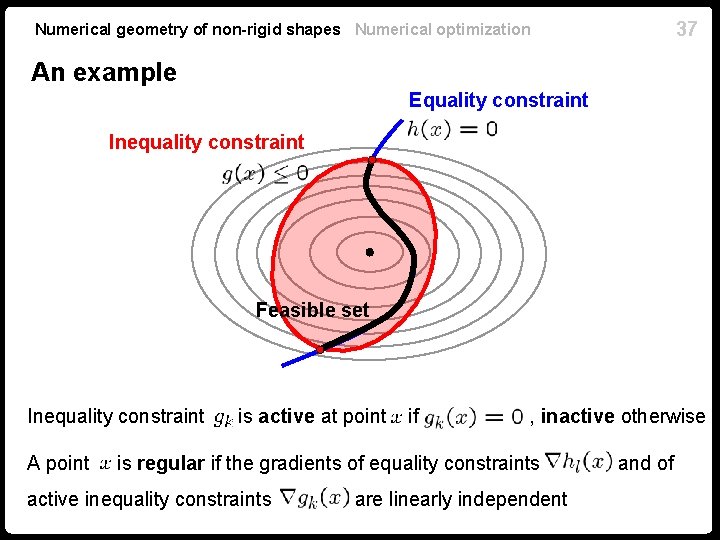
37 Numerical geometry of non-rigid shapes Numerical optimization An example Equality constraint Inequality constraint Feasible set Inequality constraint A point is active at point if , inactive otherwise is regular if the gradients of equality constraints active inequality constraints are linearly independent and of

Numerical geometry of non-rigid shapes Numerical optimization Lagrange multipliers Main idea to solve constrained problems: arrange the objective and constraints into a single function and minimize it as an unconstrained problem is called Lagrangian and are called Lagrange multipliers 38

Numerical geometry of non-rigid shapes Numerical optimization 39 KKT conditions If is a regular point and a local minimum, there exist Lagrange multipliers and n n such that for all such that and for active constraints and zero for inactive constraints n Known as Karush-Kuhn-Tucker conditions Necessary but not sufficient! for all

40 Numerical geometry of non-rigid shapes Numerical optimization KKT conditions Sufficient conditions: If the objective is convex, the inequality constraints and the equality constraints are convex are affine, the KKT conditions are sufficient In this case, minimizer) is the solution of the constrained problem (global constrained

Numerical geometry of non-rigid shapes Numerical optimization 41 Geometric interpretation Consider a simpler problem: Equality constraint The gradient of objective and constraint must line up at the solution

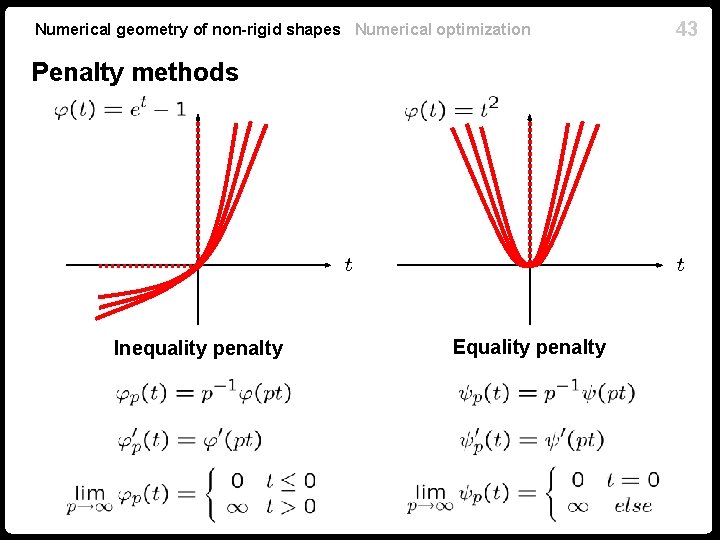
Numerical geometry of non-rigid shapes Numerical optimization 42 Penalty methods Define a penalty aggregate where and For larger values of the parameter is stronger are parametric penalty functions , the penalty on the constraint violation

Numerical geometry of non-rigid shapes Numerical optimization Penalty methods Inequality penalty Equality penalty 43

Numerical geometry of non-rigid shapes Numerical optimization 44 Penalty methods n Start with some and initial value of n Find by solving an unconstrained optimization problem initialized with n Set n Update n Solution Until convergence