Numerical geometry of nonrigid shapes Differential geometry 1

Numerical geometry of non-rigid shapes Differential geometry 1 Differential geometry II Lecture 2 © Alexander & Michael Bronstein tosca. cs. technion. ac. il/book Numerical geometry of non-rigid shapes Stanford University, Winter 2009

2 Numerical geometry of non-rigid shapes Differential geometry Intrinsic & extrinsic geometry n First fundamental form describes completely the intrinsic geometry. n Second fundamental form describes completely the extrinsic geometry – the “layout” of the shape in ambient space. n First fundamental form is invariant to isometry. n Second fundamental form is invariant to rigid motion (congruence). n If and are congruent (i. e. , ), then they have identical intrinsic and extrinsic geometries. n Fundamental theorem: a map preserving the first and the second fundamental forms is a congruence. Said differently: an isometry preserving second fundamental form is a restriction of Euclidean isometry.

Numerical geometry of non-rigid shapes Differential geometry An intrinsic view n Our definition of intrinsic geometry (first fundamental form) relied so far on ambient space. n Can we think of our surface as of an abstract manifold immersed nowhere? n What ingredients do we really need? n Smooth two-dimensional manifold n Tangent space at each point. n Inner product n These ingredients do not require any ambient space! 3

Numerical geometry of non-rigid shapes Differential geometry Riemannian geometry n Riemannian metric: bilinear symmetric positive definite smooth map n Abstract inner product on tangent space of an abstract manifold. n Coordinate-free. n In parametrization coordinates is expressed as first fundamental form. n A farewell to extrinsic geometry! Bernhard Riemann (1826 -1866) 4

Numerical geometry of non-rigid shapes Differential geometry An intrinsic view n We have two alternatives to define the intrinsic metric using the path length. n Extrinsic definition: n Intrinsic definition: n The second definition appears more general. 5

Numerical geometry of non-rigid shapes Differential geometry Nash’s embedding theorem n Embedding theorem (Nash, 1956): any Riemannian metric can be realized as an embedded surface in Euclidean space of sufficiently high yet finite dimension. n Technical conditions: n Manifold is n For an -dimensional manifold, embedding space dimension is John Forbes Nash (born 1928) n Practically: intrinsic and extrinsic views are equivalent! 6

Numerical geometry of non-rigid shapes Differential geometry Uniqueness of the embedding n Nash’s theorem guarantees existence of embedding. n It does not guarantee uniqueness. n Embedding is clearly defined up to a congruence. n Are there cases of non-trivial non-uniqueness? Formally: n Given an abstract Riemannian manifold , and an embedding , does there exist another embedding such that and are incongruent? Said differently: Do isometric yet incongruent shapes exist? 7

8 Numerical geometry of non-rigid shapes Differential geometry Bending n Shapes admitting incongruent isometries are called bendable. n Plane is the simplest example of a bendable surface. n Bending: an isometric deformation transforming into .

Numerical geometry of non-rigid shapes Differential geometry Bending and rigidity n Existence of two incongruent isometries guarantee that does not can be physically folded into without the need to cut or glue. n If there exists a family of bendings w. r. t. such that and continuous , the shapes are called continuously bendable or applicable. n Shapes that do not have incongruent isometries are rigid. n Extrinsic geometry of a rigid shape is fully determined by the intrinsic one. 9

Numerical geometry of non-rigid shapes Differential geometry Alice’s wonders in the Flatland n Subsets of the plane: n Second fundamental form vanishes everywhere n Isometric shapes and have identical first and second fundamental forms n Fundamental theorem: and congruent. Flatland is rigid! are 10

Numerical geometry of non-rigid shapes Differential geometry Rigidity conjecture If the faces of a polyhedron were made of metal plates and the polyhedron edges were replaced by hinges, the polyhedron would be rigid. In practical applications shapes are represented as polyhedra (triangular meshes), so… Leonhard Euler (1707 -1783) Do non-rigid shapes really exist? 11

Numerical geometry of non-rigid shapes Differential geometry Rigidity conjecture timeline 1766 Euler’s Rigidity Conjecture: every polyhedron is rigid 1813 Cauchy: every convex polyhedron is rigid 1927 Cohn-Vossen: all surfaces with positive Gaussian curvature are rigid 1974 Gluck: almost all simply connected surfaces are rigid 1977 Connelly finally disproves Euler’s conjecture 12

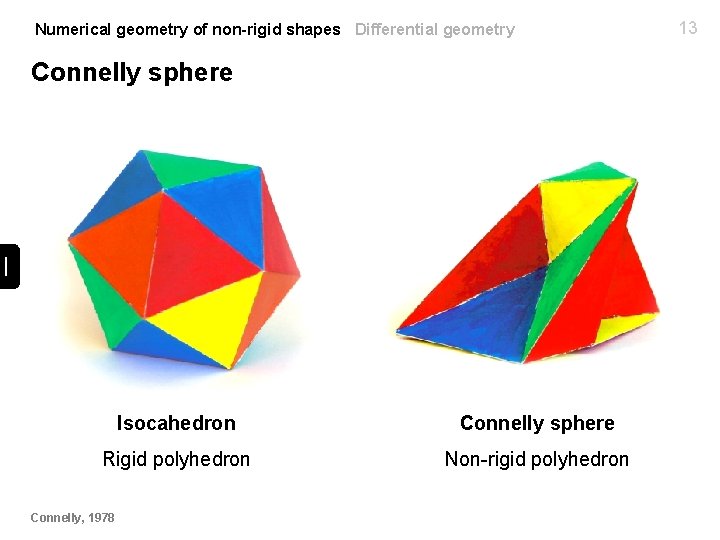
Numerical geometry of non-rigid shapes Differential geometry Connelly sphere Isocahedron Connelly sphere Rigid polyhedron Non-rigid polyhedron Connelly, 1978 13

Numerical geometry of non-rigid shapes Differential geometry 14 “Almost rigidity” n Most of the shapes (especially, polyhedra) are rigid. n This may give the impression that the world is more rigid than non-rigid. n This is probably true, if isometry is considered in the strict sense n Many objects have some elasticity and therefore can bend almost Isometrically n No known results about “almost rigidity” of shapes.

Numerical geometry of non-rigid shapes Differential geometry Gaussian curvature – a second look n Gaussian curvature measures how a shape is different from a plane. n We have seen two definitions so far: n Product of principal curvatures: n Determinant of shape operator: n Both definitions are extrinsic. Here is another one: n For a sufficiently small of a metric ball of radius , perimeter is given by 15

Numerical geometry of non-rigid shapes Differential geometry Gaussian curvature – a second look n Riemannian metric is locally Euclidean up to second order. n Third order error is controlled by Gaussian curvature. n Gaussian curvature n measures the defect of the perimeter, i. e. , how is different from the Euclidean . n positively-curved surface – perimeter smaller than Euclidean. n negatively-curved surface – perimeter larger than Euclidean. 16

Numerical geometry of non-rigid shapes Differential geometry 17 Theorema egregium n Our new definition of Gaussian curvature is intrinsic! n Gauss’ Remarkable Theorem …formula itaque sponte perducit ad egregium theorema: si superficies curva in quamcunque aliam superficiem explicatur, mensura curvaturae in singulis punctis invariata manet. In modern words: n Gaussian curvature is invariant to isometry. Karl Friedrich Gauss (1777 -1855)

Numerical geometry of non-rigid shapes Differential geometry An Italian connection… 18

Numerical geometry of non-rigid shapes Differential geometry Intrinsic invariants n Gaussian curvature is a local invariant. n Isometry invariant descriptor of shapes. n Problems: n Second-order quantity – sensitive to noise. n Local quantity – requires correspondence between shapes. 19

Numerical geometry of non-rigid shapes Differential geometry 20 Gauss-Bonnet formula n Solution: integrate Gaussian curvature over the whole shape n is Euler characteristic. n Related genus by n Stronger topological rather than geometric invariance. n Result known as Gauss-Bonnet formula. Pierre Ossian Bonnet (1819 -1892)

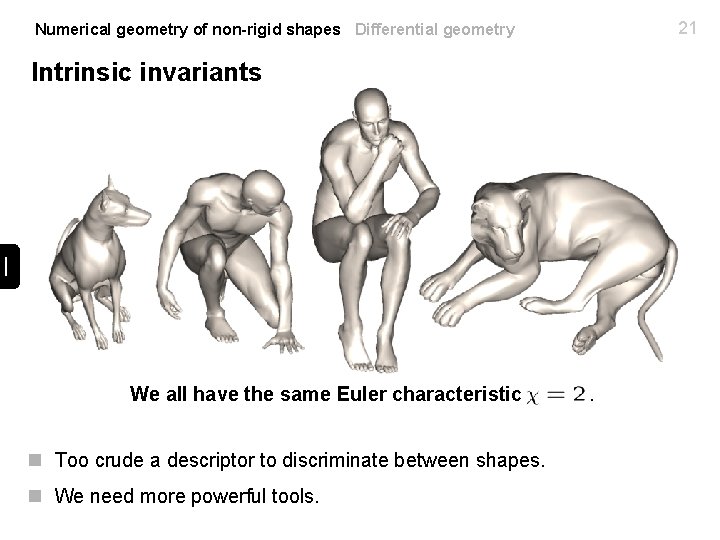
21 Numerical geometry of non-rigid shapes Differential geometry Intrinsic invariants We all have the same Euler characteristic n Too crude a descriptor to discriminate between shapes. n We need more powerful tools. .