Differential Equations Ordinary differential equation ODE Partial differential

Differential Equations

Ordinary differential equation (ODE) , Partial differential equation (PDE) ØOrder : highest derivative in equation

Linear equation, nonlinear equation

Differential equations l Ordinary differential equation (ODE) , Partial differential equation (PDE) l Order : highest derivative in equation Linear equation, nonlinear equation l

Differential equations l Homogeneous equation, nonhomogeneous equation l Implicit solution, explicit solution

Differential equations l General solution, particular solution l Initial value problem, boundary value problem l Exact, approximate, and numerical solutions

First order differential equation, I l Separable equations; l Equations reducible to separable form;

First order differential equation, I l Exact differential equations; l Integrating factor; if ODE is not exact, it can be made exact.

First order differential equation, II l Linear first-order differential equation (homogeneous); l Linear first-order differential equation (nonhomogeneous);

First order differential equation, II l Method of variation of parameters l General solution of homogeneous eq. is given by l Idea is that we may replace the integration constant c by u(x)

Ordinary Linear differential equation, I l Second order linear differential equation, l Theorem (Superposition Principle): Any linear combination of solutions of the homogeneous linear differential equation is also a solution.

Ordinary Linear differential equation, I l Homogeneous 2 nd order ODE with constant cocefficients l Try Characteristic equation (or auxiliary equation) l l Roots: Solutions: Examples:

Ordinary Linear differential equation, II l Two functions are linearly dependent if they are proportional. l Theorem: If y 1 and y 2 are linearly independent solutions of ODE, the general solution of ODE is If 1 2, general solution is l l If 1, 2 are complex conjugate, the solutions are complex

Ordinary Linear differential equation, II l Real solutions from these complex solutions by Euler formulas: l Corresponding general solution: l Example: initial value problem:

Ordinary Linear differential equation, III l Double root case (critical case) l Second solution by method of variation of parameters l Corresponding general solution:

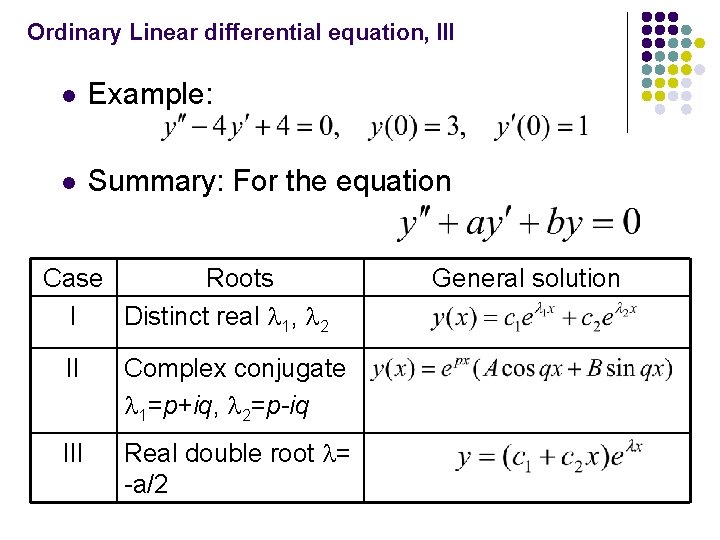
Ordinary Linear differential equation, III l Example: l Summary: For the equation Case Roots I Distinct real 1, 2 II Complex conjugate 1=p+iq, 2=p-iq III Real double root = -a/2 General solution

Ordinary Linear differential equation, IV l Cauchy equation( or Euler equation) l Try y = xm l The general solution is l Example: Critical case: l

Nonhomogeneous linear equations l Theorem: A general solution y(x) of the linear nonhomogeneous differential equation l is the sum of a general solution yh(x) of the corresponding homogeneous equation and an arbitrary particular solution yp(x)

Nonhomogeneous linear equations l Method of variation of parameters: l Example: