Numerical modeling of rock deformation 14 FEM 2

Folding: Mechanism Single-layer folds are presumably the best studied fold types. Natural single-layer folds

Folding: Linear stability analysis Pure shear shortening causes homogeneous thickening. Basic state - no

Folding: Linear stability analysis Thin-plate equation for viscous folding. Partial differential equation. x Is

The analytical solution for the growth rate a of the wavelength components is The

Plot the analytical growth rate and the numerical growth rate for different values of

Numerical verification ~l 1 Dispersion curve a 1 Biot, 1957 Ramberg, 1963 l 1

This is what you should get Viscosity ratio = 100 Numerical modeling of rock

Slides: 8

Download presentation

Numerical modeling of rock deformation: 14 FEM 2 D Viscous folding Stefan Schmalholz schmalholz@erdw. ethz. ch NO E 61 AS 2008, Thursday 10 -12, NO D 11 Numerical modeling of rock deformation, Stefan Schmalholz, ETH Zurich

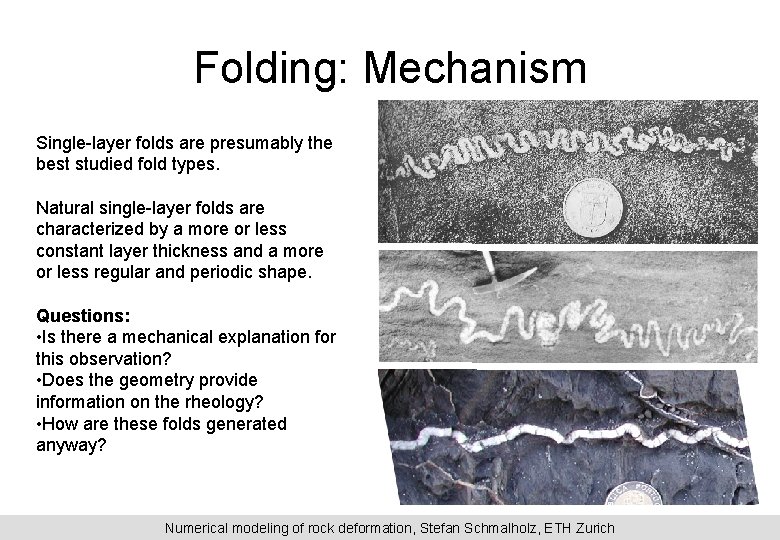
Folding: Mechanism Single-layer folds are presumably the best studied fold types. Natural single-layer folds are characterized by a more or less constant layer thickness and a more or less regular and periodic shape. Questions: • Is there a mechanical explanation for this observation? • Does the geometry provide information on the rheology? • How are these folds generated anyway? Numerical modeling of rock deformation, Stefan Schmalholz, ETH Zurich

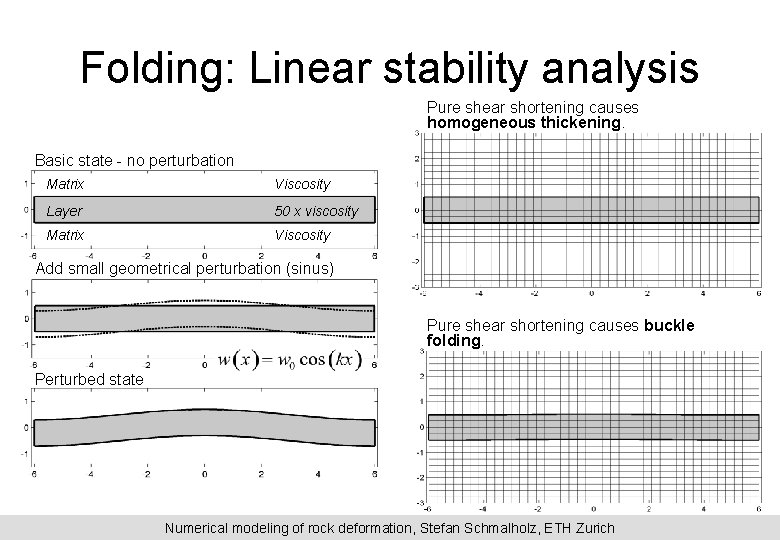
Folding: Linear stability analysis Pure shear shortening causes homogeneous thickening. Basic state - no perturbation Matrix Viscosity Layer 50 x viscosity Matrix Viscosity Add small geometrical perturbation (sinus) Pure shear shortening causes buckle folding. Perturbed state Numerical modeling of rock deformation, Stefan Schmalholz, ETH Zurich

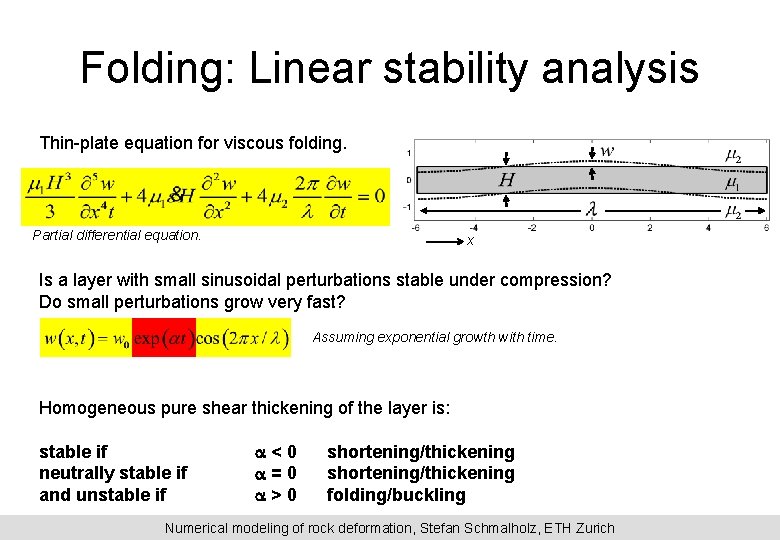
Folding: Linear stability analysis Thin-plate equation for viscous folding. Partial differential equation. x Is a layer with small sinusoidal perturbations stable under compression? Do small perturbations grow very fast? Assuming exponential growth with time. Homogeneous pure shear thickening of the layer is: stable if neutrally stable if and unstable if a<0 a=0 a>0 shortening/thickening folding/buckling Numerical modeling of rock deformation, Stefan Schmalholz, ETH Zurich

The analytical solution for the growth rate a of the wavelength components is The analytical form for the amplitude, w, evolution considering the background shortening rate is The numerical form for the amplitude evolution is The growth rate can be calculated from the numerically calculated amplitude Numerical modeling of rock deformation, Stefan Schmalholz, ETH Zurich

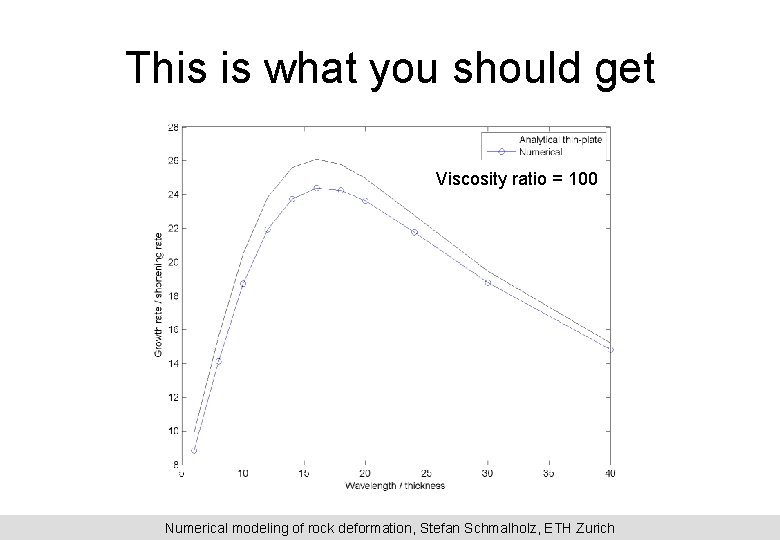
Plot the analytical growth rate and the numerical growth rate for different values of the wavelength (model width). Tips: -make a loop that changes the model width (i. e. wavelength) automatically -Only make one time step -Use a small time step and a small initial amplitude -You can extract the layer interface from the YCOORD array with the vector Ind_lay. Test the formulas for the maximal value of the growth rate and for the dominant wavelength, i. e. the wavelength for which the growth rate is maximal. Such tests are very important to test numerical algorithms and evaluate their accuracy. The analytical solution is an approximate, thin-plate solution, because it neglects the shear deformation and shear strains during folding. Describe the difference between the analytical and numerical solution and explain them. You can also add a random perturbation on the layer interface and test whether the resulting fold shapes are close to the ones predicted by the analytical solution, such as on the next page. Numerical modeling of rock deformation, Stefan Schmalholz, ETH Zurich

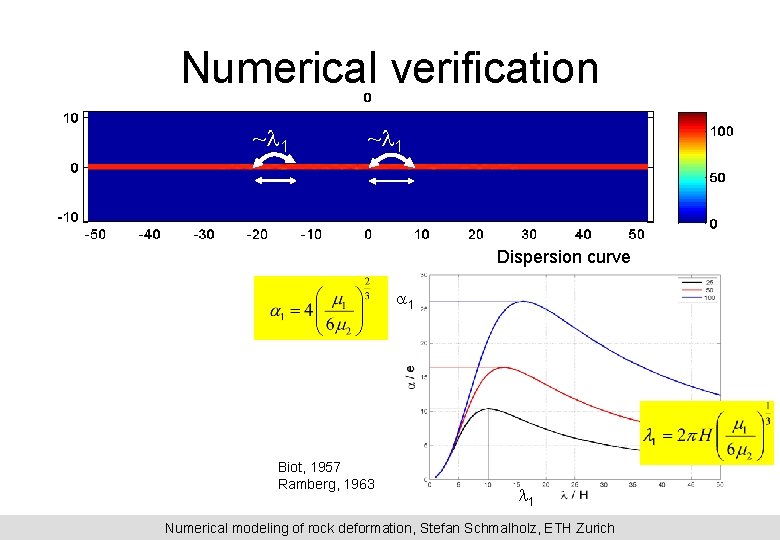
Numerical verification ~l 1 Dispersion curve a 1 Biot, 1957 Ramberg, 1963 l 1 Numerical modeling of rock deformation, Stefan Schmalholz, ETH Zurich

This is what you should get Viscosity ratio = 100 Numerical modeling of rock deformation, Stefan Schmalholz, ETH Zurich