Differential Geometry Computer Vision 8 Differential Geometry 1


















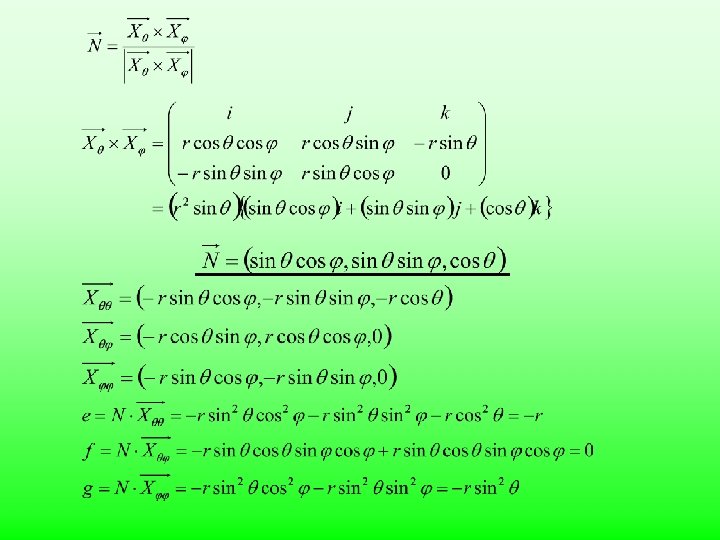








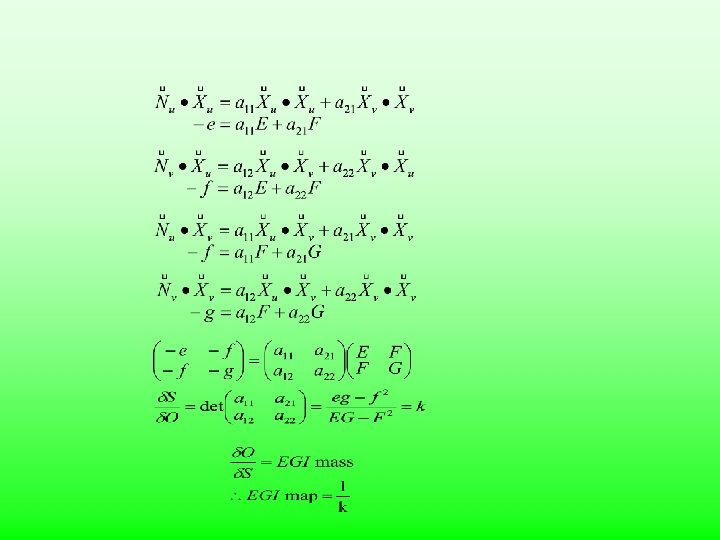









- Slides: 41

Differential Geometry Computer Vision #8

Differential Geometry 1. Curvature of curve 2. Curvature of surface 3. Application of curvature

Parameterization of curve 1. curve -- s arc length s a(s) = ( x(s), y(s) ) a(s) 2. tangent of a curve a’(s) = ( x’(s), y’(s) ) 3. curvature of a curve a”(s) = ( x”(s), y”(s) ) |a”(s)| -- curvature

Example (circle) 1. Arc length, s 2. coordinates 3. tangent 4. curvature

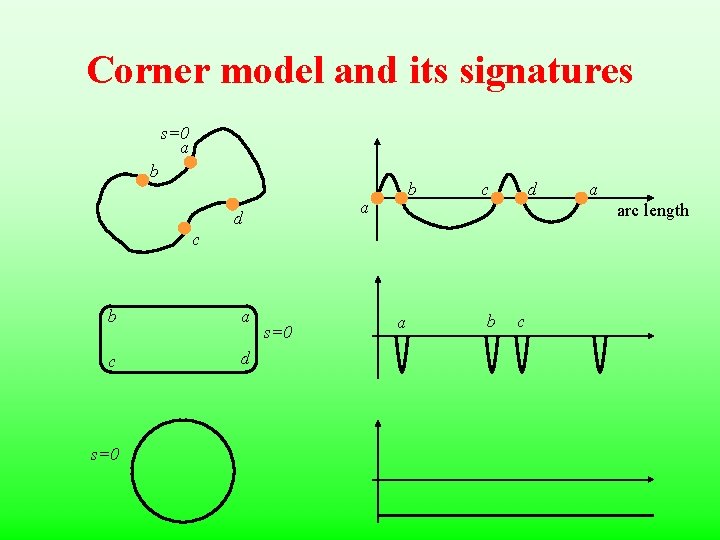
Definition of curvature The normal direction (n) toward the empty side.

Corner model and its signatures s=0 a b b a d c d arc length c b a c d s=0 a a b c

Gaussian filter and scale space a + a b + + b a c f d e d c h g i j e k

Curvature of surfaces normal section normal curvature non-normal section Principal directions and principal curvatures

Principal curvatures plane: all directions sphere: all directions cylinder: ellipsoid: hyperboloid:

Gaussian curvature and mean curvature

Parabolic points Parabolic point elliptic point hyperbolic point F. Klein used the parabolic curves for a peculiar investigation. To test his hypothesis that the artistic beauty of a face was based on certain mathematical relation, he has all the parabolic curves marked out on the Apollo Belvidere. But the curves did not possess a particularly simpler form, nor did they follow any general law that could be discerned.



Lines of curvature Principal directions, which gives the maximum and the minimal normal curvature. Principal direction curves along principal directions PD PD PD

Lines of curvature

Curvature primal sketches along lines of curvature

Important formula 1. Surface 2. surface normal 3. the first fundamental form 4. the second fundamental form


Z Y X
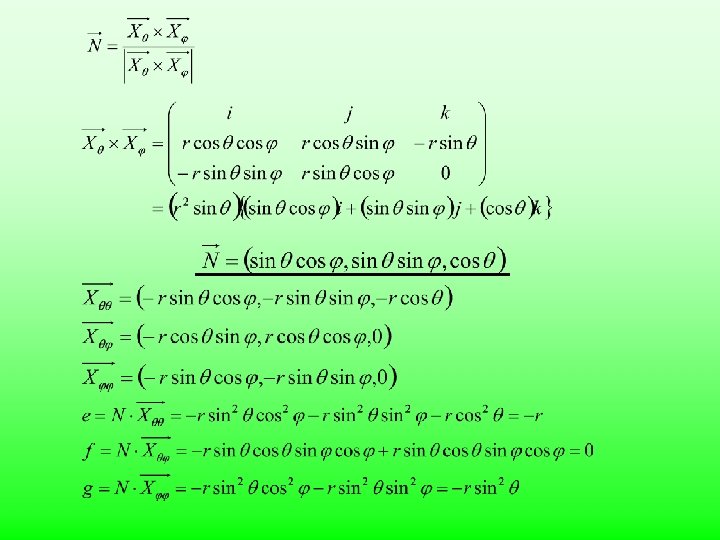


Summary 1. curvature of curve 2. curvature of surface – Gaussian curvature – mean curvature

Surface Description #2 (Extended Gaussian Image)

Topics 1. Gauss map 2. Extended Gaussian Image 3. Application of EGI

Gauss map gauss map 1 D gauss map Let S⊂R 3 be a surface with an orientation N. The map N: S→R 3 takes its values in the unit sphere The map N: S→S 3 is called the Gauss map. 2 D

Characteristics of EGI u. EGI is the necessary and the sufficient condition for the congruence of two convex polyhedra. u. Ratio between the area on the Gaussian sphere and the area on the object is equal to Gaussian curvature. u. EGI mass on the sphere is the inverse of Gaussian curvature. u. Mass center of EGI is at the origin of the sphere u. An object rotates, then EGI of the object also rotates. However, both rotations are same.

Relationship between EGI and Gaussian curvature object Gaussian sphere small large small (K: small) small (K: large) large

Gaussian curvature and EGI maps u u Since and exist on the tangential plane at , we can represent them by a linear combination of and
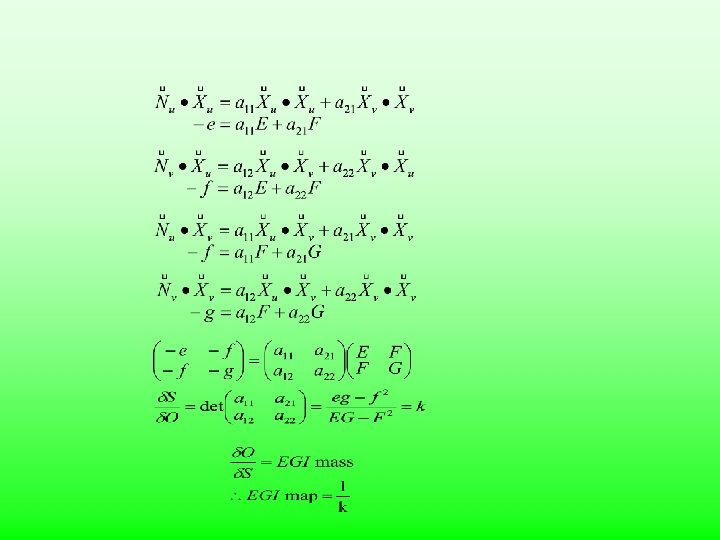

Implementation of EGI Tessellation of the unit sphere • all cells should have the same area have the same shape occur in a regular pattern • geodesic dome based on a regular polyhedron semi-regular geodesic dome

Example of EGI side view top view Cylinder Ellipsoid

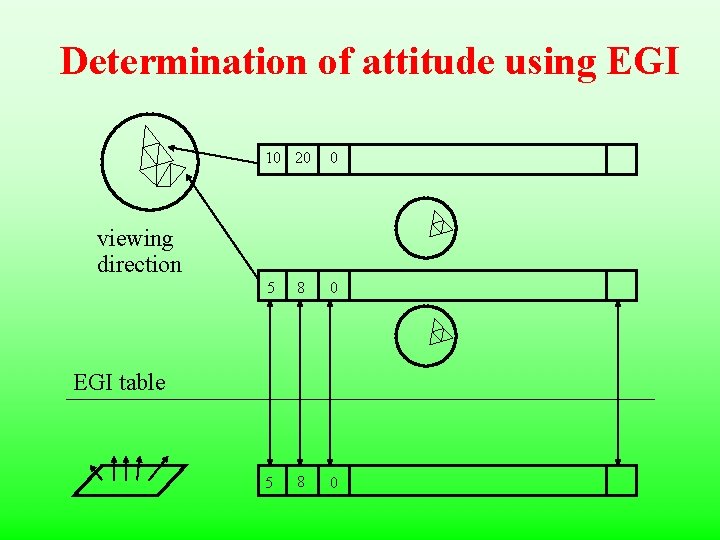
Determination of attitude using EGI 10 20 0 5 8 0 viewing direction EGI table

The complex EGI(CEGI) Normal distance and area of a 3 -D object are encoded as a complex weight. Pnk associated with the surface normal nk such that:

The complex EGI(CEGI) Gauss mapping Origin (a) Cube (b) CEGI of cube (note: The weight is shown only for normal n 1 for clearly. )



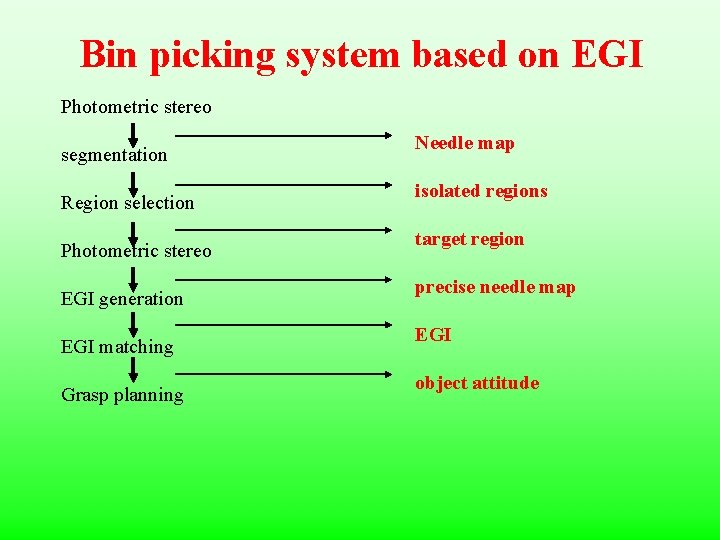
Bin picking system based on EGI Photometric stereo segmentation Region selection Photometric stereo EGI generation EGI matching Grasp planning Needle map isolated regions target region precise needle map EGI object attitude

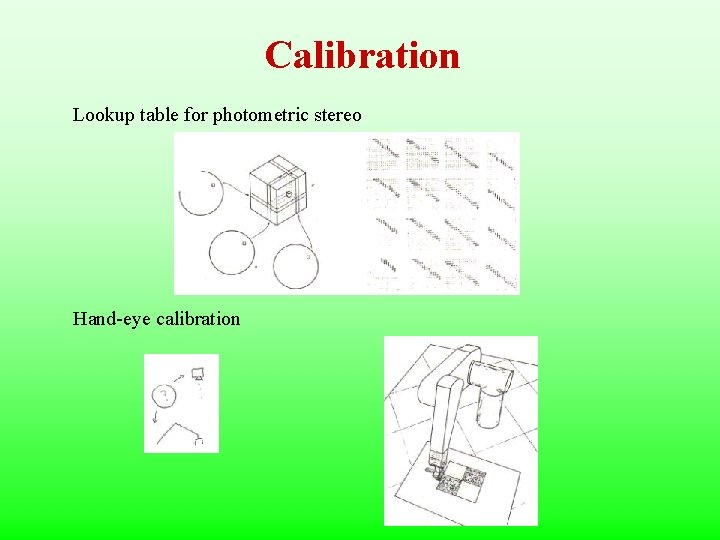
Calibration Lookup table for photometric stereo Hand-eye calibration

Photometric Stereo Set-up

Bin-Picking System

Summary 1. Gauss map 2. Extended Gaussian Image 3. Characteristics of EGI congruence of two convex polyhedra EGI mass is the inverse of Gaussian curvature mass center of EGI is at the origin of the sphere 4. Implementation of EGI Tessellation of the unit sphere Recognition using EGI 5. Complex EGI 6. Bin-picking system based on EGI 7. Read Horn pp. 365 -39 pp. 423 -451
 Cs766
Cs766 Multiple view geometry tutorial
Multiple view geometry tutorial Quadrifocal
Quadrifocal Multiple view geometry in computer vision solution manual
Multiple view geometry in computer vision solution manual Epipolar geometry computer vision
Epipolar geometry computer vision Epipolar geometry computer vision
Epipolar geometry computer vision Weingarten equation in differential geometry
Weingarten equation in differential geometry Differential geometry
Differential geometry 1-form differential geometry
1-form differential geometry Normal curvature
Normal curvature Lewis dot structure and molecular geometry
Lewis dot structure and molecular geometry Electron domain geometry vs molecular geometry
Electron domain geometry vs molecular geometry Bonding theories
Bonding theories Classification of pde examples
Classification of pde examples Dda computer graphics
Dda computer graphics 16-385 cmu
16-385 cmu Kalman filter computer vision
Kalman filter computer vision T11 computer
T11 computer Berkeley computer vision
Berkeley computer vision Computer vision vs image processing
Computer vision vs image processing Radiometry in computer vision
Radiometry in computer vision Linear algebra for computer vision
Linear algebra for computer vision Computer vision
Computer vision Computer vision
Computer vision Watershed segmentation
Watershed segmentation Cs223 stanford
Cs223 stanford Python azure cognitive services
Python azure cognitive services Mathematical foundations of computer graphics and vision
Mathematical foundations of computer graphics and vision Computer vision slides
Computer vision slides Caffe computer vision
Caffe computer vision Computer vision final exam
Computer vision final exam Sift computer vision
Sift computer vision Computer vision: models, learning, and inference
Computer vision: models, learning, and inference Computer vision models learning and inference pdf
Computer vision models learning and inference pdf Geometric camera calibration
Geometric camera calibration Computer
Computer Computer vision vs nlp
Computer vision vs nlp Zed camera calibration
Zed camera calibration Computer vision
Computer vision Sampling in computer vision
Sampling in computer vision Computer vision
Computer vision Computer vision
Computer vision