Numerical geometry of nonrigid shapes Geometry Numerical geometry

Numerical geometry of non-rigid shapes Geometry Numerical geometry of non-rigid shapes Shortest path problems Alexander Bronstein, Michael Bronstein, Ron Kimmel © 2007 All rights reserved 1

Numerical geometry of non-rigid shapes Geometry Alexander Bronstein, Michael Bronstein, Ron Kimmel © 2007 All rights reserved 2

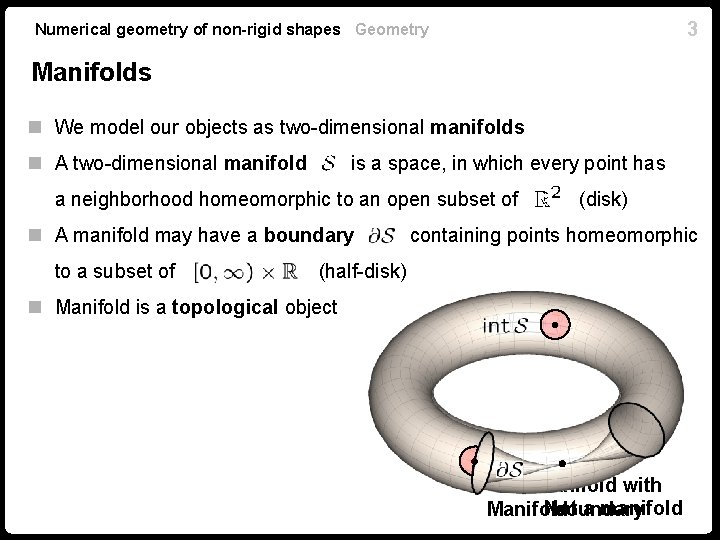
3 Numerical geometry of non-rigid shapes Geometry Manifolds n We model our objects as two-dimensional manifolds n A two-dimensional manifold is a space, in which every point has a neighborhood homeomorphic to an open subset of (disk) n A manifold may have a boundary containing points homeomorphic to a subset of (half-disk) n Manifold is a topological object Manifold with Not a manifold Manifold boundary

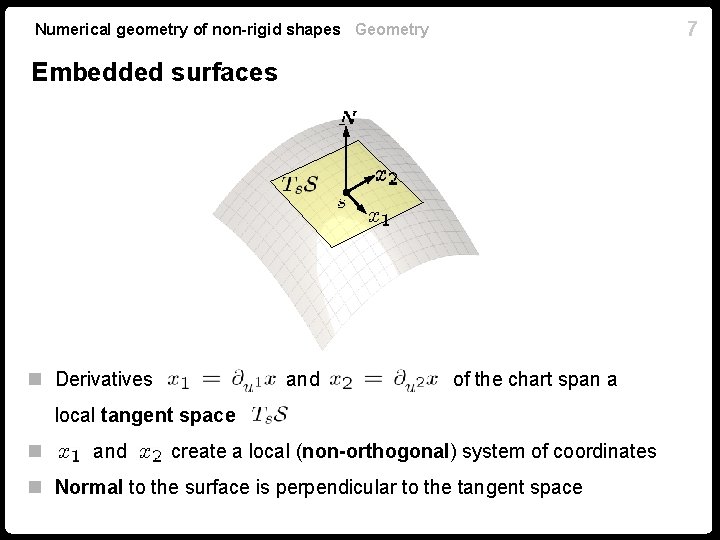
Numerical geometry of non-rigid shapes Geometry Embedded surfaces n Surface of a tangible physical object is a two-dimensional manifold n Surface is embedded in the ambient Euclidean space n We can often create a smooth local system of coordinates (chart) for some portion of the surface n Parametric surface: a single system of coordinates in some parametrization domain is available for the entire surface 5

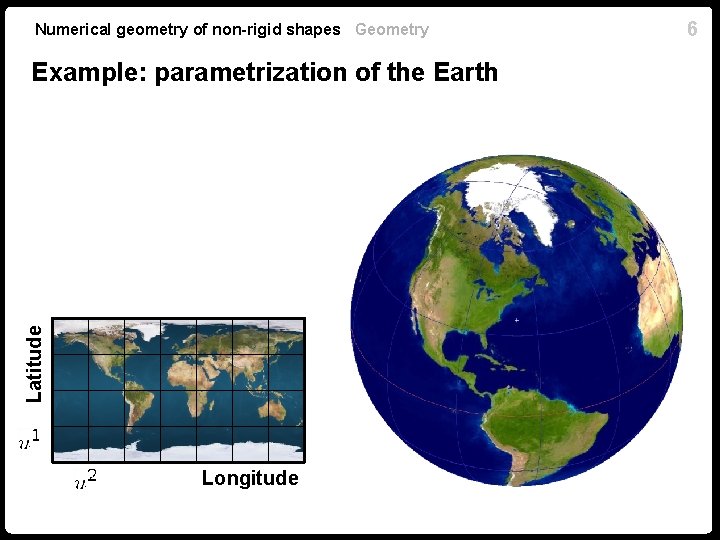
Numerical geometry of non-rigid shapes Geometry Example: parametrization of the Earth Latitude Longitude 6

Numerical geometry of non-rigid shapes Geometry Embedded surfaces n Derivatives and of the chart span a local tangent space n and create a local (non-orthogonal) system of coordinates n Normal to the surface is perpendicular to the tangent space 7

Numerical geometry of non-rigid shapes Geometry Metric n To create a geometry, we need the ability to measure distance n Formally, we define a metric n There are many ways to define a metric on n Restricted metric: measure Euclidean distance in ambient space n Defines extrinsic geometry – the way the surface is laid out in ambient space 8

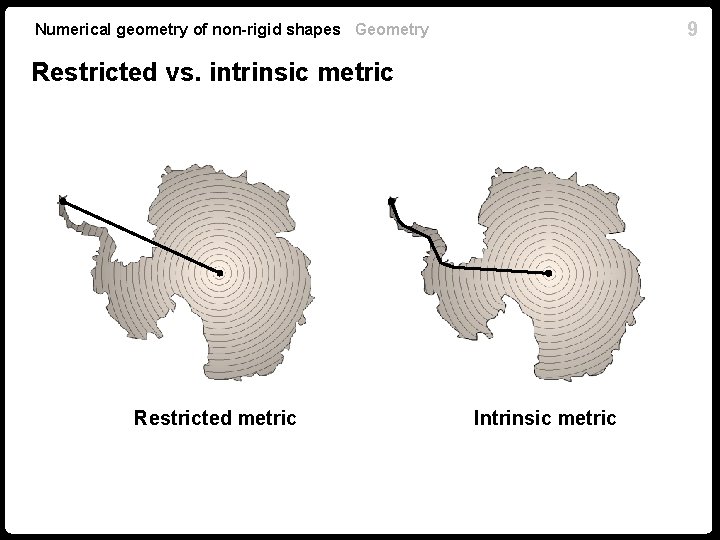
9 Numerical geometry of non-rigid shapes Geometry Restricted vs. intrinsic metric Restricted metric Intrinsic metric

Numerical geometry of non-rigid shapes Geometry 10 Metric n Induced or intrinsic metric: measure the shortest path length on the surface where is a path with n Defines intrinsic geometry, experienced by a bug living on the surface and not knowing about the ambient space n The space is called complete if the shortest path exists n Shortest path realizing is called minimal geodesic

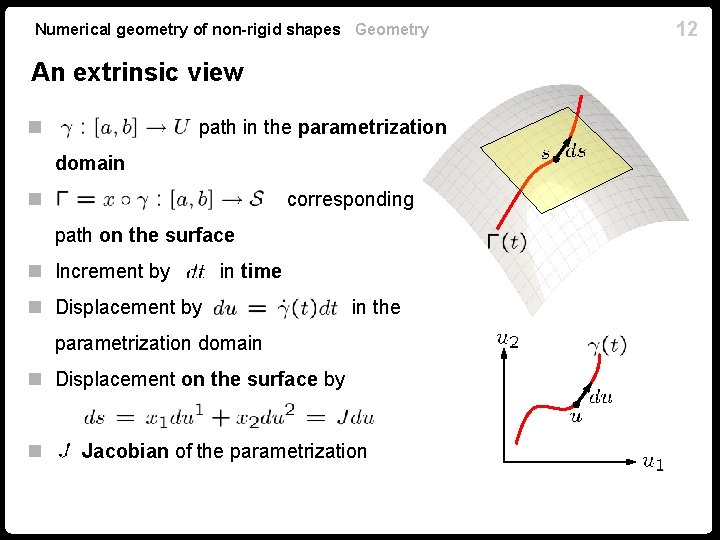
Numerical geometry of non-rigid shapes Geometry An extrinsic view n path in the parametrization domain n corresponding path on the surface n Increment by in time n Displacement by in the parametrization domain n Displacement on the surface by n Jacobian of the parametrization 12

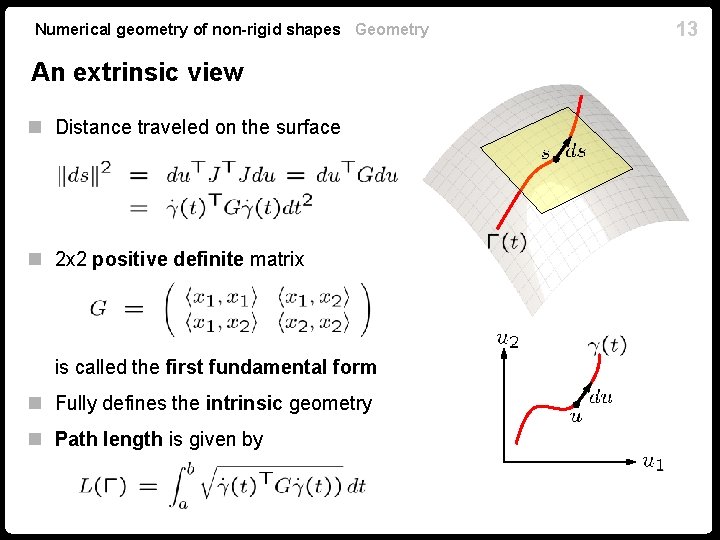
Numerical geometry of non-rigid shapes Geometry An extrinsic view n Distance traveled on the surface n 2 x 2 positive definite matrix is called the first fundamental form n Fully defines the intrinsic geometry n Path length is given by 13

Numerical geometry of non-rigid shapes Geometry 14 An intrinsic view n In our definitions so far, intrinsic geometry relied on the ambient space n Instead, think of our object as an abstract manifold immersed nowhere n We define a tangent space at each point and equip it with an inner product called the Riemannian metric n Path length on the manifold is expressed as n Riemannian metric is coordinate free n Once a coordinate system is selected, it can be expressed using the first fundamental form coefficients n No more extrinsic geometry

Numerical geometry of non-rigid shapes Geometry 15 Nash’s embedding theorem n Seemingly, the intrinsic definition is more general n In 1956, Nash showed that any Riemannian metric can be realized as an embedded surface in a Euclidean space of sufficiently high but finite dimension n Nash’s embedding theorem implies that intrinsic and extrinsic views are equivalent

Numerical geometry of non-rigid shapes Geometry 16 Isometries n Two geometries and are indistinguishable, if there exists a mapping which is n Metric preserving: n Surjective: n Such a mapping is called an isometry n and are said to be isometric n is called a self-isometry

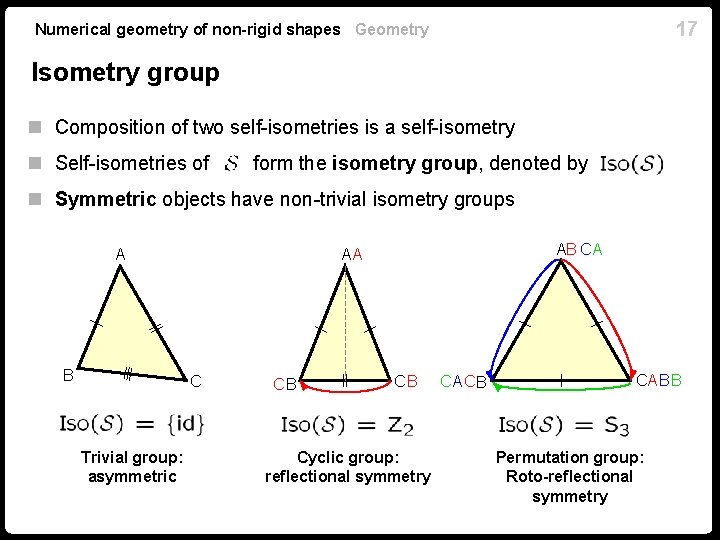
17 Numerical geometry of non-rigid shapes Geometry Isometry group n Composition of two self-isometries is a self-isometry n Self-isometries of form the isometry group, denoted by n Symmetric objects have non-trivial isometry groups A B C Trivial group: asymmetric AB C A AA CB CB Cyclic group: reflectional symmetry CACB CA B B Permutation group: Roto-reflectional symmetry

Numerical geometry of non-rigid shapes Geometry 18 Congruence n Isometry group of are translation, rotation and reflection transformations (congruences) n Congruences preserve the extrinsic geometry of an object n What are the transformations preserving the intrinsic geometry? n Extrinsic geometry fully defines intrinsic geometry n Hence, intrinsic geometry is invariant to congruences n Are there richer transformations? n Can a given intrinsic geometry have different incongruent realizations as an embedded surface?

Numerical geometry of non-rigid shapes Geometry Bending n Some objects have non-unique embedding into n Given two embeddings and of some intrinsic geometry n An isometry is called a bending n A bendable object may have different extrinsic geometries, while having the same intrinsic one 19

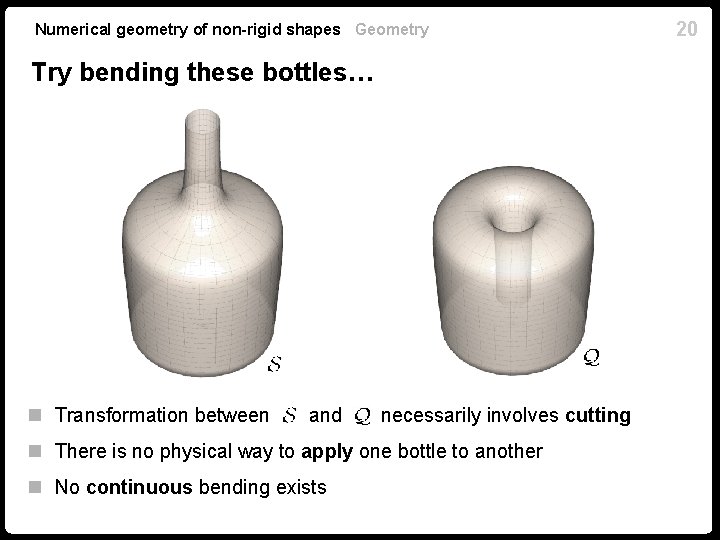
Numerical geometry of non-rigid shapes Geometry Try bending these bottles… n Transformation between and necessarily involves cutting n There is no physical way to apply one bottle to another n No continuous bending exists 20

Numerical geometry of non-rigid shapes Geometry Continuous bending n For some objects, there exists a continuous family of bendings such that n Object can be physically applied to without stretching or tearing n Such objects are called applicable or continuously bendable 21

Numerical geometry of non-rigid shapes Geometry 22 Rigidity n Objects that cannot be bent are rigid n Rigid objects have their extrinsic geometry completely defined (up to a congruence) by the intrinsic one n Rigidity interested mathematicians for centuries n 1766 Euler’s Rigidity Conjecture: every polyhedron is rigid n 1813 Cauchy proves that every convex polyhedron is rigid n 1927 Cohn-Vossen shows that all surfaces with positive Gaussian curvature are rigid n 1974 Gluck shows that almost all triangulated simply connected surfaces are rigid, remarking that “Euler was right statistically” n 1977 Connelly finally disproves Euler’s conjecture

Numerical geometry of non-rigid shapes Geometry 23 Rigidity n These results may give the impression that the world is more rigid than non-rigid n This is probably true, if isometry is considered in the strict sense n Many objects have some elasticity and therefore can bend n To account for this, the notion of isometry needs to be relaxed

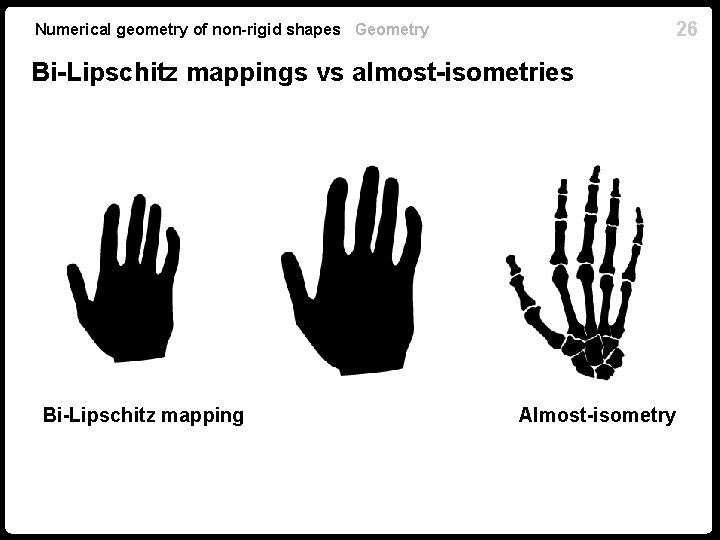
Numerical geometry of non-rigid shapes Geometry Bi-Lipschitz mappings n Relative distortion of the metric is bounded n Lipschitz constant is called the dilation of n Bi-Lipschitz mapping is bijective n Preserves topology n Absolute change in large distances is larger n Unsuitable to model objects with little elasticity 24

Numerical geometry of non-rigid shapes Geometry Almost-isometries n Absolute distortion of the metric is bounded n Map is almost surjective n On large scales behaves almost like an isometry n On small scales, may have arbitrarily bad behavior n May be discontinuous n Does not necessarily preserve topology n Suitable for modeling objects with no or little elasticity 25

26 Numerical geometry of non-rigid shapes Geometry Bi-Lipschitz mappings vs almost-isometries Bi-Lipschitz mapping Almost-isometry

Numerical geometry of non-rigid shapes Geometry 27 Curvature n Determines how the object is different from being flat n Measures how fast the normal vector rotates as we move on the surface n Positive curvature: normal rotates in the direction of the step n Negative curvature: normal rotates in the opposite direction n At each point, there usually exist two principal directions, corresponding to the largest and the smallest curvatures and n Mean curvature: n Gaussian curvature:

Numerical geometry of non-rigid shapes Geometry 28 Curvature n Gaussian curvature is defined as product of principal curvatures n Alternative definition: measure the perimeter of a small geodesic ball of radius on the surface n Up to the second order, the result will coincide with the Euclidean one n The third order term is controlled by the Gaussian curvature n Perimeter can be measured by a bug living on the surface and knowing nothing about the ambient space n Gaussian curvature is an intrinsic quantity!

Numerical geometry of non-rigid shapes Geometry 29 Theorema Egregium theorema: si superficies curva in quamcunque aliam superficiem explicatur, mensura curvaturae in singulis punctis invariata manet. Carl Friedrich Gauss (1777 -1855)

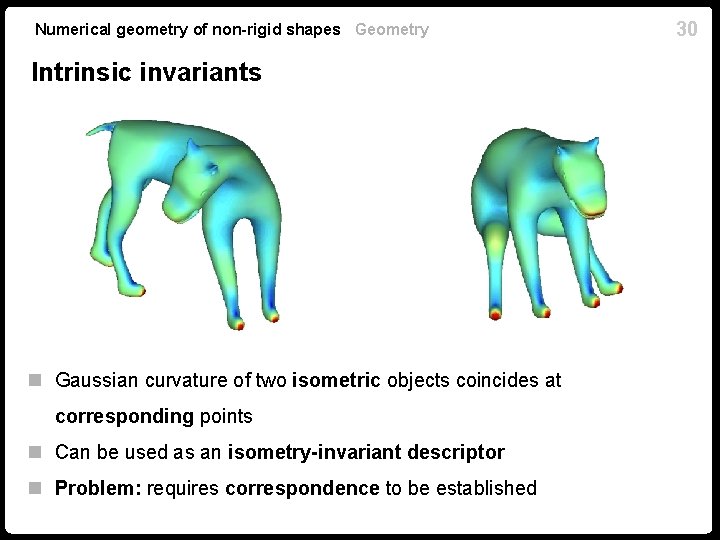
Numerical geometry of non-rigid shapes Geometry Intrinsic invariants n Gaussian curvature of two isometric objects coincides at corresponding points n Can be used as an isometry-invariant descriptor n Problem: requires correspondence to be established 30

Numerical geometry of non-rigid shapes Geometry Global invariants n Possible way around: integrate over the whole surface n Quantity known as the Euler characteristic n Still invariant to isometries n Topological rather than geometric n Too crude to recognize between objects 31

Numerical geometry of non-rigid shapes Geometry 32 Conclusions so far… n Non-rigid world can be modeled using almost-isometries n Extrinsic geometry is invariant to rigid deformations n Intrinsic geometry is invariant to isometric deformations n Comparison of non-rigid objects = comparison of intrinsic geometries n We need numerical tools to n compute intrinsic quantities n compare intrinsic quantities