Numerical geometry of nonrigid shapes Multidimensional scaling Alexander

Numerical geometry of non-rigid shapes Multidimensional scaling Alexander Bronstein, Michael Bronstein, Ron Kimmel © 2007 All rights reserved 1

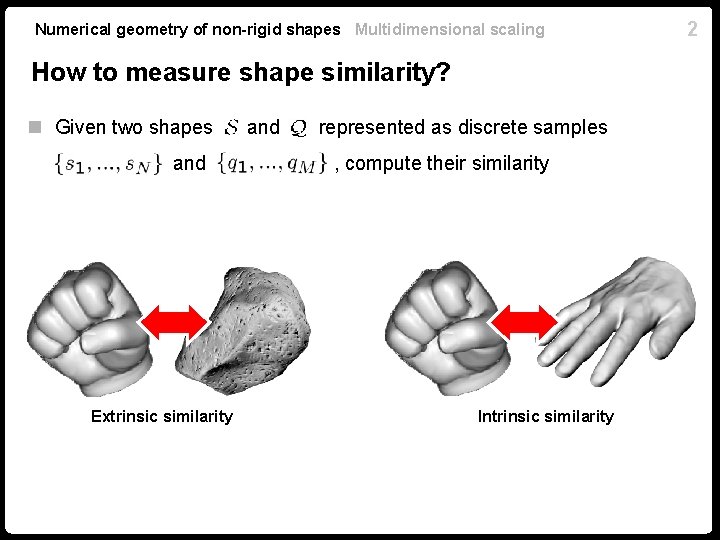
Numerical geometry of non-rigid shapes Multidimensional scaling How to measure shape similarity? n Given two shapes and Extrinsic similarity and represented as discrete samples , compute their similarity Intrinsic similarity 2

Numerical geometry of non-rigid shapes Multidimensional scaling 3 Rigid (extrinsic) similarity n Rigid shape similarity: congruence n Degrees of freedom: Euclidean transformations (rotation+translation) n Classical solution: iterative closest point (ICP) algorithm ROTATION MATRIX TRANSLATION VECTOR n Hausdorff distance as a measure of congruence between point clouds (other distances are usually preferred) Y. Chen, G. Medioni, 1991 P. J. Besl, N. D. Mc. Kay, 1992

Numerical geometry of non-rigid shapes Multidimensional scaling ICP in fairy tales Cinderella measuring the glass slipper Image: Disney 4

Numerical geometry of non-rigid shapes Multidimensional scaling 5 Non-rigid (intrinsic) similarity n Congruence is not a good criterion for similarity of non-rigid shapes n Geodesic distances are invariant to isometric deformations and can be easily computed using FMM n Naïve approach: directly compare matrices of geodesic distances n Problem: arbitrary ordering of points (permutation of rows and columns) n degrees of freedom

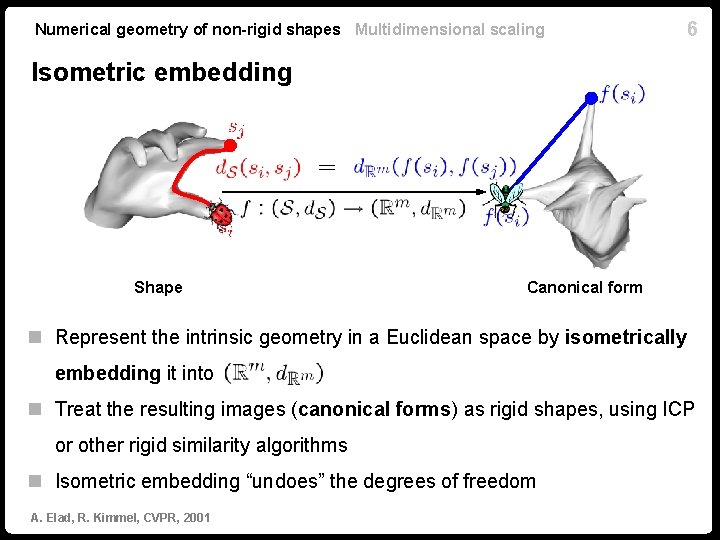
Numerical geometry of non-rigid shapes Multidimensional scaling 6 Isometric embedding Shape Canonical form n Represent the intrinsic geometry in a Euclidean space by isometrically embedding it into n Treat the resulting images (canonical forms) as rigid shapes, using ICP or other rigid similarity algorithms n Isometric embedding “undoes” the degrees of freedom A. Elad, R. Kimmel, CVPR, 2001

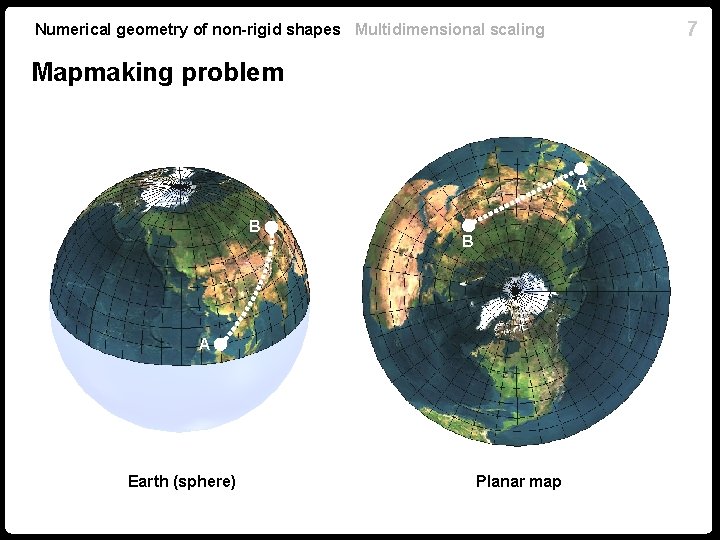
7 Numerical geometry of non-rigid shapes Multidimensional scaling Mapmaking problem A B B A Earth (sphere) Planar map

Numerical geometry of non-rigid shapes Multidimensional scaling Embedding error Theorema Egregium: a sphere has positive Gaussian curvature, the plane has zero Gaussian curvature, therefore, they are not isometric. n Every cartographer knows: impossible to create a distance-preserving planar map of the Earth! n Does isometric embedding into higher-dimensional spaces exist? 8

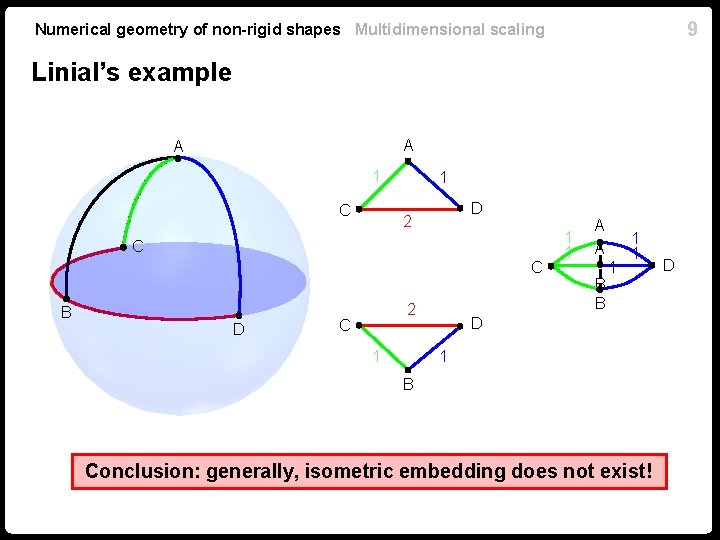
9 Numerical geometry of non-rigid shapes Multidimensional scaling Linial’s example A A 1 C 1 D 2 C C B D 2 C 1 1 1 A A B B 1 1 1 D 1 B Conclusion: generally, isometric embedding does not exist! D

Numerical geometry of non-rigid shapes Multidimensional scaling Minimum distortion embedding n Find an embedding that distorts the distances the least n Stress function is a measure of distortion where n Multidimensional scaling (MDS) problem 10

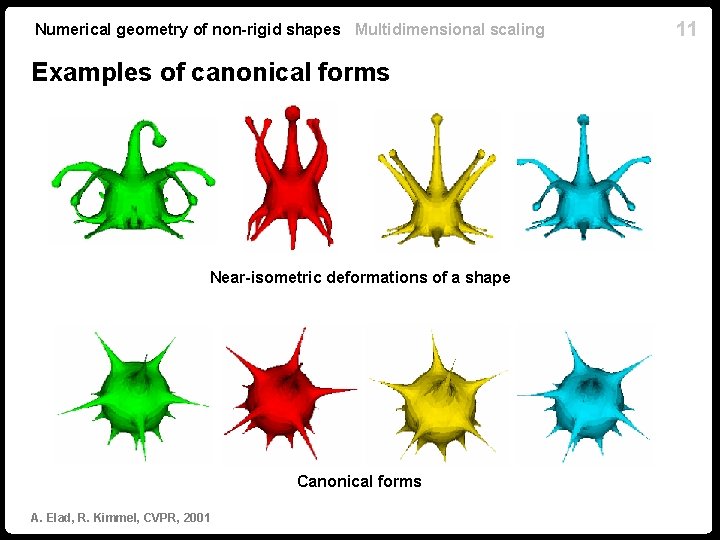
Numerical geometry of non-rigid shapes Multidimensional scaling Examples of canonical forms Near-isometric deformations of a shape Canonical forms A. Elad, R. Kimmel, CVPR, 2001 11

Numerical geometry of non-rigid shapes Multidimensional scaling Matrix expression of the L 2 -stress n - an matrix of coordinates in the embedding space n - an constant matrix with values n - an matrix-valued function 12

Numerical geometry of non-rigid shapes Multidimensional scaling MDS problem n variables n Non-convex non-linear optimization problem n Using convex optimization techniques is liable to local convergence n Optimum defined up to Euclidean transformation 13

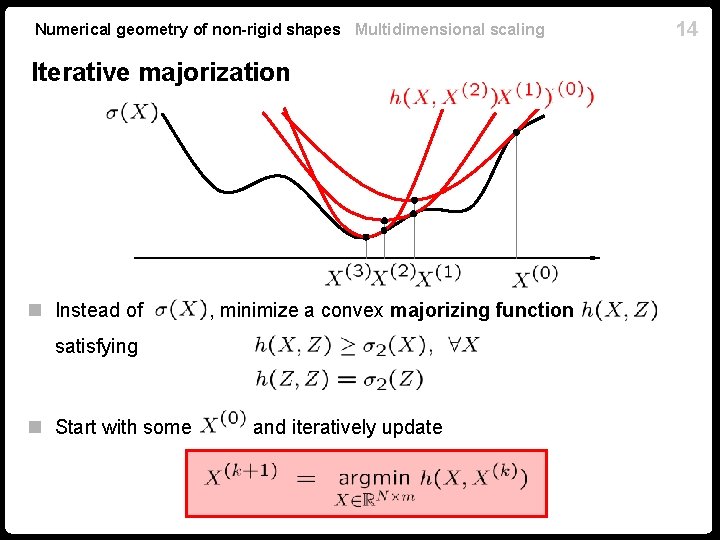
Numerical geometry of non-rigid shapes Multidimensional scaling Iterative majorization n Instead of , minimize a convex majorizing function satisfying n Start with some and iteratively update 14

Numerical geometry of non-rigid shapes Multidimensional scaling SMACOF algorithm n Majorize the stress by a convex quadratic function n Analytic expression for the minimum of : n SMACOF (Scaling by Minimizing a COnvex Function) 15

Numerical geometry of non-rigid shapes Multidimensional scaling SMACOF algorithm (cont) n Equivalent to constant-step gradient descent n Guarantees monotonically decreasing sequence of stress values n No guarantee of global convergence n Iteration cost: 16

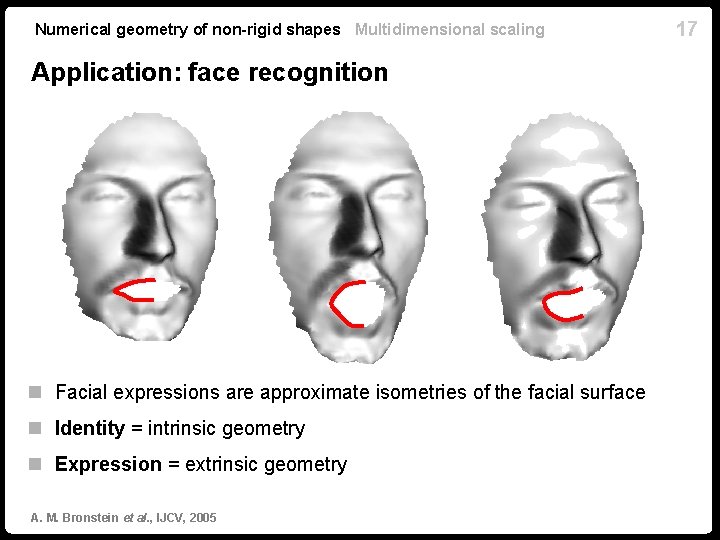
Numerical geometry of non-rigid shapes Multidimensional scaling Application: face recognition n Facial expressions are approximate isometries of the facial surface n Identity = intrinsic geometry n Expression = extrinsic geometry A. M. Bronstein et al. , IJCV, 2005 17

Numerical geometry of non-rigid shapes Multidimensional scaling 18 How to canonize a person? 3 D surface acquisition A. M. Bronstein et al. , IJCV, 2005 Cropping Smoothing Canonization

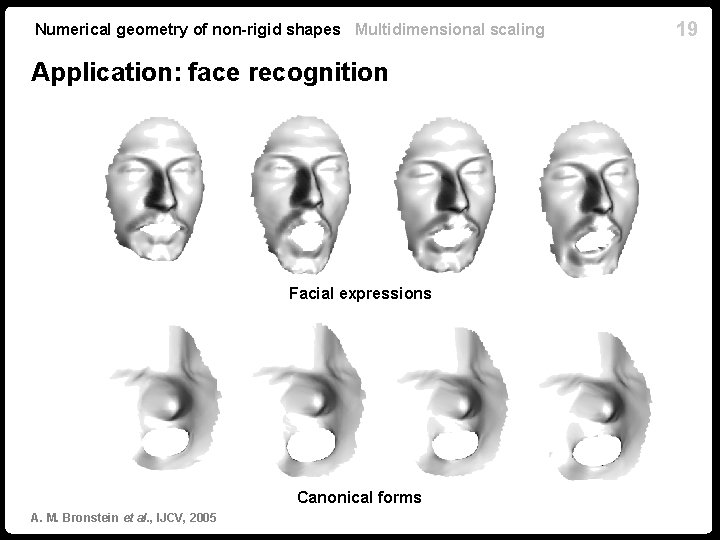
Numerical geometry of non-rigid shapes Multidimensional scaling Application: face recognition Facial expressions Canonical forms A. M. Bronstein et al. , IJCV, 2005 19

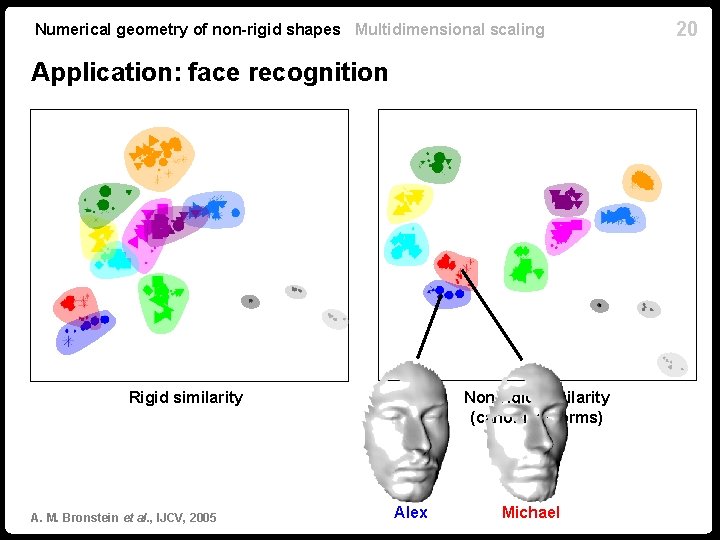
Numerical geometry of non-rigid shapes Multidimensional scaling Application: face recognition Rigid similarity A. M. Bronstein et al. , IJCV, 2005 Non-rigid similarity (canonical forms) Alex Michael 20

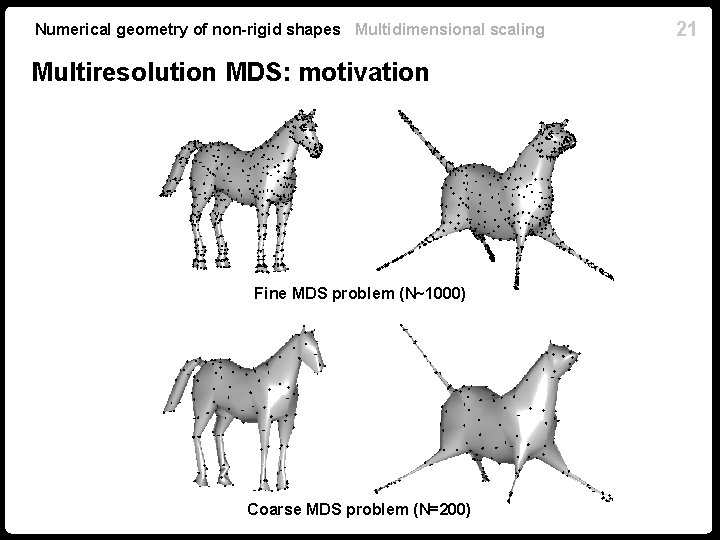
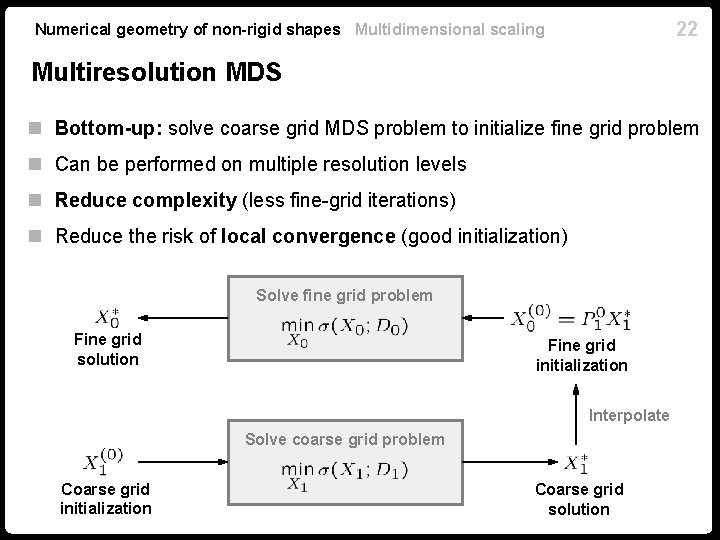
Numerical geometry of non-rigid shapes Multidimensional scaling Multiresolution MDS: motivation Fine MDS problem (N~1000) Coarse MDS problem (N=200) 21

22 Numerical geometry of non-rigid shapes Multidimensional scaling Multiresolution MDS n Bottom-up: solve coarse grid MDS problem to initialize fine grid problem n Can be performed on multiple resolution levels n Reduce complexity (less fine-grid iterations) n Reduce the risk of local convergence (good initialization) Solve fine grid problem Fine grid solution Fine grid initialization Interpolate Solve coarse grid problem Coarse grid initialization Coarse grid solution

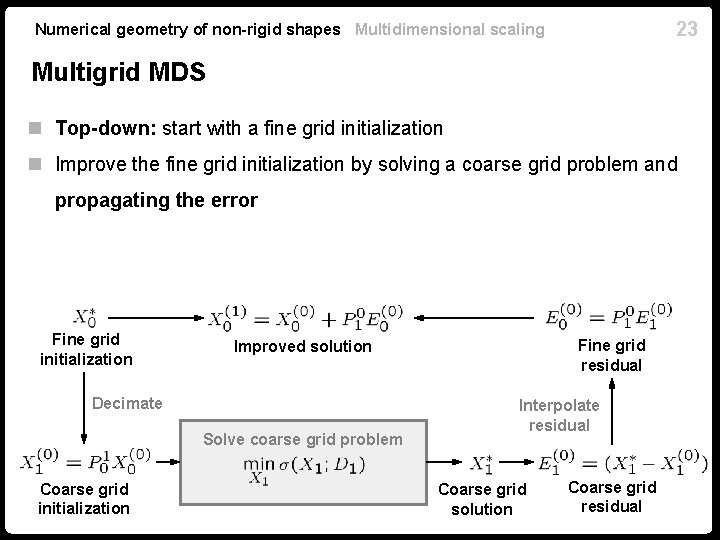
23 Numerical geometry of non-rigid shapes Multidimensional scaling Multigrid MDS n Top-down: start with a fine grid initialization n Improve the fine grid initialization by solving a coarse grid problem and propagating the error Fine grid initialization Decimate Solve coarse grid problem Coarse grid initialization Fine grid residual Improved solution Interpolate residual Coarse grid solution Coarse grid residual

Numerical geometry of non-rigid shapes Multidimensional scaling 24 Correction n Problem: the minima of fine and coarse grid problems do not coincide! n Add correction term to coarse grid problem to compensate for inconsistency CORRECTION n Choosing guarantees that M. M. Bronstein et al. , NLAA, 2006 is a coarse grid solution

Numerical geometry of non-rigid shapes Multidimensional scaling Modified stress n Another problem: the new coarse grid problem is unbounded! ( can be made arbitrarily large by adding a constant to without changing the stress) n Modified stress: add a quadratic penalty to the stress thus resolving translation ambiguity (forcing origin) M. M. Bronstein et al. , NLAA, 2006 to be centered at the 25

Numerical geometry of non-rigid shapes Multidimensional scaling Plugging everything together n Hierarchy of data n Interpolation and decimation operators to transfer variables and residuals from one resolution level to another n Hierarchy of optimization problems n Relaxation: optimization algorithm used to improve solution M. M. Bronstein et al. , NLAA, 2006 26

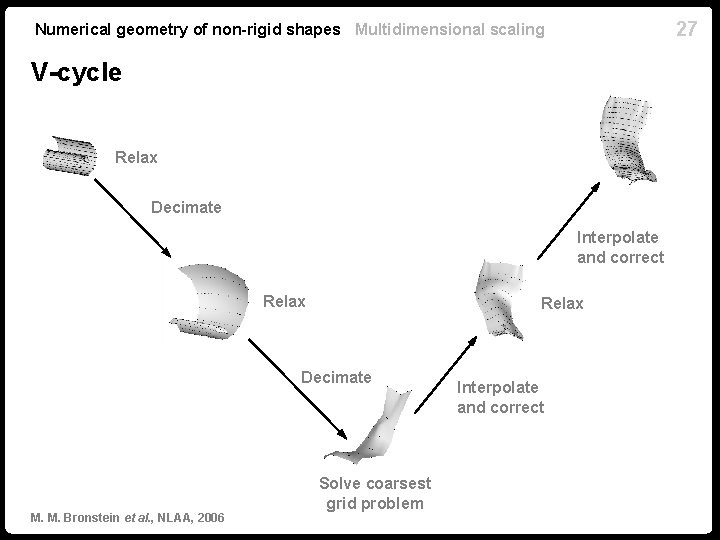
27 Numerical geometry of non-rigid shapes Multidimensional scaling V-cycle Relax Decimate Interpolate and correct Relax Decimate M. M. Bronstein et al. , NLAA, 2006 Solve coarsest grid problem Interpolate and correct

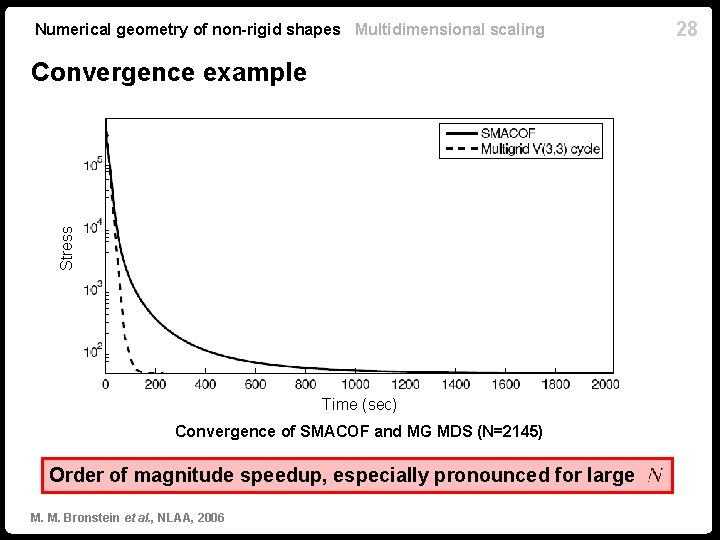
Numerical geometry of non-rigid shapes Multidimensional scaling Stress Convergence example Time (sec) Convergence of SMACOF and MG MDS (N=2145) Order of magnitude speedup, especially pronounced for large M. M. Bronstein et al. , NLAA, 2006 28

Numerical geometry of non-rigid shapes Multidimensional scaling How to choose the embedding space? n A generic, non-Euclidean embedding space n Must result in small embedding error (good representation) n Convenient representation of points in (local or preferably global parametrization) n Simple (preferably analytic) expression for distances n The isometry group is simple (few degrees of freedom) 29

Numerical geometry of non-rigid shapes Multidimensional scaling Possible choices n Schwartz et al. 1989: n Elad & Kimmel 2001: n Elad & Kimmel 2002: n BBK 2005: n Walter & Ritter 2002: Euclidean Spherical Hyperbolic Problem: embedding error can be reduced, but not made zero! 30

Numerical geometry of non-rigid shapes Multidimensional scaling Generalized MDS n Embedding space = triangular mesh n Generalized stress where is the image on triangular mesh n Generalized MDS (GMDS) problem A. M. Bronstein et al. , PNAS, 2006 31

Numerical geometry of non-rigid shapes Multidimensional scaling 32 Main differences n Difference 1: the distances have no analytic expression n Consequence 1: geodesic distance interpolation n Difference 2: points represented in local barycentric coordinates n Consequence 2: optimization with a modified line search (unfolding) A. M. Bronstein et al. , SIAM, 2006

33 Numerical geometry of non-rigid shapes Multidimensional scaling Distance interpolation n How to approximate the distances n Precompute the pair-wise distances between points ? between all mesh vertices using FMM n Find triangles and n Interpolate A. M. Bronstein et al. , SIAM, 2006 enclosing from known distances from

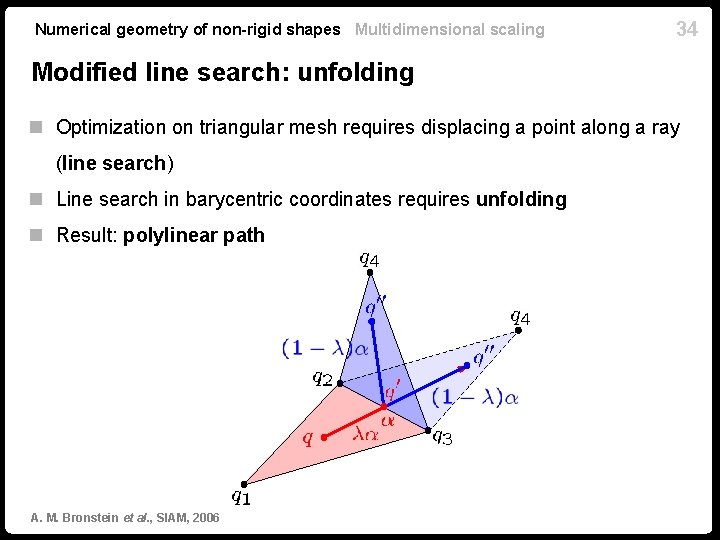
Numerical geometry of non-rigid shapes Multidimensional scaling 34 Modified line search: unfolding n Optimization on triangular mesh requires displacing a point along a ray (line search) n Line search in barycentric coordinates requires unfolding n Result: polylinear path A. M. Bronstein et al. , SIAM, 2006

Numerical geometry of non-rigid shapes Multidimensional scaling Conclusions so far n Geodesic distances are intrinsic descriptors of non-rigid shapes invariant to isometric deformations n MDS is an efficient method for representing and comparing intrinsic invariants n Multiresolution and multigrid methods can yield a significant convergence speedup and reduce the risk on local convergence n Generalized MDS allows avoiding the embedding error by embedding one surface into another 35