Multidimensional scaling Chapter 13 Statistics for Marketing Consumer

Multidimensional scaling Chapter 13 Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 1

Multidimensional scaling • a set of statistical techniques which allow one to 1. translate consumer preferences or perceptions towards products or brands into a reduced number of dimensions (usually two or three) 2. Represent them graphically into a preference map or perceptual map • It is also possible to show both objects and subjects (the consumers) in the same graph through multidimensional unfolding (MDU) • MDU is a technique which unfolds the coordinates for consumers (or groups of consumers) on the basis of their preferences or perceptions through an ideal point model Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 2

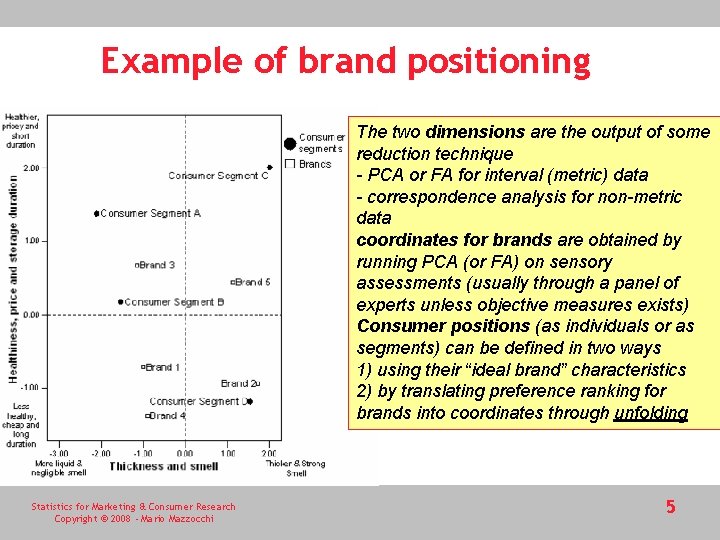
Interpretation: How trendy is the city Example of MDS output – holiday destinations in two dimensions May be interpreted as “climate” Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi • Each of the respondents is asked to rank the cities, without necessarily specifying why one city was preferred to another • Similarities in ranking across an adequate number of respondents reflect perceived similarities between cities (e. g. London is more similar to Berlin than to Athens) • Graph distances reflect dissimilarities • If the two dimensions can be labelled according to some criterion, as for principal component or factor analysis, then it becomes possible to understand the main perceived differences. 3

Marketing applications • Sensory evaluation and new product development • Example, a company developing a low-salt soup • An evaluation panel is asked to assess a set of existing soup brands according to several criteria concerning taste, smell, thickness, storage duration, perceived healthiness and price • Consumers are asked to identify their ideal product in terms of the same characteristics which may not coincide with one of the existing soups • The final output is a perceptual map displaying both consumer preferences (in terms of their ideal products) and the current positioning of the existing brand • A concentration of consumers’ ideal points identify a segment (cluster analysis might also be used as a tool to segment respondents) • if no brands appear in the neighbourhood of a segment then there is room for the development of a new product in that area • If the perceptual dimensions have been clearly identified this also allows one to choose the characteristics of the new products. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 4

Example of brand positioning The two dimensions are the output of some reduction technique - PCA or FA for interval (metric) data - correspondence analysis for non-metric data coordinates for brands are obtained by running PCA (or FA) on sensory assessments (usually through a panel of experts unless objective measures exists) Consumer positions (as individuals or as segments) can be defined in two ways 1) using their “ideal brand” characteristics 2) by translating preference ranking for brands into coordinates through unfolding Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 5

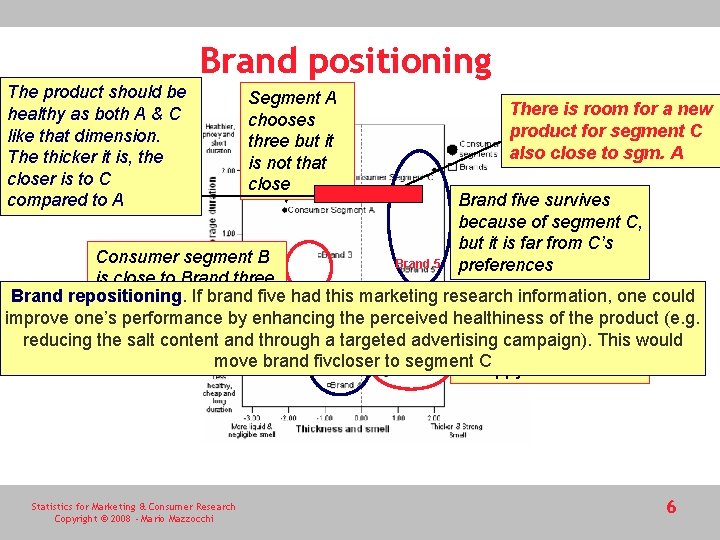
Brand positioning The product should be healthy as both A & C like that dimension. The thicker it is, the closer is to C compared to A Segment A chooses three but it is not that close There is room for a new product for segment C also close to sgm. A Brand five survives because of segment C, but it is far from C’s preferences Consumer segment B Brand 5 is close to Brand three Brand repositioning. If brand five had this marketing research information, one could improve one’s performance by enhancing the perceived healthiness of the product (e. g. 1 and 4 and arethrough a targeted advertising campaign). This would reducing the. Brand salt content Consumer segment D perceived asmove similar brand fivcloser to segment C is happy with Brand 2 Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 6

Other applications of MDS • If consumer perceptions are compared through MDS before and after an advertising campaign aimed at changing perceptions it becomes possible to measure the success of the advertising effort • Finally, MDS could be exploited to simplify data interpretation and provide some prior insight before running psycho-attitudinal surveys. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 7

Running MDS • MDS is a container for statistical techniques to produce perceptual or preference maps. • There is a range of options and choices depending on the type of MDS data. • object of the analysis: it can be a product, a brand or any other target of consumer behaviour, like tourism destinations in the initial example. The object can be depicted as a set of characteristics, represented through • objective dimensions (e. g. salt content in grams) • subjective dimensions as declared by respondents (subjects) in a survey Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 8

Preferences and perceptions • With subjective dimensions, consumer evaluations can be based on preferences or perceptions • Measurement through preferences (preference map) • the subjects rank several objects according their overall evaluations (e. g. ordering of soup brands). • Measurement through perceptions (perceptual or subjective dimensions, perceptual map) • the respondent must attach a subjective value to an object’s feature (e. g. a rating of the thickness of each soup brand) • When individual attribute perceptions are measured, respondents may be asked to state the combination of an object’s features that correspond to their ideal object (to be translated into an ideal point in the spatial map). • The ideal point can alternatively (and preferably) be derived through an unfolding statistical model. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 9

Measurement • Preferences • rank order scales • Q-sorting • other comparative scales. • Perceptions • non-comparative scales • Likert • Stapel • Semantic Differential Scales. • Two types of variables for MDS • Non-metric variables just reflect a ranking, so that it is not possible to assess whether the distance between the first and second object is larger or smaller than the distance between the second and the third. • Metric variables reflect respondent perception of the distances • Generally, preference rankings are classified as non-metric and perceptions and objective dimensions are metric. • This distinction can be very important, as it leads to two different MDS approaches. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 10

Non-metric vs. metric MDS • The output of non-metric MDS aims to preserve the preference ranking supplied by the respondents • Metric MDS also takes into account the distances as measured by perceptions or objective quantities. • This distinction is often overcome by the use of techniques which allow one to transform nonmetric variables and treat them as if they were metric, like the PRINQUAL procedure in SAS or correspondence analysis (see lecture 14) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 11

Multidimensional scaling steps 1. 2. 3. 4. 5. 6. 7. Decide whether mapping is based on an aggregate evaluation of the objects or on the evaluation of a set of attributes (decompositional versus compositional methods) Define the characteristics of the data collection step (number of objects, metric versus non-metric variables) Translate the survey or objective measurements into a similarity or preference data matrix Estimate the perceptual map Decide on the number of dimensions to be considered Label the dimensions and the ideal points Validate the analysis Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 12

Decompositional vs. compositional MDS • Decompositional (attribute-free) approach • The spatial maps reflect the subject evaluations • Comparisons of the objects in their integrity • Advantages: respondent assessment is easier, it is possible to obtain a separate perceptual map for each subject or for homogeneous groups of subjects • Limits: no specific information on the determinants of the relative position of the objects. It is not possible to plot both the objects and the subjects in the same map. It is difficult to label the dimensions (labels are based on the researcher’s knowledge about the objects) • Compositional (attributed-based) approach • Subject assess es a set of attributes (compositional or attribute-based approach). • Preferred when it is relevant to describe the dimensions and explain the positioning of objects and subjects in the perceptual map • Requirements: all the relevant attributes must be considered while avoiding including irrelevant ones; the combination of attributes must be adequate to reflect the overall object evaluation. • The method to be used depends on the chosen approach Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 13

Objects and variables • The higher the number of objects the more accurate the output of MDS in statistical terms • However, data quality suffers because it might be difficult for subjects to provide large number of comparisons. • The number of objects required for the analysis increases with the number of dimensions being considered • For two-dimensional MDS it is advisable to have at least ten objects • For three-dimensional MDS it is advisable to have about fifteen objects • As the number of objects increases goodness-of-fit measures become less reliable). • Measurement through metric or non-metric variables • The starting matrix for MDS is different • With non-metric data (ordinal variables or paired comparison data) the initial data matrix only considers ranking and not the distance between the objects • With metric variables the matrix preserves the distances observed in the subject evaluations. • Most of MDS methods can also deal with mixed data-set with both metric and non-metric data Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 14

Data matrix • Data for MDS are similarities between objects or preference (ranking) of objects • Decompositional approach: a matrix for each subject exists, which translates into a matrix comparing all objects • Compositional approach is chosen, a matrix for each subject and attribute exists and this translates into a matrix comparing all objects for each attribute • Similarity data: the subject compares all pairs of objects and ranks the pairs in terms of their similarity (usually this leads to non-metric MDS) • The similarity (or dissimilarity) matrix can be also computed from metric evaluation (rating) of the objects • Compositional approach: summarize (e. g. through averaging) the distances between the objects across the subjects, assuming all subjects have the same weight • Decompositional approach: a synthetic measure of similarity between objects is computed for each subject (weights can be used if available and appropriate) then the similarity matrix across the subjects is derived Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 15

Estimation • Estimation starts from a proximity or similarity matrix and produces a set of n-dimensional coordinates • Distances in this n-dimensional space reflect as closely as possible the distances recorded by the proximity matrix • Metric scaling is based on a proximity matrix derived from metric data • Non-metric scaling projects dissimilarities based on ranking (ordinal variables) preserving the order emerging from the subjects’ preferences • Non-metric scaling should also be applied to metric distances when the researcher suspects that collected data might be affected by relevant measurement errors (e. g. when respondents may encounter difficulties in stating their perceptions with precision while ordering can be regarded as more reliable) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 16

Metric scaling • With metric variables, one might apply FA (or PCA) to reduce the dimensions and obtain the scores which represent the coordinates. However, there is a difference • Coordinates obtained from PCA and FA are the best representation of the original data matrix in terms of variability • Metric scaling coordinates ensure that the distance between two points is as close as possible to the distance as measured in the proximity matrix • Classical Multi. Dimensional Scaling technique (CMDS) also known as principal coordinate analysis • Decompositional approach (unique similarity matrix comparing all objects) • The proximity or similarity matrix is obtained by applying the Euclidean distance on the data matrix (or other distance measures as those for cluster analysis). • The objective of CMDS is to extract a a n-dimensional configuration of points whose distances dij* are as close as possible to the original distances dij according to the following quadratic equation Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 17

Non-metric scaling • Ordinal variables (preference data) • coordinates are obtained through computational algorithms • Many procedures. The original method (Shepard-Kruskal) is as follows • • • given a number of dimensions n, the p objects are represented through an arbitrary initial set of coordinates a function S is defined to measure how distant the current set of coordinates is from the original ordering (monotonicity requirement) using an iterative computer numerical algorithm the values that minimize S are found • The procedure can be extended to include a search for the optimal number of dimensions n. • Other algorithms: • • • ALSCAL (SPSS & SAS) Algorithms in the MDS procedure in SAS INDSCAL Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 18

Goodness-of-fit and STRESS • The STRESS measure (STandardized REsiduals Sum of Squares) is a function of the original and derived distances to evaluate the goodness-of-fit of a MDS solution: • The smaller the stress function, the closer are the derived distances to the original ones Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 19

STRESS and number of dimensions • The STRESS value decreases as the number of dimensions increases • The number of dimensions can be evaluated through a scree diagram of STRESS against the number of dimensions (as for FA, PCA or cluster analysis) where the optimal number corresponds to an elbow • The preferred number of dimensions is usually two or three which allows for graphical examination • The search usually goes from one to five dimensions • Identification of the optimal number within the metric and non-metric iterative algorithm • An additional step evaluates the STRESS function • The algorithm stops when the addition of a further dimension does not reduce the STRESS value to a perceptible extent • With two dimensions a STRESS value below 0. 05 is generally considered to be satisfactory. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 20

Labelling dimensions • Interpretable dimensions (attaching a meaning to coordinates) enhance the use of MDS maps (e. g. new product development) • Interpretation may be difficult • Compositional approaches (or attribute ratings are otherwise available) allow for more objective methods based on the relative weight of each attribute (something similar to factor loadings) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 21

Ideal points • Objective: position ideal points (for each subject) and the actual brand evaluations (the objects) within the same map • Ideal point: set of coordinates which represents the stated optimal combination of attributes (under the compositional approach) • If no precise statement is made by the subject it is still possible to locate the ideal point • Indirect positioning of ideal points is based on a procedure which ensures that distances of the objects from a subject’s ideal point reflect the preference ordering as much as possible Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 22

Internal vs. external preference mapping • Internal Preference Mapping (IPM) • the proximity matrix for the objects is based on evaluations from consumers. The final map shows: • products as they are perceived by the consumers • consumers according to their preferences. • External data (i. e. objective measures or expert evaluations) can be used to interpret the dimensions but not to draw the map • External Preference Mapping (EPM) • the proximity matrix contains objective (analytic) measures of product characteristics (or evaluations from expert panels) • The maps contain information external to the set of consumers which provide their evaluation of the products • The final map shows • products as they are evaluated by the external source • consumers according to their preferences Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 23

Internal preference mapping • The ideal point (or vector) for each subject is estimated from the preference orderings through unfolding • Example • four brands (A, B, C and D) are evaluated. • Consumer one states a preference ordering as D, B, C and A, where D is the most preferred brand • Consumer two states the ordering C, B, D, A • The ideal point for Consumer one will be closer to D and far away from A, while for Consumer two the ideal point will probably be still far away from A but closer to C than to D. • The distance of the ideal point from the objects in the product space should reflect as much as possible the ordering of the consumer preferences Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 24

IPM and unfolding • The ideal product is not necessarily a precise point in the preference map but could be represented as a line (or an arrow) going from the least preferred objects towards the most preferred ones • Unfolding approach • Decompose all preference orderings for a given set of objects (products) so that the same products can be represented in a lower dimensional space • Once the products are positioned on the preference map it is possible to see where the subjects (consumers) are positioned • While the dimensions reflect some product characteristics that are the same for all consumers each consumer attaches a different weight to those dimensions • Consumers have different ideal points because they place a different weight on the dimensions Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 25

External preference mapping • EPM follows a different philosophy from IPM – It strictly requires the use of perceptual (metric) data – Evaluations of the product characteristics are on a measurement scale rather than their simple ordering – Measurements are usually based on analytic or objective evaluations or expert evaluations (external to the set of consumers which provide their product evaluation). • The input matrix contains the (quantitative) measurements of all attributes for each product. • A data reduction techniques (usually PCA) allows one to attach a set of coordinates (the principal component scores) to each of the products • The principal components define the dimensions of the map and can be interpreted (labelled) through the component loadings. • An algorithm (e. g. PREFMAP) allows one to elicit the position of subjects (consumers) in the map. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 26

IPM or EPM? • Both approaches can be applied to the same data set but they reflect different philosophies – a consumer very much likes red full-bodied wine and white sweet and sparkling wine – IPM: these two products share similar preferences and will be positioned next to each other – EPM: the product characteristics are very different they will look distant on the perceptual map. • The choice between IPM and EPM is mainly related to the choice of prioritizing either the preferences of the subjects (IPM) or the product characteristics (EPM). • When many dimensions are chosen the two approaches produce similar results but with reduced dimensions discrepancies are likely to emerge Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 27

IPM vs. EPM • IPM is better when • Perceptual data are inadequate to reflect preferences as it is not necessarily true that the combination of the product attributes is an adequate representation for the product • Physical attributes as they are perceived by the consumer are processed into a number of perceived benefits and these benefits are then translated into preferences • Thus the relative weight of the physical attributes as compared to the abstraction process could drive the choice between IPM and EPM. • For those goods where the cognitive evaluation is mainly based on the objective attributes EPM seems to be preferable • Goods where the connection between perceptions and preferences is not so natural (and affective processes play a major role) are better analyzed with IPM Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 28

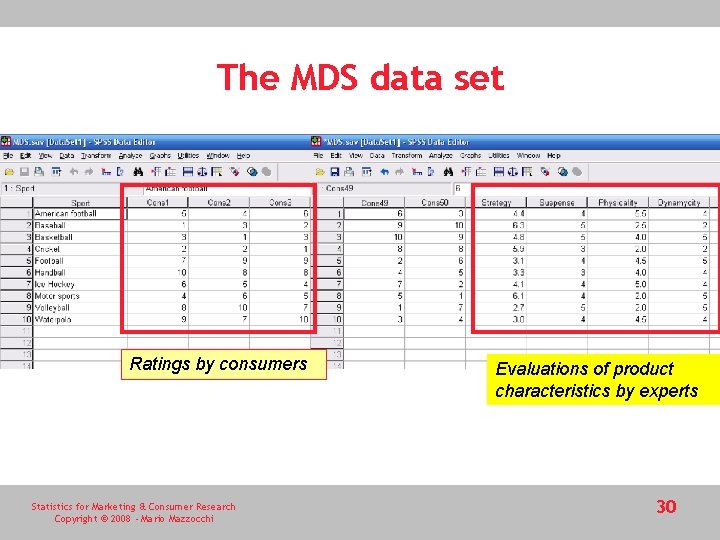
MDS in SPSS – the data • MDS data set • Fifty individuals (the subjects or consumers) were asked to rank ten sports (the objects or products) according to their preference • a panel of expert sport journalists provided an evaluation of the attributes of each sport (the product characteristics) in terms of strategy, suspense, physicality and dynamicity • The final data set (MDS. sav) has one row for each sport and one column for each consumer plus four columns for the sports’ attributes Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 29

The MDS data set Ratings by consumers Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi Evaluations of product characteristics by experts 30

IPM & unfolding Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 31

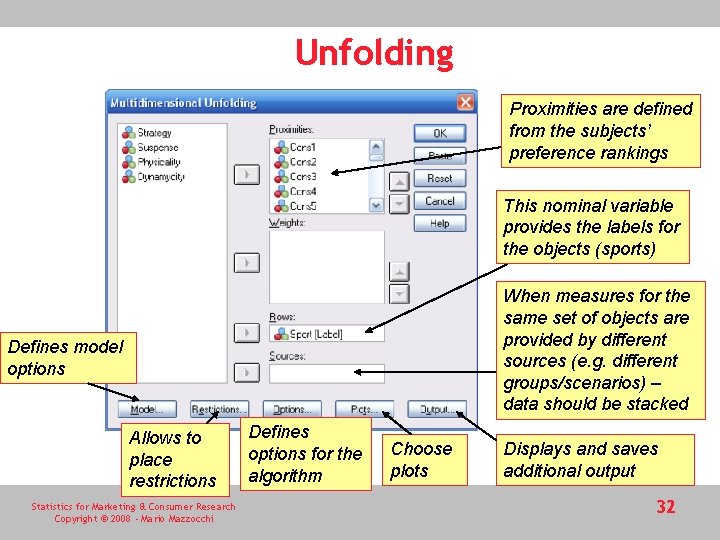
Unfolding Proximities are defined from the subjects’ preference rankings This nominal variable provides the labels for the objects (sports) When measures for the same set of objects are provided by different sources (e. g. different groups/scenarios) – data should be stacked Defines model options Allows to place restrictions Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi Defines options for the algorithm Choose plots Displays and saves additional output 32

Unfolding options Select identity as data come from a single source Rankings are dissimilarities and ordinal data Number of dimensions to be explored Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 33

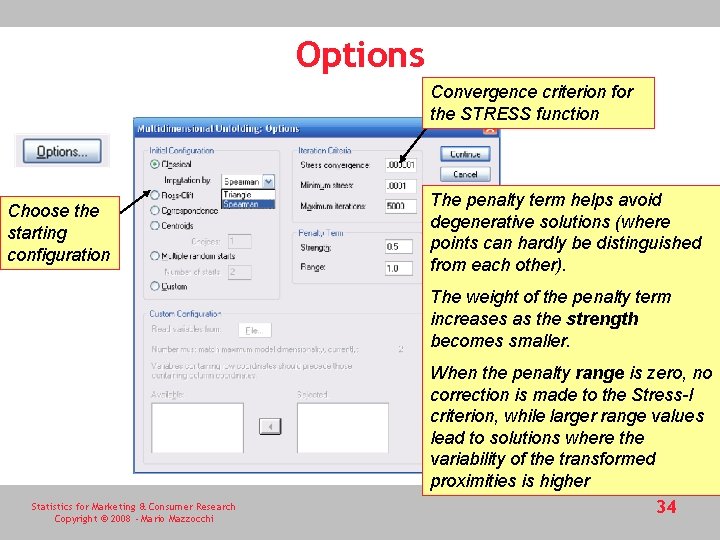
Options Convergence criterion for the STRESS function Choose the starting configuration The penalty term helps avoid degenerative solutions (where points can hardly be distinguished from each other). The weight of the penalty term increases as the strength becomes smaller. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi When the penalty range is zero, no correction is made to the Stress-I criterion, while larger range values lead to solutions where the variability of the transformed proximities is higher 34

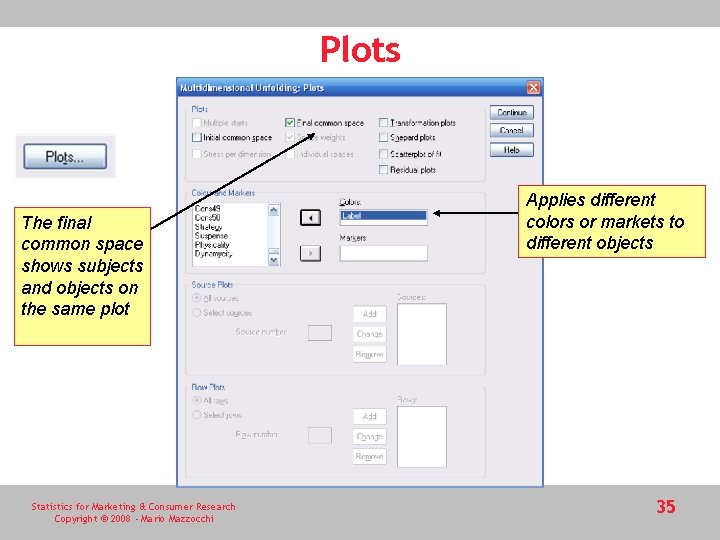
Plots The final common space shows subjects and objects on the same plot Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi Applies different colors or markets to different objects 35

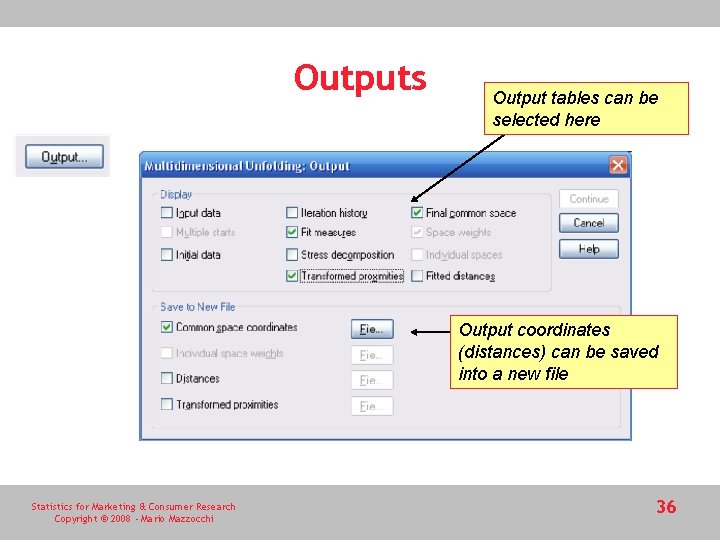
Outputs Output tables can be selected here Output coordinates (distances) can be saved into a new file Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 36

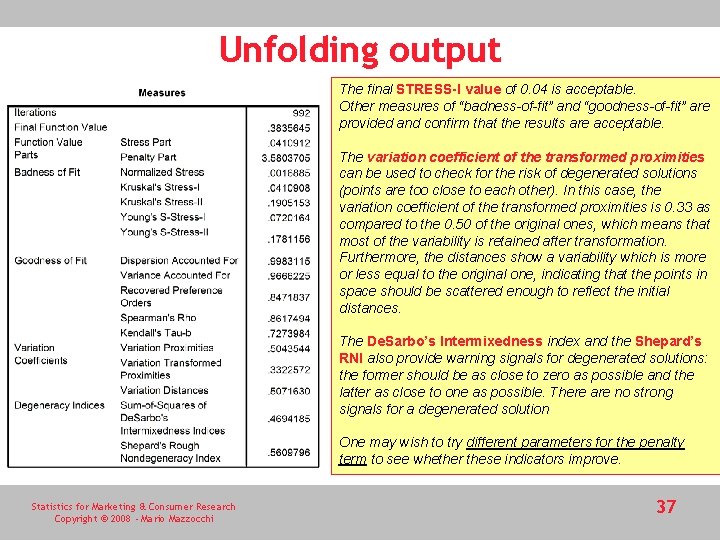
Unfolding output The final STRESS-I value of 0. 04 is acceptable. Other measures of “badness-of-fit” and “goodness-of-fit” are provided and confirm that the results are acceptable. The variation coefficient of the transformed proximities can be used to check for the risk of degenerated solutions (points are too close to each other). In this case, the variation coefficient of the transformed proximities is 0. 33 as compared to the 0. 50 of the original ones, which means that most of the variability is retained after transformation. Furthermore, the distances show a variability which is more or less equal to the original one, indicating that the points in space should be scattered enough to reflect the initial distances. The De. Sarbo’s Intermixedness index and the Shepard’s RNI also provide warning signals for degenerated solutions: the former should be as close to zero as possible and the latter as close to one as possible. There are no strong signals for a degenerated solution One may wish to try different parameters for the penalty term to see whether these indicators improve. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 37

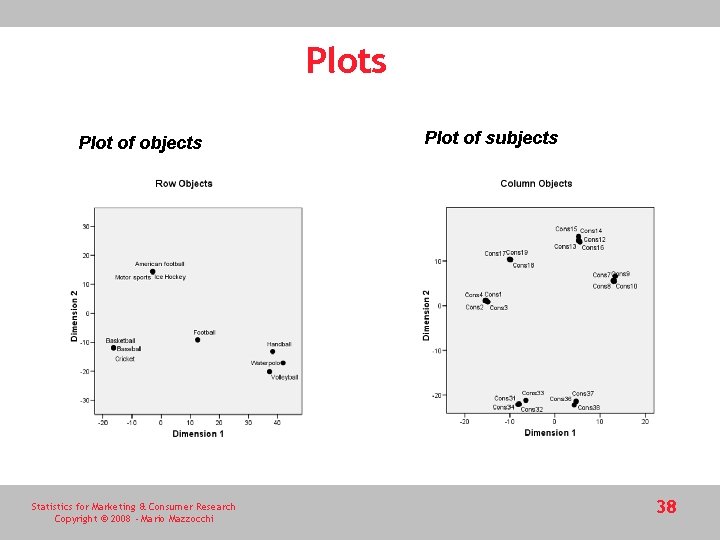
Plots Plot of objects Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi Plot of subjects 38

Joint plot According to the sample, basketball, baseball and cricket share similarities in subjects’ perceptions and so do American football, motor sports and ice hockey. A third “cluster” is provided by handball, waterpolo and volleyball, while football seems to be equidistant from all other sports. Consumers are also grouped in clusters according to their preferences and the joint representation allows one to show not only which sports (products) are closer to the preferences of different segments, but also which sports need to be repositioned to attract more public, like the cluster with volleyball, waterpolo and handball. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 39

Repositioning • If one can attach a meaning to dimensions one and two it becomes possible to understand what characteristics of the products should be changed • A method to obtain an interpretation of the coordinates consists in looking at the correlations betweens the coordinates of the sports and the object characteristics that can be measured objectively or through the evaluation of expert panellists. • The algorithm has created an output file coord. sav which contains the two coordinates for each sport and consumer and can be used to obtain the bivariate correlations Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 40

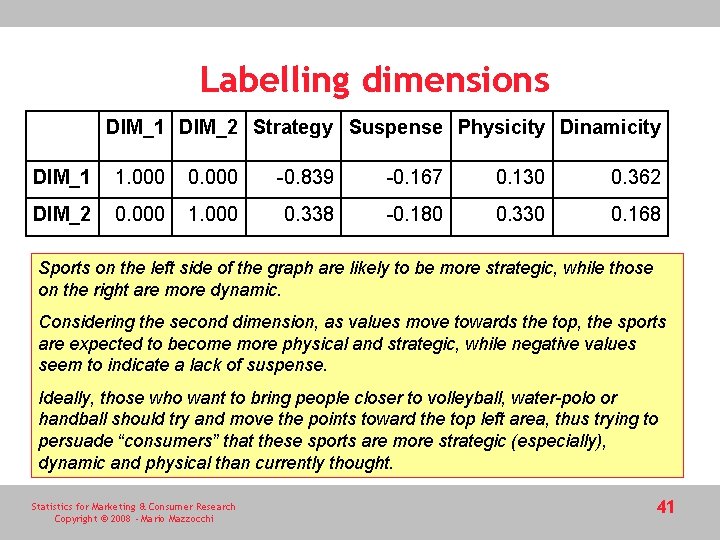
Labelling dimensions DIM_1 DIM_2 Strategy Suspense Physicity Dinamicity DIM_1 1. 000 0. 000 -0. 839 -0. 167 0. 130 0. 362 DIM_2 0. 000 1. 000 0. 338 -0. 180 0. 330 0. 168 Sports on the left side of the graph are likely to be more strategic, while those on the right are more dynamic. Considering the second dimension, as values move towards the top, the sports are expected to become more physical and strategic, while negative values seem to indicate a lack of suspense. Ideally, those who want to bring people closer to volleyball, water-polo or handball should try and move the points toward the top left area, thus trying to persuade “consumers” that these sports are more strategic (especially), dynamic and physical than currently thought. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 41

SAS procedures • The SAS procedure for multidimensional scaling (proc MDS) is a generalization of the ALSCAL algorithm • MDS applies multidimensional scaling as a mapping technique for objects, but does not perform unfolding • The TRANSREG procedure allows unfolding • There is an option (COO) which returns the coordinates of the ideal point or vector for internal preference mapping • proc PRINQUAL performs PCA on qualitative data Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 42