Variations of the Turing Machine part 2 1

Variations of the Turing Machine part 2 1

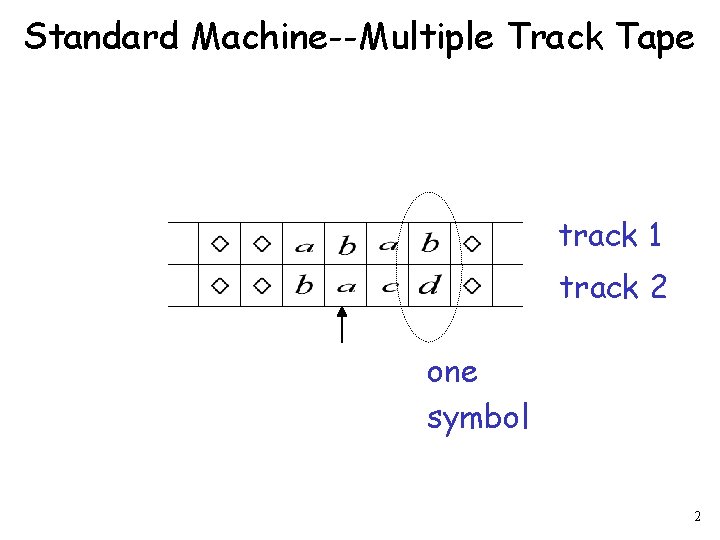
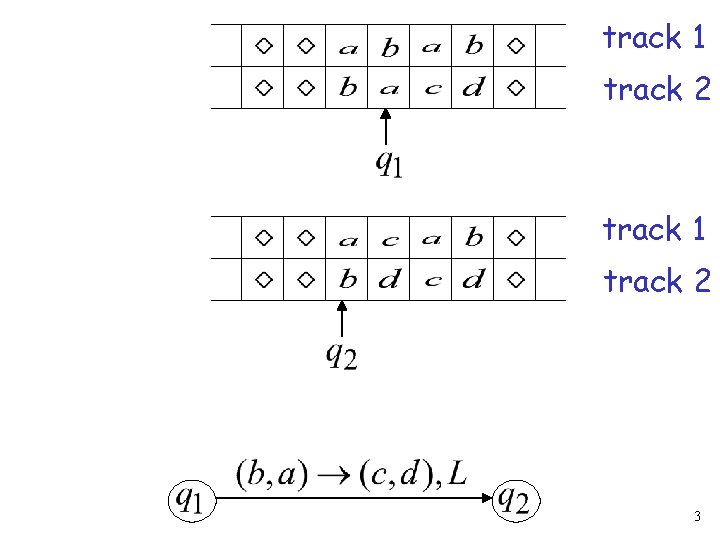
Standard Machine--Multiple Track Tape track 1 track 2 one symbol 2

track 1 track 2 3

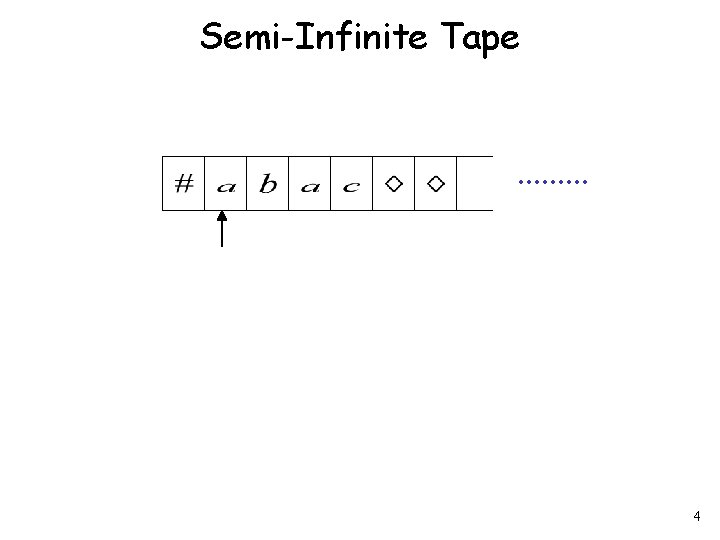
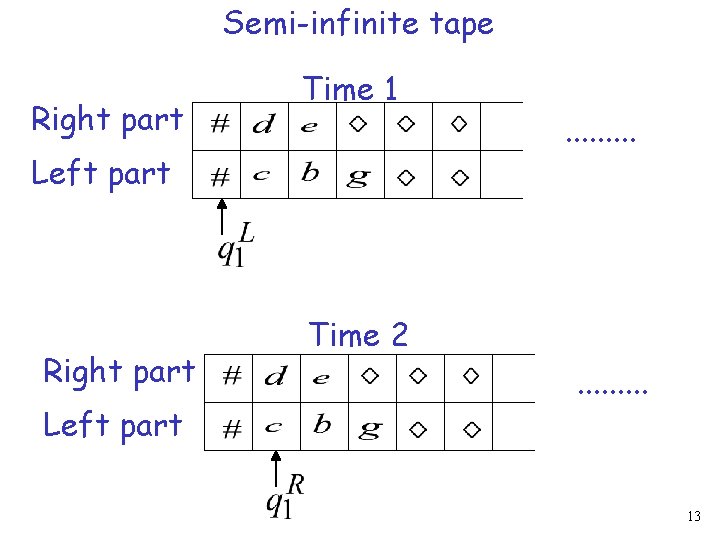
Semi-Infinite Tape. . 4

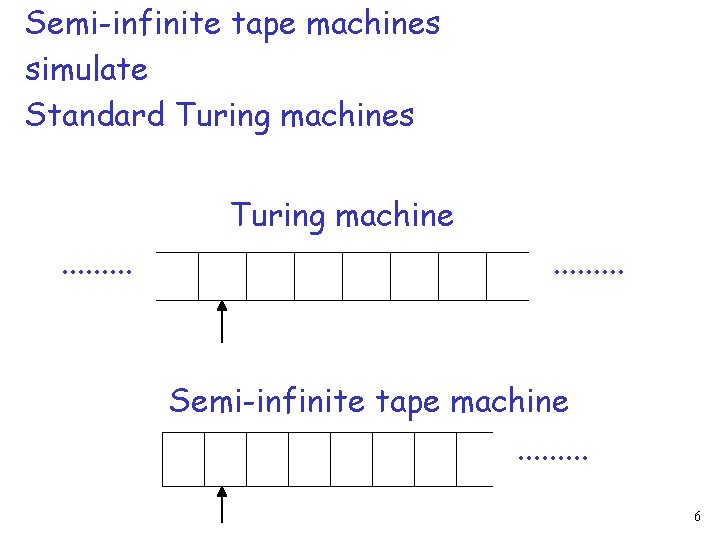
Standard Turing machines simulate Semi-infinite tape machines Trivial 5

Semi-infinite tape machines simulate Standard Turing machines Turing machine. . . . Semi-infinite tape machine. . 6

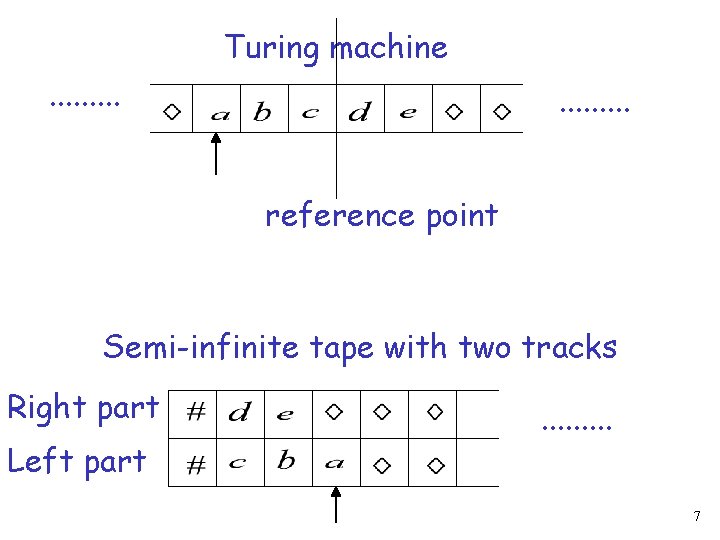
Turing machine. . . . reference point Semi-infinite tape with two tracks Right part Left part . . 7

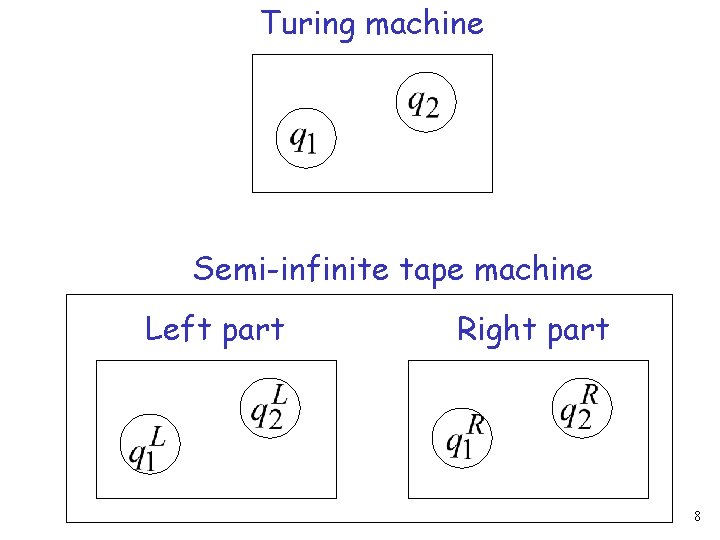
Turing machine Semi-infinite tape machine Left part Right part 8

Turing machine Semi-infinite tape machine Right part Left part For all symbols x 9

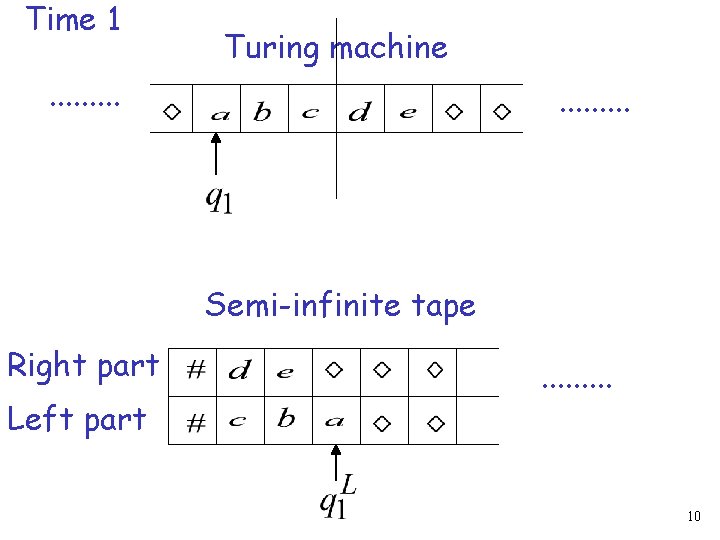
Time 1 Turing machine . . . . Semi-infinite tape Right part Left part . . 10

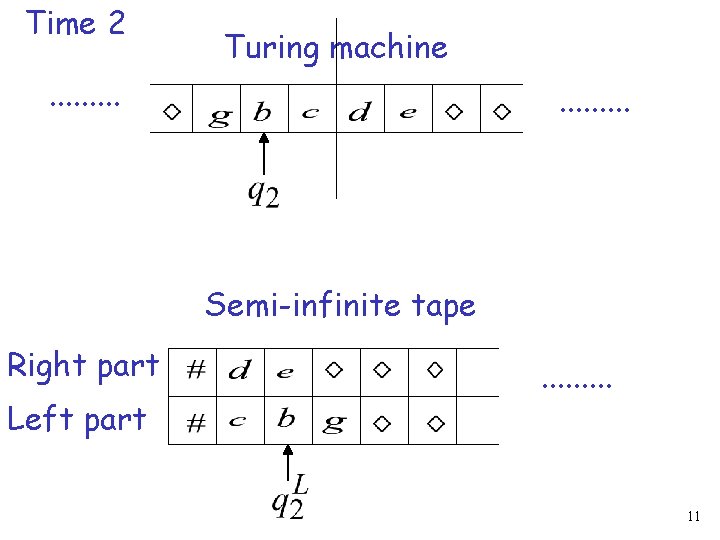
Time 2 Turing machine . . . . Semi-infinite tape Right part Left part . . 11

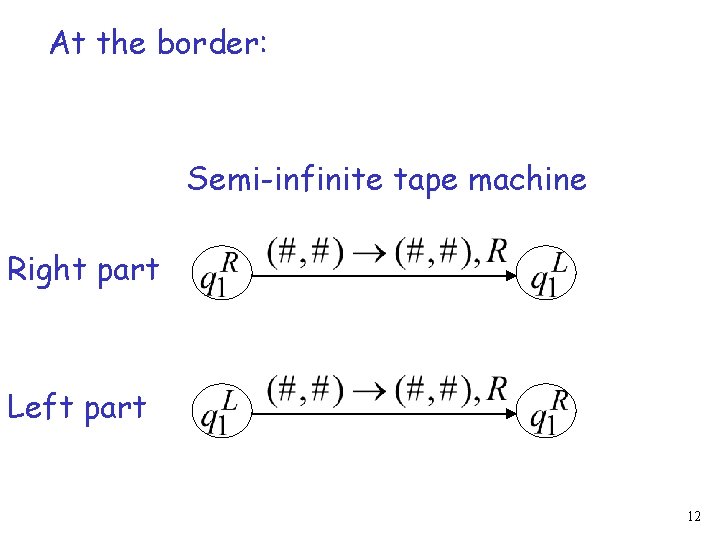
At the border: Semi-infinite tape machine Right part Left part 12

Semi-infinite tape Right part Time 1 Left part Right part Left part . . Time 2. . 13

Theorem: Semi-infinite tape machines have the same power with Standard Turing machines 14

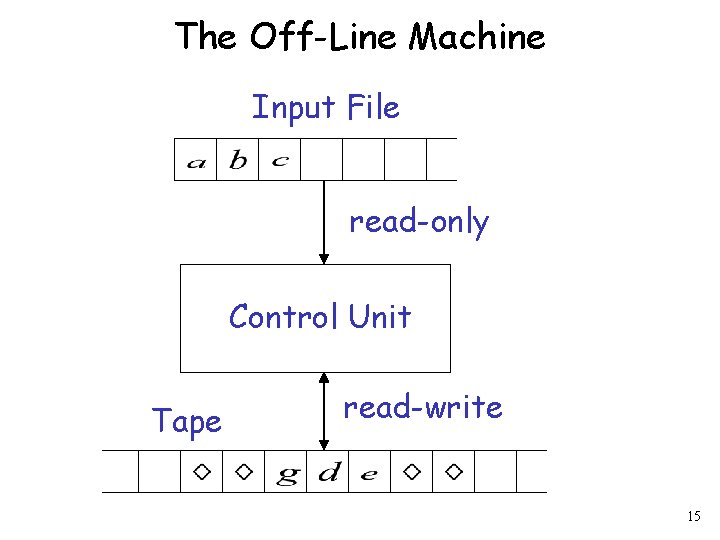
The Off-Line Machine Input File read-only Control Unit Tape read-write 15

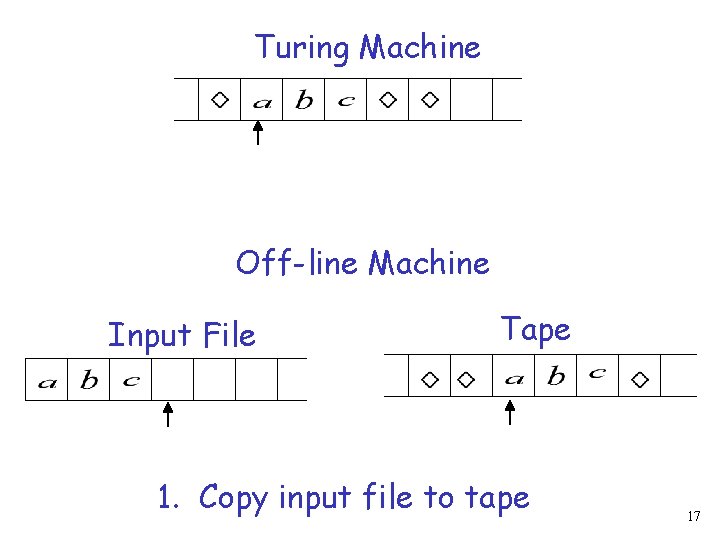
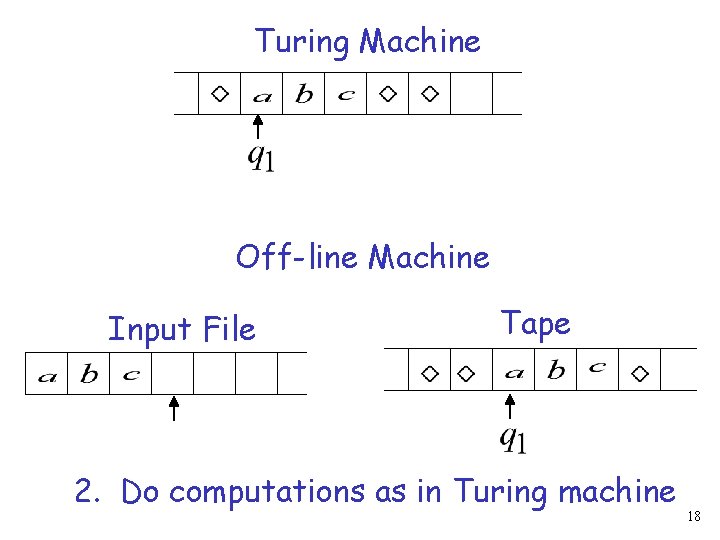
Off-line Machines simulate Turing Machines Off-line machine: 1. Copy input file to tape 2. Continue computation as in Standard Turing machine 16

Turing Machine Off-line Machine Input File Tape 1. Copy input file to tape 17

Turing Machine Off-line Machine Input File Tape 2. Do computations as in Turing machine 18

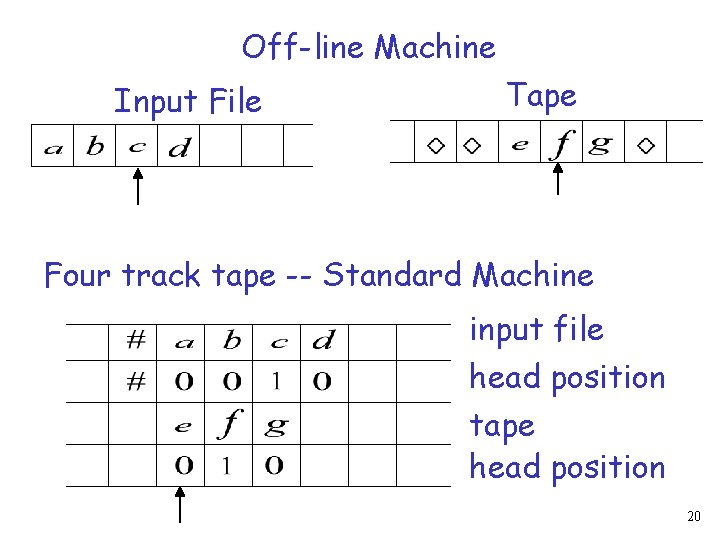
Turing Machines simulate Off-line machines Use a Standard machine with four track tape to keep track of the Off-line input file and tape contents 19

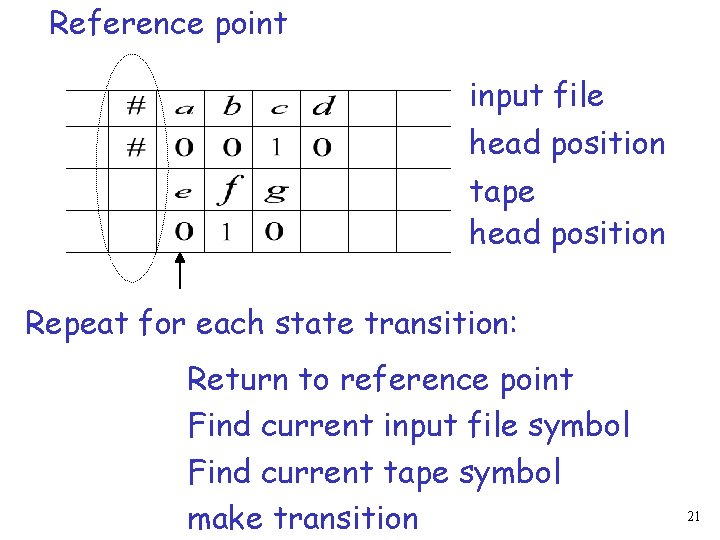
Off-line Machine Input File Tape Four track tape -- Standard Machine input file head position tape head position 20

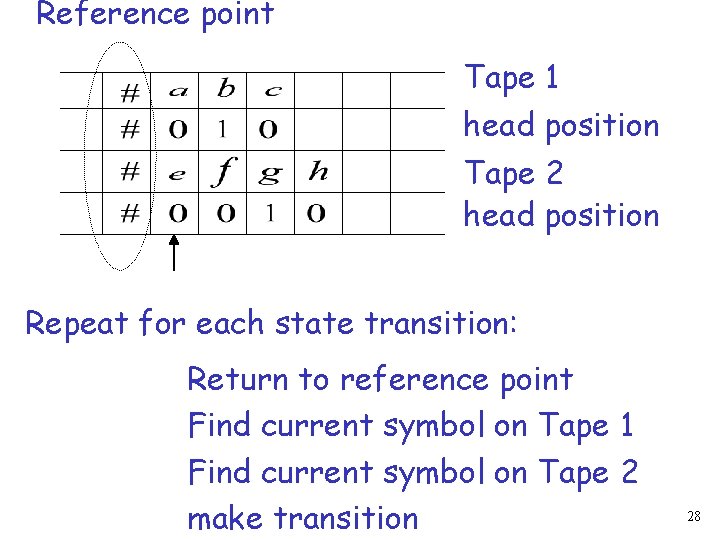
Reference point input file head position tape head position Repeat for each state transition: Return to reference point Find current input file symbol Find current tape symbol make transition 21

Theorem: Off-line machines have the same power with Stansard machines 22

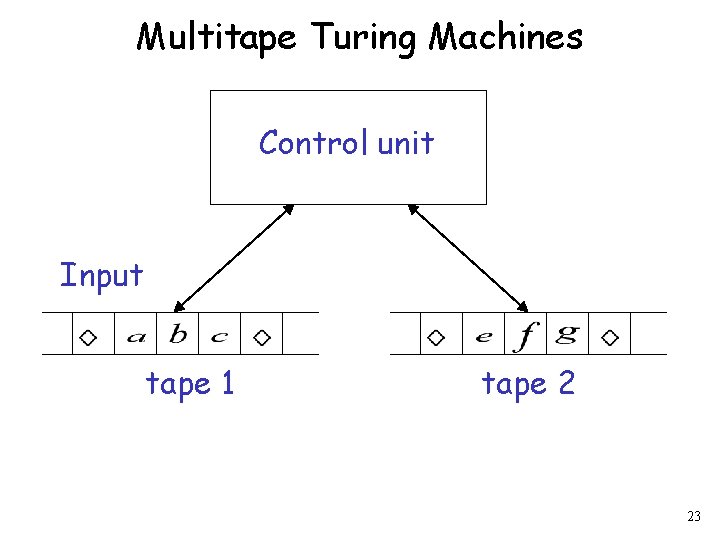
Multitape Turing Machines Control unit Input tape 1 tape 2 23

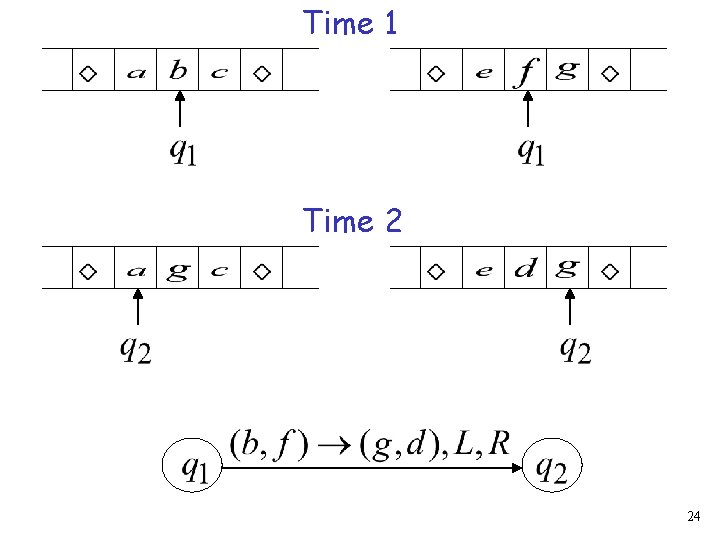
Time 1 Time 2 24

Multitape machines simulate Standard Machines Just use one tape 25

Standard machines simulate Multitape machines Standard machine: Use a multi-track tape A tape of the Multiple tape machine corresponds to a pair of tracks 26

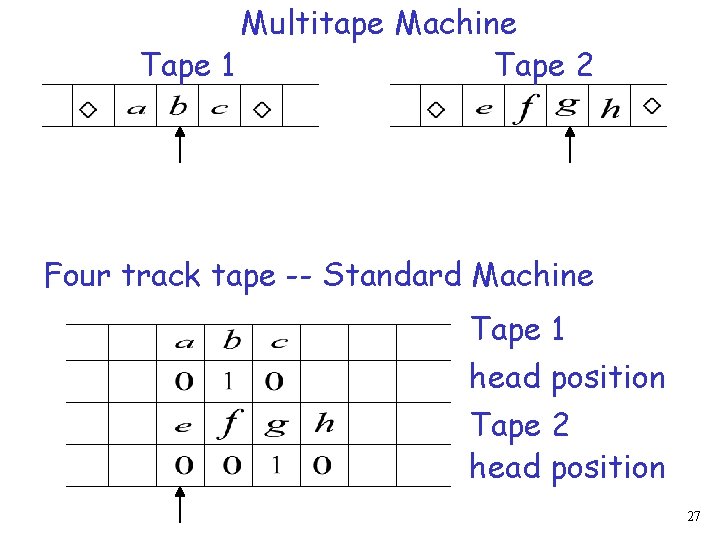
Multitape Machine Tape 1 Tape 2 Four track tape -- Standard Machine Tape 1 head position Tape 2 head position 27

Reference point Tape 1 head position Tape 2 head position Repeat for each state transition: Return to reference point Find current symbol on Tape 1 Find current symbol on Tape 2 make transition 28

Theorem: Multi-tape machines have the same power with Standard Turing Machines 29

Same power doesn’t mean same speed: Language Acceptance Time Standard machine Two-tape machine 30

Standard machine: Go back and forth times Two-tape machine: Copy Leave to tape 2 ( steps) to tape 1 ( steps) Compare tape 1 and tape 2 31

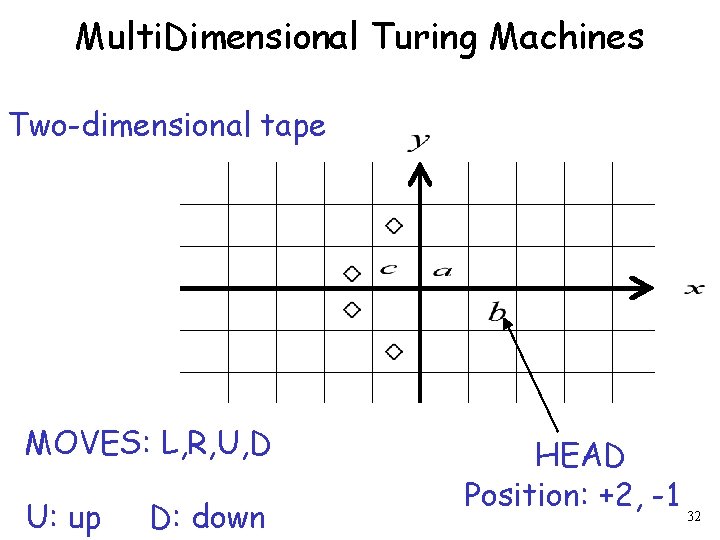
Multi. Dimensional Turing Machines Two-dimensional tape MOVES: L, R, U, D U: up D: down HEAD Position: +2, -1 32

Multidimensional machines simulate Standard machines Just use one dimension 33

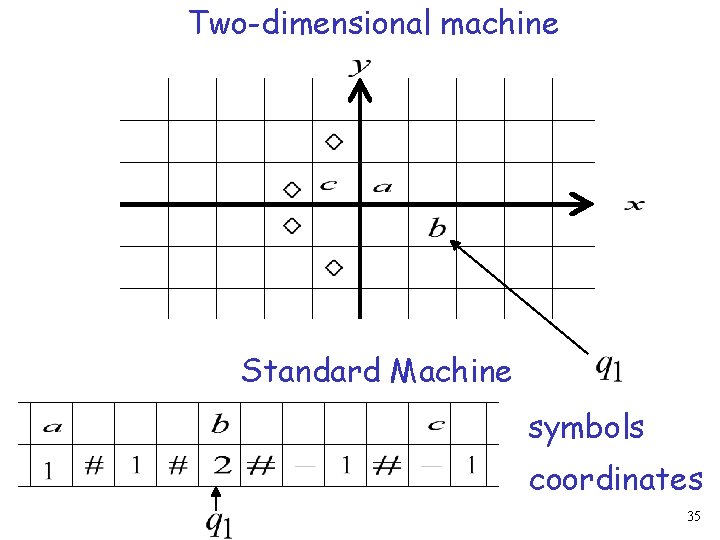
Standard machines simulate Multidimensional machines Standard machine: Use a two track tape Store symbols in track 1 Store coordinates in track 2 34

Two-dimensional machine Standard Machine symbols coordinates 35

Simulation: Repeat for each transition Update current symbol Compute coordinates of next position Go to new position 36

Theorem: Multi. Dimensional Machines have the same power with Turing Machines 37

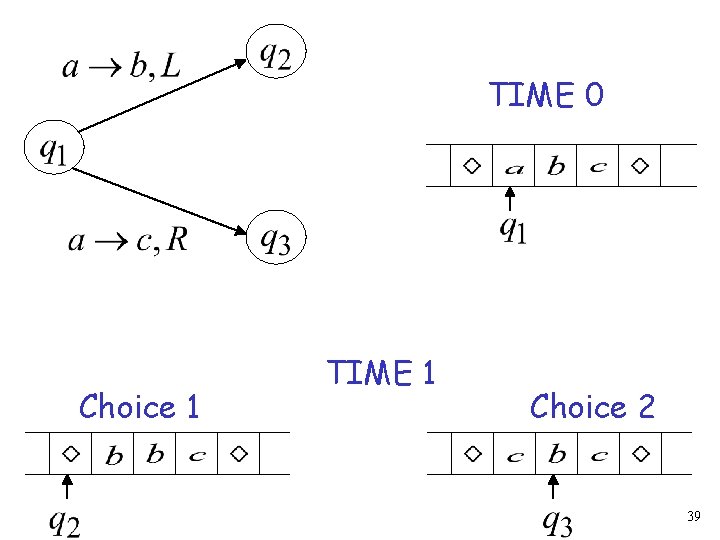
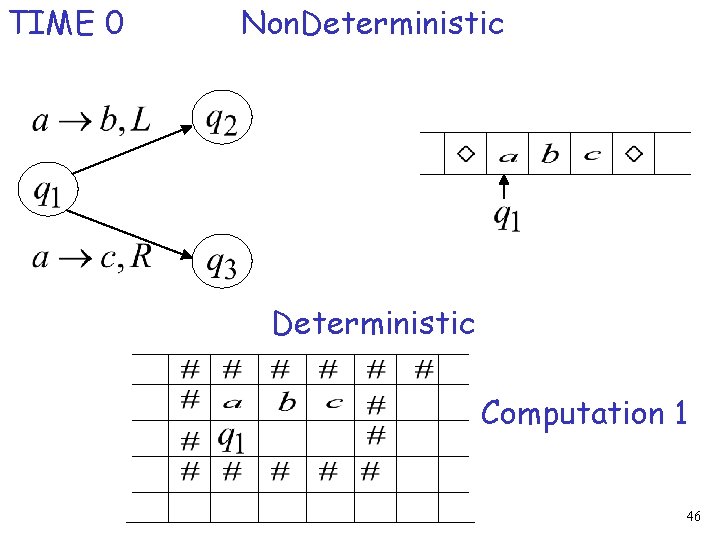
Non. Deterministic Turing Machines Non Deterministic Choice 38

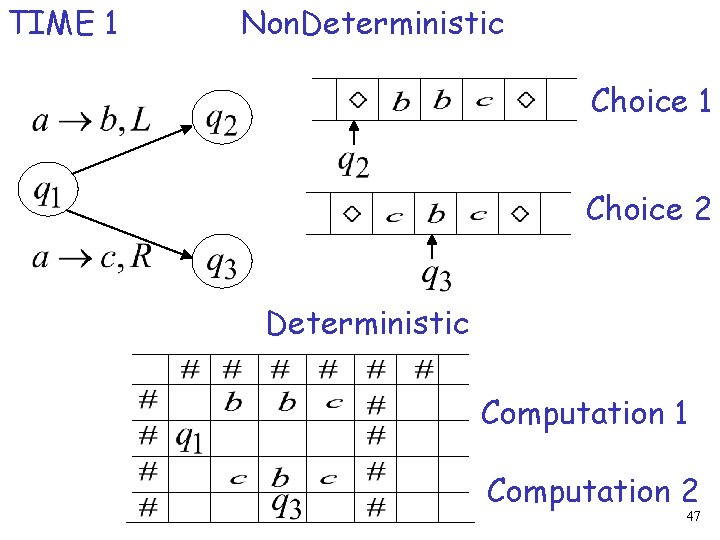
TIME 0 Choice 1 TIME 1 Choice 2 39

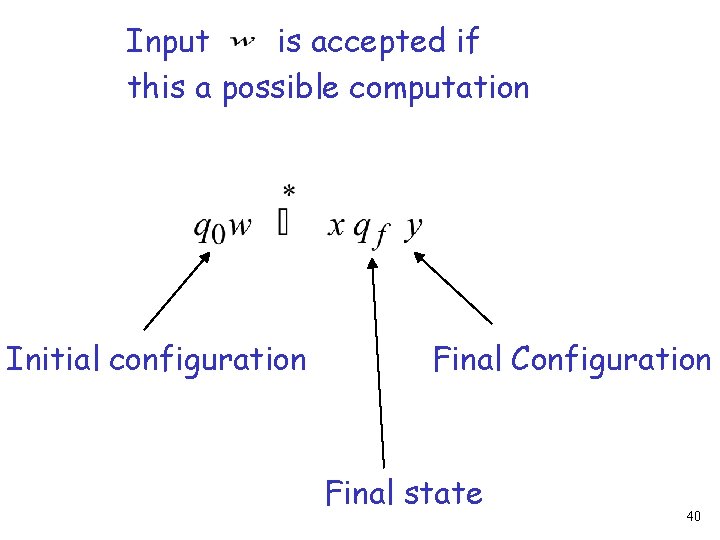
Input is accepted if this a possible computation Initial configuration Final Configuration Final state 40

Non. Deterministic Machines simulate Standard (deterministic) Machines Every deterministic machine is also a nondeterministic machine 41

Deterministic machines simulate Non. Deterministic machines Deterministic machine: Keeps track of all possible computations 42

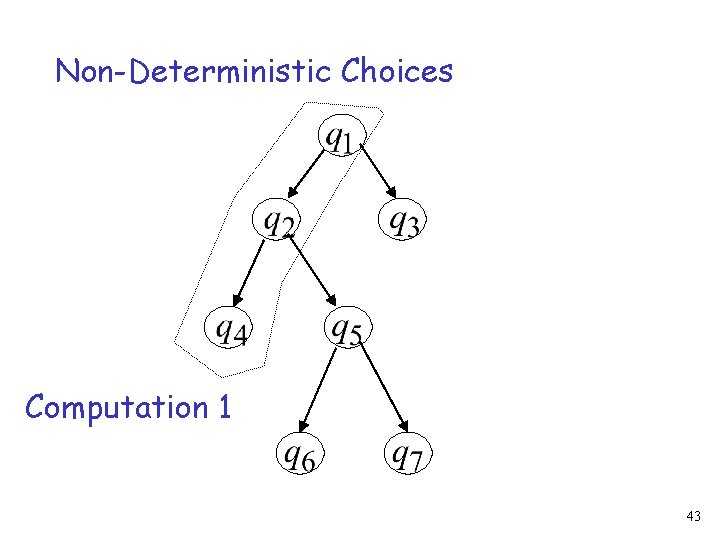
Non-Deterministic Choices Computation 1 43

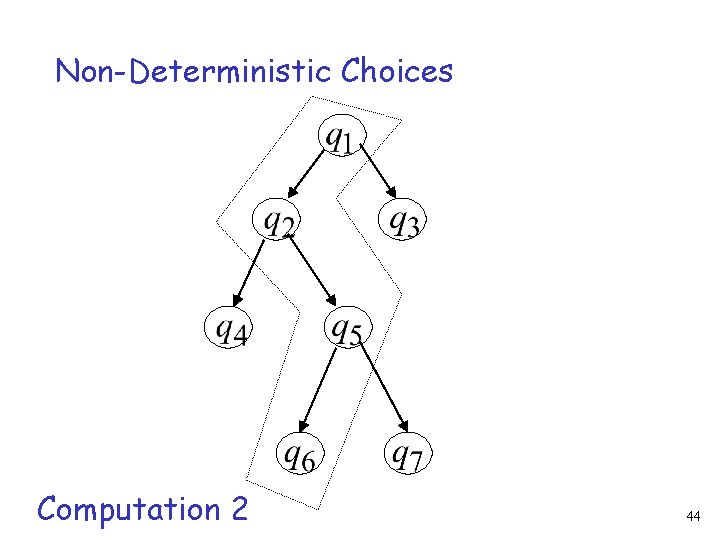
Non-Deterministic Choices Computation 2 44

Simulation Deterministic machine: Keeps track of all possible computations Stores computations in a two-dimensional tape 45

TIME 0 Non. Deterministic Computation 1 46

TIME 1 Non. Deterministic Choice 1 Choice 2 Deterministic Computation 1 Computation 2 47

Repeat Execute a step in each computation: If there is a choice in current computation: replicate configuration change the state in the replica 48

Theorem: Non. Deterministic Machines have the same power with deterministic machines 49

Remark: The simulation in the deterministic Machine takes time exponential time compared to Non. Deterministic machines 50

Polynomial Time in Non. Deterministic Machine NP-Time Polynomial Time in Deterministic Machine P-Time Fundamental Problem: P = NP ? 51