The Sine Rule The Cosine Rule Trigonometrical rules

The Sine Rule The Cosine Rule Trigonometrical rules for finding sides and angles in triangles which are not right angled

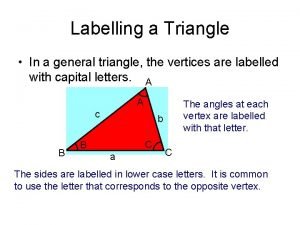
First, a word about labelling triangles…… A c B a b The vertices (corners) of a triangle are usually labelled using capital letters, for example A, B, C C The sides of the triangle are usually labelled using lower case letters, in this case, a, b and c, and are IMPORTANT!! positioned opposite the respective vertices. So Side a will be opposite vertex A Side b will be opposite vertex B Side c will be opposite vertex C Note also that side a could also be called BC as it connects vertex B to vertex C etc…. (We won’t be using this labelling system in this unit of work)

A quick overview of the two rules We will look at the two rules very briefly before starting to use them!

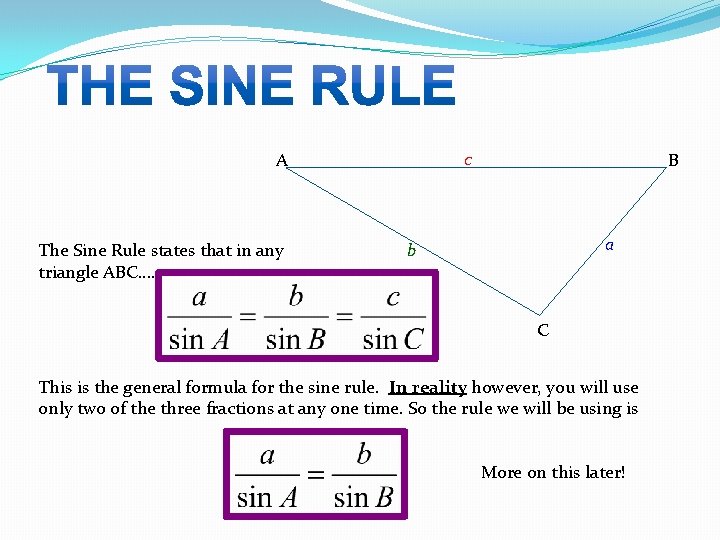
c A The Sine Rule states that in any triangle ABC…. B a b C This is the general formula for the sine rule. In reality however, you will use only two of the three fractions at any one time. So the rule we will be using is More on this later!

c A The Cosine Rule states that in any triangle ABC…. This formula has c 2 as the subject, but the letters can be interchanged, so it can also be written as or B a b C Study the patterns and locations of the letters in the three formulae closely. More on the cosine rule later!

The Sine Rule

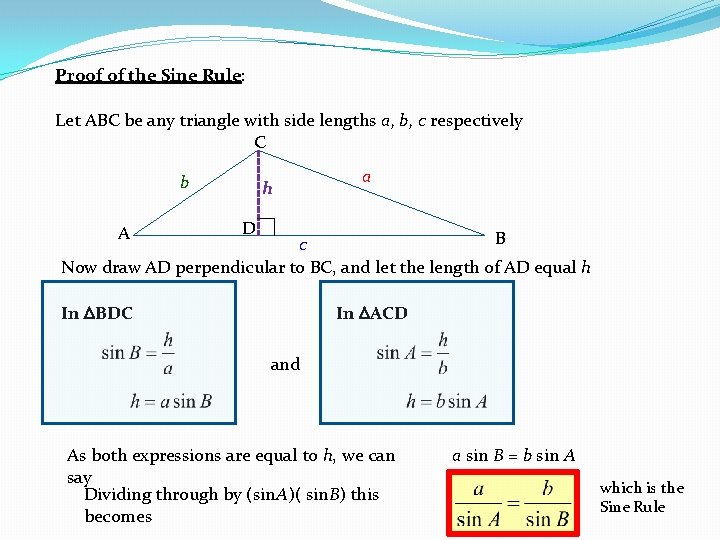
Proof of the Sine Rule: Let ABC be any triangle with side lengths a, b, c respectively C b A h a D B c Now draw AD perpendicular to BC, and let the length of AD equal h In BDC In ACD and As both expressions are equal to h, we can say Dividing through by (sin. A)( sin. B) this becomes a sin B = b sin A which is the Sine Rule

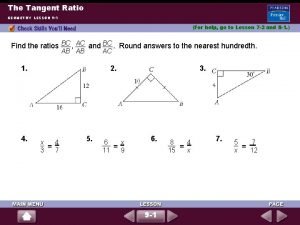
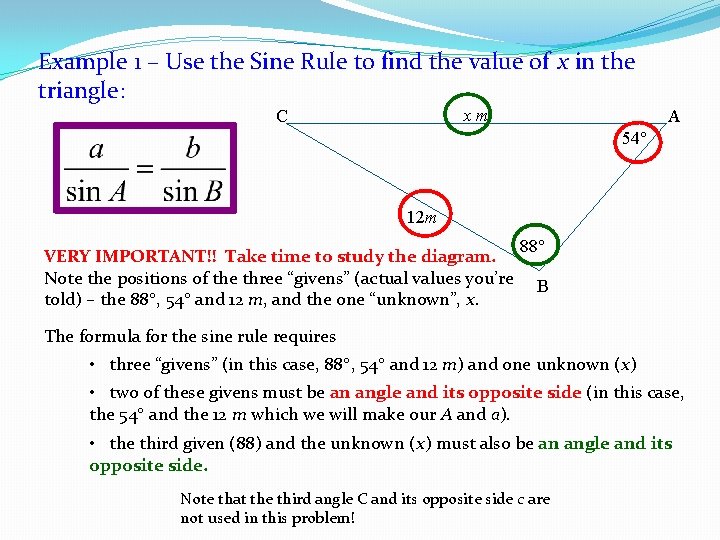
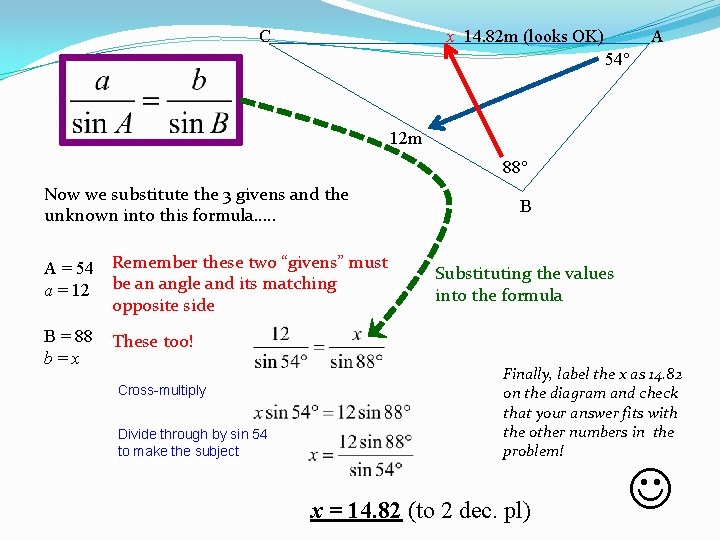
Example 1 – Use the Sine Rule to find the value of x in the triangle: xm C A 54 12 m VERY IMPORTANT!! Take time to study the diagram. Note the positions of the three “givens” (actual values you’re told) – the 88 , 54 and 12 m, and the one “unknown”, x. 88 B The formula for the sine rule requires • three “givens” (in this case, 88 , 54 and 12 m) and one unknown (x) • two of these givens must be an angle and its opposite side (in this case, the 54 and the 12 m which we will make our A and a). • the third given (88) and the unknown (x) must also be an angle and its opposite side. Note that the third angle C and its opposite side c are not used in this problem!

x 14. 82 m (looks OK) C A 54 12 m 88 Now we substitute the 3 givens and the unknown into this formula…. . A = 54 Remember these two “givens” must a = 12 be an angle and its matching opposite side B = 88 b=x B Substituting the values into the formula These too! Cross-multiply Divide through by sin 54 to make the subject Finally, label the x as 14. 82 on the diagram and check that your answer fits with the other numbers in the problem! x = 14. 82 (to 2 dec. pl)

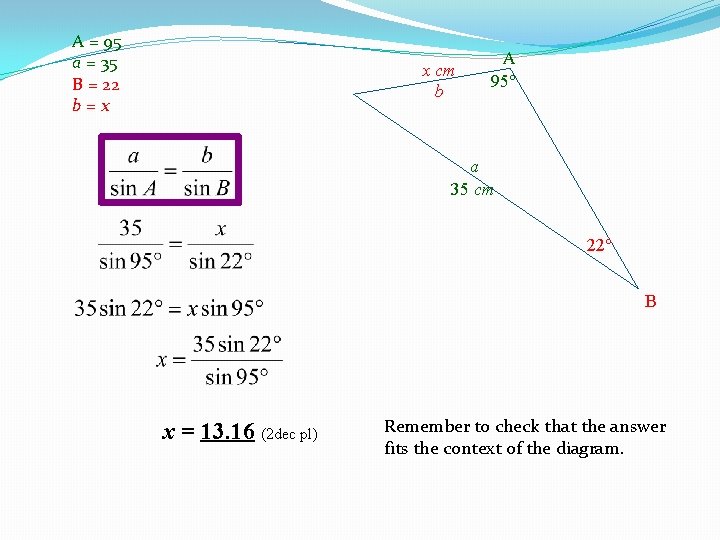
Example 2 – Use the Sine Rule to find the value of x in the triangle: x cm Here, no vertices are labelled so we will have to create our own. But first… 95 35 cm Step 1, check that there are 4 “labels” – i. e. 3 givens and 1 unknown. There a 95 , 22 , 35 cm and x cm so this fits our requirements. Step 2, check that 2 of the 3 givens are a matching angle and opposite side. 95 and 35 cm fit this. Also check that the remaining given and the unknown form another matching angle and opposite side (22 and x cm). They do! All our requirements are in place so we can now use the Sine Rule! A = 95 a = 35 Step 3, Allocate letters A, a, B, b (or any B = 22 other letters of your choice) to matching b=x pairs. 22

A = 95 a = 35 B = 22 b=x x cm b A 95 a 35 cm 22 B x = 13. 16 (2 dec pl) Remember to check that the answer fits the context of the diagram.

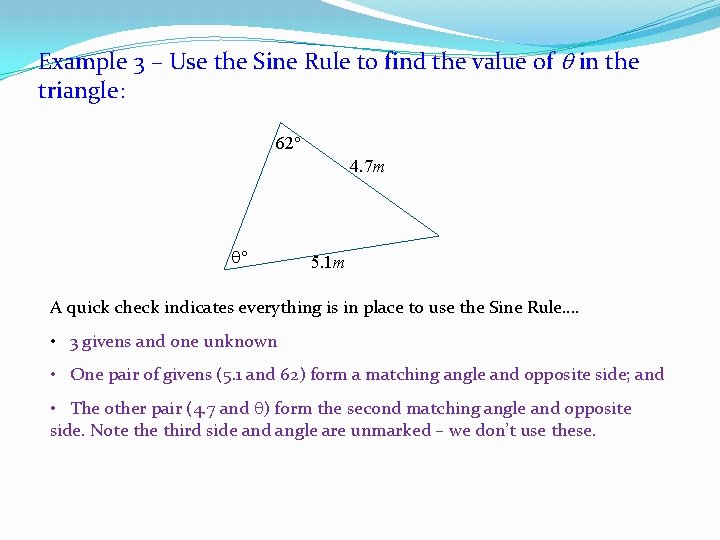
Example 3 – Use the Sine Rule to find the value of in the triangle: 62 4. 7 m 5. 1 m A quick check indicates everything is in place to use the Sine Rule…. • 3 givens and one unknown • One pair of givens (5. 1 and 62) form a matching angle and opposite side; and • The other pair (4. 7 and ) form the second matching angle and opposite side. Note third side and angle are unmarked – we don’t use these.

62 4. 7 m 5. 1 m Remember to check that the answer fits the context of the diagram.

Example 4 – Use the Sine Rule to find the value of x in the triangle: Looking at the diagram, it seems we have a problem! Although the 68 and 35. 7 form a matching angle and opposite side, the 33 and x do not. 35. 7 m 79 But…remembering the angle sum of a triangle is 180 , 68 we can work out the 3 rd angle to be 180 – 33 – 68 = 79. So now we use the 79 as the matching angle for the x and proceed as usual, ignoring the 33 which plays no further part. x = 37. 80 (2 dec pl) 33 xm

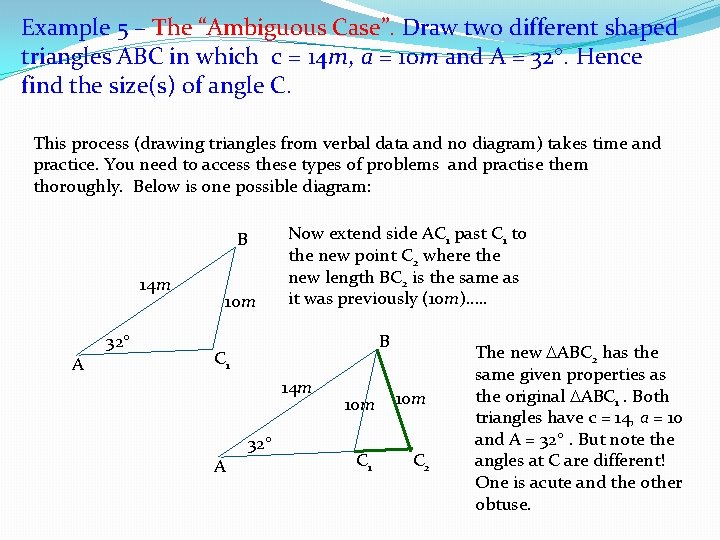
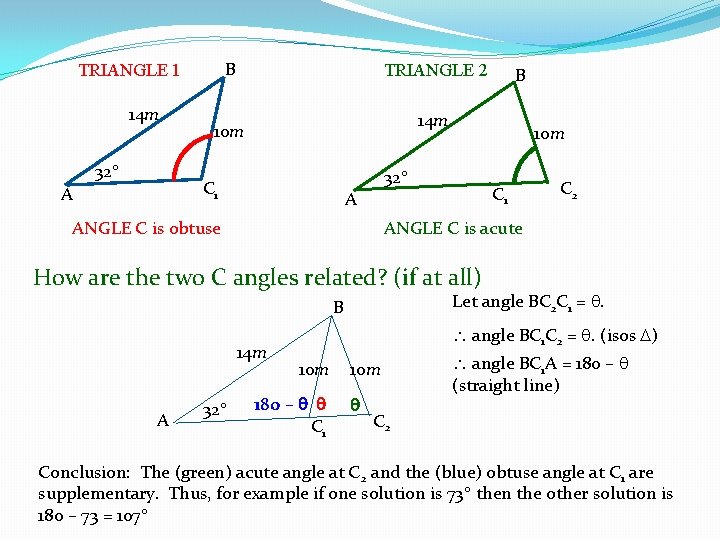
Example 5 – The “Ambiguous Case”. Draw two different shaped triangles ABC in which c = 14 m, a = 10 m and A = 32. Hence find the size(s) of angle C. This process (drawing triangles from verbal data and no diagram) takes time and practice. You need to access these types of problems and practise them thoroughly. Below is one possible diagram: B 14 m 32 A 10 m Now extend side AC 1 past C 1 to the new point C 2 where the new length BC 2 is the same as it was previously (10 m)…. . B C 1 14 m 32 A 10 m C 1 C 2 The new ABC 2 has the same given properties as the original ABC 1. Both triangles have c = 14, a = 10 and A = 32 . But note the angles at C are different! One is acute and the other obtuse.

B TRIANGLE 1 14 m 32 TRIANGLE 2 14 m 10 m C 1 A B 10 m 32 A ANGLE C is obtuse C 1 C 2 ANGLE C is acute How are the two C angles related? (if at all) Let angle BC 2 C 1 = . B 14 m A 32 angle BC 1 C 2 = . (isos ) 10 m 180 – C 1 10 m angle BC 1 A = 180 – (straight line) C 2 Conclusion: The (green) acute angle at C 2 and the (blue) obtuse angle at C 1 are supplementary. Thus, for example if one solution is 73 then the other solution is 180 – 73 = 107

Back to the question! Draw the triangle with the acute, rather than the obtuse, angle at C. B 14 m A 32 10 m C 2 Applying the Sine Rule, One solution (the acute angle which is the only one given by the calculator) is therefore 47. 9 and the second solution (the obtuse angle) is 180 – 47. 9 = 132. 1 Ans: = 47. 9 or 132. 1

• The Sine Rule can be used to find unknown sides or angles in triangles. • The Sine Rule formula is • To use the Sine Rule, you must have q A matching angle and opposite side pair (two givens) q A third given and an unknown, which also make an angle and opposite side pair • When asked to find the size of an ANGLE, first check whether the problem could involve the ambiguous case (see Example 5). In that case, the two answers are supplementary – i. e. add to 180 • When confronted with a problem where you have to decide whether to use the Sine Rule or the Cosine Rule, always try for the Sine Rule first, as it is easier. We will have this discussion later! • In every triangle, the largest side is always opposite the largest angle. The side lengths are in the ratio of the sines of their opposite angles.

In every triangle, q The largest side is always opposite the largest angle. q The middle sized side is always opposite the middle sized angle, and q The smallest side is always opposite the smallest angle • The ratio of any two side lengths is always equal to the ratio of the sines of their respective opposite angles. A b C c a B These are just re-shaped versions of the original sine rule formulae.

The Cosine Rule There are two variations of this…. To find a side use To find an angle use c 2 = a 2 + b 2 – 2 ab cos C These formulae are just rearrangements of each other. Verify this as an exercise.

Proof of the Cosine Rule: Let ABC be any triangle with side lengths a, b, c respectively A b C c h x D a NOTE!! The expansion (a – x)2 = a 2 – 2 ax + x 2 a–x B Now draw AD perpendicular to BC, and let the length of AD equal h Let the length CD = x, and so length BD will be a – x. In ACD In ABD Pythagoras gives In ACD Pythagoras gives (3) (1) (2) The formulae (2) and (3) are both for h 2 so we make them equal to each other.

Now cancel the x 2 on each side and make c 2 the subject… (4) From the first box on the previous slide, taking result (1) x = b cos C and substituting this into (4), we get which is a version of the Cosine Rule (for finding a side)

Cosine Rule – Finding a SIDE c 2 = a 2 + b 2 – 2 ab cos C (1) Note the positions of the letters. If the 2 ab cos C were missing, this would just be Pythagoras’ Theorem, c 2 = a 2 + b 2. If the triangle were right angled, then C would be 90 and as cos 90 = 0, it becomes Pythagoras’ Theorem! (2) When c 2 is the subject, the only angle in the formula is C (the angle opposite to side c). Note A and B are absent from the formula. (3) The above formula is to find a side length. The letters can be swapped around and the same formula can be written a 2 = b 2 + c 2 – 2 bc cos A b 2 = a 2 + c 2 – 2 ac cos B c 2 = a 2 + b 2 – 2 ab cos C Here are three variations of the formula shown together. Study them closely and note the patterns!

Cosine Rule – Finding an ANGLE c 2 = a 2 + b 2 – 2 ab cos C (4) This formula can be rearranged to make cos C the subject, i. e. This is the version of the Cosine Rule to use when FINDING AN ANGLE. (5) Again, the letters can be swapped around and the same formula can be written

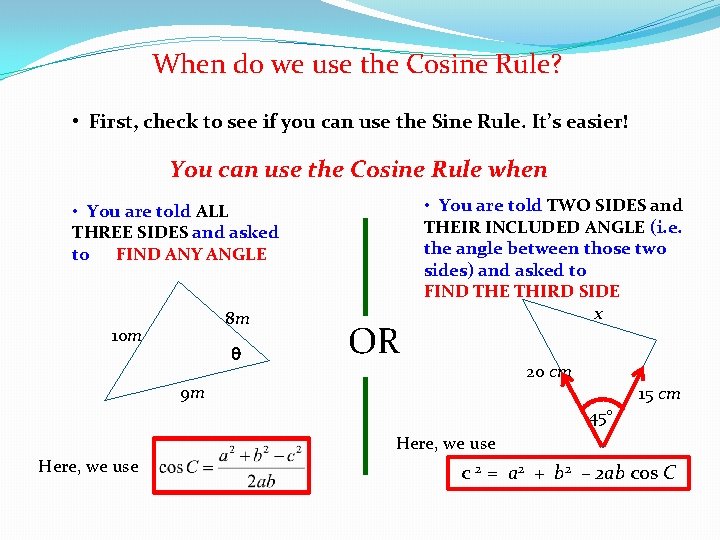
When do we use the Cosine Rule? • First, check to see if you can use the Sine Rule. It’s easier! You can use the Cosine Rule when • You are told ALL THREE SIDES and asked to FIND ANY ANGLE 8 m 10 m OR • You are told TWO SIDES and THEIR INCLUDED ANGLE (i. e. the angle between those two sides) and asked to FIND THE THIRD SIDE x 20 cm 9 m 15 cm 45 Here, we use c 2 = a 2 + b 2 – 2 ab cos C

Example 6 – Use the Cosine Rule to find the value of c in the triangle: C 65 Finally, check that c = 3. 85 fits the diagram. 4 cm 3 cm A B c Note that we have 2 given sides (3 cm and 4 cm) and their included angle (65 ) so we can use the Cosine Rule for finding a side… c 2 = a 2 + b 2 – 2 ab cos C Let a=3 b=4 C = 65 c 2 = 32 + 42 – 2 × 3× 4 × cos 65 c 2 = 14. 857 (do in one step on calculator) c = 3. 85 (to two dec pl) Ans: The length of the required side is 3. 85 cm

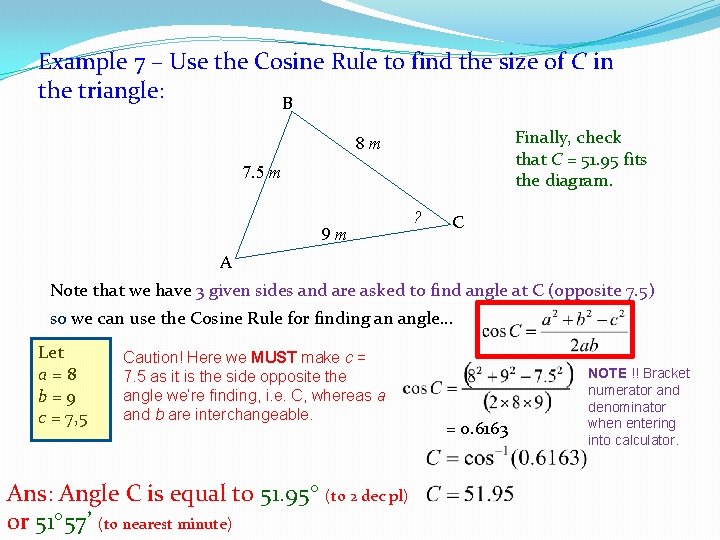
Example 7 – Use the Cosine Rule to find the size of C in the triangle: B Finally, check that C = 51. 95 fits the diagram. 8 m 7. 5 m 9 m ? C A Note that we have 3 given sides and are asked to find angle at C (opposite 7. 5) so we can use the Cosine Rule for finding an angle… Let a=8 b=9 c = 7, 5 Caution! Here we MUST make c = 7. 5 as it is the side opposite the angle we’re finding, i. e. C, whereas a and b are interchangeable. Ans: Angle C is equal to 51. 95 (to 2 dec pl) or 51 57’ (to nearest minute) = 0. 6163 NOTE !! Bracket numerator and denominator when entering into calculator.

Example 8 – Use the Cosine Rule to find the value of x in the triangle: 10 m 100 11 m x Finally, check that x = 16. 10 fits the diagram. x is the longest side so this would seem reasonable. Note that we have 2 given sides (10 m and 11 cm) and their included angle (100 ) so we use the Cosine Rule for finding a side… Let a = 10 b = 11 c=x C = 100 c 2 = a 2 + b 2 – 2 ab cos C x 2 = 102 + 112 – 2 × 10 × 11 × cos 100 x 2 = 259. 2 (do in one step on calculator) x = 16. 10 (to two dec pl) Ans: The length of the required side is 16. 10 m

Example 9 – Use the Cosine Rule to find the value of in the triangle: 40 mm 29 mm 21 mm Finally, check that = 105 fits the diagram. LOOKS obtuse so this would seem reasonable. Beware – you can’t always presume the drawings are to scale, so be careful when judging the appropriateness of your answers (in all problems) Note that we have 3 given sides and are asked to find angle opposite to 40 mm so we use the Cosine Rule for finding an angle… Let a = 21 b = 29 c = 40 C= remember the brackets Note the negative cos. This means our angle is obtuse! ALL OBTUSE ANGLES HAVE A NEGATIVE COSINE! = 105. 13 Ans: is approx. equal to 105. 13 (to 2 dec pl) or 105 8’ (to nearest min)

• The Cosine Rule can be used to find unknown sides or angles in triangles. • There are two versions of the Cosine Rule formula and three variations within each of these, depending on what is required as the subject To find a SIDE To find an ANGLE c 2 = a 2 + b 2 – 2 ab cos C a 2 = b 2 + c 2 – 2 bc cos A b 2 = a 2 + c 2 – 2 ac cos B Make sure you familiarise yourself with how the PATTERNS in these configurations work. Also remember each formula on the left is just a rearrangement of its corresponding formula on the right.

• To use the Cosine Rule to find an angle you must be given all three sides • To use the Cosine Rule to find a side you must be given the other two sides and their included angle. • When deciding whether to use the Sine Rule or the Cosine Rule, always try the Sine Rule first, as it is easier (only one formula to deal with). • When dealing with angles in the range 90 < < 180 , i. e. OBTUSE ANGLES, remember that their cosines are negative. This does not apply to their sines – they are still positive.

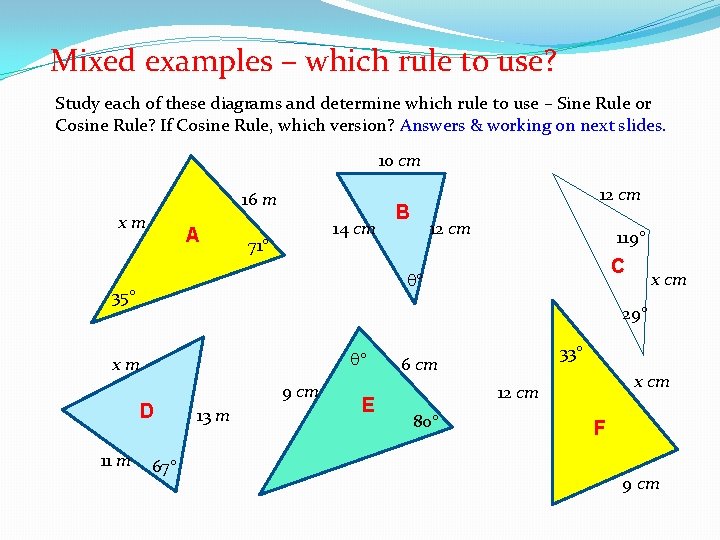
Mixed examples – which rule to use? Study each of these diagrams and determine which rule to use – Sine Rule or Cosine Rule? If Cosine Rule, which version? Answers & working on next slides. 10 cm 16 m xm A 14 cm 71 B 12 cm 119 C 35 x cm 29 xm D 11 m 12 cm 67 9 cm 13 m E 33 6 cm x cm 12 cm 80 F 9 cm

Example 10 First check to see if we can use the Sine Rule. 16 m xm 35 A 71 We have a given angle and opposite side (35 and 16 m), and the unknown x and the other given (71 ) also form a matching angle and opposite pair. So we can use the SINE RULE Ans: the length of side x is 26. 38 m approximately. to two dec pl. Remember to check appropriateness of your answer!

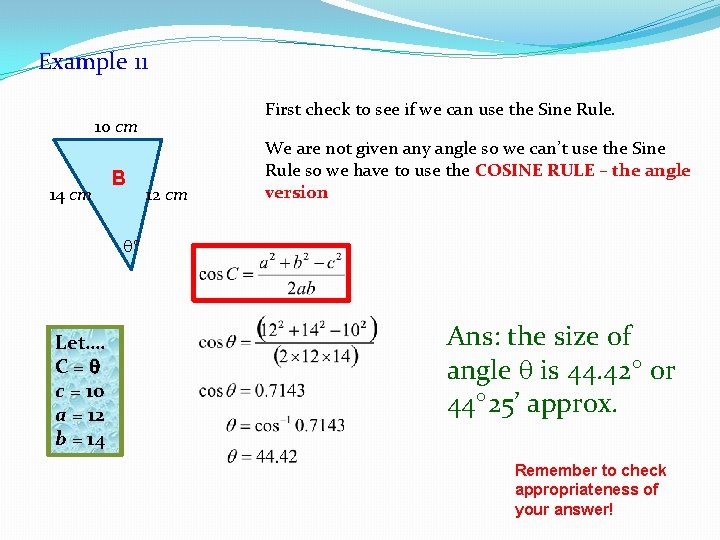
Example 11 First check to see if we can use the Sine Rule. 10 cm 14 cm B 12 cm We are not given any angle so we can’t use the Sine Rule so we have to use the COSINE RULE – the angle version Let…. C= c = 10 a = 12 b = 14 Ans: the size of angle is 44. 42 or 44 25’ approx. Remember to check appropriateness of your answer!

Example 12 12 cm 32 119 C 29 Let…. a=x A = 32 b = 12 B = 29 First check to see if we can use the Sine Rule. x cm We have a given angle and opposite side (29 and 12 cm), but the unknown x and the other given (119 ) are NOT a matching angle and opposite pair. BUT…the third angle is 180 – 119 – 29 = 32 so we can use the SINE RULE Ans: the length of side x is 13. 12 cm approximately. to two dec pl. Remember to check appropriateness of your answer!

Example 13 First check to see if we can use the Sine Rule. xm D 11 m 13 m We are not given any angle and matching opposite side so we can’t use the Sine Rule, so we have to use the COSINE RULE – the side version 67 c 2 = a 2 + b 2 – 2 ab cos C Let…. C = 67 c=x a = 11 b = 13 x 2 = 112 + 132 – 2 × 11 × 13 × cos 67 x 2 = 178. 251 Ans: the size of side x is x = 13. 35 m (to 2 dec places) Remember to check appropriateness of your answer!

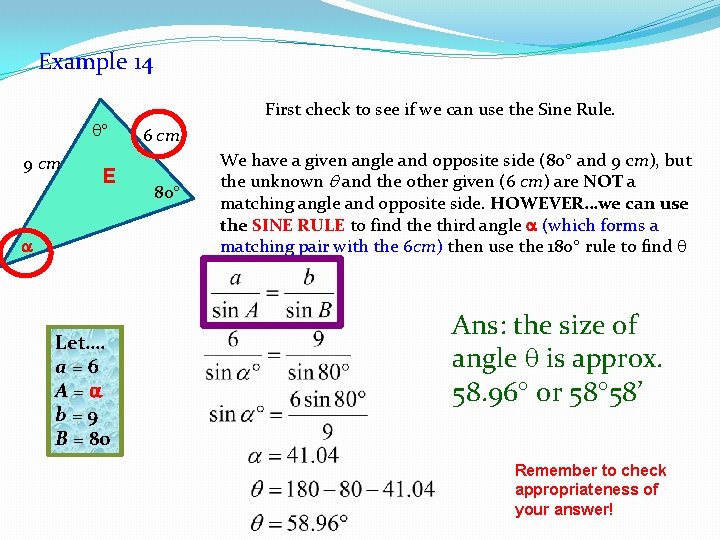
Example 14 9 cm E Let…. a=6 A= b=9 B = 80 First check to see if we can use the Sine Rule. 6 cm 80 We have a given angle and opposite side (80 and 9 cm), but the unknown and the other given (6 cm) are NOT a matching angle and opposite side. HOWEVER…we can use the SINE RULE to find the third angle (which forms a matching pair with the 6 cm) then use the 180 rule to find Ans: the size of angle is approx. 58. 96 or 58 58’ Remember to check appropriateness of your answer!

Example 15 First check to see if we can use the Sine Rule. We have a given angle and opposite side (33 and 9 cm), but the unknown x and the other given (12 cm) are insufficient data 33 for Sine Rule. The Cosine Rule won’t work either as the x cm triangle’s data does not match either of the two configurations 12 cm for the Cosine Rule. HOWEVER…if we let be the angle F opposite the 12 cm we then have a second matching pair and can begin with using the SINE RULE to find angle . (This is PART 1) 9 cm NOW FOR PART 2 …. . Once we know we can then find the third angle (which is opposite to x) and then apply the Sine Rule a second time to find x. Part 1 (finding ) Part 2 (finding x) Finding = 180 – 33 – 46. 57 = 100. 43 Note!! Here the diagram is quite out of scale. This becomes apparent on checking the reasonableness of your answer