Language Recognition 11 4 and Turing Machines 11









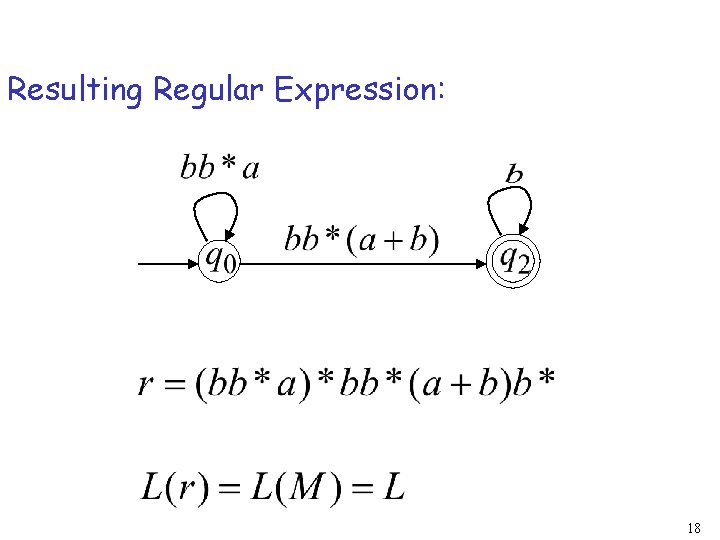






















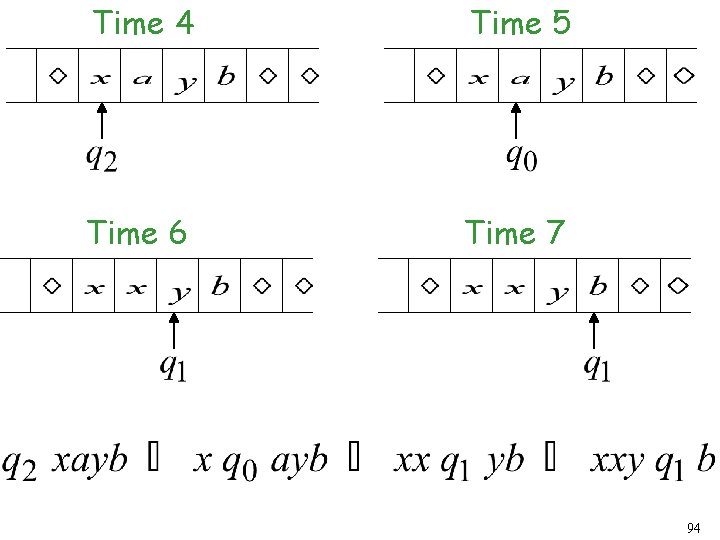














- Slides: 134

Language Recognition (11. 4) and Turing Machines (11. 5) Longin Jan Latecki Temple University Based on slides by Costas Busch from the course http: //www. cs. rpi. edu/courses/spring 05/modcomp/ and … 1

Three Equivalent Representations Regular expressions Finite automata Each can describe the others Regular languages Kleene’s Theorem: For every regular expression, there is a deterministic finite-state automaton that defines the same language, and vice versa. 2

NFAs Regular grammars Thus, the language recognized by FSA is a regular language Every NFA can be converted into a corresponding regular grammar and vice versa. Each symbol A of the grammar is associated with a nonterminal node of the NFA s. A, in particular, start symbol S is associated with the start state s. S. Every transition is associated with a grammar production: T(s. A, a) = s. B A a. B. Every production B is associated with final state s. B. See Ex. 3, p. 771, and Ex. 4, p. 772. 3

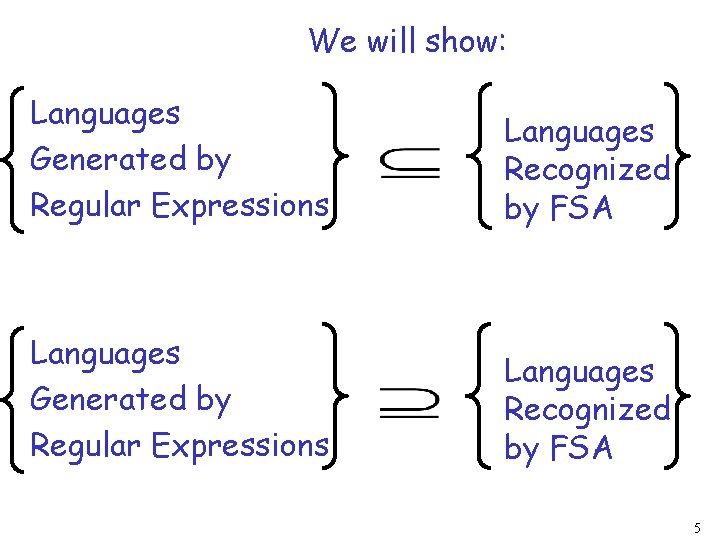
Kleene’s Theorem Languages Generated by Regular Expressions Languages Recognized by FSA 4

We will show: Languages Generated by Regular Expressions Languages Recognized by FSA 5

Proof - Part 1 Languages Generated by Regular Expressions Languages Recognized by FSA For any regular expression the language is recognized by FSA (= is a regular language) Proof by induction on the size of 6

Induction Basis Primitive Regular Expressions: NFAs regular languages 7

Inductive Hypothesis Assume for regular expressions and that and are regular languages 8

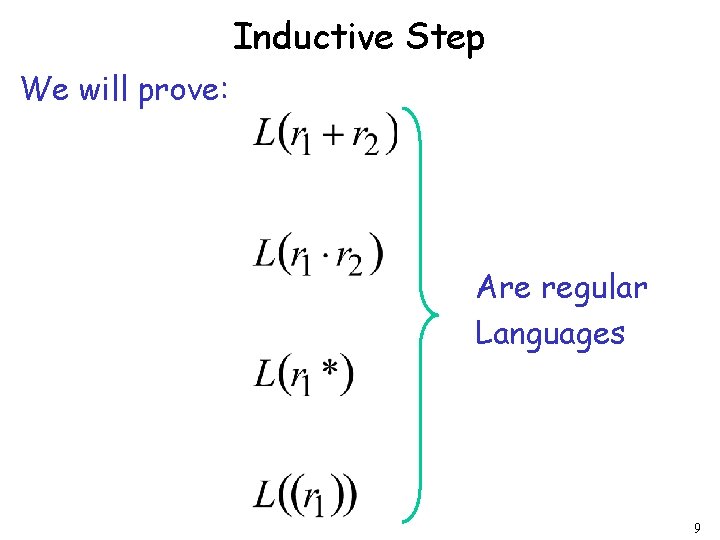
Inductive Step We will prove: Are regular Languages 9

By definition of regular expressions: 10

By inductive hypothesis we know: and are regular languages We need to show: Regular languages are closed under: Union Concatenation Star 11

Therefore: Are regular languages And trivially: is a regular language 12

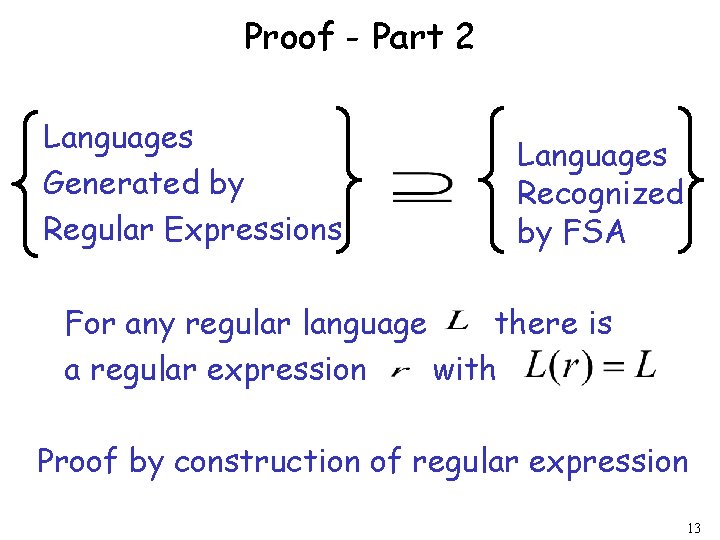
Proof - Part 2 Languages Generated by Regular Expressions Languages Recognized by FSA For any regular language there is a regular expression with Proof by construction of regular expression 13

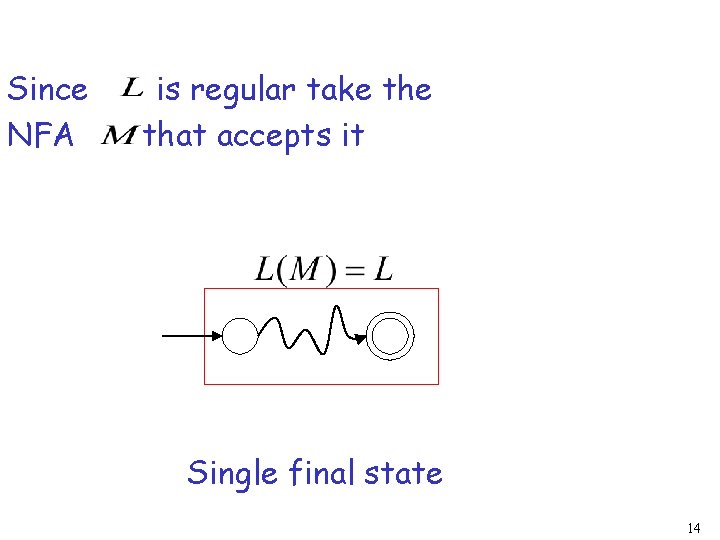
Since NFA is regular take that accepts it Single final state 14

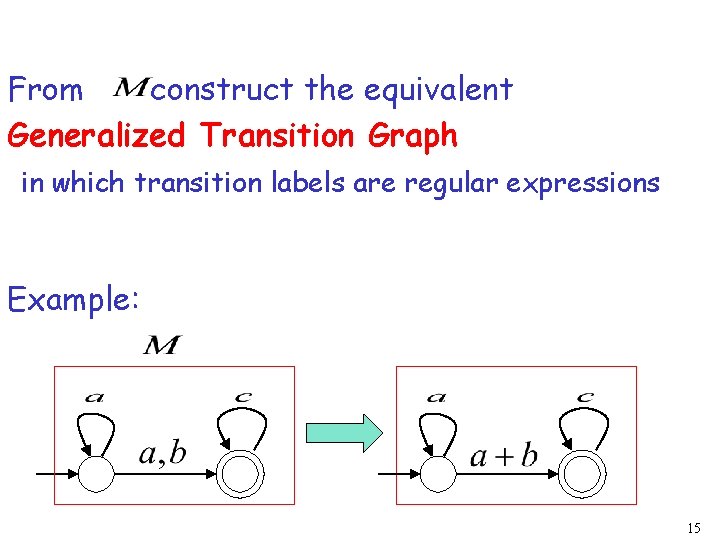
From construct the equivalent Generalized Transition Graph in which transition labels are regular expressions Example: 15

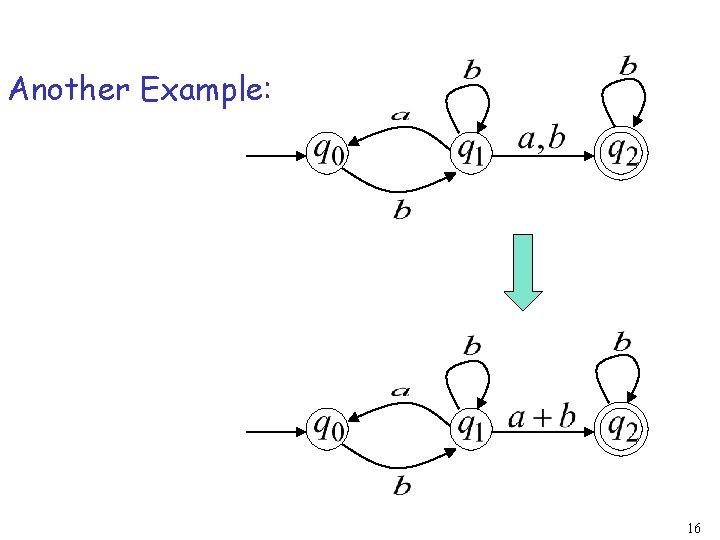
Another Example: 16

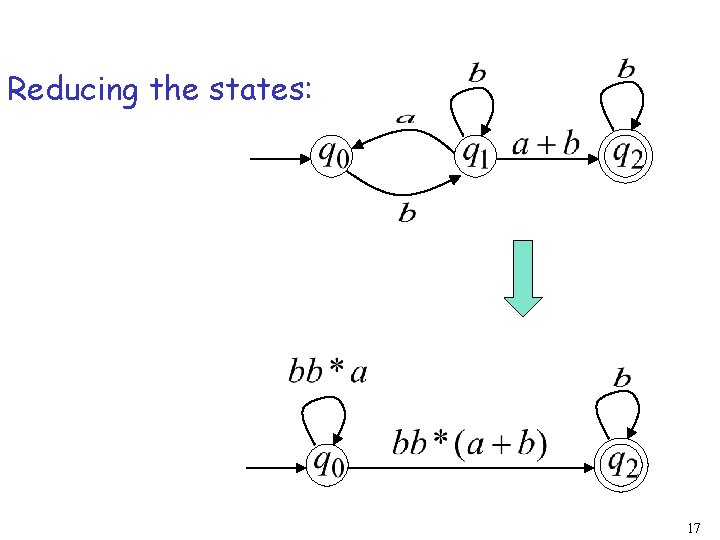
Reducing the states: 17
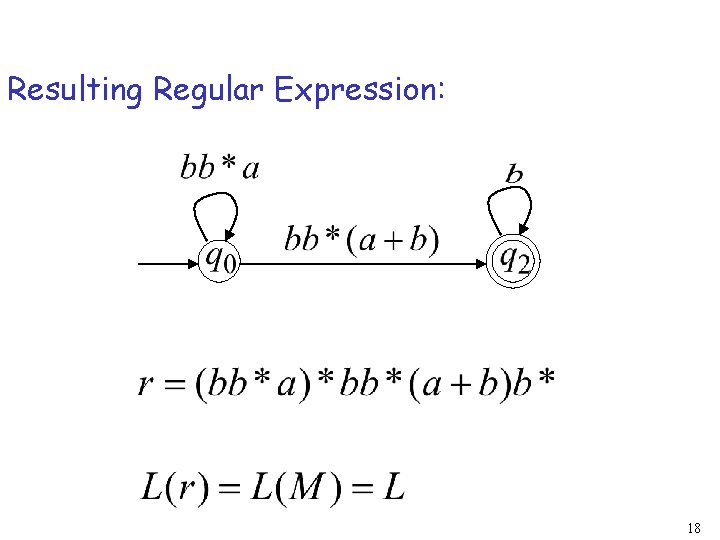
Resulting Regular Expression: 18

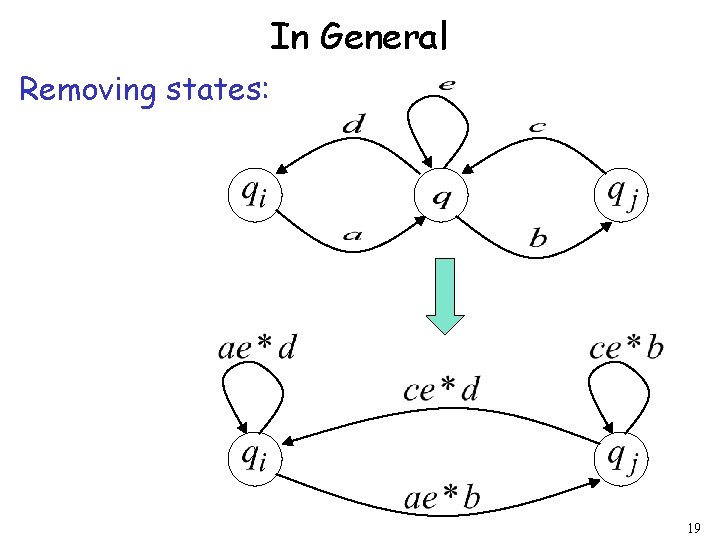
In General Removing states: 19

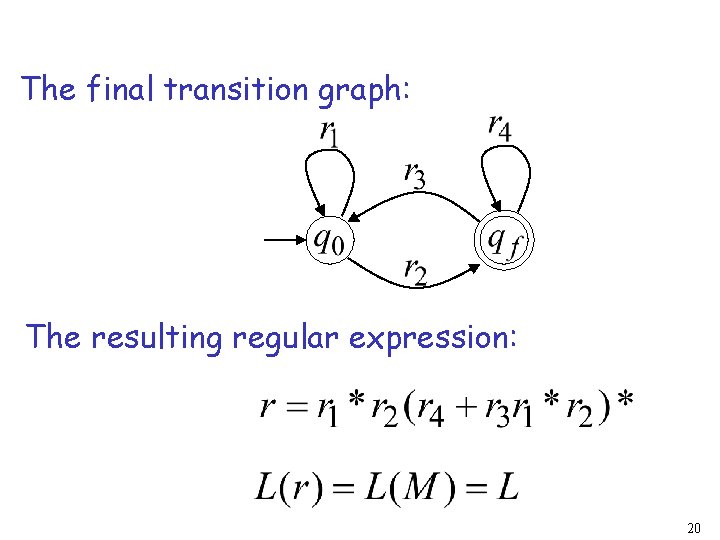
The final transition graph: The resulting regular expression: 20

Models of computing DFA Push down automata Bounded Turing M’s Turing machines - regular languages Context-free Context sensitive Phrase-structure 21

Foundations The theory of computation and the practical application it made possible — the computer — was developed by an Englishman called Alan Turing. 22

Alan Turing 1912 (23 June): Birth, Paddington, London 1939 -42: Breaking of U-boat Enigma, saving battle of the Atlantic 1931 -34: Undergraduate at King's College, Cambridge University 1946: Computer and software design leading the world. 1932 -35: Quantum mechanics, probability, logic 1948: Manchester University 1936: The Turing machine, computability, universal machine 1936 -38: Princeton University. Ph. D. Logic, algebra, number theory 1938 -39: Return to Cambridge. Introduced to German Enigma cipher machine 1939 -40: The Bombe, machine for Enigma decryption 1949: First serious mathematical use of a computer 1950: The Turing Test for machine intelligence 1952: Arrested as a homosexual, loss of security clearance 1954 (7 June): Death (suicide) by cyanide poisoning, Wilmslow, Cheshire. —from Andrew Hodges http: //www. turing. org. uk/turing/ 23

The Decision Problem In 1928 the German mathematician, David Hilbert (1862 -1943), asked whethere could be a mechanical way (i. e. by means of a fully specifiable set of instructions) of determining whether some statement in a formal system like arithmetic was provable or not. In 1936 Turing published a paper the aim of which was to show that there was no such method. “On computable numbers, with an application to the Entscheidungs problem. ” Proceedings of the London Mathematical Society, 2(42): 230 -265). 24

The Turing Machine In order to argue for this claim, he needed a clear concept of “mechanical procedure. ” His idea — which came to be called the Turing machine — was this: (1) A tape of infinite length (2) Finitely many squares of the tape have a single symbol from a finite language. (3) Someone (or something) that can read the squares and write in them. (4) At any time, the machine is in one of a finite number of internal states. (5) The machine has instructions that determine what it does given its internal state and the symbol it encounters on the tape. It can change its internal state; change the symbol on the square; move forward; move backward; halt (i. e. stop). 25

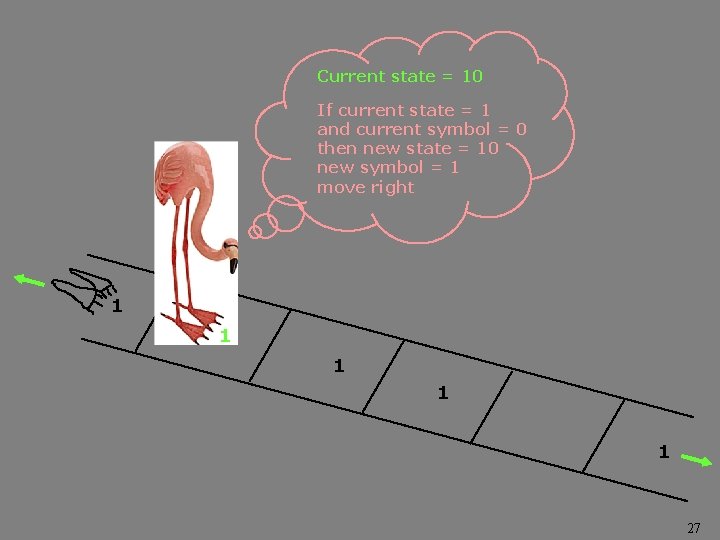
Current state = 10 If current state = 1 and current symbol = 0 then new state = 10 new symbol = 1 move right 1 0 1 1 1 26

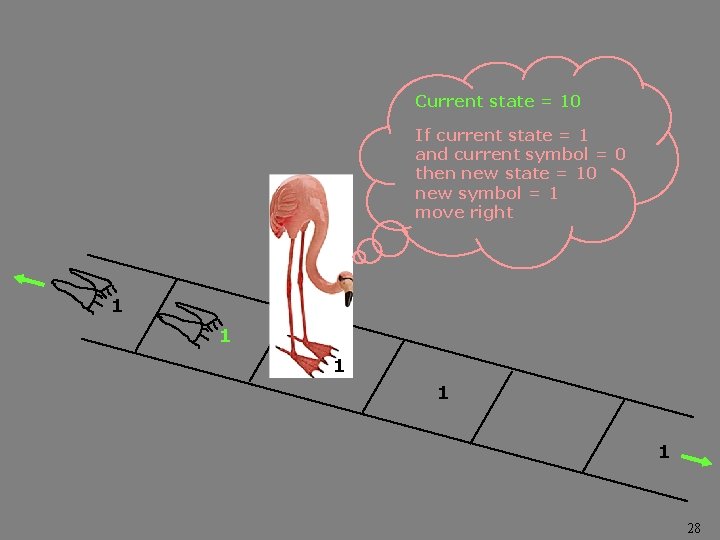
Current state = 10 If current state = 1 and current symbol = 0 then new state = 10 new symbol = 1 move right 1 1 1 27

Current state = 10 If current state = 1 and current symbol = 0 then new state = 10 new symbol = 1 move right 1 1 1 28

Functions It is essential to the idea of a Turing machine that it is not a physical machine, but an abstract one — a set of procedures. It makes no difference whether the machine is embodied by a person in a boxcar on a track, or a person with a paper and pencil, or a smart and well-trained flamingo. 29

Turing’s Theorem In the 1936 paper Turing proved that there are “generalpurpose” Turing machines that can compute whatever any other Turing machine. This is done by coding the function of the special-purpose machine as instructions of the other machine — that is by “programming” it. This is called Turing’s theorem. These are universal Turing machines, and the idea of a coding for a particular function fed into a universal Turing machine is basically our conception of a computer and a stored program. The concept of the universal Turing machine is just the concept of the computer as we know it. 30

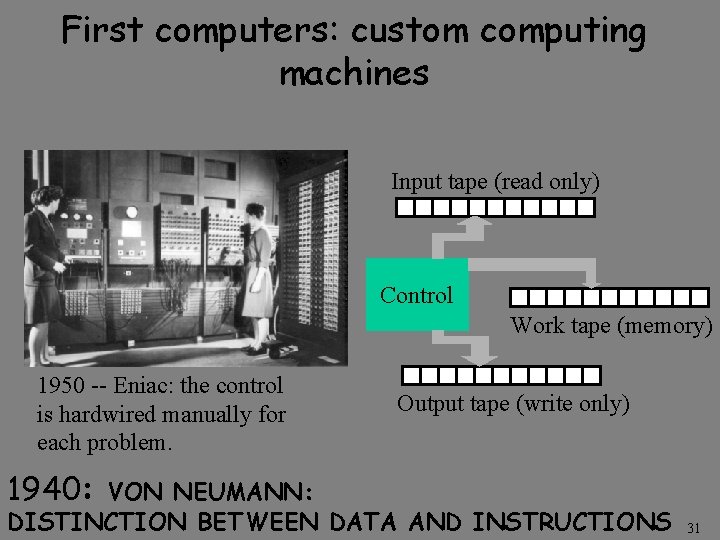
First computers: custom computing machines Input tape (read only) Control Work tape (memory) 1950 -- Eniac: the control is hardwired manually for each problem. Output tape (write only) 1940: VON NEUMANN: DISTINCTION BETWEEN DATA AND INSTRUCTIONS 31

Can Machines Think? In “Computing machinery and intelligence, ” written in 1950, Turing asks whether machines can think. He claims that this question is too vague, and proposes, instead, to replace it with a different one. That question is: Can machines pass the “imitation game” (now called the Turing test)? If they can, they are intelligent. Turing is thus the first to have offered a rigorous test for the determination of intelligence quite generally. 32

The Turing Test The game runs as follows. You sit at a computer terminal and have an electronic conversation. You don’t know who is on the other end; it could be a person or a computer responding as it has been programmed to do. If you can’t distinguish between a human being and a computer from your interactions, then the computer is intelligent. Note that this is meant to be a sufficient condition of intelligence only. There may be other ways to be intelligent. 33

Artificial Intelligence 34

The Church-Turning Thesis Turing, and a logician called Alonzo Church (1903 -1995), independently developed the idea (not yet proven by widely accepted) that whatever can be computed by a mechanical procedure can be computed by a Turing machine. This is known as the Church-Turing thesis. 35

AI: The Argument We’ve now got the materials to show that AI is possible: P 1: Any function that can be computed by a mechanical procedure can be computed by a Turing machine. (Church-Turing thesis) P 2: Thinking is nothing more than the computing of functions by mechanical procedures (i. e. , thinking is symbol manipulation). (Functionalist-Computationalist thesis) C 1: Therefore, thinking can be performed by a Turing machine. P 3: Turing machines are multiply realizable. In particular, they can be realized by computers, robots, etc. It is possible to build a computer, robot, etc. that can think. That is, AI is possible. 36

Turing Machines 37

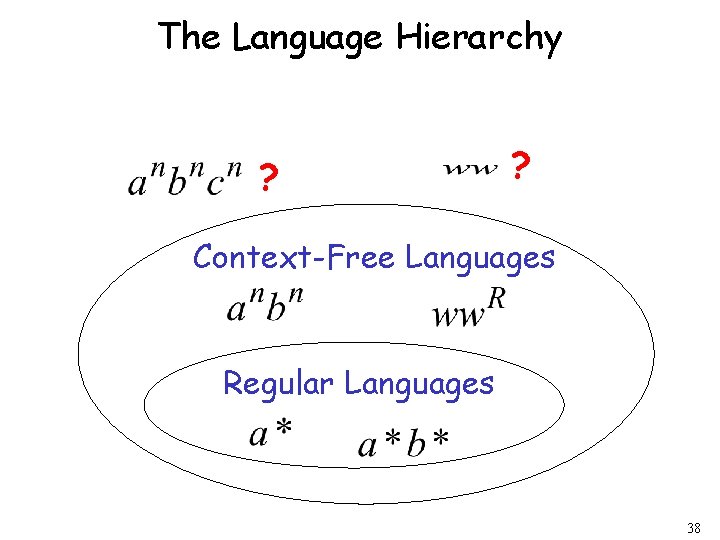
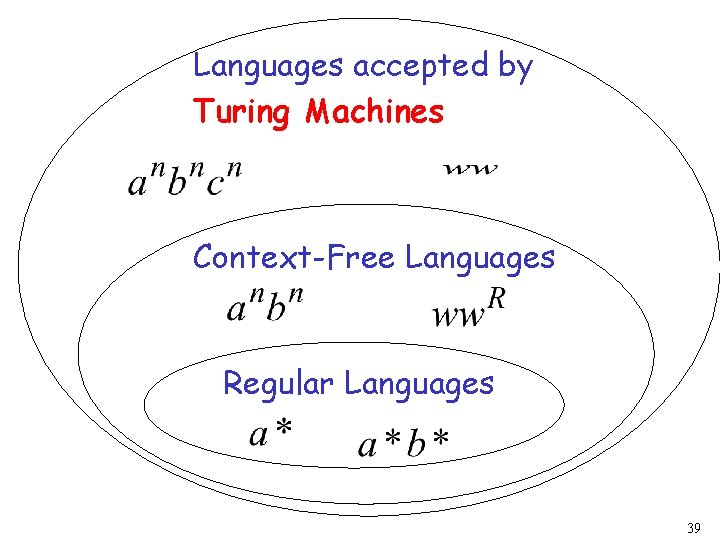
The Language Hierarchy ? ? Context-Free Languages Regular Languages 38

Languages accepted by Turing Machines Context-Free Languages Regular Languages 39

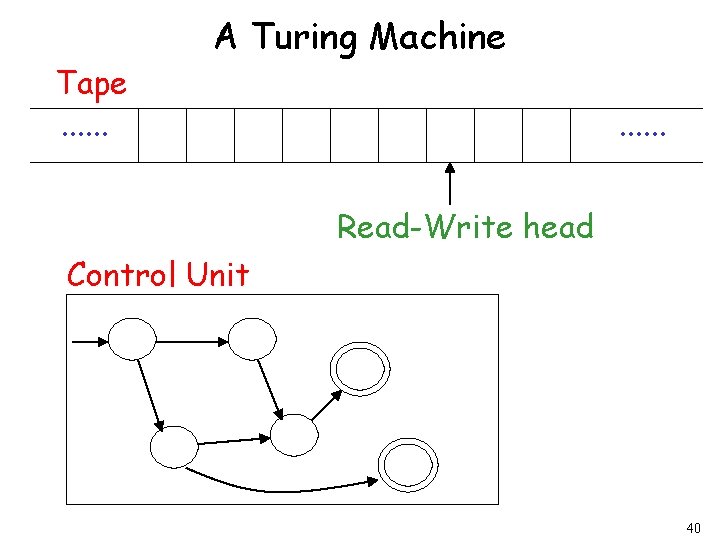
Tape. . . A Turing Machine. . . Read-Write head Control Unit 40

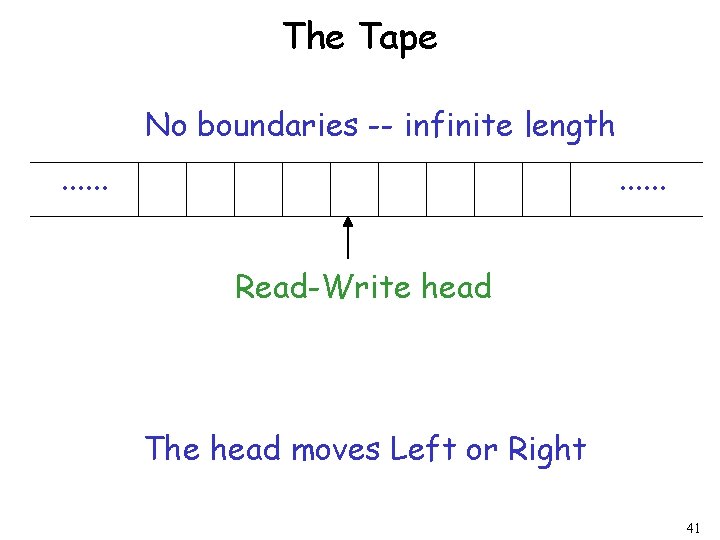
The Tape No boundaries -- infinite length. . . Read-Write head The head moves Left or Right 41

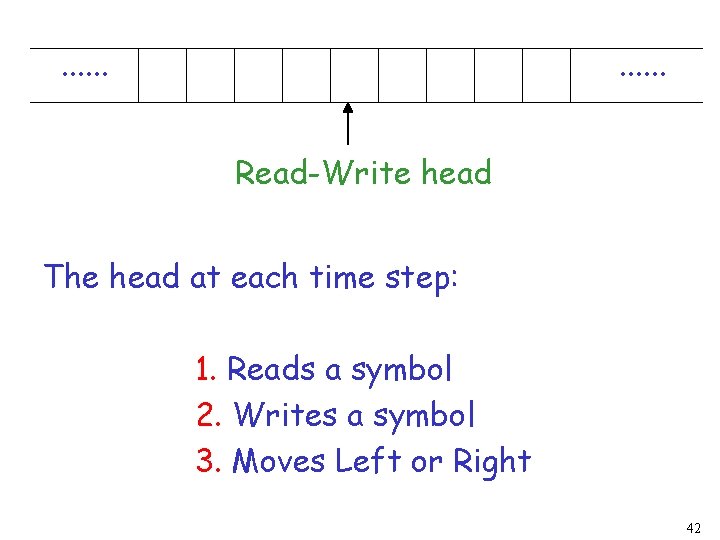
. . . Read-Write head The head at each time step: 1. Reads a symbol 2. Writes a symbol 3. Moves Left or Right 42

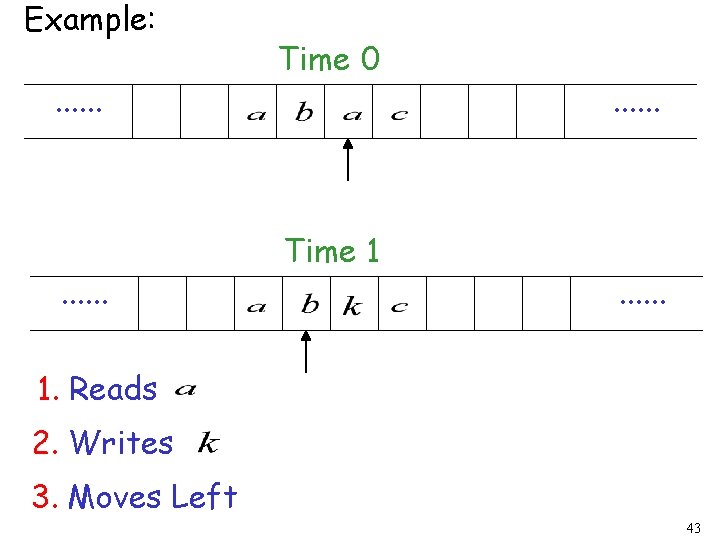
Example: . . . Time 0 Time 1 . . . 1. Reads 2. Writes 3. Moves Left 43

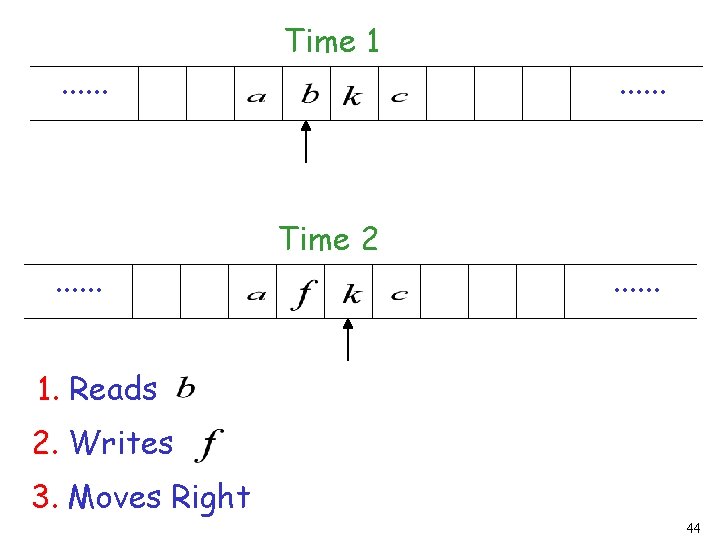
. . . Time 1 Time 2 . . . 1. Reads 2. Writes 3. Moves Right 44

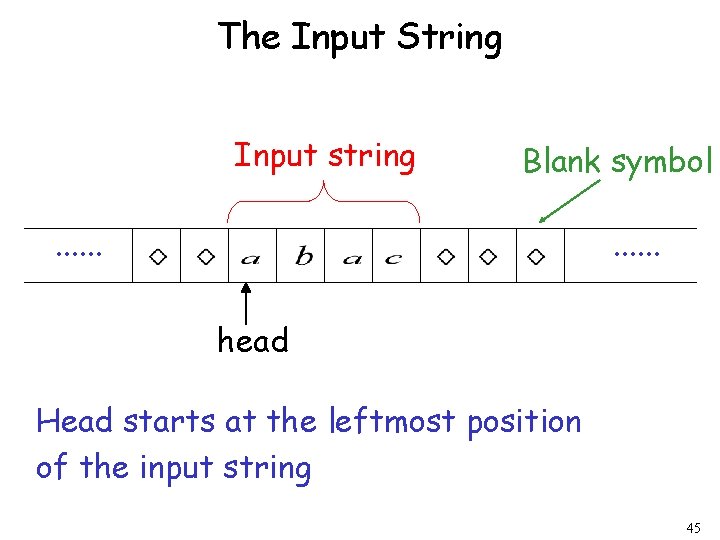
The Input String Input string Blank symbol . . . head Head starts at the leftmost position of the input string 45

Input string. . . Blank symbol. . . head Remark: the input string is never empty 46

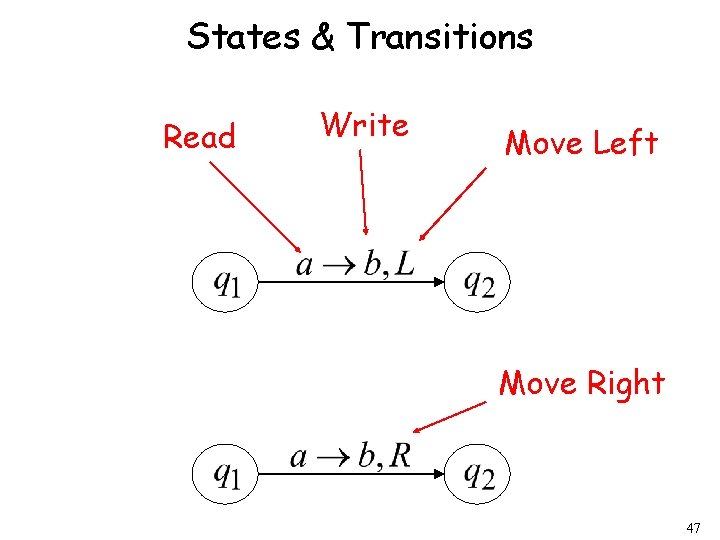
States & Transitions Read Write Move Left Move Right 47

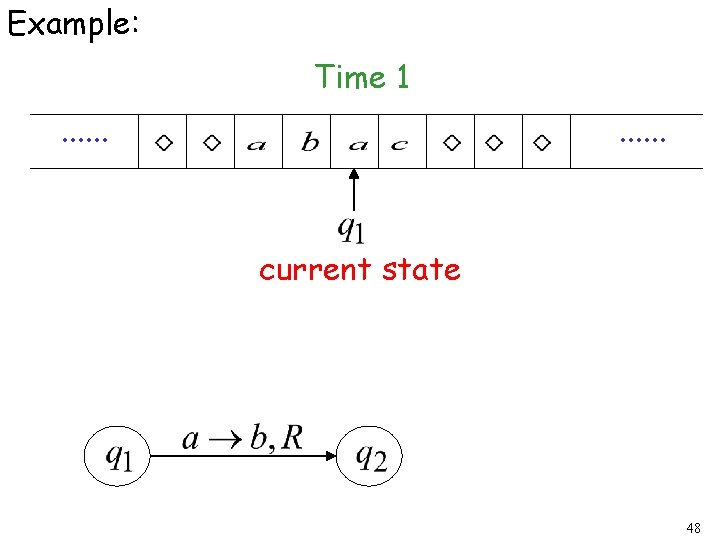
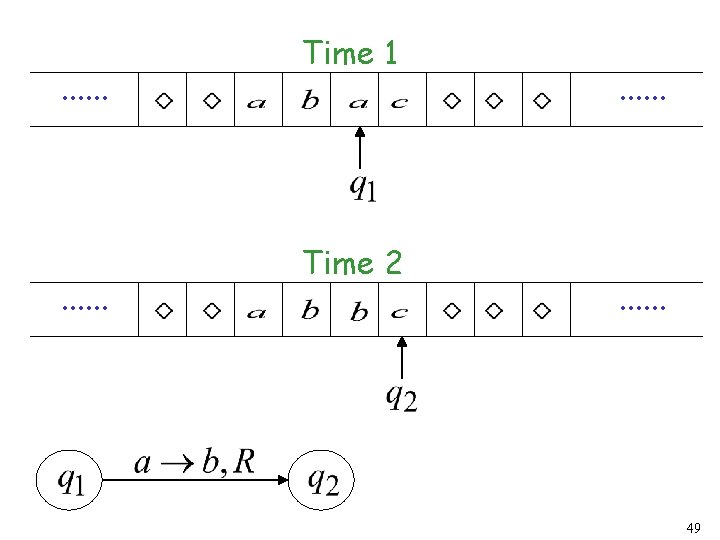
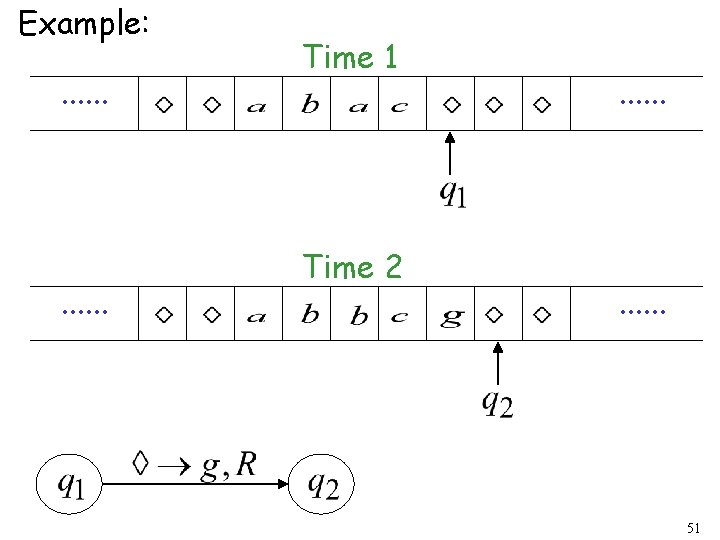
Example: Time 1. . . current state 48

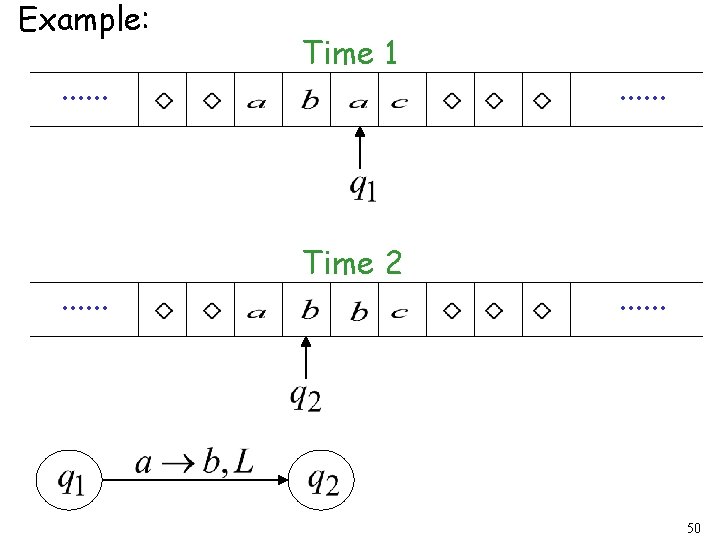
. . . Time 1 Time 2 . . . 49

Example: . . . Time 1 Time 2 . . . 50

Example: . . . Time 1 Time 2 . . . 51

Determinism Turing Machines are deterministic Allowed Not Allowed No lambda transitions allowed 52

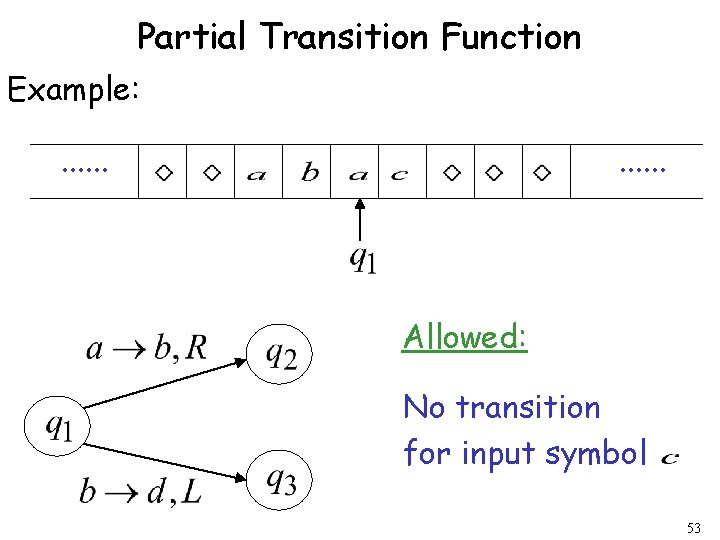
Partial Transition Function Example: . . . Allowed: No transition for input symbol 53

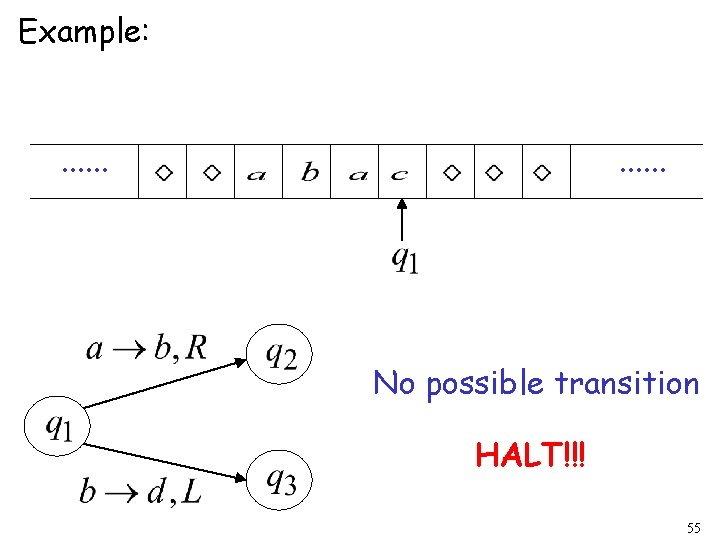
Halting The machine halts if there are no possible transitions to follow 54

Example: . . . No possible transition HALT!!! 55

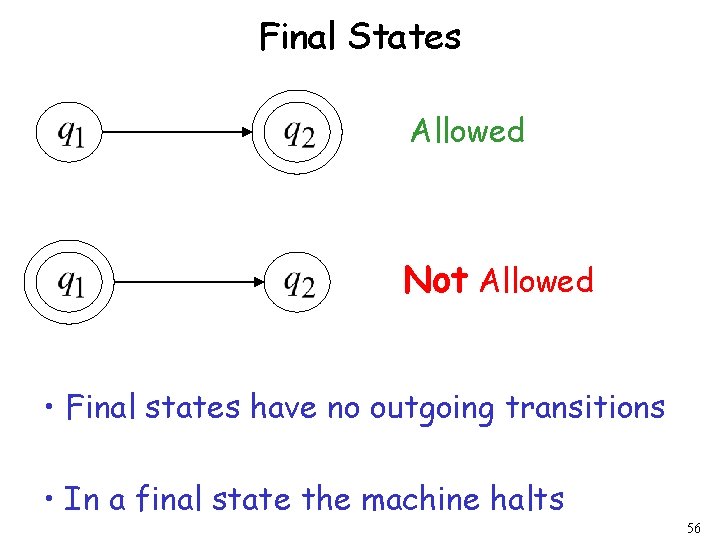
Final States Allowed Not Allowed • Final states have no outgoing transitions • In a final state the machine halts 56

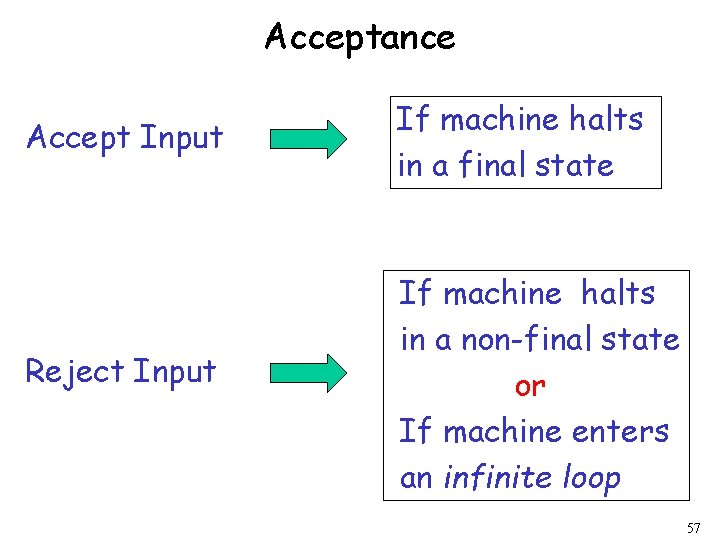
Acceptance Accept Input If machine halts in a final state Reject Input If machine halts in a non-final state or If machine enters an infinite loop 57

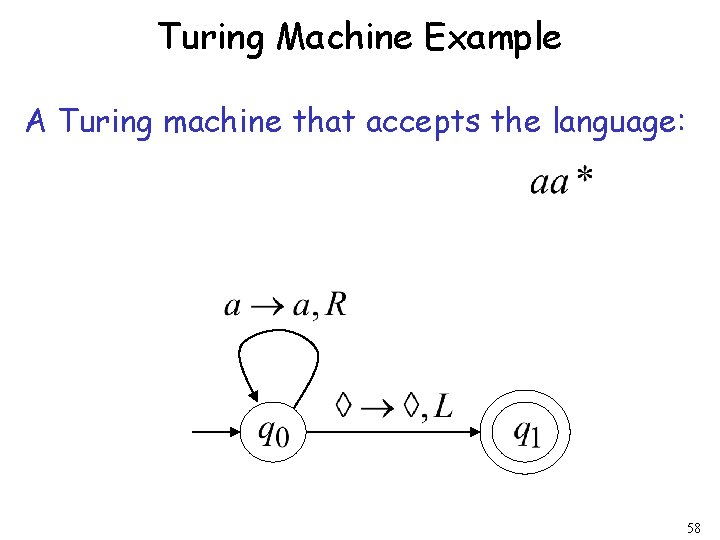
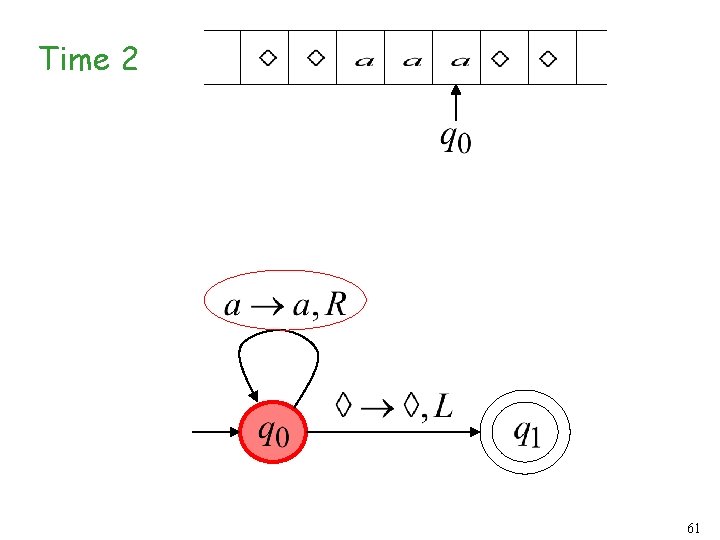
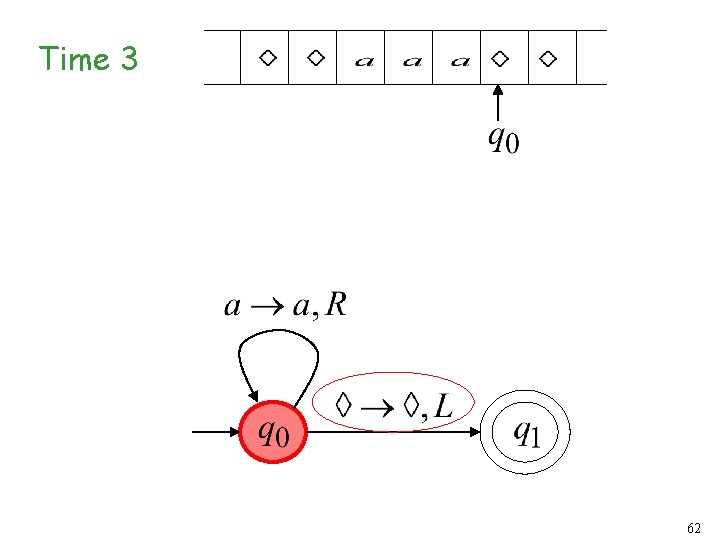
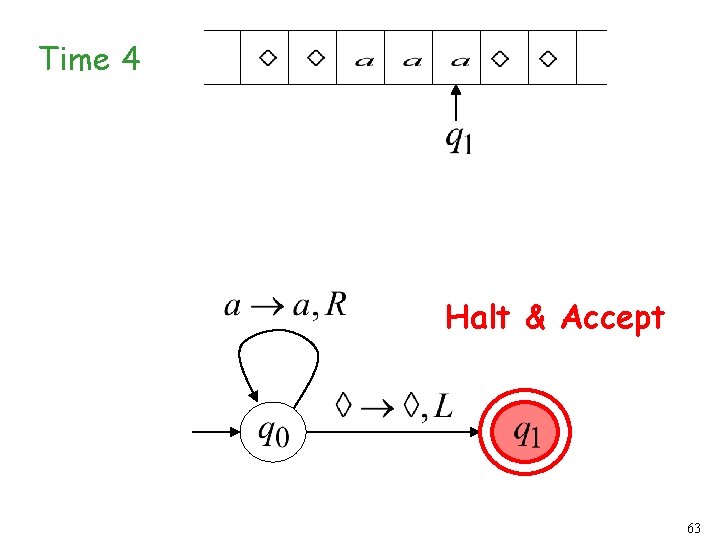
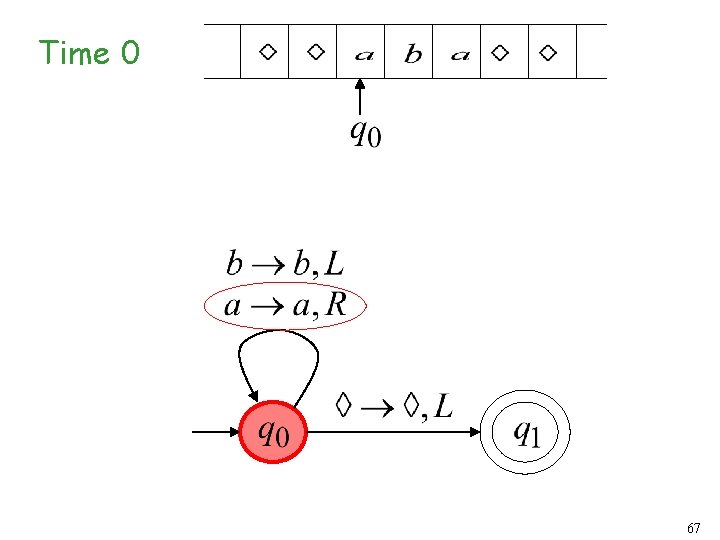
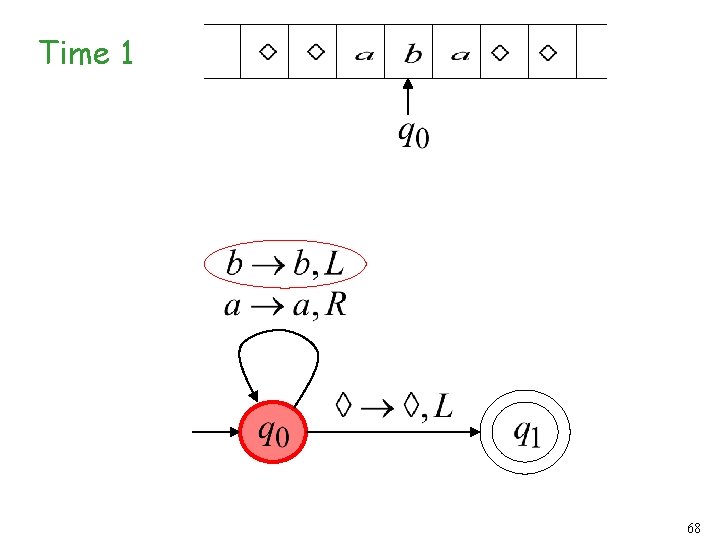
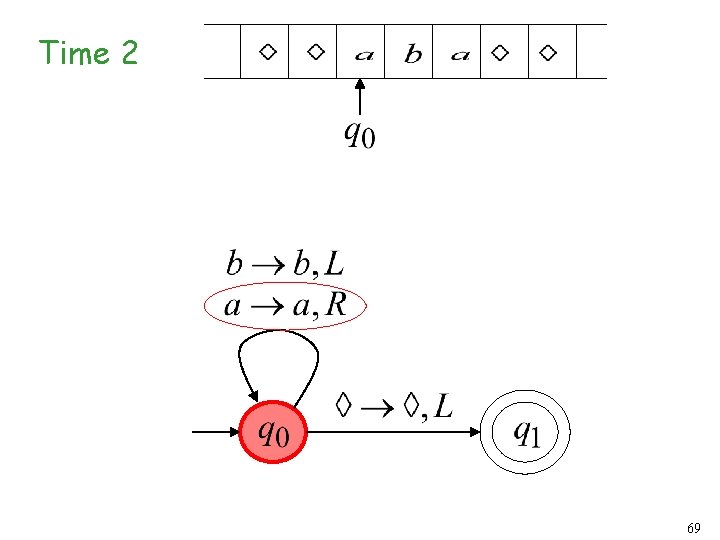
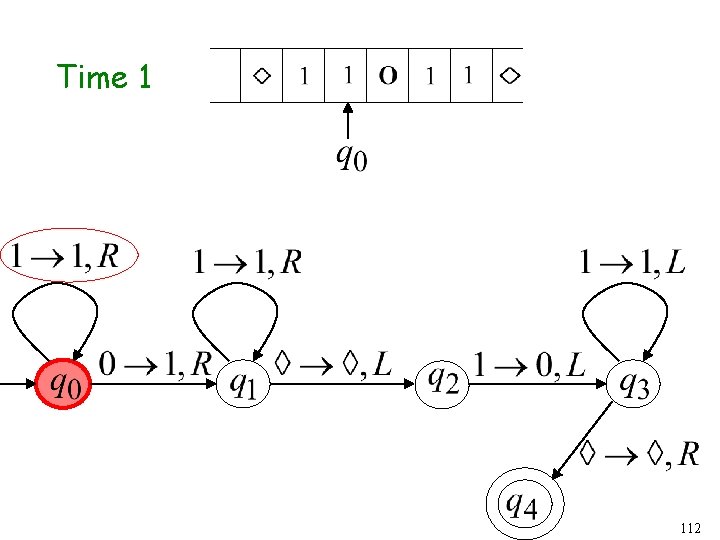
Turing Machine Example A Turing machine that accepts the language: 58

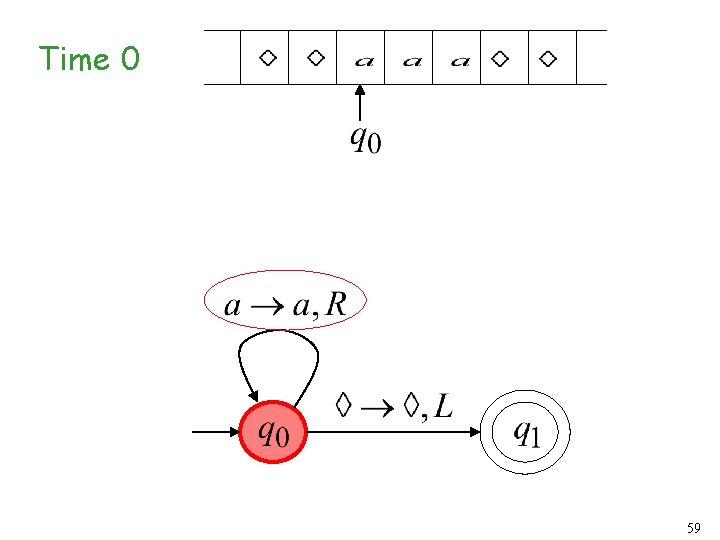
Time 0 59

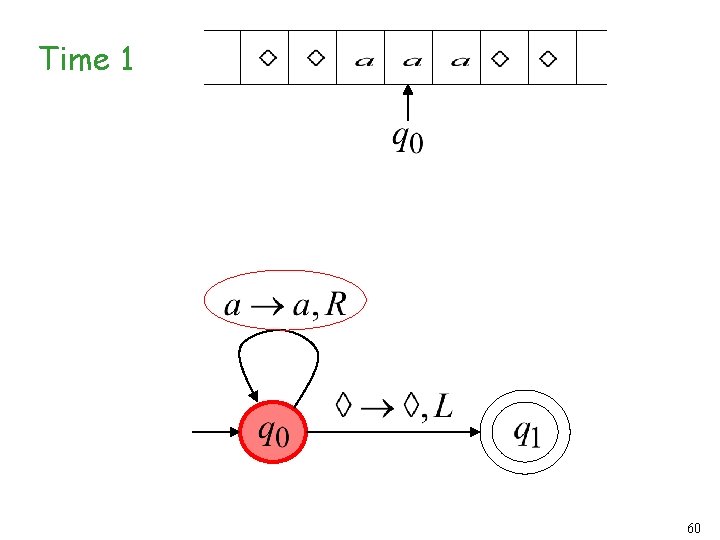
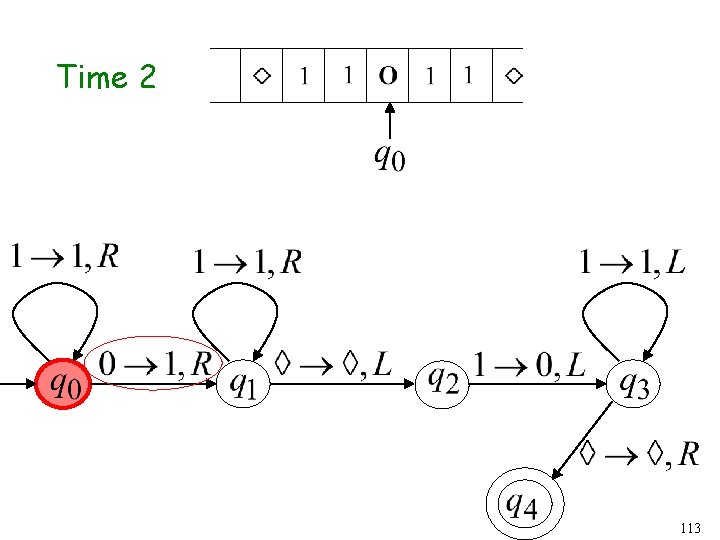
Time 1 60

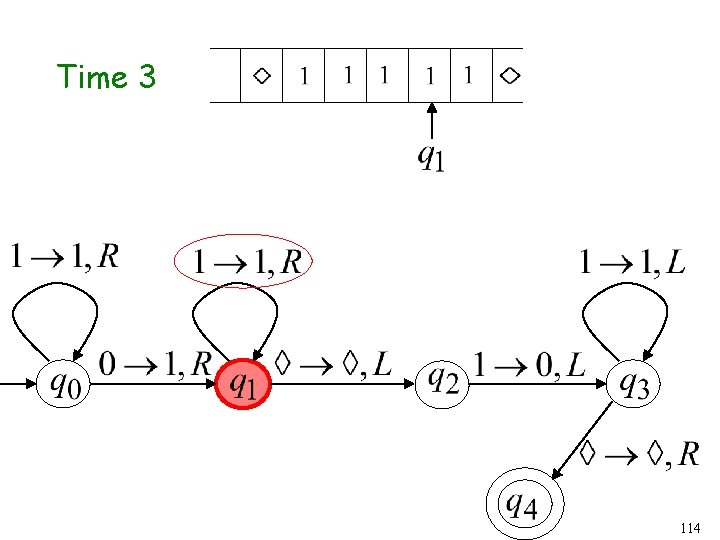
Time 2 61

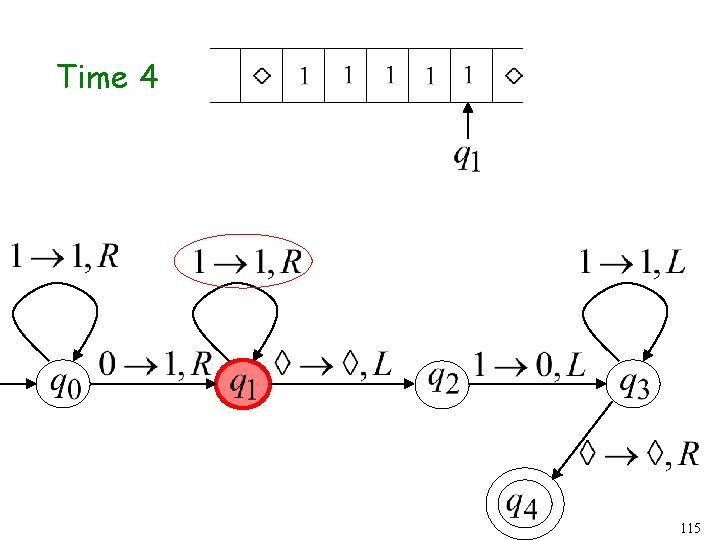
Time 3 62

Time 4 Halt & Accept 63

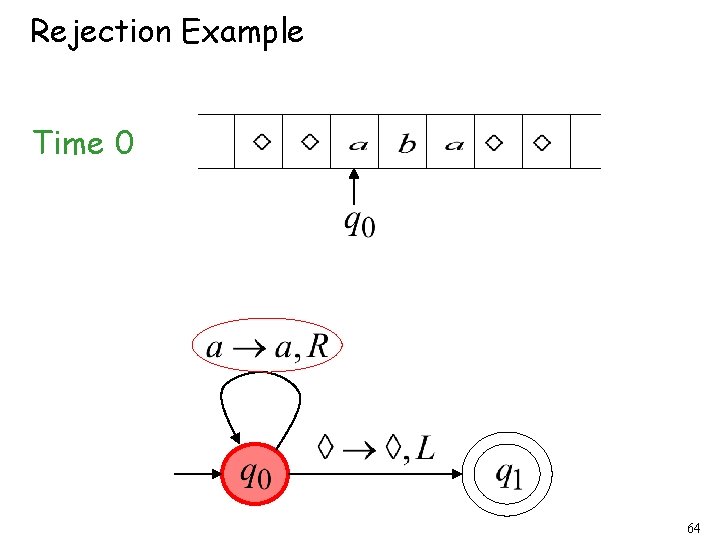
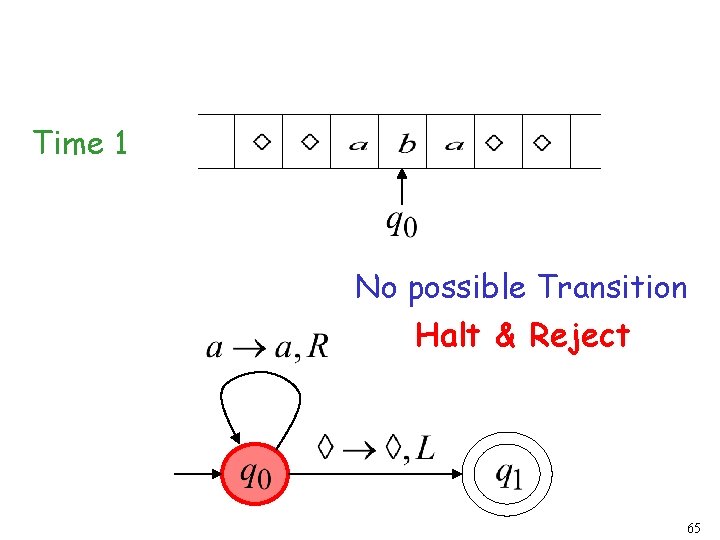
Rejection Example Time 0 64

Time 1 No possible Transition Halt & Reject 65

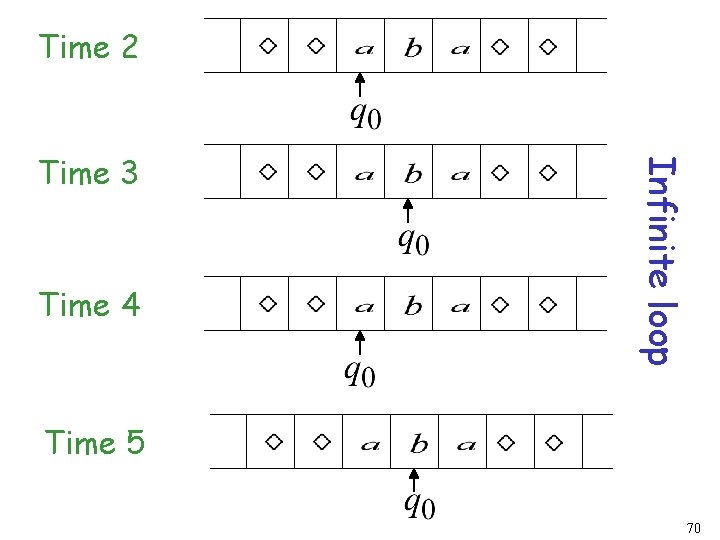
Infinite Loop Example A Turing machine for language 66

Time 0 67

Time 1 68

Time 2 69

Time 2 Time 4 Infinite loop Time 3 Time 5 70

Because of the infinite loop: • The final state cannot be reached • The machine never halts • The input is not accepted 71

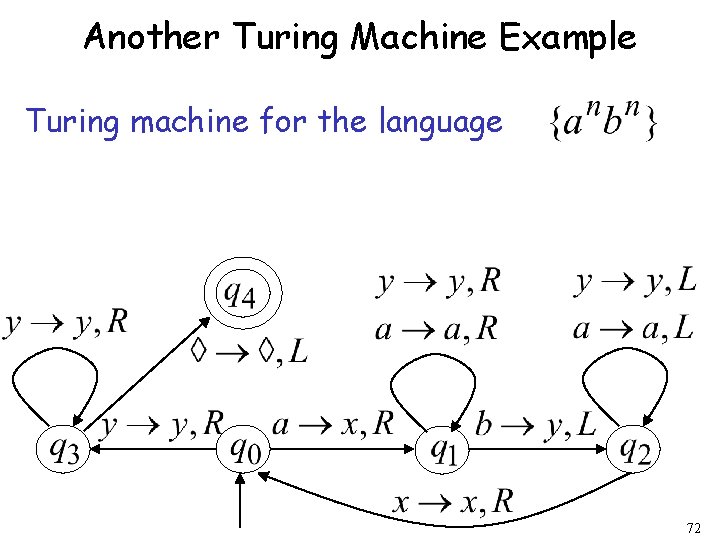
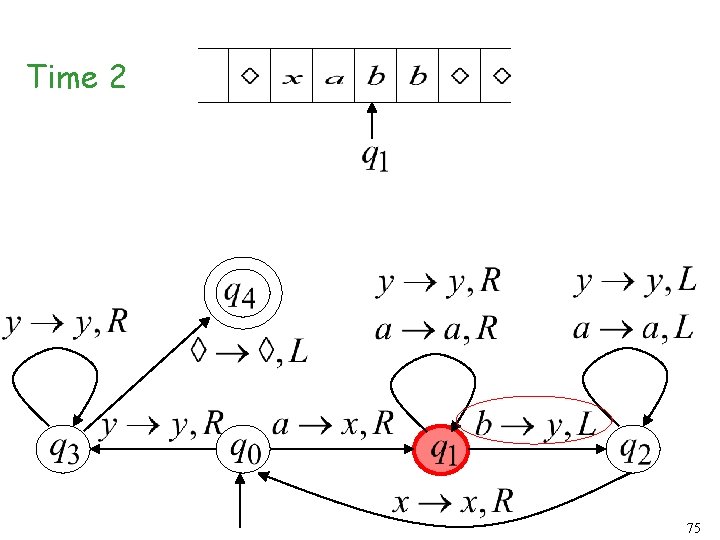
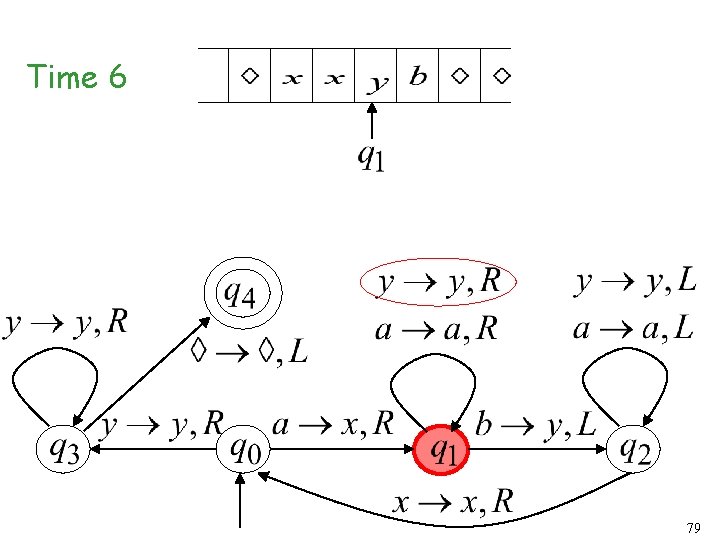
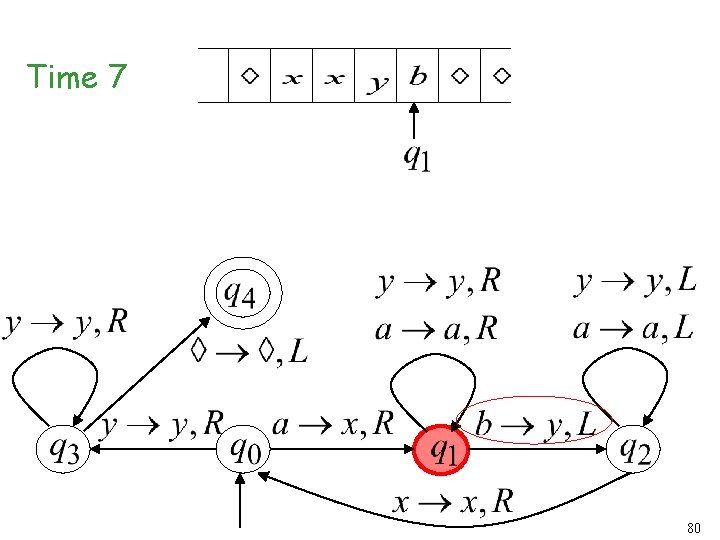
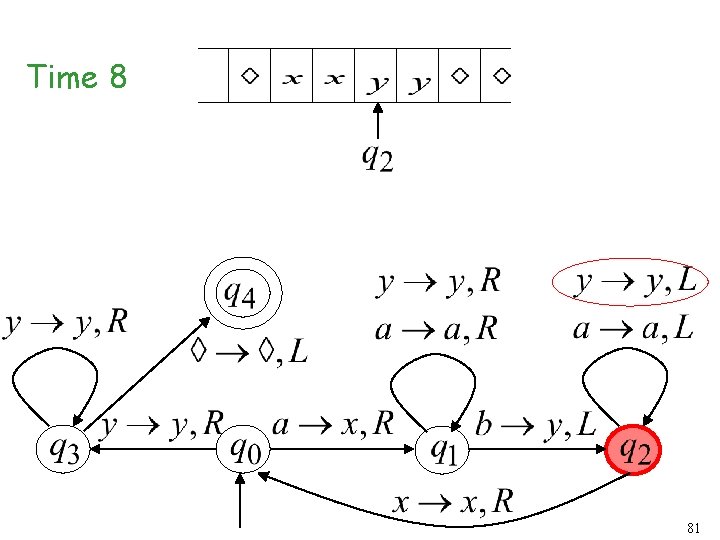
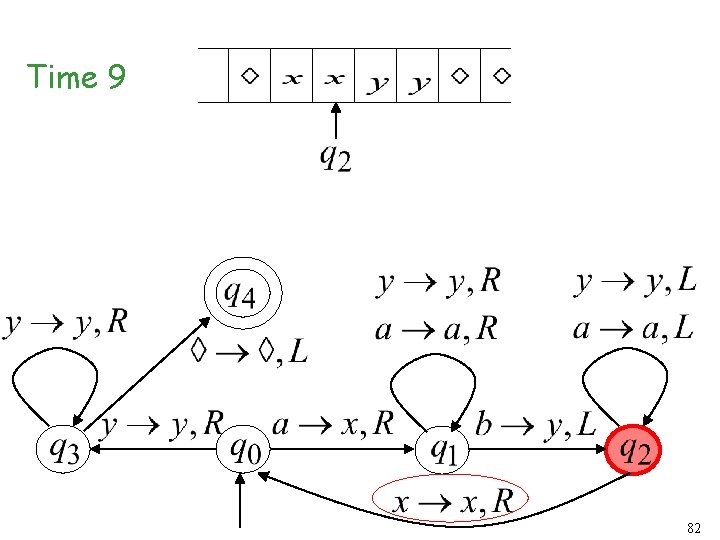
Another Turing Machine Example Turing machine for the language 72

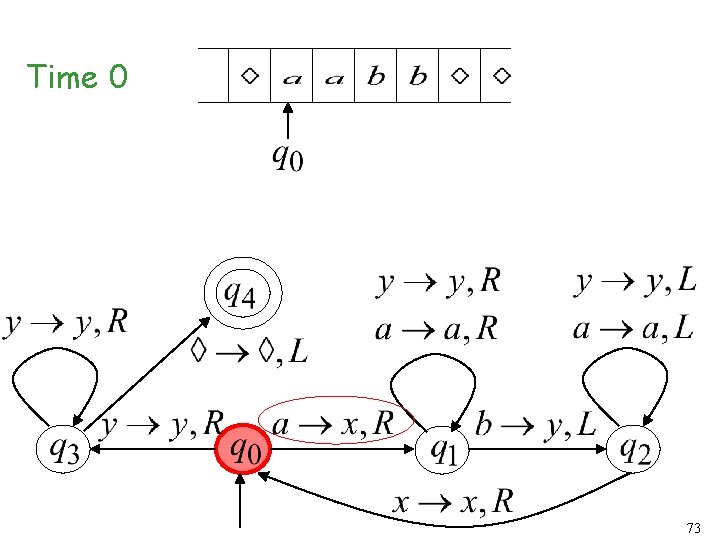
Time 0 73

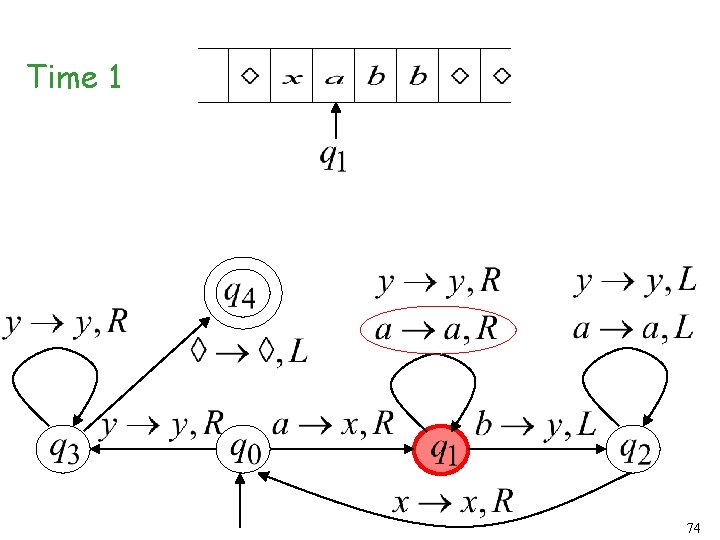
Time 1 74

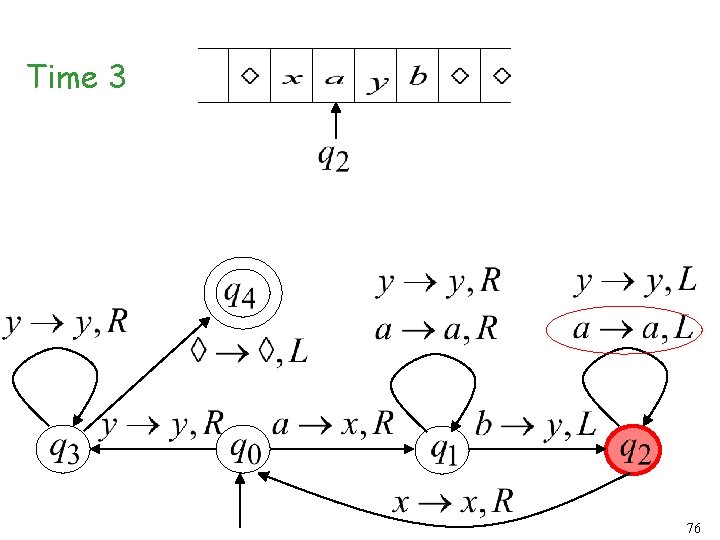
Time 2 75

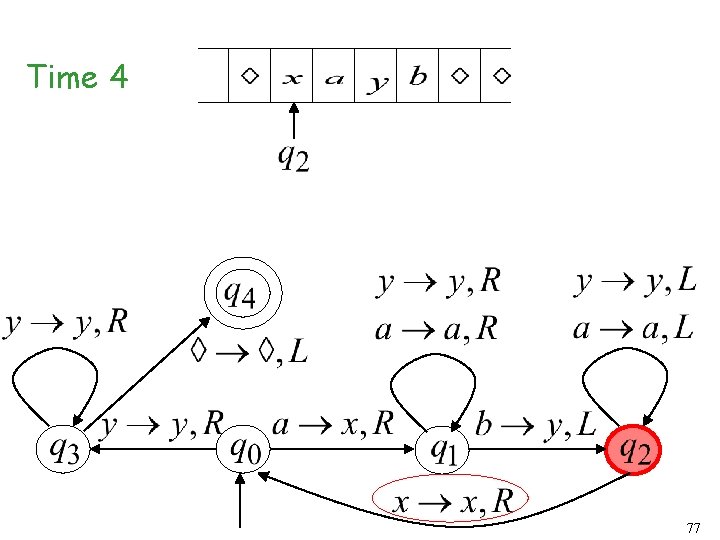
Time 3 76

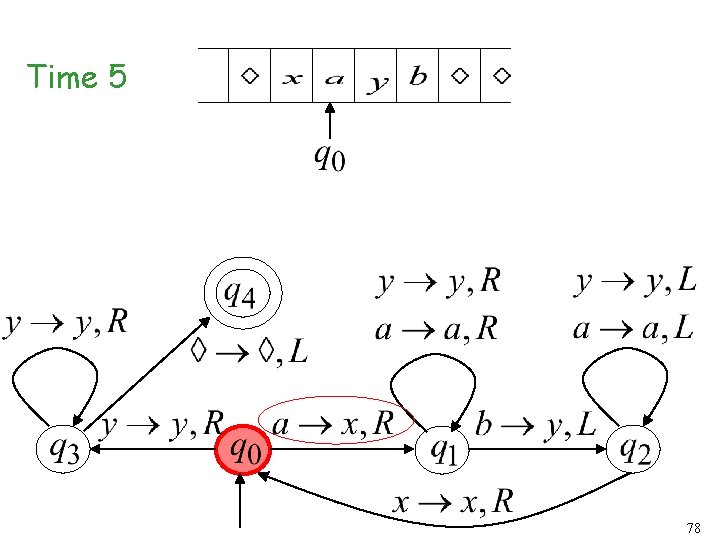
Time 4 77

Time 5 78

Time 6 79

Time 7 80

Time 8 81

Time 9 82

Time 10 83

Time 11 84

Time 12 85

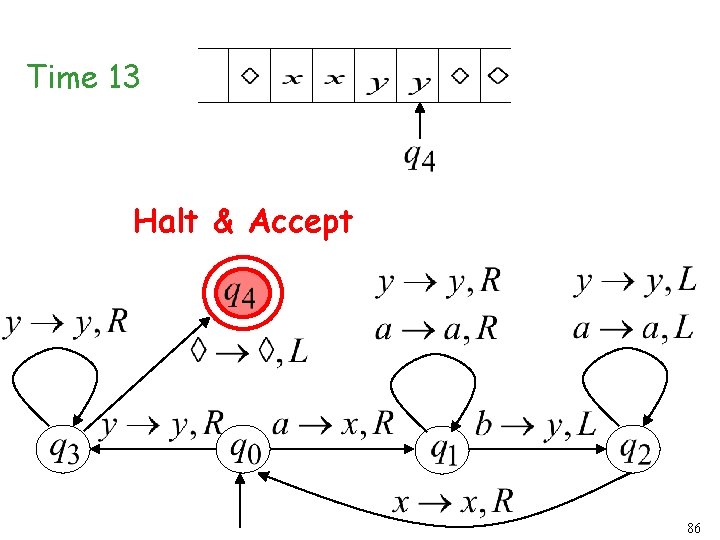
Time 13 Halt & Accept 86

Observation: If we modify the machine for the language we can easily construct a machine for the language 87

Formal Definitions for Turing Machines 88

Transition Function 89

Transition Function 90

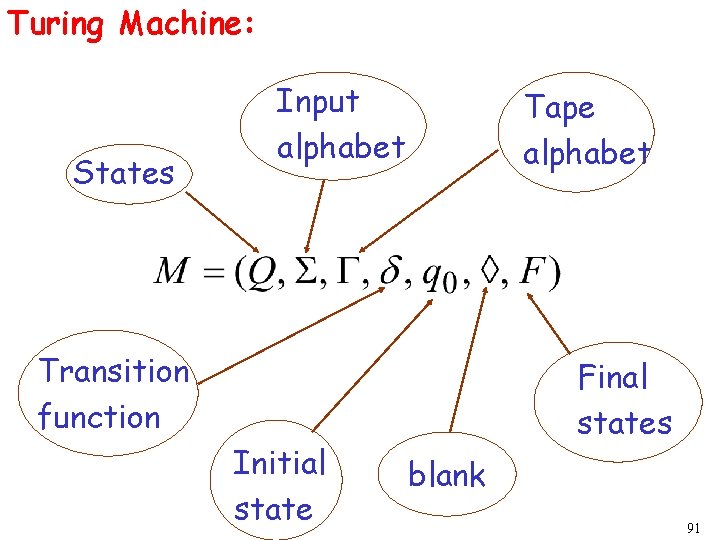
Turing Machine: States Input alphabet Tape alphabet Transition function Initial state Final states blank 91

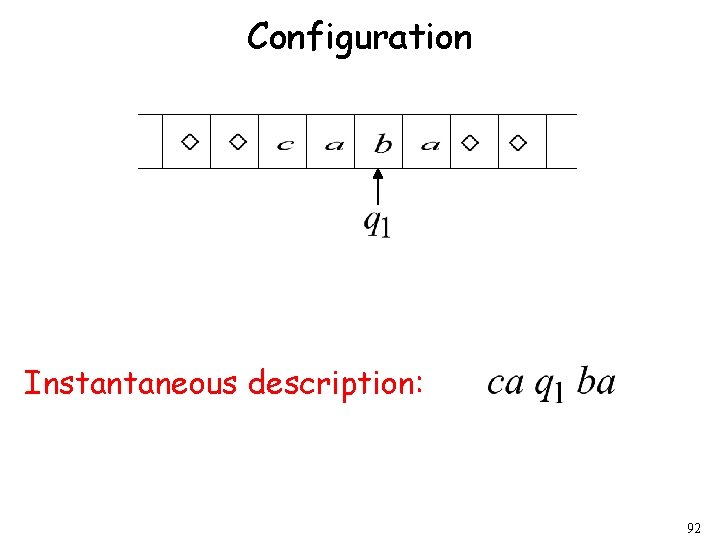
Configuration Instantaneous description: 92

Time 4 Time 5 A Move: 93
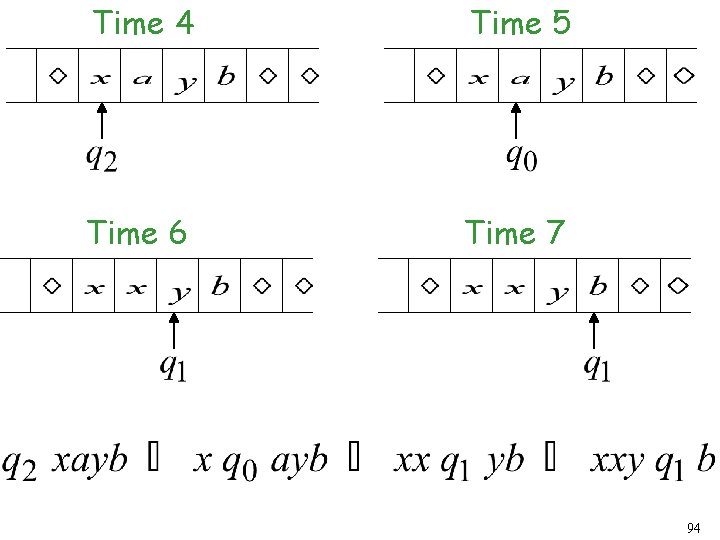
Time 4 Time 5 Time 6 Time 7 94

Equivalent notation: 95

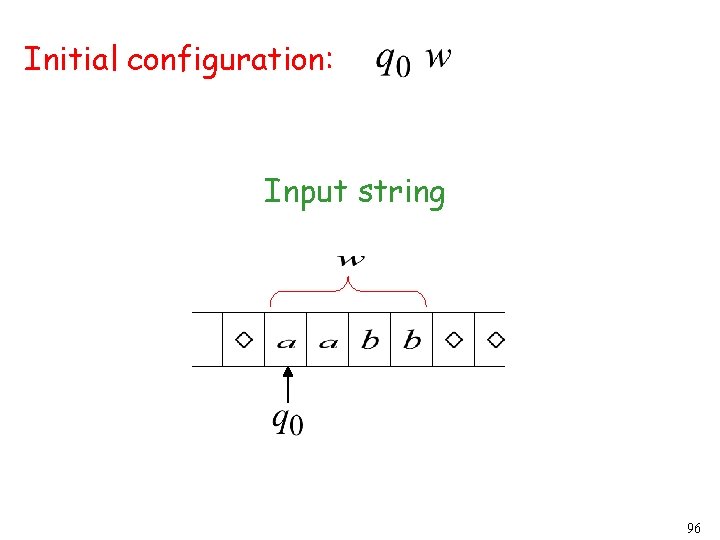
Initial configuration: Input string 96

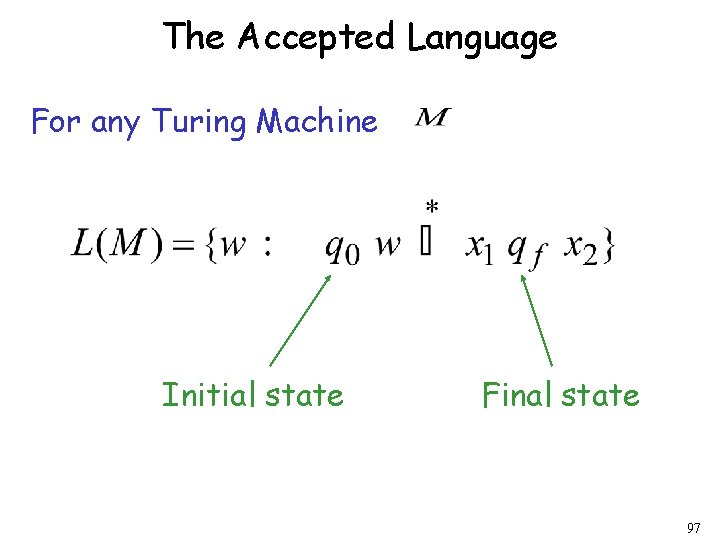
The Accepted Language For any Turing Machine Initial state Final state 97

Standard Turing Machine The machine we described is the standard: • Deterministic • Infinite tape in both directions • Tape is the input/output file 98

Computing Functions with Turing Machines 99

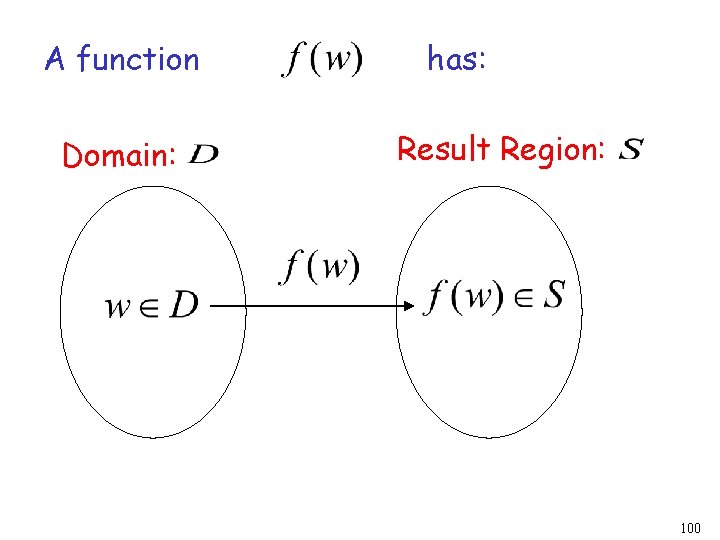
A function Domain: has: Result Region: 100

A function may have many parameters: Example: Addition function 101

Integer Domain Decimal: 5 Binary: 101 Unary: 11111 We prefer unary representation: easier to manipulate with Turing machines 102

Definition: A function is computable if there is a Turing Machine such that: Initial configuration Final configuration initial state For all final state Domain 103

In other words: A function is computable if there is a Turing Machine such that: Initial Configuration For all Final Configuration Domain 104

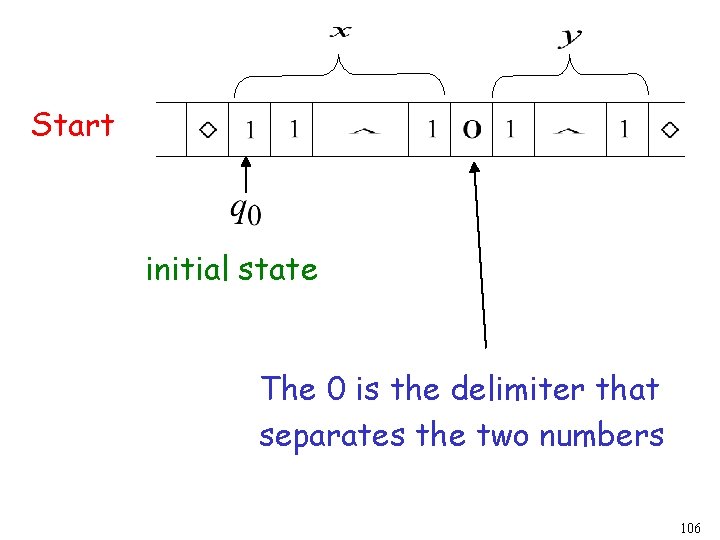
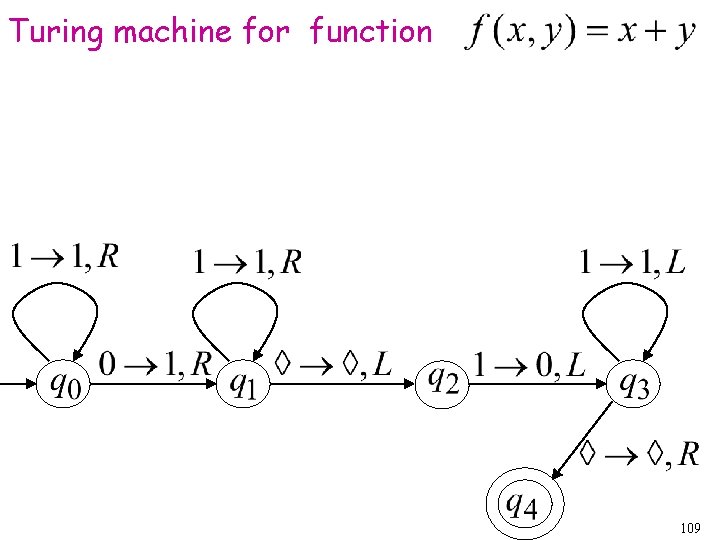
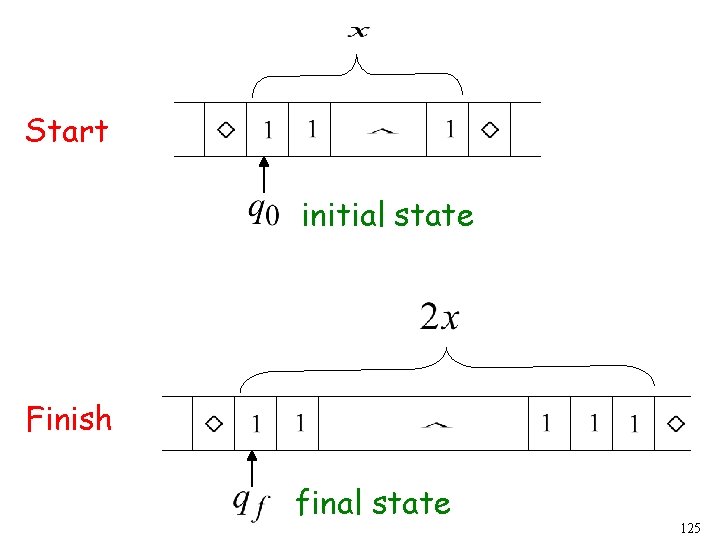
Example The function is computable are integers Turing Machine: Input string: unary Output string: unary 105

Start initial state The 0 is the delimiter that separates the two numbers 106

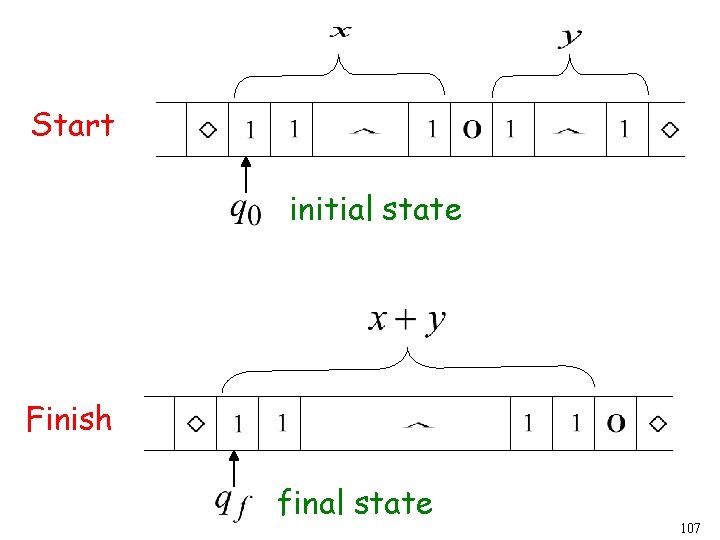
Start initial state Finish final state 107

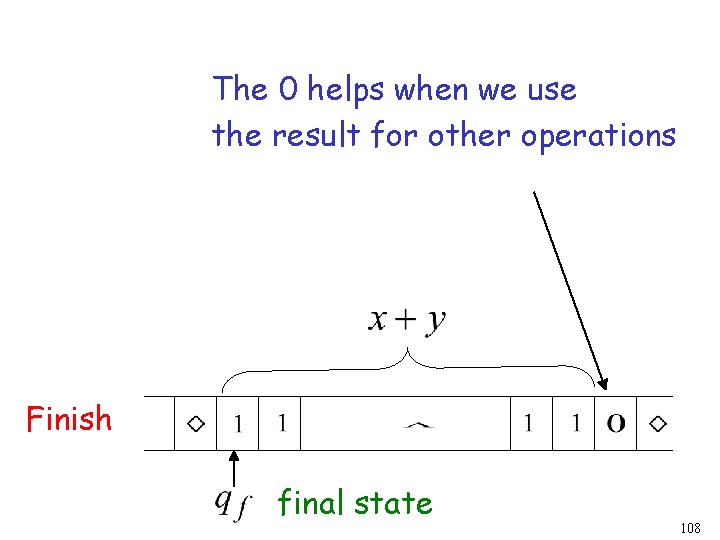
The 0 helps when we use the result for other operations Finish final state 108

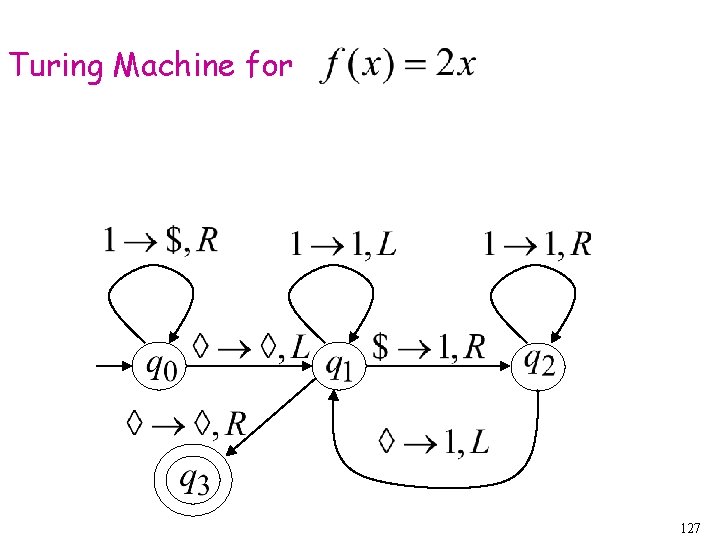
Turing machine for function 109

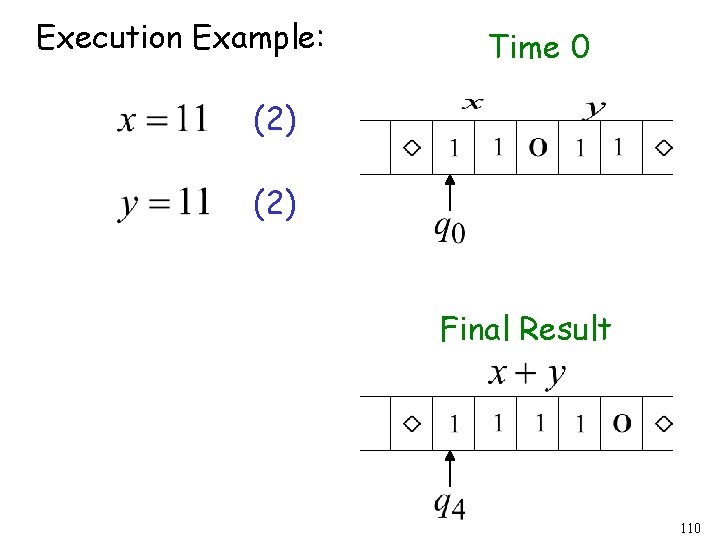
Execution Example: Time 0 (2) Final Result 110

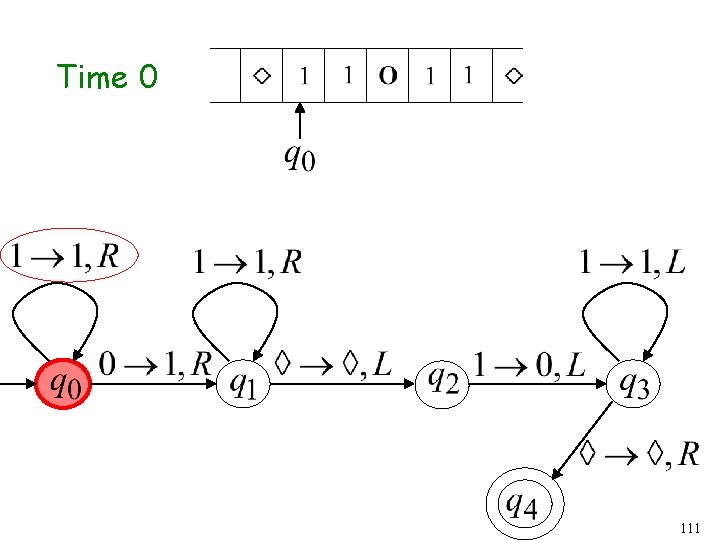
Time 0 111

Time 1 112

Time 2 113

Time 3 114

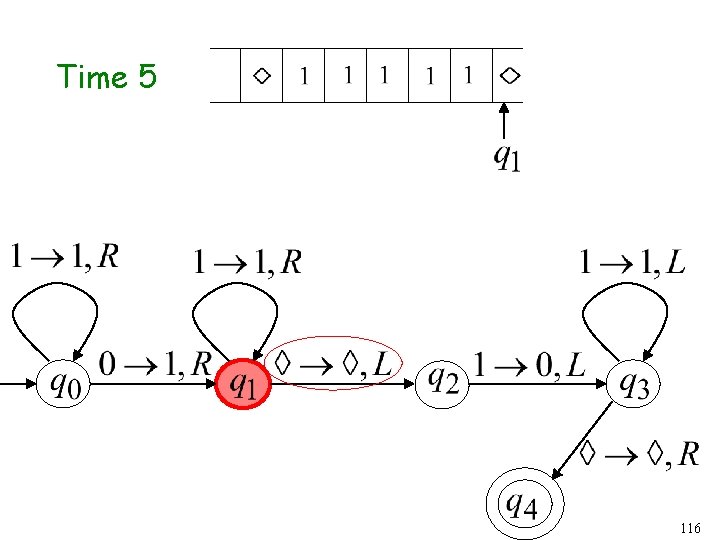
Time 4 115

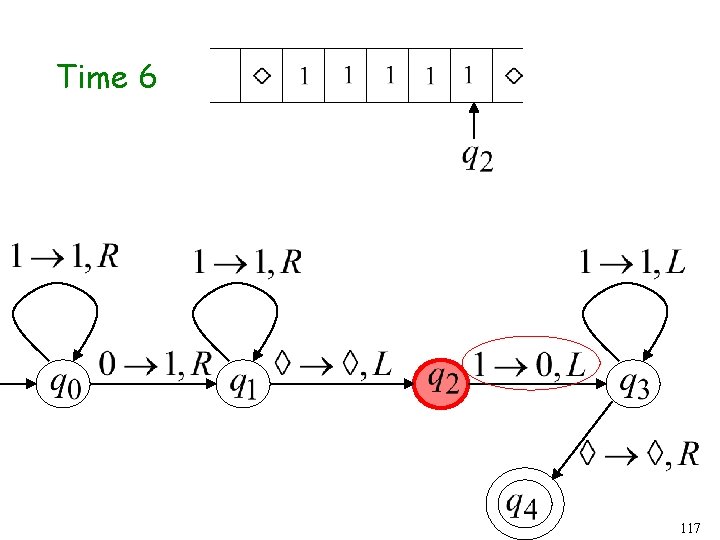
Time 5 116

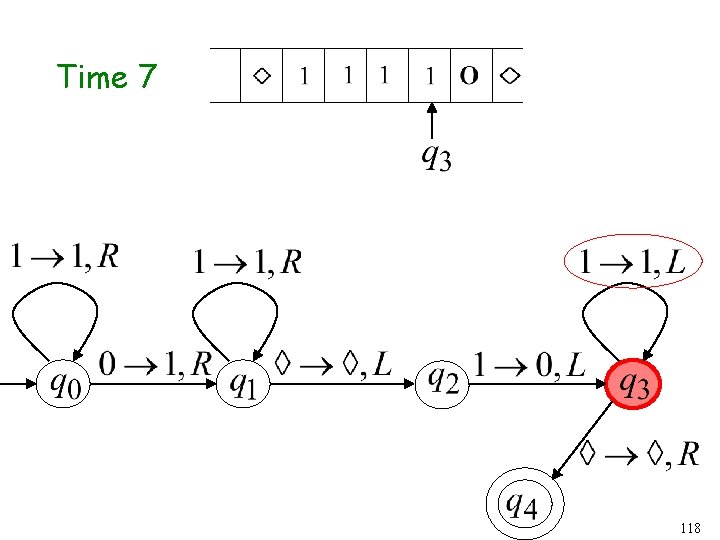
Time 6 117

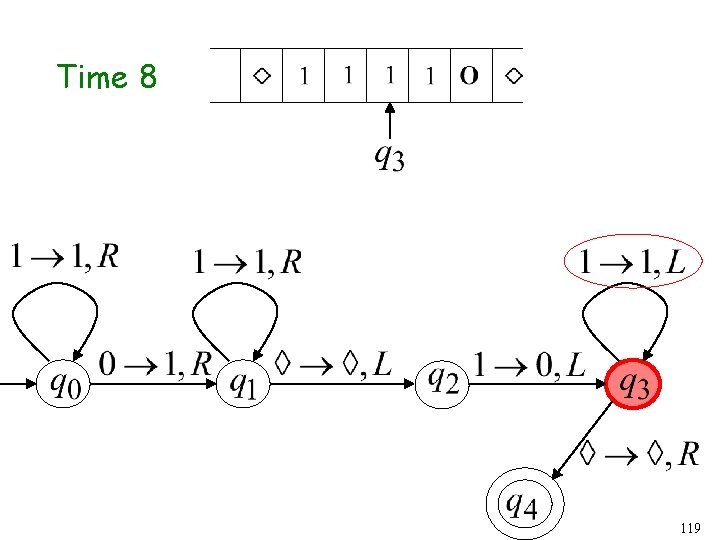
Time 7 118

Time 8 119

Time 9 120

Time 10 121

Time 11 122

Time 12 HALT & accept 123

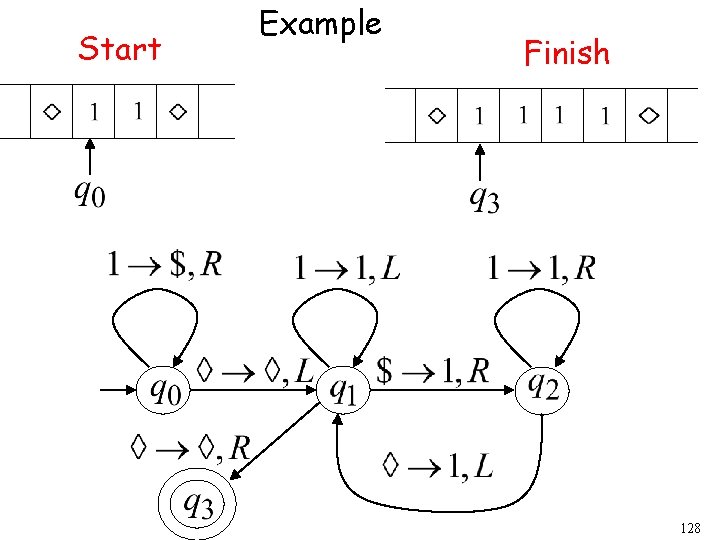
Another Example The function is computable is integer Turing Machine: Input string: unary Output string: unary 124

Start initial state Finish final state 125

Turing Machine Pseudocode for • Replace every 1 with $ • Repeat: • Find rightmost $, replace it with 1 • Go to right end, insert 1 Until no more $ remain 126

Turing Machine for 127

Start Example Finish 128

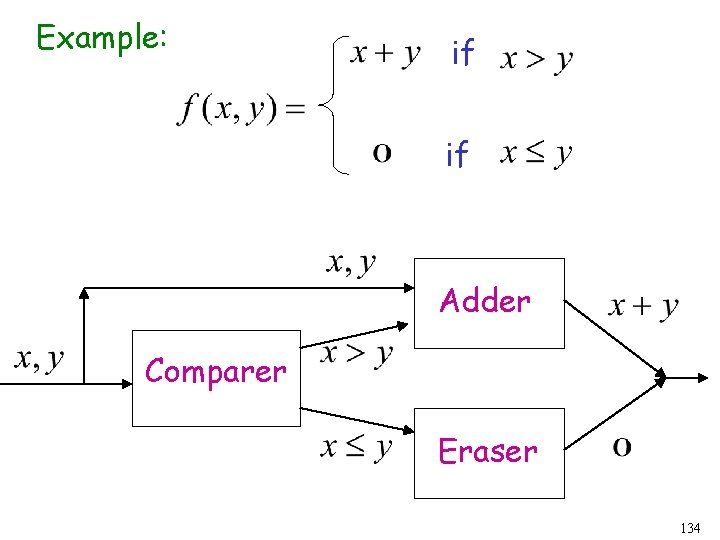
Another Example if The function is computable if 129

Turing Machine for if if Input: Output: or 130

Turing Machine Pseudocode: • Repeat Match a 1 from Until all of or with a 1 from is matched • If a 1 from is not matched erase tape, write 1 else erase tape, write 0 131

Combining Turing Machines 132

Block Diagram input Turing Machine output 133

Example: if if Adder Comparer Eraser 134