Turing Machines A more powerful computation model than

Turing Machines A more powerful computation model than a PDA ? [Section 9. 1]

Turing Machines [Section 9. 1] Some history: - introduced by Alan Turing in 1936 - models a “human computer” (human writes/rewrites symbols on a sheet of paper, the human’s state of mind changes based on what s/he has seen) - a reasonable model for real computers Church-Turing Thesis: For any problem L (given by a language) there exists an algorithm iff there exists a Turing machine which terminates on every input.

Real-world problems vs. languages [Section 9. 1] Example : the airline problem - given are airports and available flights, is it possible to get from a place A to a place B ?

Turing Machines cont. [Section 9. 1] Verbal explanation: - The tape is infinite to the right and it initially contains the input string (the rest of the tape contains blanks - M). - The TM starts in an initial state, reading the first symbol on the tape. - The head can move left, right, or stay at its current position. - The TM has two special states, ha (accept) and hr (reject). - If the head moves to the left of the first symbol, this automatically means the change of state to hr (reject). - The transition is specified by a state and a tape symbol (to which the head points). It returns a new state, new tape symbol (to rewrite the original), and a head-move (L/R/S).

Turing Machines cont. [Section 9. 1] Example : As a warm-up, give a Turing machine for a*b*c* Simplified transition diagram : do not have to draw transitions leading to hr. we

Turing Machines cont. [Section 9. 1] A Turing machine (TM) is a 5 -tuple (Q, , , q 0, ) where - Q is a finite set of states not containing ha, hr (the two halting states) - is a finite alphabet (input symbols) - is a finite alphabet (tape symbols) such that µ and does not contain M (the blank symbol) - qo 2 Q is the initial state - : ____________ is a partial function defining the transitions

Turing Machines cont. [Section 9. 1] Let T = (Q, , , q 0, ) be a TM. A configuration of T is ________. The initial configuration is ________. We use `T to say that T can get from one configuration to another configuration using a single transition. We use `T* to say that T can get from one configuration to another configuration using a sequence of transitions.

Turing Machines cont. [Section 9. 1] Let T = (Q, , , q 0, ) be a TM and x 2 *. We say that x is accepted by T if ___________. The language accepted by T, denoted L(T), is the set of all strings in * that are accepted by T. A string x can be rejected in two ways : either the computation of T on x ends in the state hr, or the computation of T on x gets into an infinite loop. A language accepted by a TM is called recursively enumerable. A language for which there is a TM which never goes to an infinite loop is called recursive.

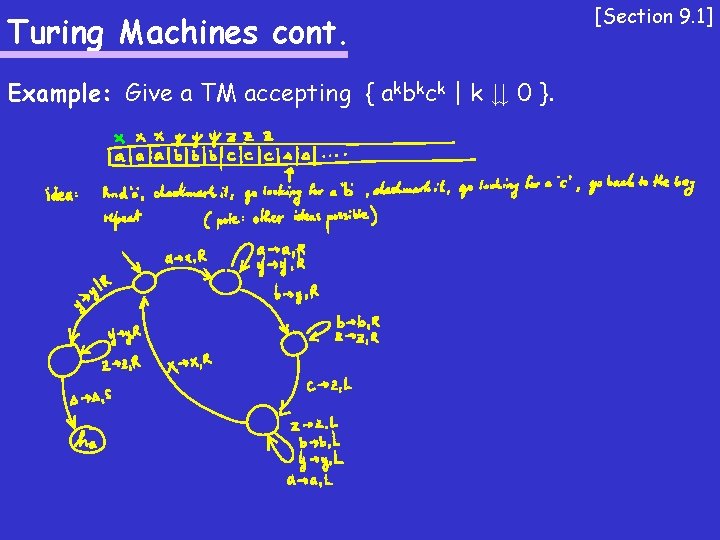
Turing Machines cont. Example: Give a TM accepting { akbkck | k ¸ 0 }. [Section 9. 1]

Turing Machines and functions [Section 9. 2] Let T = (Q, , , q 0, ) be a TM and let f be a total function from * to *. We say that T computes f if for every x 2 *, (q 0, Mx) `T* (ha, Mf(x)). Example : give a TM that computes the function f(1 n) = 12 n

A stronger machine than a TM ? [Section 9. 4] Possible attempts to make Turing machines stronger : - 2 -way infinite tape - several heads, several tapes - random access (the head can jump to any position) - nondeterminism - etc. Note: All of the above changes can be simulated by a TM.

A stronger machine than a TM ? [Section 9. 4] Example : How to simulate a 2 -way infinite tape using a regular TM ?

Nondeterministic TM (NTM) [Section 9. 5] The definition is the same as Turing machines, except that the transition function goes from Q £ ( [ {M}) to subsets of (Q [ {ha, hr}) £ ( [ {M}) £ {R, L, S}. Thm : Let T 1 be an NTM. Then there exist a TM T 2 such that L(T 1)=L(T 2).