Interaction Machines Are they more powerful than Turing

Interaction Machines Are they more powerful than Turing Machines? T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

Today's Presentation T. Gregory Bandy ● A New Paradigm ● Turing Machines ● Interaction Machines ● Understanding the Issues ● Extending Turing Machines ● Observations ● Questions Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

A New Paradigm ● ● ● Peter Wegner 1997 - Interaction Machines are a more powerful class of computability than Turing Machines. More powerful than algorithms. Interaction with the external world and responding to new inputs. Not inductive. T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

An Interaction Machine? T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

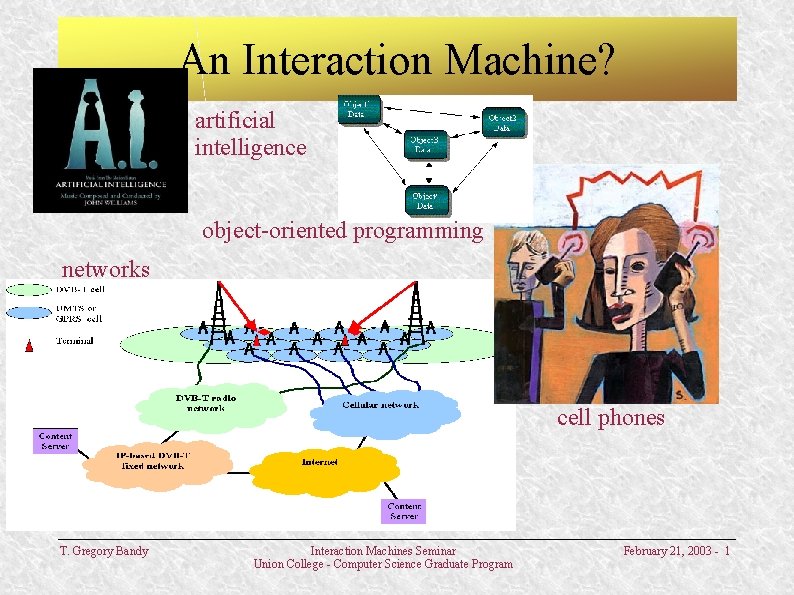
An Interaction Machine? artificial intelligence object-oriented programming networks cell phones T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

Turing Machine ● Alan Turing (1912 -1954) ● The Standard Turing Machine The Turing Machine has an input-output tape that is infinite in both directions and allows an infinite number of left and right moves. Commands: ● Read tape ● Move tape left ● Move tape right ● Write 0 on tape ● Write 1 on tape ● Jump to another command ● Halt T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

Turing Machine ● The Standard Turing Machine – TM starts with all input already on tape. Finite amount of input. – TM result written to tape when TM halts. – State transitions specified when / before TM starts. – Deterministic or Nondeterministic. – TM's may be combined. – Halting is important. T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

Turing Machine ● Standard Turing Machine variations – Semi-infinite tape – Off-line input – Multi-tape – Multi-dimensional tape T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

Turing Machine ● The Universal Turing Machine Can simulate any other TM. – Multi-tape TM with 3 tapes ● Description of other TM. ● Other TM's tape. ● Other TM's internal state during execution. – A reprogrammable TM. – UTM designed with 2 state and 7 colors. – T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

Turing Machine History ● ● Alonzo Church (1903 -1995) - recursive functions define 'computability. ' Church Kurt Gödel (1906 -1978) - reached similar conclusion. Alan Turing - demonstrated TM's compute recursive functions. S. C. Kleene, et. al - recognized 'effective methods' must be recursive. Kleene Post Gödel T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

Interaction Machine Turing machines extended by adding input and output actions that support dynamic interaction with an external environment are called interaction machines. T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

Interaction Claims ● ● ● Interaction is not expressible by algorithms. Interaction Machines cannot be modeled by Turing Machines. Interaction is more powerful than algorithms. Interaction cannot be specified by first-order logic or state-transition semantics. Interaction permits computing that is not algorithmically describable. T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

Interaction Machine ● A Turing Machine, extended. . . – initial input is not fully defined – input and output are streams, not strings – specified by interaction histories, rather than algorithms – receives external input during execution – output remembered between executions – no halting state T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

Interaction Streams ● ● Streams are – dynamic - not fixed in advance – evolving - changing independent of the IM – partial structures - not defined in advance – may depend on time, adversaries, oracles, and protocols of interaction - again, changing independent of the IM Streams may be produced by multiple unspecified IMs T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

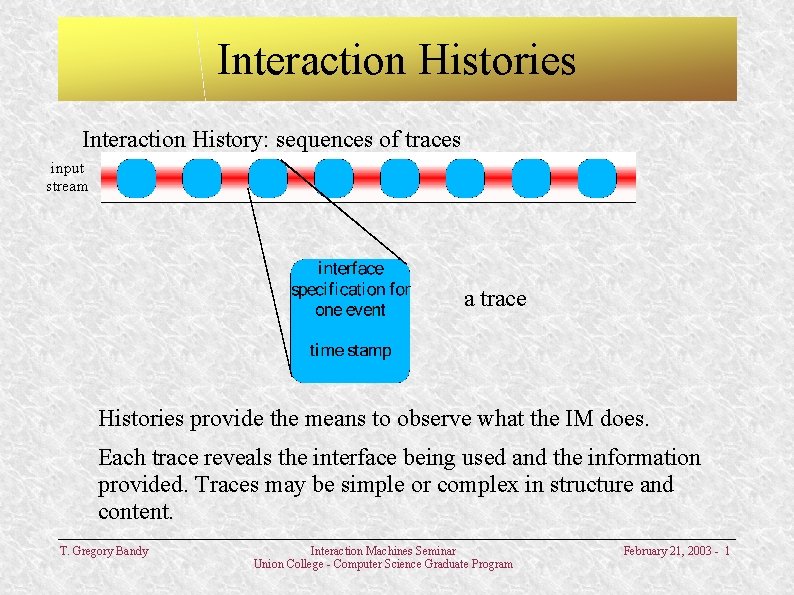
Interaction Histories Interaction History: sequences of traces input stream a trace Histories provide the means to observe what the IM does. Each trace reveals the interface being used and the information provided. Traces may be simple or complex in structure and content. T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

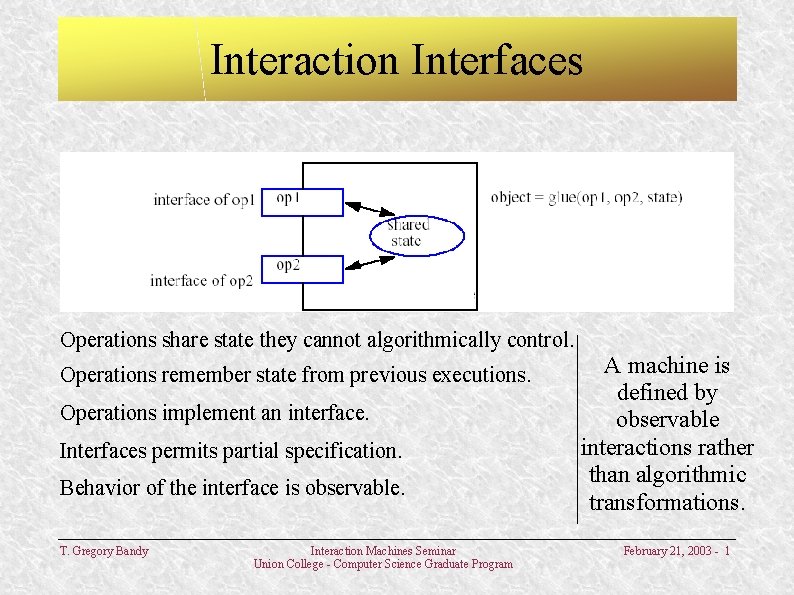
Interaction Interfaces Operations share state they cannot algorithmically control. Operations remember state from previous executions. Operations implement an interface. Interfaces permits partial specification. Behavior of the interface is observable. T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program A machine is defined by observable interactions rather than algorithmic transformations. February 21, 2003 - 1

Understanding the Issues T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

Understanding the Issues Computability Classic Computability – all inputs to an algorithm yield a valid result. – effective computability yields the result in finite steps and with no outside help – measured by classes of complexity Interactive Computation – provides a service over time. – values of inputs and outputs are interdependent – measured by expressiveness T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

Understanding the Issues Church-Turing Thesis Classic CT equates the effective computability of functions and algorithms with Turing Machines. – This maps the intuitive notion of computability by algorithms to the formal notion of Turing Machines. – The TM formal model dominates. Interaction CT would correlate interactive computing with coinductive models of computing using coalgebras. – This maps the formal notion of coinduction to the intuitive notion of interactive computing. – The interactive computing notion dominates. T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

Understanding the Issues Powerfulness Classic Powerfulness – Power means the ability to solve more complex classes of problems. I. e. , computational limits. – Push-Down Automata (PDA) are more powerful or expressive than Finite State Automata (FSA). Interaction Expressiveness – the ability of observers to make observational distinctions. – observations permit evaluating algorithms and interactions. – better way to reason about a process (Milner) Milner T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

Understanding the Issues Mathematics & Logic Classic computability theory is dominated by First. Order Logic. – basic to algorithms and computability theory – shown to be incomplete. – uses least-fixpoint semantics Interactive computation is expressed using coinduction, coalgebras, and bisimulation. – accommodates incompleteness. – coalgebras define steps of observation – uses greatest-fixpoint semantics in logic which permit operating on infinite input streams. T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program Goldin February 21, 2003 - 1

Extending Turing Machines Persistent Turing Machine The PTM is a perpetual nondeterministic Turing Machine with 3 tapes that continuously reads input, computes, and outputs results. Goldin Smolka Wegner – Extends the existing nondeterministic 3 tape TM (N 3 TM) ( ≡ Standard single tape TM). – The work tape captures the N 3 TM state and persists between computations for later use. – The input and output are a coinductively defined pair (win, wout) that define the computation performed. – Infinite sequences of pairs that get their source from and produce output to an external environment. T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

Extending Turing Machines Interactive Turing Machine with Advice The ITMA extends the Turing Machine with advice, with infinite computations, and accommodates interaction. van Leeuwen Wiedermann – Infinite computations and interaction are existing TM extensions. – Advice is a noncomputable alteration that affects and improved the computing capability. – Turing proposed choice machines as well as automated machines that we know as TMs. T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

Observations ● ● ● Excellent testimony for the value of academia. Vigorous discussions, critiques, and rebuttals. Interaction is widely observed, but is hard to formalize. Co- mathematics hold promise. Interaction appeals to the intuitive notion that not all computing is algorithmic. Confusion of terms hamper evaluating IMs. Unclear whether IMs are indeed more powerful than TMs. T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1

Questions ● ● ● Can IMs be thought of as sophisticated combinable TMs? Can the relative power of algorithms and coinduction be evaluated in terms of their observational behavior? How far can TMs be legitimately extended? Does IM theory deserve being taught along with automata theory? Union College's Mathematics Department course listing does not appear to teach coinduction, coalgebra, or bisimulation. Should such courses be offered? T. Gregory Bandy Interaction Machines Seminar Union College - Computer Science Graduate Program February 21, 2003 - 1