Comparing Fractions Greater Than Less Than or Equal






- Slides: 9

Comparing Fractions Greater Than, Less Than, or Equal To?

Review Our Learning Goals: For fractions with denominators 2, 3, 4, 5, 6, 8, 10, 12, and 100— I can: v Use a visual fraction model to explain why you can multiply the numerator and denominator of a fraction by the same number to make an equivalent fraction v Recognize that I can only compare fractions when they refer to the same size whole. Ø Compare two fractions with different numerators and different denominators using different strategies (e. g. , by creating common denominators or numerators, and comparing to a benchmark fraction such as 1/ 2. ) Ø Compare fraction using >, =, <; justify the comparison by using a visual fraction model

Finding Equivalent Fractions- Review What are equivalent fractions? “Equivalent fractions is the name for fractions whose values are the same. ” Strategies we’ve used to find equivalent fractions: • Use a visual fraction model • Multiply the numerator and denominator by the same number • Divide the numerator and denominator by the same number • Look for a relationship between the numerator and denominator • Cross-multiply to check = means “equivalent” and ≠ means “not equivalent”

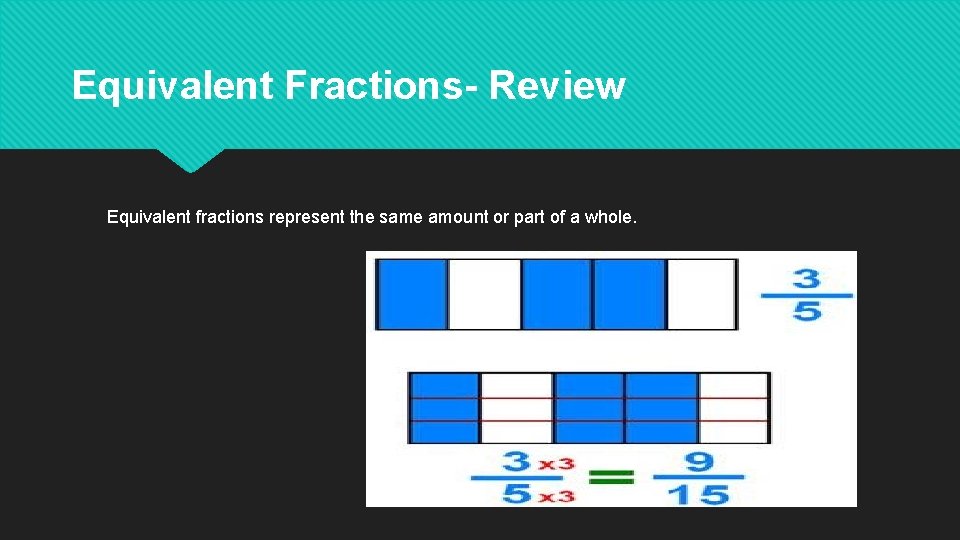
Equivalent Fractions- Review Equivalent fractions represent the same amount or part of a whole.

So what if they’re not equivalent? When we determine that one number (fraction) is greater than or less than another, we are COMPARING. We use these symbols to COMPARE: > means “is greater than” means “is less than” Remember that the opening always faces the larger (greater) amount, but you MUST read the number on the left first!

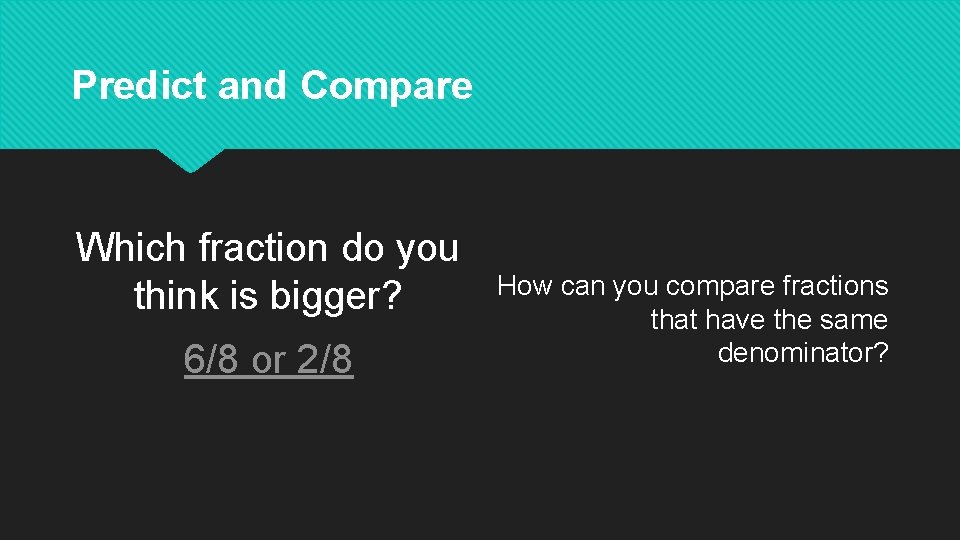
Predict and Compare Which fraction do you think is bigger? 6/8 or 2/8 How can you compare fractions that have the same denominator?

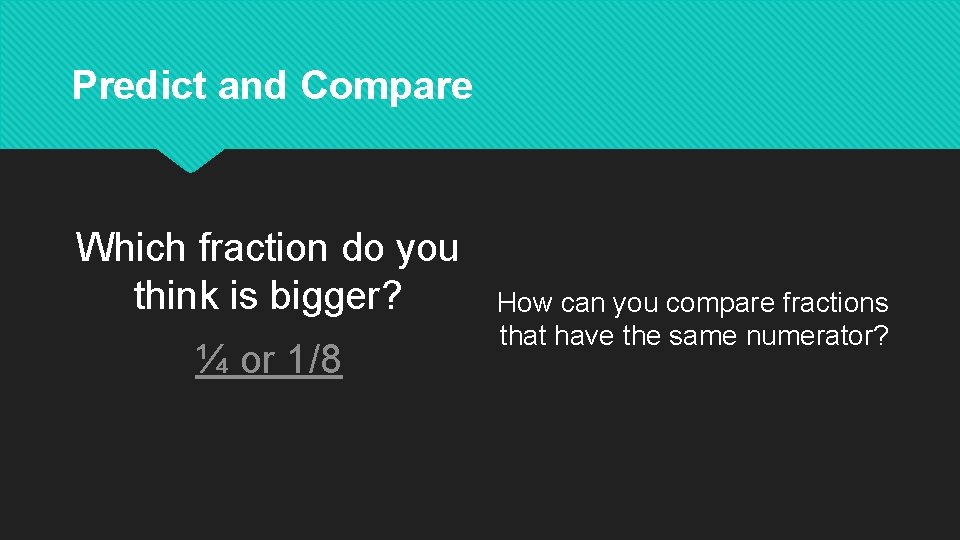
Predict and Compare Which fraction do you think is bigger? ¼ or 1/8 How can you compare fractions that have the same numerator?

Strategies for Comparing Fractions Let’s compare some more fractions by making predictions and testing them using our fractions bars. Brainstorm strategies to compare fractions. Share out.

Strategies for Comparing Fractions Illustrate (make a visual fraction model) and compare. Compare denominators and then numerators Compare to benchmark fractions Find a common denominator to “convert and compare” Cross-multiply to check (also called the “Fishing Pole”)