ITS BETTER TO HAVE A HALFLIFE THAN NO

IT’S BETTER TO HAVE A HALF-LIFE THAN NO LIFE! Radioactive Decay

Radioactivity � An unstable atomic nucleus emits a form of radiation (alpha, beta, or gamma) to become stable. � In other words, the nucleus decays into a different atom. 2

What does it mean to be radioactive? � � Atoms that are radioactive have nuclei that spontaneously decompose to form a different nuclei and produce one or more particles These particles can be any of the following � Alpha particle (42 He) � Beta particle (0 -1 e) � Gamma particle (00γ)

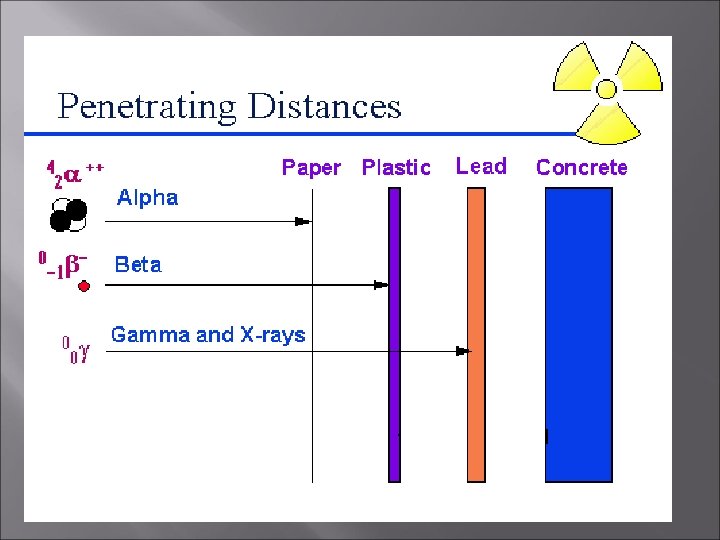
Radioactive (cont’d) � � Atoms that are radioactive have a neutron/proton ratio much greater than 1 Radioactivity can be detected by a Geiger counter

What use is radioactivity? � � Medicine – radioactive materials are used as tracers in the body Energy sources – energy can be obtained through two nuclear processes � Fission: a nucleus divides into smaller fragments � Fusion: nuclei combine to form a larger nucleus

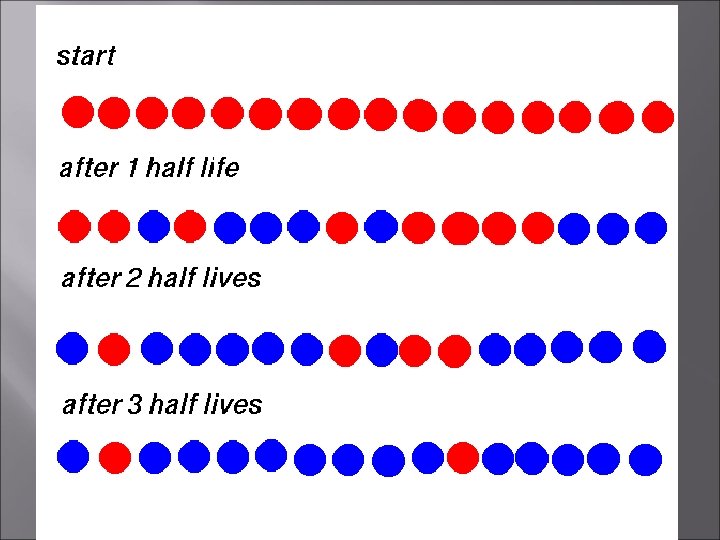
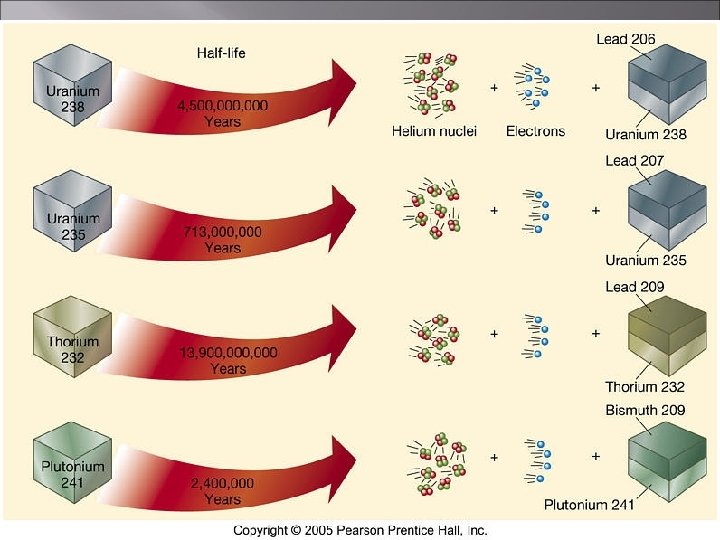
Rate of Decay � The measurement of the time required for a radioactive material to decay is called its half-life. �This is the time required for half of the nuclides in a sample to decay. Half-life of 238 U is 4. 5 billion years Half-life of 131 I is 8. 07 days Half-life of 194 Po is 0. 7 second

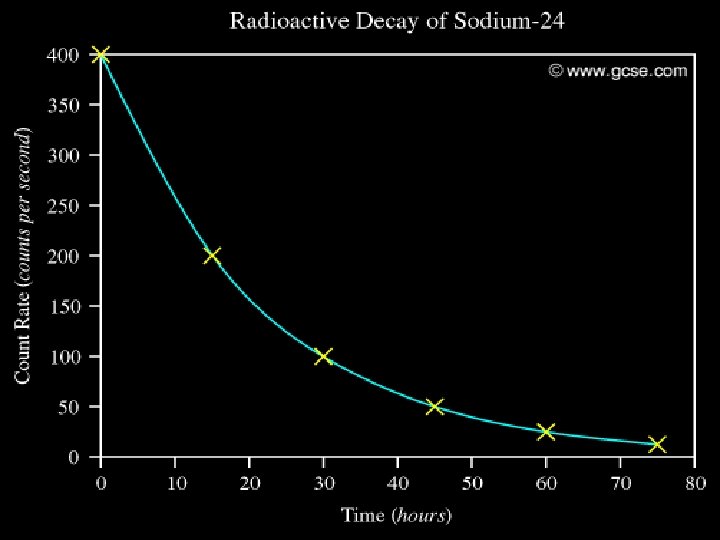
HALF-LIFE

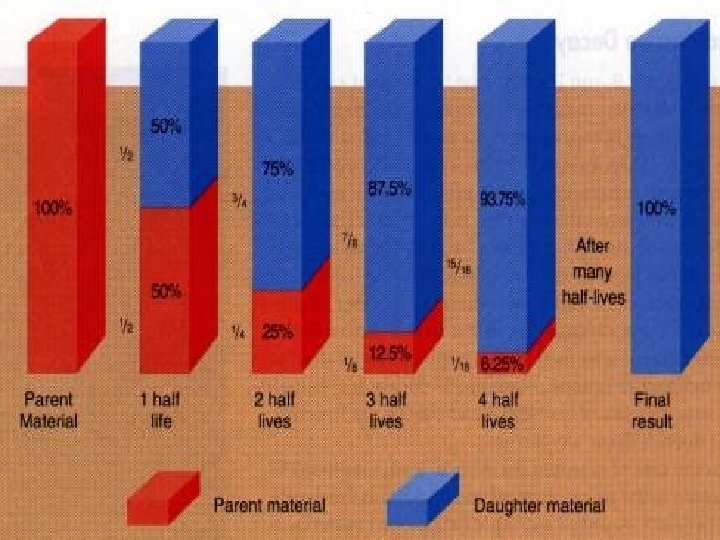
Calculations for half-life � 25 As an example, Technetium-99 has a half-life of 6 hours. This means that, if there is 100 grams of Technetium is present initially, after six hours, only 50 grams of it would be left. After another 6 hours, 25 grams, one quarter of the initial amount will be left. And that goes on like this.

Try it!!! � � Now lets try to solve a half-life calculation problem… Sodium-24 has a half-life of 15 hours. How much sodium-24 will remain in an 18. 0 g sample after 60 hours?

Solution � Initially, Sodium -24 is 18 grams, and after 15 hours, I will have ½ of it left. 60 hours is four half lives The arrows represent the half-life. 18 g 9 g 4. 5 g 2. 25 It goes like this till it reaches ____ grams, in 60 1/2 1/2 hours

Half-Life Calculation #1 � You have 400 mg of a radioisotope with a half-life of 5 minutes. How much will be left after 30 minutes? 14

Half-Life Calculation #2 � Suppose you have a 100 mg sample of Au-191, which has a half-life of 3. 4 hours. How much will remain after 10. 2 hours? 15

Half-Life Calculation # 3 � Cobalt-60 is a radioactive isotope used in cancer treatment. Co-60 has a halflife of 5 years. If a hospital starts with a 1000 mg supply, how many mg will need to be purchased after 10 years to replenish the original supply? 16

Answers to Half-Life Calculations � Half-Life Calculation #1 � 6. 25 mg � Half-Life Calculation #2 � 12. 5 mg � Half-Life Calculation #3 � 750 mg 17

Carbon-14 Dating � � We have some radioactive materials in our bodies. One of the isotopes is carbon-14. Carbon-14 is an isotope of the carbon in CO 2. All living things take it in during respiration.

Carbon-14 Dating � Scientist use carbon-14 to date very old things.

Carbon-14 Dating � � � Decayed carbon-14 is continually being replaced in the body. Once the organism dies the carbon-14 is no longer replaced, but what is there continues to decay. By examining the amount of carbon-14 left in the material, scientist can estimate the age of the subject. The half life of carbon-14 is 5730 years Accurate to about 20, 000 -50, 000 years.

Practice Problems 1) A fossilized tree killed by a volcano was studied. It had 6. 25 percent of the amount of carbon-14 found in a sample of the same size from a tree that is alive today. When did the volcanic eruption take place?

Practice Problems You need to find out how many times ½ (0. 5) must be used as a factor to produce 0. 0625. The answer is 4 times because 0. 5 X 0. 5 = 0. 0625 4 half-lives have gone by and each half-life is 5730 years X 4 = 22, 920 years

Practice Problems 2) A rock was analyzed using potassium-40. The half-life of potassium-40 is 1. 25 billion years. If the rock had only 25 percent of the potassium 40 that would be found in a similar rock formed today, calculate how long ago the rock was formed. Potassium-40 Half-life is 1. 25 billion years

Practice Problems 2) Convert 25% to a decimal --- 0. 25 0. 5 X 0. 5 = 0. 25 2 half-lives have gone by. 1. 25 billion X 2 = 2. 50 billion years

Practice Problems 3) Ash from an early fire pit was found to have 12. 5 percent as much carbon-14 as would be found in a similar sample of ash today. How long ago was the ash formed? Convert 12. 5% to a decimal --- 0. 125 0. 5 X 0. 5 = 0. 125 3 half-lives have gone by. 5730 X 3 = 17, 190 years ago

Practice Problems 4) A rock sample has 12. 5% of the potassium-40 that would be present in a similar rock formed today. How old is the rock sample? Convert 12. 5% to a decimal --0. 5 X 0. 5 = 0. 125 3 half-lives have gone by. 1. 25 billion X 3 = 3. 75 billion years old

Practice Problems 5) How old is a piece of wood in which the carbon 14 is 3. 12% of that in wood formed today? Convert 3. 12% to a decimal --0. 0312 0. 5 X 0. 5 = 0. 03125 5 half-lives have gone by. 5730 X 5 = 28, 650 years old

Half-life equation � Amount remaining = amount of original sample 2 n n = number of half-lives

1) An isotope of cesium (cesium-137) has a halflife of 30 years. If 1. 0 mg of cesium-137 disintegrates over a period of 90 years, how many mg of cesium-137 would remain? Amount remaining = amount 1. 0 of original mg sample 23 n 1 half life = 30 years Therefore, 90 years is equal to how many half lives? n=3

4. Sodium-25 was to be used in an experiment, but it took 3. 0 minutes to get the sodium from the reactor to the laboratory. If 5. 0 mg of sodium-25 was removed from the reactor, how many mg of sodium-25 were placed in the reaction vessel 3. 0 minutes later if the half-life of sodium-25 is 60 seconds? amount of original sample Amount remaining 5. 0 mg = 2 n 3 1 half life = 60 seconds Therefore, 3 minutes is equal to how many half lives? n=3