Turing Machines The Next Level of Computation Turing







































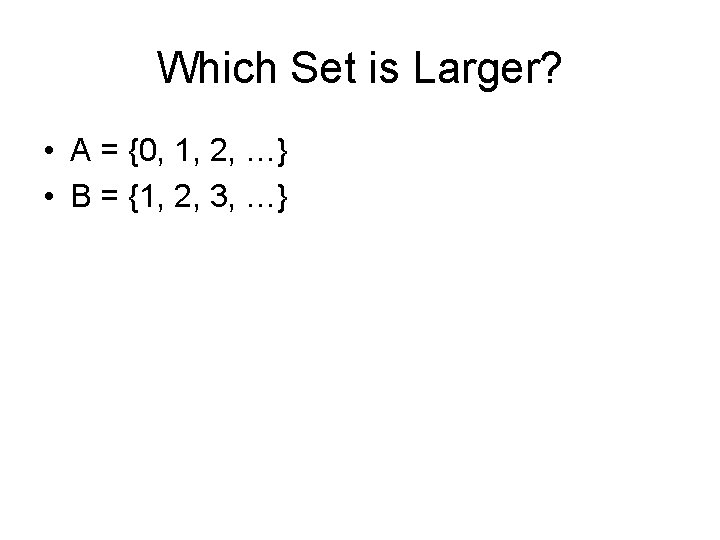














- Slides: 61

Turing Machines

The Next Level of Computation • Turing Machines – From Alan Turing, 1936 • Turns out to be the LAST – The only machine you'll ever need • The Church-Turing Thesis – All algorithms have a Turing Machine equivalent • Some TMs are not algorithms, however

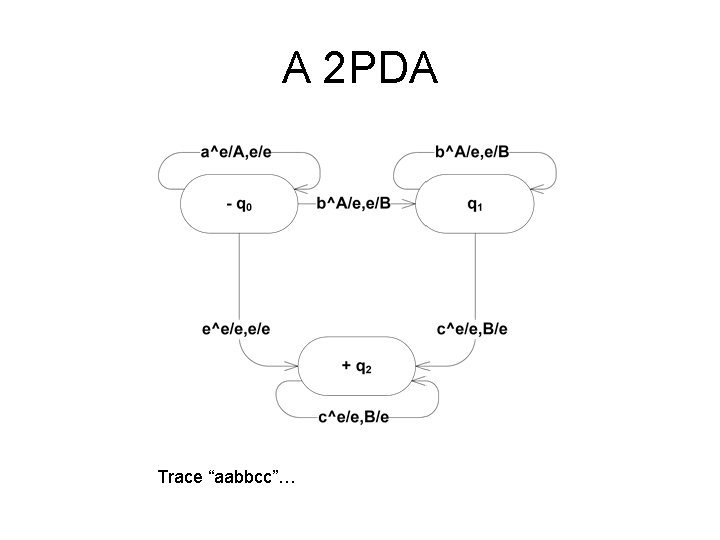
But First… • We have shown that anbncn is not context free – By the Pumping Lemma • What if we add an extra stack to a PDA?

A 2 PDA Trace “aabbcc”…

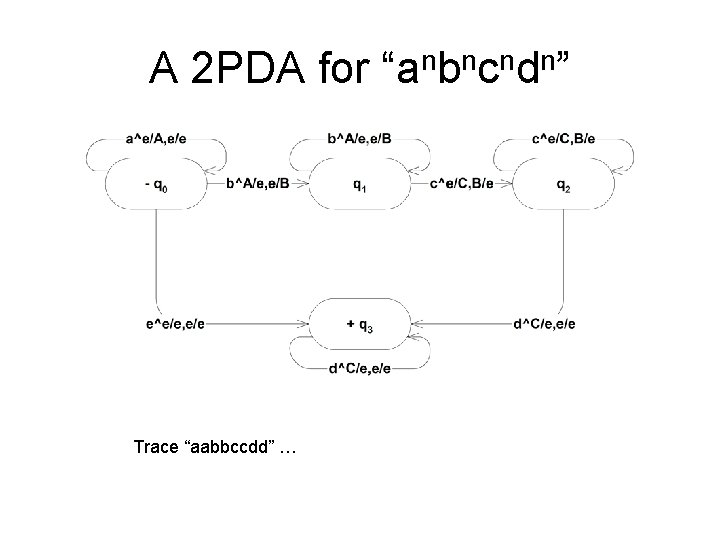
An Observation • • “an” is accepted by an FA “anbn” is accepted by a PDA “anbncn” is accepted by a 2 PDA What about “anbncndn”?

A 2 PDA for “anbncndn” Trace “aabbccdd” …

Interesting Fact • 2 PDA = n. PDA = TM = (many things…)

Perspective • An FA is a machine with no memory • A PDA is like an FA but with unlimited, restricted memory – Restricted because we access it LIFO • A Turing Machine is like an FA but with unlimited, unrestricted memory – We can move to any memory cell • By moving one cell at a time over and over • Can move back and forth – We can both read and write there

Turing Machines Take some states and add… • A one-way-infinite, read/write “tape” – Initialized with input string at left; blanks everywhere else – Machine can replace one character with another – Then it can move to the right or left • Except it can't fall off the left end (“crash”) – Can contain instances of a special “blank” symbol (not part of input alphabet) • A “program” – A set of transitions, plus… – Specifies the character replacements and tape movements

Example • The following TM swaps a's and b's: – q 3 is a “halt state” NOTE: B == “blank”; input is preceded by B here Trace “bab”…

Tracing a TM Execution • Bbab. B Baab. B Baba. B (character about to be read) (halts pointing at 1 st output character)

Turing Machines • A set of states – At least one is a “halting” state – Program halts (and optionally accepts input) • If it crashes, the input is rejected – May leave output on tape • Therefore, can also compute functions • An input alphabet • An output alphabet – Usually contains input alphabet – And a “blank symbol” (not part of input) • A Program

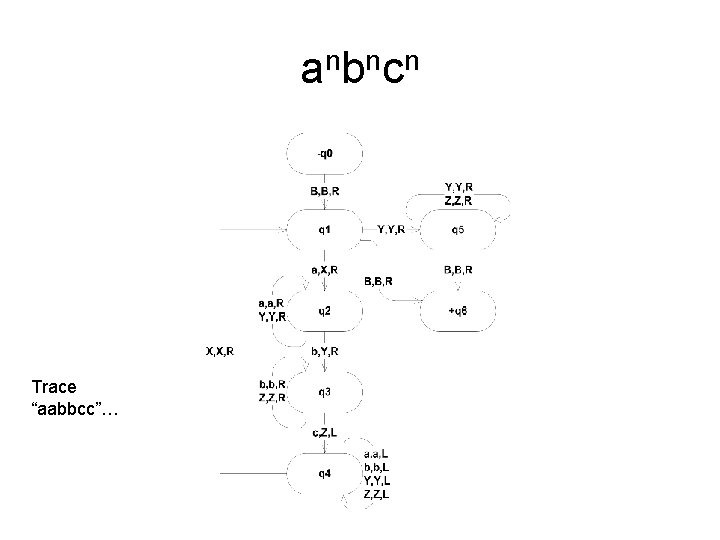
anbncn Trace “aabbcc”…

Tracing “aabbcc” Baabbcc. B BXabbcc. B BXa. Ybcc. B BXa. Yb. Zc. B BXXYb. Zc. B BXXYYZc. B BXXYYZZB BXXYYZZB BXXYYZZBB (halt)

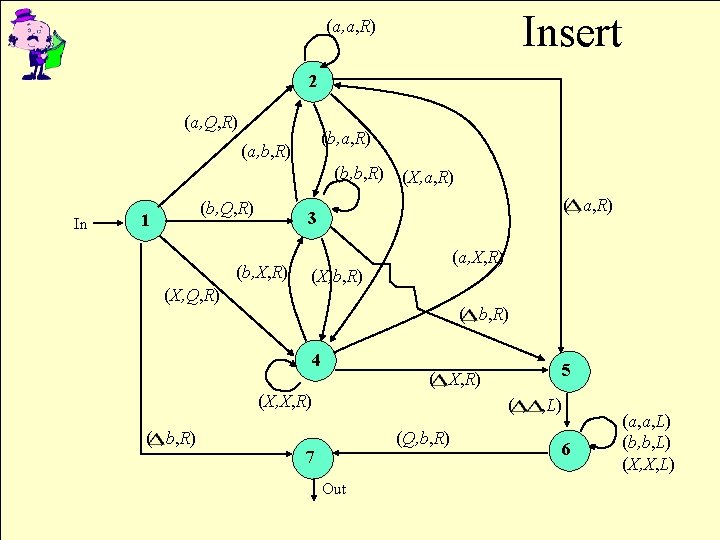
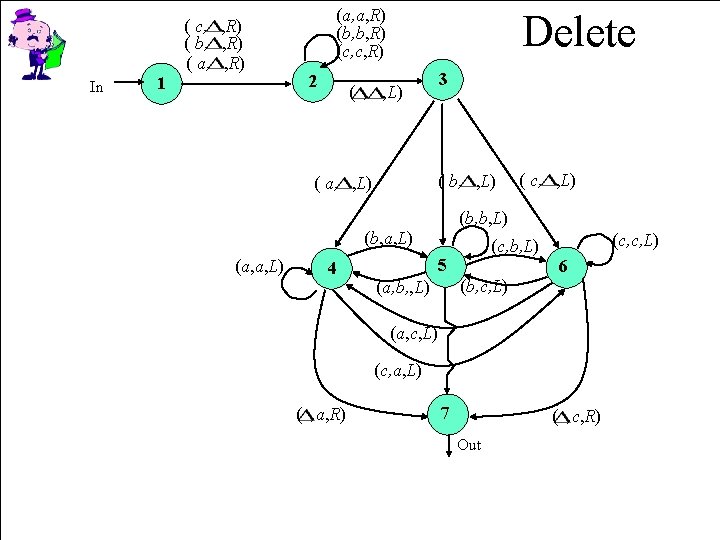
Subroutines • A TM can be used as a subroutine – Just place an arrow from the calling machine to the start state of the subroutine machine • After tape is positioned at the string to be copied – Then every halt state of the subroutine moves back to where you want it to (must copy/paste) • See INSERT on page 451 (next slide) • See DELETE on pp. 452 -453 (second slide) • Can also just chain TMs in a sequence

Insert (a, a, R) 2 (a, Q, R) (b, a, R) (a, b, R) (b, b, R) In (b, Q, R) 1 ( , a, R) 3 (b, X, R) (X, Q, R) (X, a, R) (a, X, R) (X, b, R) ( , b, R) 4 (X, X, R) ( , b, R) 5 ( , X, R) ( , , L) (Q, b, R) 7 Out 6 (a, a, L) (b, b, L) (X, X, L)


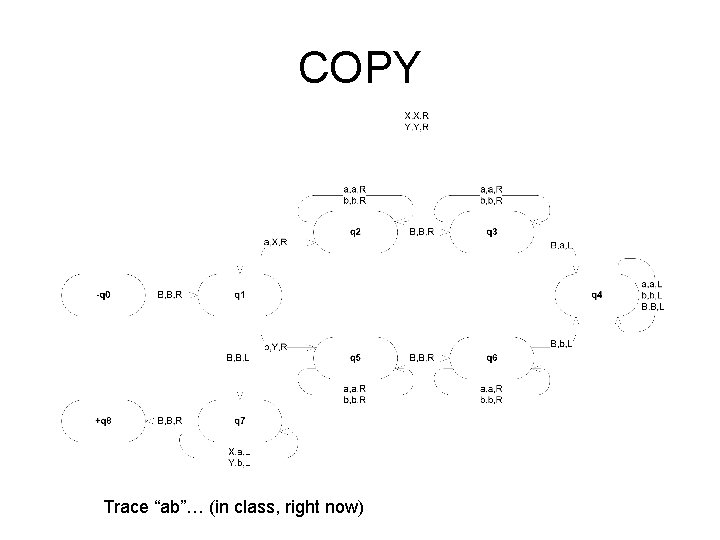
COPY Trace “ab”… (in class, right now)

Copying “ab” Bab. B BXb. BB BXb. Ba BXYBa. B BXYBab BXYBab BXb. Bab Bab (halt)

Mechanisms equivalent to Standard TMs • • PDAs with 2 or more stacks TMs with 2 -way infinite tapes TMs with n tapes or n heads or n-dim tapes TMs with various “move” options – Move by a number of cells (including 0), random cell access by position • • Adding non-determinism to a Standard TM Church's Lambda Calculus (LISP) Unrestricted Phrase Structure Grammars Matrix Grammars Post Systems Markov Algorithms Structured Programming with unlimited memory Any abstract machine yet imagined by man!

Interesting Fact About TMs • They may not halt on every possible input! • And not just because the creator of a specific TM was a doofus • As we shall see, there are languages that are recognizable (if a valid string is input, the TM halts and accepts) – But not decidable (because if an invalid string is input, it will not halt!) • This is the major mathematical/computational discovery of the 20 th century! – There are propositions that cannot be decided (“proven”)

“Algorithms” that may not Halt • Let g(x, y) be some computable function • Let f(x) = the smallest p where g(x, p) = 1, 0, if such a p does not exist • “Pseudo-algorithm” for f(x): m = 0; while (g(x, m) != 1) ++m; cout << m; • If there is no m for a given g and x, then we hang!

A language L over the alphabet is called recursive (aka “Turing computable” or “Turing decidable”) if there is a TM T that accepts every word in L and rejects every word in L'; that is, accept(T) = L reject(T) = L' A TM that recognizes a recursive set is a model of an algorithm. It always halts.

Halting • It is possible that TMs will not halt for certain inputs – Infinite loop • Due to the nature of the language or computation • This is the price we pay for such a flexible computation model as TMs • 3 possibilities when a TM processes an input string from a non-recursive language: – Accepts (goes to a halt state) – Rejects (crashes) – Hangs (infinite loop)

A language L over the alphabet is called recursively enumerable (aka “Turing recognizable”) if there is a TM T that accepts every word in L and either rejects (crashes) or loops forever for every word in the language L', the complement of L: accept(T) = L reject(T) + loop(T) = L' Recursive sets are r. e, of course. Just like regular languages are vacuously context-free.

Important Facts • There exist languages that are r. e. but not recursive – You'll see one shortly • There exist languages that aren't even r. e. ! – (Again, you'll see one soon) • All are “contrived” – They don't arrive in “practice” • They just make mathematicians feel smart : -) – Languages generated by grammars are r. e. or “better”

Closure Properties • All r. e. languages are closed under union, intersection, concatenation, and Kleene* – Everything but complement! • Recursive languages are also closed under complement • Also: If L and L' are r. e. , then L is recursive • Here come the Proofs…

Complements of Recursive Languages • Let M be a machine that decides a recursive language, L • Form the machine M' by inverting the acceptability of M – Goes to a reject state instead • Then M' decides L' – So L' is recursive

Complements of r. e. Languages • Suppose L and L' are both r. e. • Let M recognize L, and M' recognize L' – M may hang on elements of L', but M' doesn't • Form a new machine, M* that calls M and M' in parallel (non-deterministically) – If M accepts w, so does M* – If M' accepts w, reject w – There are no other possibilities! (No hanging) – Therefore, L is recursive, by definition

Pit Stop/Review • TMs can recognize strings from certain languages and/or compute functions • If there is a TM, M, that accepts a language, L, and M always halts, then L is recursive – Also called decidable – M constitutes an algorithm for L • If there is no such M for a language, L 1, but there is instead a machine M 1 that accepts every string in L 1, but M 1 may hang on strings not in L 1, then L 1 is recursively enumerable

Pit Stop (continued) • The complement of a recursive language is recursive – Recursive languages are closed under all operations, like regular languages are • r. e. languages are closed under intersection • The complement of a r. e. language may not be r. e. – If it is, then both languages are recursive!

Universal Turing Machines • TMs that process partitioned input: – A “code” section and a “data” section • A UTM simulates the actions of the input TM (the “code”) on the input data • Requires encoding TM instructions as data – Using separator characters

A Sample TM Encoding • • a=1 b = 11 B = 111 q 0 = 1 q 1 = 11 qn = 1(n+1) L=1 R = 11 • Use 000 to delimit machine components • Use 00 to delimit transitions • A TM is just a big binary string! (So they're enumerable!) • The UTM reads a character, searches for the transition that applies, updates the state and tape

The Totality of TMs is Enumerable • In other words, they are countable – They can be arranged in a sequence • TM 1, TM 2, etc. • Why? – Because they can be encoded as strings fed unto a Universal TM – Strings can be ordered lexicographically – So there you have it!

Interlude • The Halting Dog Problem

The Halting Problem • Question: Is there a TM (H) that takes another TM (M) as input, along with an input string (w), and decides whether or not M halts on w? – In other words, is there such an algorithm? • This would be very useful – Could detect infinite loops in bad code! – Or could save us from wasting precious time

The Halting Problem • Suppose there is such a machine, H – This is the dog, Meg, before retraining • Since all TMs are enumerable, we could apply H to all such TMs • Construct a table of the outputs of applying H to all TMs • If the machine won't halt, insert 0 or some other special value

The Halting Problem • The halt detector is depicted below:

The Halting Problem (cont. ) • Question: What happens when we replace M and w with H and its encoding, resp. ? So far so good…

The Halting Problem (cont. ) (“Retraining Meg”) • Now, define a machine D as follows… That is, D(x) calls H(x, x) and inverts the result. Question: What is the result of D(D)?

Contradiction • D accepts D iff D doesn’t halt on D • Huh?

The Halting Problem (cont. ) • Conclusion: there can be no such machine, H • The Halting Problem is undecidable • Many problems are shown to be unsolvable by showing them to be logically equivalent to the Halting Problem – i. e. , show that H => P • There are unsolvable problems • Just like there are unprovable propositions – Godel's Incompleteness Theorem

A Non-recursive Language • Let P be the set of all pairs (M, w) such that the machine M halts on input w • This is r. e. because we can just input M and w into a UTM, U – U will either halt (accept), crash (reject), or hang (this is the very definition of r. e. ) – In fact, U will halt on each element of P • By definition! • But we just showed that it is not recursive – Because the Halting Problem is undecidable

A non-r. e. Language! • Consider P': – P' = {Set of all (M, w) where either M is not a TM encoding, or M does not halt on w} • If P' were r. e. , then P and P' would both be recursive – Since we proved that if a language and its complement are r. e. , they are both recursive! • So P‘ is not r. e. !

Yet Another Look • There are more languages than there are Turing Machines – this will prove the existence of non r. e. languages • How can you prove this? – By showing that the number of languages is uncountable (not “enumerable”)
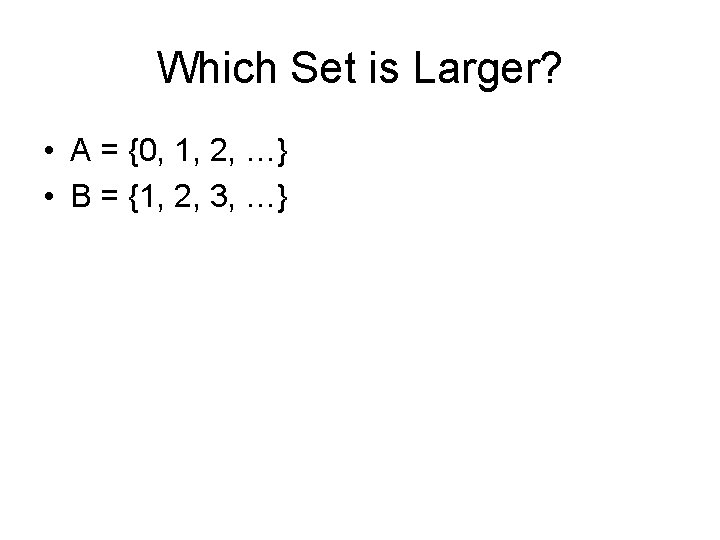
Which Set is Larger? • A = {0, 1, 2, …} • B = {1, 2, 3, …}

A 1 -to-1 Correspondence • The function f: A => B defined as f(n) = n+1 is a 1 -to-1 correspondence between A and B • Therefore, their cardinality is the same – Welcome to infinity!

How “Big” is a Language? • A Language is a subset of Σ* • We can write the elements of Σ* in lexicographical order • Therefore, there is a first one, a second one, etc. – So, the strings of a language are enumerable – Every language is a countable set of strings

How Many Real Numbers are There? • The real numbers are uncountable – They cannot be mapped in a 1 -to-1 fashion to the counting numbers • Proof: – Assume they can be – Arrange their digits in a table a[ ][ ] – The sequence a[n][n]+1 is not in the table!

How Many Bit Strings are There? • This also has to be uncountable – Real numbers can be seen as bit strings • But if you need convincing, use diagonalization again: – Arrange the supposedly countable number of bits strings in a table – The bit string where you flip the diagonal bits is not in the table!

How Many Languages Are There? • It is an uncountable number! • Associate an infinite bit string with each subset of Σ* – Bit-n is 1 if string sn is in some language L • Each bit string represents a language! – But the number of such bit strings is uncountable • Therefore, there an uncountable number of languages over Σ*

There are More Languages than TMs! • Follows from the previous slide – Another way to say it: – There is no 1 -to-1 mapping from N => 2 N • TMs are countable, the # of languages is not • Therefore, some languages cannot be recognized by a TM – There aren't enough TMs to go around – Just like there are more reals than integers • So, non-r. e. languages must exist! – “More” than are r. e. !

Undecidable Problems • Does a TM halt on all input? • Does an unrestricted grammar generate any strings? • Is the language of a TM finite? • Many more…

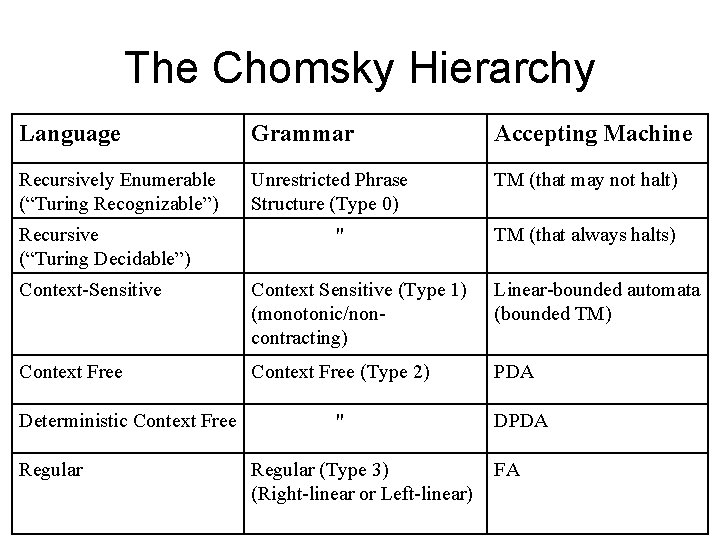
The Chomsky Hierarchy Language Grammar Accepting Machine Recursively Enumerable (“Turing Recognizable”) Unrestricted Phrase Structure (Type 0) TM (that may not halt) Recursive (“Turing Decidable”) " TM (that always halts) Context-Sensitive Context Sensitive (Type 1) (monotonic/noncontracting) Linear-bounded automata (bounded TM) Context Free (Type 2) PDA Deterministic Context Free Regular " Regular (Type 3) (Right-linear or Left-linear) DPDA FA

Unrestricted Phrase Structure Grammars • Left-hand side of the rule can have multiple symbols – Must have at least one non-terminal, though • Introduces context-sensitive replacement • “Type 0” Grammar

A Grammar for anbncn S → a. Abc | abc | e Ab → b. A Ac → Bbcc b. B → Bb a. B → aa | aa. A S a. Abc ab. Ac ab. Bbcc a. Bbbcc aabbcc An A is created as the left-most variable. It travels to the right until it finds a 'c', then creates a new b and c, and becomes a B. The B moves back to create the extra needed a. The last rule allows the option to do it all over again (by introducing another A). This is similar to what the Turing machine for the same language does, except the TM recognizes instead of generates the letters.

About Unrestricted Grammars • Cannot use the decidability algorithms for CFGs – CYK algorithm does not apply • No “Normal Form” • Non-null productions may create shorter strings • Terminals can disappear!

Context-Sensitive Grammars • Like Unrestricted Grammars except: – Right-hand side must be no shorter than left-hand side • So strings never shrink – Hence the name “non-contracting” or “monotonic” – Cannot contain lambda (the empty string) • Context-sensitive languages don't need unlimited memory – Since intermediate sentential forms never contract, the largest memory requirement is |w| – Accepting machine: Linear Bounded Automaton • A TM with limited memory

anbncn, n>0 is Context Sensitive S → a. Abc | abc Ab → b. A Ac → Bbcc b. B → Bb a. B → aa | aa. A

Matrix Grammars • Like Phrase Structure • S S 1 S 2 a. S 1 b. S 2 c Grammars, but sets of aa. S 1 bb. S 2 cc rules must be applied aabbcc in sequence • P 1: S → S 1 S 2 P 2: S 1 → a. S 1, S 2 → b. S 2 c P 3: S 1 → e, S 2 → e • Generates anbncn

Church-Turing Thesis • "It is believed that there are no functions that can be defined by humans, whose calculation can be described by any welldefined mathematical algorithm that people can be taught to perform, that cannot be computed by TMs. The TM is believed to be the ultimate calculating mechanism. "
 X.next = x.next.next
X.next = x.next.next Alan turing julius mathison turing
Alan turing julius mathison turing Turing machine 7 tuple
Turing machine 7 tuple Next level innovations
Next level innovations Next level content
Next level content Next level building
Next level building Wtax compensation table
Wtax compensation table Expanded withholding tax computation
Expanded withholding tax computation Expanded withholding tax computation
Expanded withholding tax computation Form 2306
Form 2306 Fertilizer computation examples
Fertilizer computation examples Eecs 1019
Eecs 1019 Sipser, m: introduction to the theory of computation
Sipser, m: introduction to the theory of computation Nolco and mcit illustration
Nolco and mcit illustration Income tax computation format
Income tax computation format Crystalloids and colloids examples
Crystalloids and colloids examples Individual tax computation format
Individual tax computation format Data cube computation methods
Data cube computation methods Drug calculation formula
Drug calculation formula Data cube computation
Data cube computation Data cube computation
Data cube computation Infusion flow rate formula
Infusion flow rate formula Cuts of a distributed computation
Cuts of a distributed computation Theory of computation
Theory of computation Withholding tax form 2307
Withholding tax form 2307 Computation of wealth tax
Computation of wealth tax Board feet computation
Board feet computation What is transition graph
What is transition graph Types of languages in theory of computation
Types of languages in theory of computation The pagerank citation ranking bringing order to the web
The pagerank citation ranking bringing order to the web Pagerank computation
Pagerank computation The pagerank citation ranking: bringing order to the web
The pagerank citation ranking: bringing order to the web Binary search in secure computation
Binary search in secure computation Computation symbols
Computation symbols Computation of machine hour rate
Computation of machine hour rate Media computation
Media computation Theory of computation
Theory of computation Types of error in numerical methods
Types of error in numerical methods Pagerank computation
Pagerank computation Computation examples
Computation examples Computation
Computation Theory of computation
Theory of computation The purpose of computation is insight not numbers
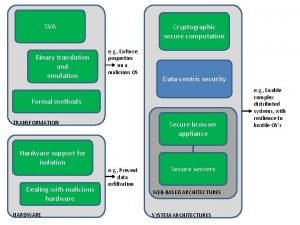
The purpose of computation is insight not numbers Privacy-enhancing computation
Privacy-enhancing computation Ram model of computation
Ram model of computation Theory of computation
Theory of computation Dqage
Dqage Theory of computation
Theory of computation Cosc 3340
Cosc 3340 Time hierarchy theorem proof
Time hierarchy theorem proof Common lisp a gentle introduction to symbolic computation
Common lisp a gentle introduction to symbolic computation Ucl bsc computer science
Ucl bsc computer science Anbncn pda
Anbncn pda Theory of computation quiz
Theory of computation quiz Multiparty computation
Multiparty computation Two round multiparty computation via multi-key fhe
Two round multiparty computation via multi-key fhe Nfa theory of computation
Nfa theory of computation Computation structure
Computation structure Self adjusting computation
Self adjusting computation Secure multiparty computation
Secure multiparty computation Computation history
Computation history Nutrition29
Nutrition29