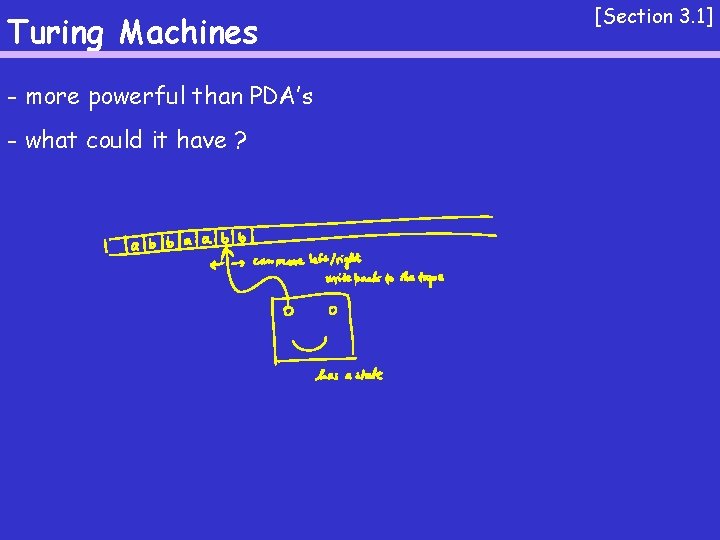
Turing Machines more powerful than PDAs what could

Turing Machines - more powerful than PDA’s - what could it have ? [Section 3. 1]

Turing Machines Example: A = { aibici | i ¸ 0 } [Section 3. 1]

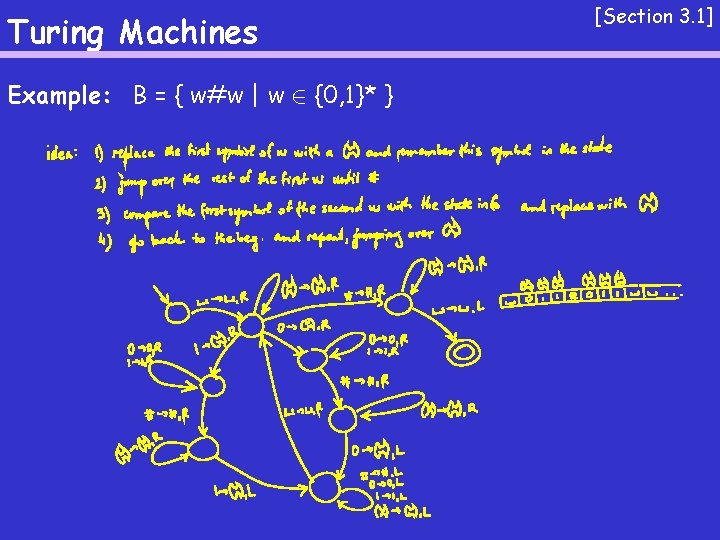
Turing Machines Example: B = { w#w | w 2 {0, 1}* } [Section 3. 1]

[Section 3. 1] Turing Machines Def 3. 3: A Turing machine (TM) is a 7 -tuple (Q, §, ¡, ±, q 0, qaccept, qreject), where - Q is the (finite) set of states - § is the (finite) input alphabet, not containing □ - ¡ is the (finite) tape alphabet, □[§ µ ¡ - ±: is the transition function - q 0 2 Q - qaccept 2 Q is the accept state - qreject 2 Q-{qaccept} is the reject state

Turing Machines [Section 3. 1] Computation of Turing machines - first we define a configuration : uqv – means the tape contains uv, the state is q, and the machine reads the first symbol of v - suppose configuration is uaqbv and ±(q, b)=(p, c, R) We say that uaqbv yields

Turing Machines [Section 3. 1] Computation of Turing machines - first we define a configuration : uqv – means the tape contains uv, the state is q, and the machine reads the first symbol of v - start configuration : - accepting configuration : - rejecting configuration : Note: accepting/rejecting configurations are halting

Turing Machines [Section 3. 1] Computation of Turing machines - first we define a configuration : uqv – means the tape contains uv, the state is q, and the machine reads the first symbol of v A TM M accepts w if The language of a TM Mis the set of strings that M accepts/recognizes.

Turing Machines [Section 3. 1] Def 3. 5: A language is Turing-recognizable if there is some TM that recognizes it. Def 3. 6: A language is Turing-decidable if there is some TM that decides it.

Turing Machines Example: A = { 0 n | n=2 k for some k ¸ 0 } [Section 3. 1]