Turing Machines Chapter 3 1 1 Plan Turing

Turing Machines Chapter 3. 1 1

Plan • Turing Machines(TMs) – Alan Turing • Church-Turing Thesis – Definitions • Computation • Configuration • Recognizable vs. Decidable – Examples – Simulator 2

Alan Turing was one of the founding fathers of CS. • His computer model the Turing Machine(1936) was the inspiration for the electronic computer that came two decades later • Was instrumental in cracking the Nazi Enigma cryptosystem in WWII • Invented the “Turing Test” used in AI • The Turing Award. Pre-eminent award in Theoretical CS (called the “Nobel Prize” of CS) 3

Church-Turing Thesis • Thesis- Every effectively calculable function is a computable function • Everything that is computable by a Turing machine • The thesis remains a hypothesis – Despite the fact that it cannot be formally proven the Church–Turing thesis now has near-universal acceptance. 4

Turing Machine • Most powerful machine so far… – Similar to a finite automata 1. 2. 3. 4. Uses infinite tape as memory Can both read from and write to the tape Read/write head can move left/right Accept/reject take affect immediately • Cannot solve all problems

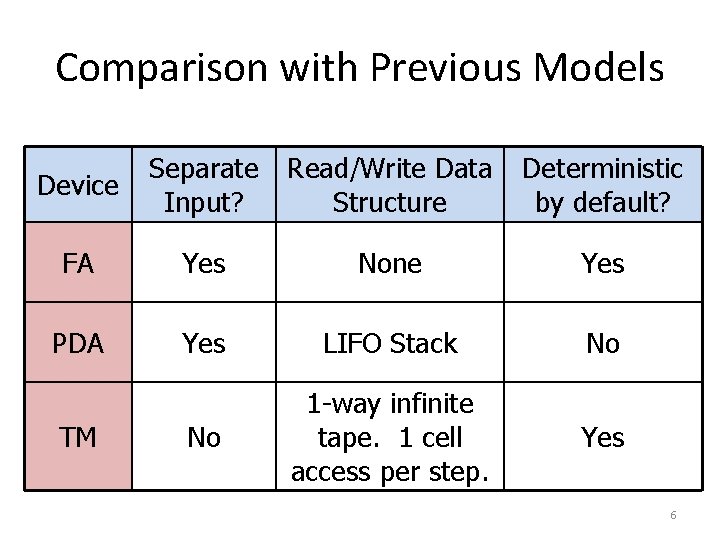
Comparison with Previous Models Device Separate Read/Write Data Deterministic Input? Structure by default? FA Yes None Yes PDA Yes LIFO Stack No No 1 -way infinite tape. 1 cell access per step. Yes TM 6

Formal Definition of a TM 7

Successor Program • Sample Rules: 1. If read 1, write 0, go right, repeat. 2. If read 0, write 1, HALT! 3. If read “”, write 1, HALT! • Using these rules on a tape containing the reverse binary representation of 47 we obtain: 8

Successor Program If read 1, write 0, go right, repeat. If read 0, write 1, HALT! If read � “”, write 1, HALT! 1 1 0 1 9

Successor Program If read 1, write 0, go right, repeat. If read 0, write 1, HALT! If read � “”, write 1, HALT! 0 1 1 1 0 1 10

Successor Program If read 1, write 0, go right, repeat. If read 0, write 1, HALT! If read “”, write 1, HALT! 0 0 1 11

Successor Program If read 1, write 0, go right, repeat. If read 0, write 1, HALT! If read � “”, write 1, HALT! 0 0 0 1 12

Successor Program If read 1, write 0, go right, repeat. If read 0, write 1, HALT! If read � “”, write 1, HALT! 0 0 0 1 13

Successor Program If read 1, write 0, go right, repeat. If read 0, write 1, HALT! If read “”, write 1, HALT! 0 0 1 1 14

Successor Program So the successor’s output on 111101 was 000011 which is the reverse binary representation of 48. Similarly, the successor of 127 should be 128: 15

Successor Program If read 1, write 0, go right, repeat. If read 0, write 1, HALT! If read “”, � write 1, HALT! 1 1 1 16

Successor Program If read 1, write 0, go right, repeat. If read 0, write 1, HALT! If read � “”, write 1, HALT! 0 1 1 1 17

Successor Program If read 1, write 0, go right, repeat. If read 0, write 1, HALT! If read “”, write 1, HALT! 0 0 1 1 18

Successor Program If read 1, write 0, go right, repeat. If read 0, write 1, HALT! If read � “”, write 1, HALT! 0 0 0 1 1 19

Successor Program If read 1, write 0, go right, repeat. If read 0, write 1, HALT! If read � “”, write 1, HALT! 0 0 1 1 1 20

Successor Program If read 1, write 0, go right, repeat. If read 0, write 1, HALT! If read � “”, write 1, HALT! 0 0 0 1 1 21

Successor Program If read 1, write 0, go right, repeat. If read 0, write 1, HALT! If read � “”, write 1, HALT! 0 0 0 1 22

Successor Program If read 1, write 0, go right, repeat. If read 0, write 1, HALT! If read � “”, write 1, HALT! 0 0 0 0 23

Successor Program If read 1, write 0, go right, repeat. If read 0, write 1, HALT! If read � “”, write 1, HALT! 0 0 0 0 1 24

Drawing the machine • Draw the machine – Description 1. 2. 3. If read 1, write 0, go right, repeat. If read 0, write 1, HALT! If read � “”, write 1, HALT! 25

TM Dynamic Picture • A string w is accepted by M if after being put on the tape then letting M run, M eventually enters the accept state. Therefore, w is an element of L(M) - the language accepted by M. • We can formalize this notion as follows: 26

TM Formal Definition Dynamic Picture Suppose TM’s configuration at time t is given by uapxv where p is the current state, ua is what’s to the left of the head, x is what’s being read, and v is what’s to the right of the head. If d(p, x) = (q, y, R) then write: uapxv uayqv With resulting configuration uaypv at time t+1. If, d(p, x) = (q, y, L) instead, then write: uapxv uqayv There also two special cases: – head is forging new ground –pad with the blank symbol � – head is stuck at left end –by def. head stays put NOTE: “ ” is read as “yields” 27

TM outcomes Three possibilities occur on a given input w : 1. The TM M eventually enters qacc and therefore halts and accepts. (w L(M) ) 2. The TM M eventually enters qrej or crashes somewhere. M rejects w. (w L(M) ) 3. Neither occurs! I. e. , M never halts its computation and is caught up in an infinite loop, never reaching qacc or qrej. In this case w is neither accepted nor rejected. However, any string not explicitly accepted is considered to be outside the accepted language. (w L(M) ) 28

Recognizable vs. Decidable • Recognizable- The TM recognizes the language but doesn’t necessarily reach an accept or reject state (could loop FOREVER ) • Decidable- is recognizable and guaranteed to reach an accept or reject state (without the possibility for an infinite loop ) 29

Bit-shifting example 30

31

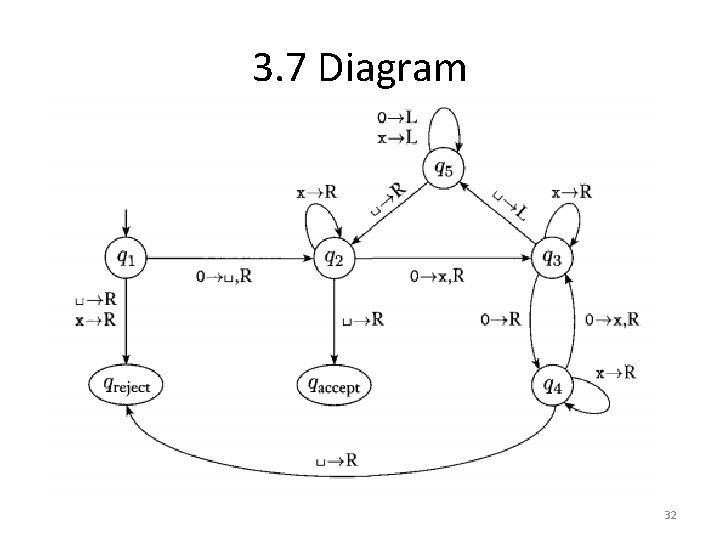
3. 7 Diagram 32

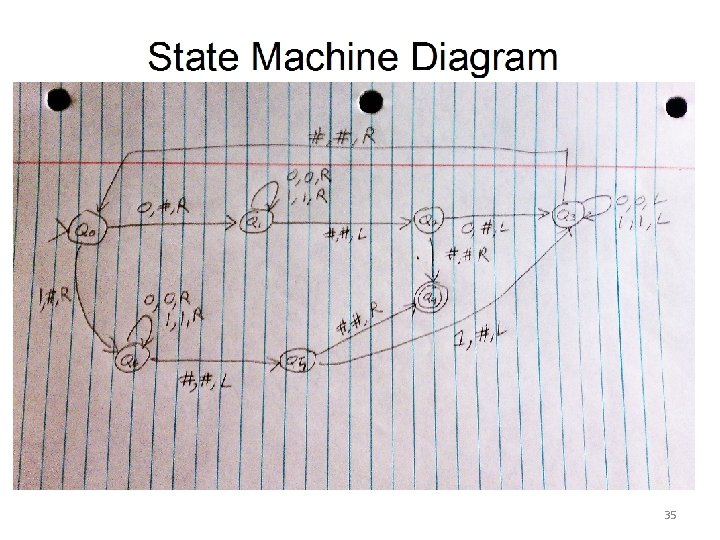
Fall 2010 Exam 2 Question 1 1) (25 pts) Give the full, formal description of a Turing Machine that accepts the following language: L = { w#w. R | where w consists of only 0 s and 1 s and has length at least 1. } The input alphabet will be {0, 1, #}. The tape alphabet will include 0, 1, #, B, and any other symbols you choose to include in it. Give a simple intuitive description of what each state in the machine represents. And draw the diagram for this machine. 33

34

35

36

Simulator • Accepts 4 or 5 tuples – (Start, input, New. State, output, Direction) – (Start, input, New. State, Di rection OR output) • One tape • http: //ironphoenix. org/ tril/tm/ 37

END 38