MQUINAS DE TURING Teora del Autmata Definicin Definimos

MÁQUINAS DE TURING Teoría del Autómata

Definición Definimos una máquina de Turing como una 7 -tupla M = (Q, S, G, s, b, F, d), donde Q es un conjunto finito de estados S es un alfabeto de entrada G es un alfabeto llamado alfabeto de la cinta s Q es el estado inicial b G es el símbolo blanco F Q es el conjunto de estados finales o de aceptación d: Q G {L, R} es una función parcial que se llama función de transición

La cinta La máquina de Turing posee una cinta dividida en celdas, cada celda es capaz de almacenar un símbolo. Además posee una cabeza lectora/escritora que lee y escribe un símbolo en la cinta. Inicialmente la cinta contiene b en todas sus celdas. La función de transición d transforma pares (q, s) en ternas de la forma (p, t, X), donde p es el siguiente estado, t es el símbolo escrito en la cinta y X es el movimiento de la cabeza lectora/escritora, que puede ser L o R. a d(q 1, a) = (q 5, b, R) b b Posición de la cabeza lectora/escritora Estado interno q 1 b b b Posición de la cabeza lectora/escritora Estado interno q 5

Representación instantánea Se puede dar una descripción instantánea de la máquina de Turing similar a la de los ADPND, para la transición anterior sería (q 1, abb) ├─ (q 5, bbb) el carácter subrayado indica la posición de la cabeza lectora/escritora. Otra posibilidad es anteponer el estado actual al carácter señalado por la cabeza lectora/escritora como se muestra q 1 abb ├─ bq 5 bb

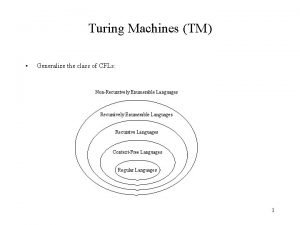
Máquinas de Turing como aceptadores de lenguajes Sea M = (Q, S, G, s, b, F, d) una máquina de Turing. Entonces el lenguaje aceptado por M es L(M) = {w S* | q 1 w ├─* w 1 pw 2 para p F y wi G*} Los lenguajes aceptados por las máquinas de Turing se conocen como lenguajes recursivamente enumerables. Una cadena puede rechazarse por una máquina de Turing si se termina de procesarla en un estado de no aceptación. Otra forma es rechazarla al entrar en un bucle infinito.

Ejemplo El lenguaje regular a* es aceptado por la máquina Q = {q 1, q 2}, s = q 1, F = {q 2}, d(q 1, a) = (q 1, a, R) y d(q 1, #) = (q 2, #, R) También puede se aceptar por la máquina: Q = {q 1, q 2 , q 3}, s = q 1, F = {q 3}, d(q 1, a) = (q 1, a, R) d(q 2, a) = (q 2, a, R) d(q 1, b) = (q 2, b, R) d(q 2, b) = (q 2, b, R) d(q 1, #) = (q 3, #, R) d(q 2, #) = (q 2, #, R)

Ejemplo El lenguaje anbn es aceptado por la máquina Q = {q 1, q 2 , q 3 , q 4}, s = q 1, F = {q 5} d(q 1, a) = (q 2, c, R) d(q 2, d) = (q 2, d, R) d(q 2, a) = (q 2, a, R) d(q 2, b) = (q 3, d, L) d(q 3, d) = (q 3, d, L) d(q 3, a) = (q 3, a, L) d(q 3, c) = (q 1, c, R) d(q 1, d) = (q 4, d, R) d(q 4, #) = (q 5, #, L) d(q 4, d) = (q 4, d, R)

Ejemplo El siguiente grafo muestra una máquina de Turing transforma una cadena de la forma anbam en an+mb mediante la siguiente función de transición: d(q 1, a) = (q 1, a, R) d(q 1, b) = (q 2, a, R) d(q 2, a) = (q 2, a, R) d(q 2, #) = (q 3, #, L) d(q 3, a) = (q 4, b, L) d(q 4, a) = (q 4, a, L) d(q 4, #) = (q 5, #, R)

Maquinas de Turing y lenguajes Una máquina de Turing que acepta un lenguaje no necesita detenerse para cualquier cadena de entrada, solo para las que pertenecen al lenguaje. Hay lenguajes RE para los cuales ninguna máquina de Turing que los acepte para con todas las entradas. La subclase de lenguajes que son aceptados al menos por una máquina de Turing que para con toda cadena de entrada se llaman lenguajes recursivos.

Funciones Turing computables Se dice que una función de cadena f e s. Turing computable si existe una máquina de Turing M = (Q, S, G, q 1, #, F, d) para la cual q 1 w |–* qf u para algún qf F, cuando f (w) = u. La función f (m, n) = m + n se puede implementar con d(q 1, a) = (q 1, a, R) d(q 3, a) = (q 4, b, L) d(q 1, b) = (q 2, a, R) d(q 4, a) = (q 4, a, L) d(q 2, a) = (q 2, a, R) d(q 4, #) = (q 5, #, R) d(q 2, c) = (q 3, b, L)

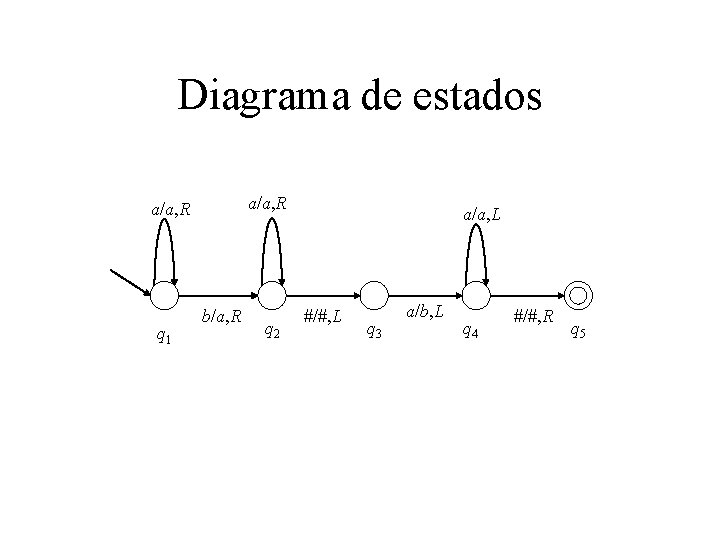
Diagrama de estados a/a, R q 1 b/a, R q 2 a/a, L #/#, L q 3 a/b, L q 4 #/#, R q 5

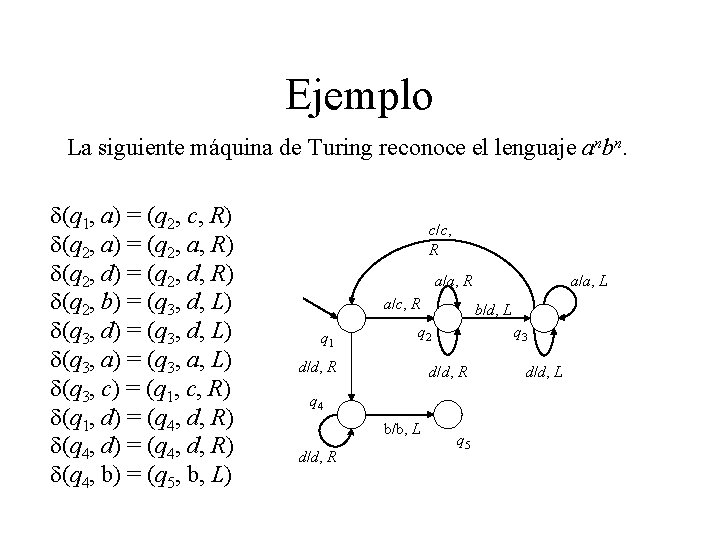
Ejemplo La siguiente máquina de Turing reconoce el lenguaje anbn. d(q 1, a) = (q 2, c, R) d(q 2, a) = (q 2, a, R) d(q 2, d) = (q 2, d, R) d(q 2, b) = (q 3, d, L) d(q 3, d) = (q 3, d, L) d(q 3, a) = (q 3, a, L) d(q 3, c) = (q 1, c, R) d(q 1, d) = (q 4, d, R) d(q 4, b) = (q 5, b, L) c/c, R a/a, R a/c, R q 1 b/d, L q 2 d/d, R q 3 d/d, R q 4 b/b, L d/d, R a/a, L q 5 d/d, L

Construcción de Máquinas de Turing Definición. Sean M 1 y M 2 dos máquinas de Turing sobre el mismo alfabeto de entrada S y el mismo alfabeto de salida G, donde M 1 = (Q, S, G, s 1, b, F 1, d 1) M 2 = (Q, S, G, s 2, b, F 2, d 2) se supone Q 1 Q 2 = , La composición de máquinas de Turing M 1 y M 2 es la máquina de Turing M = (Q, S, G, s, b, F, d), que se denota por M 1 M 2. donde Q = Q 1 Q 2 s=s 1 F = F 2 d= { d 1(q, s) si q Q 1 y d 1(q, s) (p, t, X) p F 1 d 2(q, s) si q Q 2 (s 2, t, X) si q Q 1 y d 1(q, s) =(p, t, X) para algún p F 1

Bloques de construcción Definimos Rb como la máquina M 1 con F 1 = {q 4} con Definimos M 1 M 2 estará dada por d 1(q 1, a) = (q 2, a, R) d 1(q 1, #) = (q 2, #, R) d 1(q 2, a) = (q 2, a, R) d 1(q 2, #) = (q 3, #, L) d 1(q 3, #) = (q 4, #, R) d 1(q 3, a) = (q 4, a, R) d(q 1, a) = (q 2, a, R) d(q 1, #) = (q 2, #, R) d(q 2, a) = (q 2, a, R) d(q 2, #) = (q 3, #, L) d(q 3, #) = (p 1, #, R) d(q 3, a) = (p 1, a, R) d(p 1, a) = (p 2, a, R) d(p 1, #) = (p 2, a, R) Mueve la cabeza lec/esc hasta la posición del siguiente blanco a la derecha. Definimos la máquina M 2 con F 2 = {p 2} con d 2(p 1, a) = (p 2, a, R) d 2(p 1, #) = (p 2, a, R) Escribe a en la posición de la cabeza lec/esc. Se representa por el símbolo a. con F = {p 2} Se mueve al siguiente blanco a la derecha y escribe una a.

Antes de R#R# a a Ejemplo a a Cabeza lec/esc Después de R#R# a a Cabeza lec/esc #

Otra forma de R# d(q, s) s # s=# q 1 (q 2, s, R) (q 2, #, R) q 2 (q 2, s, R) (q 3, #, L) q 3 (q 4, s, R) (q 4, #, R)

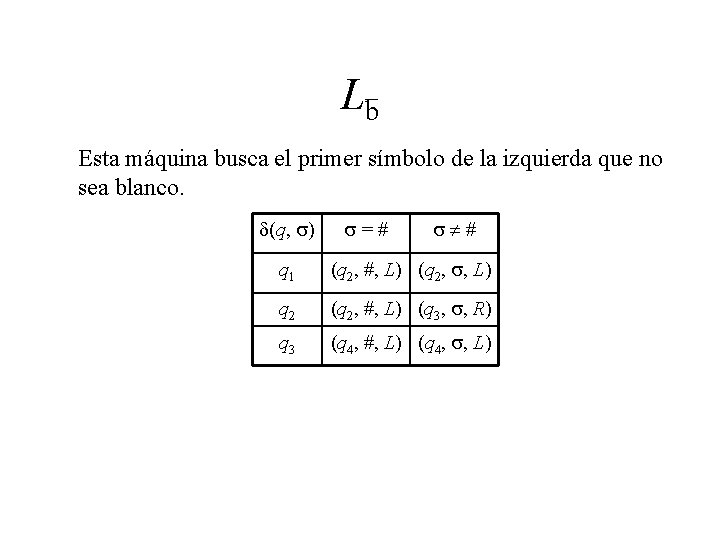
Lb Esta máquina busca el primer símbolo de la izquierda que no sea blanco. d(q, s) s=# s # q 1 (q 2, #, L) (q 2, s, L) q 2 (q 2, #, L) (q 3, s, R) q 3 (q 4, #, L) (q 4, s, L)

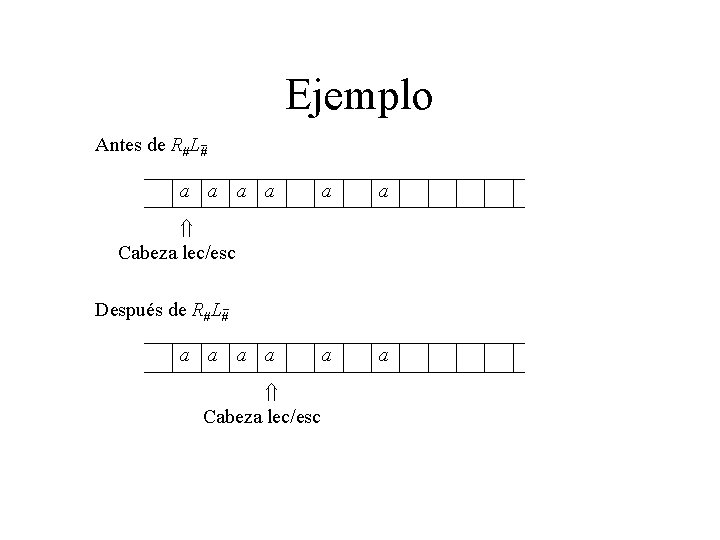
Ejemplo Antes de R#L# a a a a Cabeza lec/esc Después de R#L# a a Cabeza lec/esc

Otras máquinas útiles Escribe el símbolo a sobre la cinta y deja la cabeza sobre el símbolo d(q, s) s G q 1 (q 2, a, R) q 2 (q 2, s, L) La siguiente máquina termina en q 3 si el símbolo en la cinta es un blanco y termina en q 5 si es una a. Esta máquina representa una bifurcación y se representa mediante dos flechas. d(q, s) s=# s=a q 1 (q 2, #, L) (q 4, a, L) q 2 (q 3, #, R) (q 3, a, R) q 4 (q 5, #, R) (q 5, a, R) s=# s=a

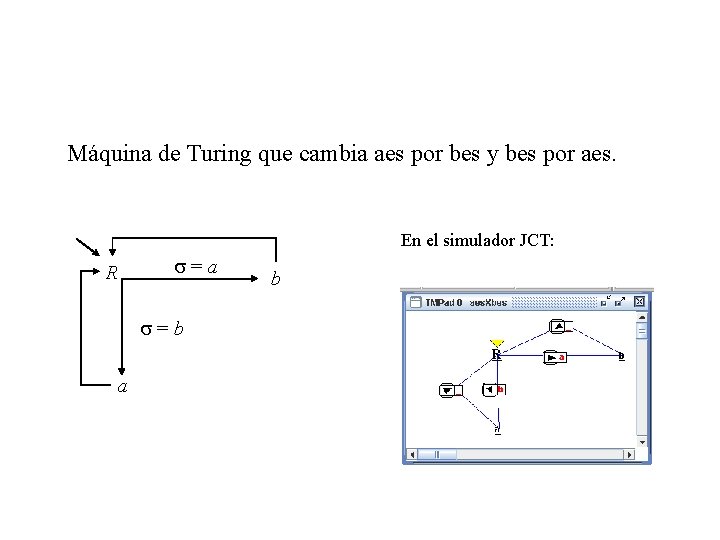
Máquina de Turing que cambia aes por bes y bes por aes. En el simulador JCT: R s=a s=b a b

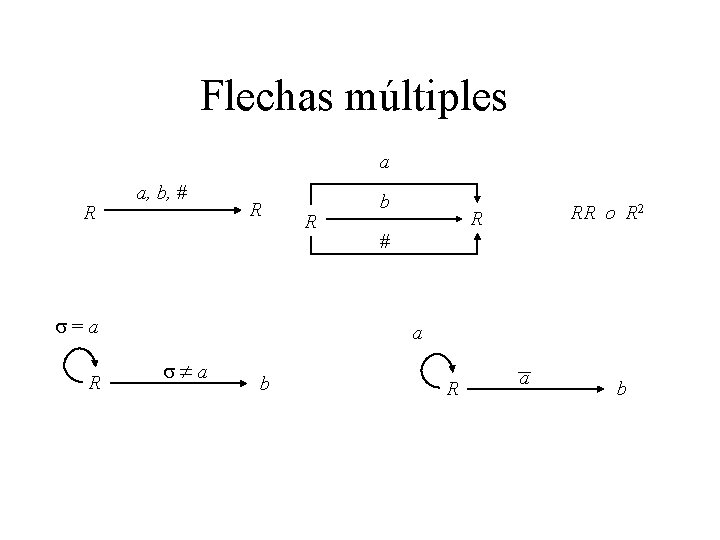
Flechas múltiples a R a, b, # R s=a R R b RR o R 2 R # a s a b R a b

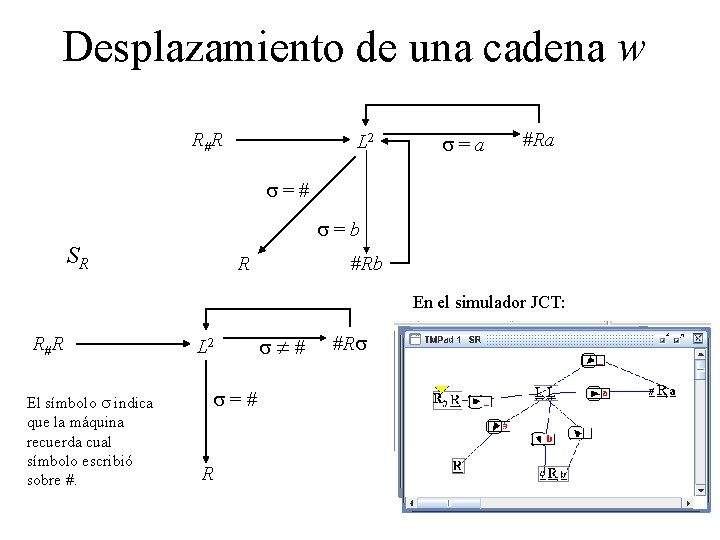
Desplazamiento de una cadena w R# R L 2 s=a #Ra s=# s=b SR R #Rb En el simulador JCT: R# R El símbolo s indica que la máquina recuerda cual símbolo escribió sobre #. L 2 s=# R s # #Rs

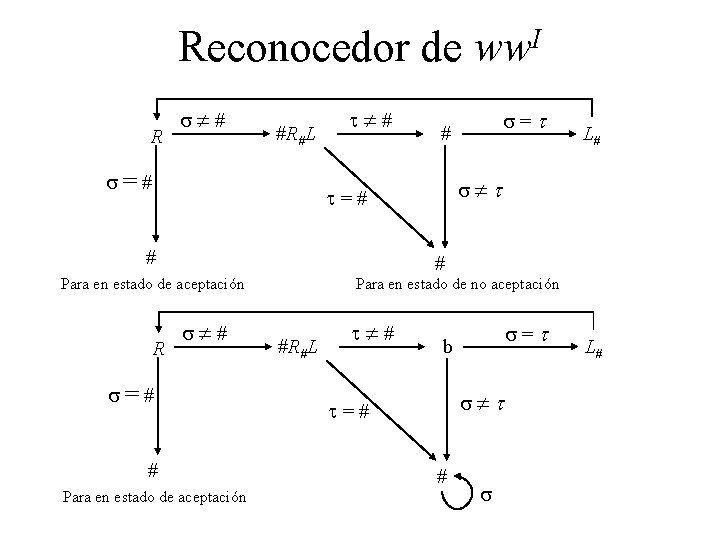
Reconocedor de R s # #R#L s=# t # L# s t # Para en estado de aceptación R s=t # t=# # I ww s # s=# # Para en estado de aceptación Para en estado de no aceptación #R#L t # s=t b s t t=# # s L#

Modificaciones de las máquinas de Turing Transiciones sin movimiento de la cabeza lec/esc. Modificar d: Q G {R, L} Por d: Q G {R, L, S} Donde S significa permanecer. Puede obtenerse con una máquina normal agregando d(q, s) = (p’, s’, R) y d(p’, t) = (p, t, L) t G

Cinta dividida en subceldas La cinta contiene múltiples caracteres. El movimiento de la cabeza dependerá del estado actual y de la n-tupla que represente el contenido actual. a a a b b a

Suma binaria El alfabeto estará formado por las ternas: (b, b, b) (0, 0, b) (0, 1, b) (1, 0, b) (1, 1, b) (0, 0, 0) (0, 1, 0) (1, 0, 0) (1, 1, 0) (0, 0, 1) (0, 1, 1) (1, 0, 1) (1, 1, 1) (b, b, 1) Primero buscará el extremo derecho mediante d(q 1, s) = (q 1, s, R) si s <> (b, b, b) d(q 1, s) = (q 2, s, L) si s = (b, b, b) además: d(q 2, (0, 0, b)) = (q 2, (0, 0, 0), L) d(q 3, (0, 0, b)) = (q 2, (0, 0, 1), L) d(q 2, (0, 1, b)) = (q 2, (0, 1, 1), L) d(q 3, (0, 1, b)) = (q 3, (0, 1, 0), L) d(q 2, (1, 0, b)) = (q 2, (1, 0, 1), L) d(q 3, (1, 0, b)) = (q 3, (1, 0, 0), L) d(q 2, (1, 1, b)) = (q 3, (0, 0, 0), L) d(q 3, (1, 1, b)) = (q 3, (1, 1, 1), L) d(q 2, (b, b, b)) = (q 4, (b, b, 0), S) d(q 3, (b, b, b)) = (q 2, (b, b, 1), S)

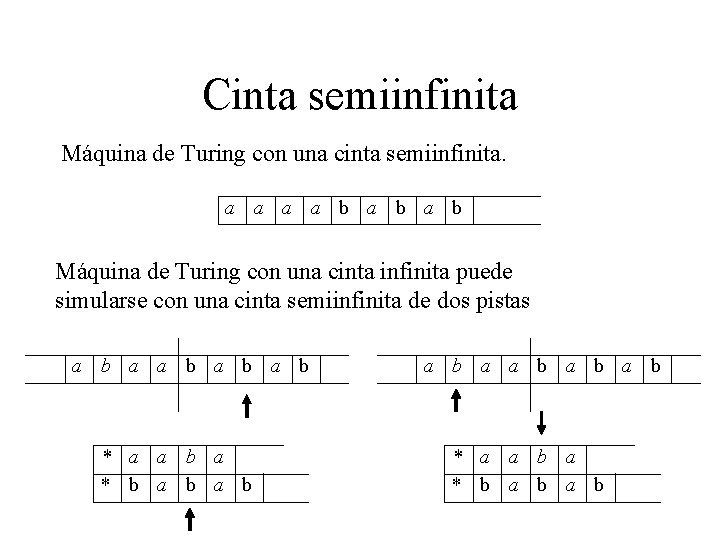
Cinta semiinfinita Máquina de Turing con una cinta semiinfinita. a a b a b Máquina de Turing con una cinta infinita puede simularse con una cinta semiinfinita de dos pistas a b a b a b * a a b a * b a b a b

Máquinas multicinta Contiene varias cintas independientes. En un solo movimiento, esta máquina de Turing 1. Cambia de estado dependiendo del estado actual y del contenido de las celdas de todas las cintas, que están analizando actualmente las cabezas lec/esc. 2. Escribe un nuevo símbolo en cada una de las celdas barridas por sus cabezas lec/esc. 3. Mueve cada una de las cabezas hacia la izquierda o hacia la derecha (de forma independiente al resto de las cabezas). d: Q Gn {L, R}n d(q, (s 1, s 2, s 3, . . . , sn)) = (p, (t 1, t 2, t 3, . . . , tn), (X 1, X 2, X 3, . . . , Xn))

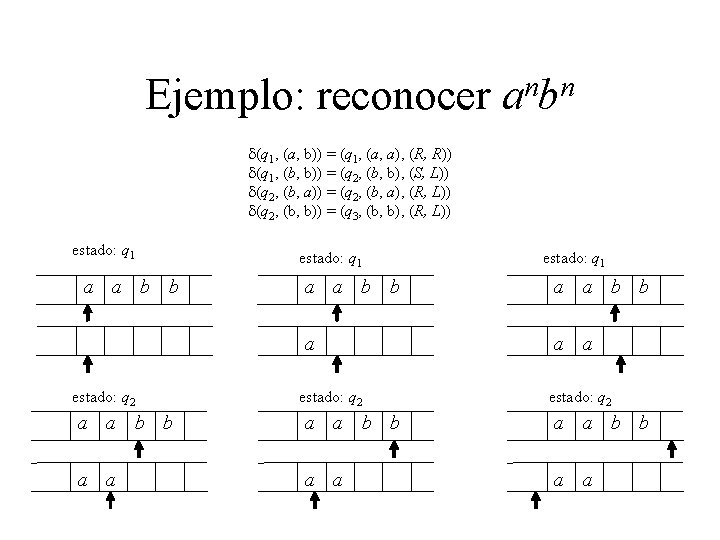
Ejemplo: reconocer n n ab d(q 1, (a, b)) = (q 1, (a, a), (R, R)) d(q 1, (b, b)) = (q 2, (b, b), (S, L)) d(q 2, (b, a)) = (q 2, (b, a), (R, L)) d(q 2, (b, b)) = (q 3, (b, b), (R, L)) estado: q 1 a a b b estado: q 2 estado: q 1 a a b b a a a estado: q 2 a a b b a a a

Máquina Universal de Turing una máquina Universal de Turing es una máquina que a partir de una descripción de una máquina de Turing M y una cadena de entrada w, simula el comportamiento de M sobre la cadena w. Suponemos que Q = {q 1, q 2, . . . , qn} donde q 1 es el estado inicial y q 2 es el único estado de aceptación. Además G = {s 1, s 2, . . . , sm} donde s 1 es el símbolo blanco. Codificamos M de la siguiente manera representamos q 1 por 1 representamos q 2 por 11, etc representamos s 1 por 1 representamos s 2 por 11, etc representamos L por 1 y representamos R por 11 Ejemplo: d(q 3, s 1) = (q 4, s 3, L) 011101001111010

Máquina Universal de Turing La máquina de Turing Universal Mu consta de tres cintas 1 er cinta – la codificación de M en uno y ceros. 2 a. cinta – la codificación del contenido de la cinta de M en unos y ceros. 3 a. cinta – la codificación del estado actual codificado de M.

Problema de la parada El problema de la parada o problema de la detención para máquinas de Turing es el ejemplo de problema irresoluble más conocido. Consiste en determinar si una máquina de Turing se detendrá con cierta entrada, o bien quedará en un ciclo infinito. Este fue el primer problema que se demostró formalmente que no tenía solución.

Problema de la parada Definición Sea M una máquina de Turing arbitraria con un alfabeto de entrada Σ. Sea. ¿Puede decidirse si la máquina M se detendrá con la entrada w? Demostración Para demostrarlo, supongamos que el problema de la parada tiene solución, es decir, supondremos que existe una máquina de Turing que es capaz de determinar si otra máquina de Turing para con una entrada determinada.

Problema de la parada Consideremos una máquina de Turing P, que recibe como entrada una máquina de Turing M y una cadena w codificadas en la cinta y una a continuación de la otra (Mw), y que se encarga de ejecutar M sobre la cadena w. La máquina P parará y aceptará la entrada si M para con w, y parará y rechazará la entrada si M no para con w.

Modificamos la máquina P, creando una máquina P' equivalente. Esta máquina no parará si M para con w, y parará si M no para con w.

Ahora crearemos una máquina D, cuya función es la siguiente. Recibe una máquina M, la pasa por una máquina que se encarga de copiar la máquina M a continuación. Por lo tanto, a la salida de la máquina copia, la cinta contendrá MM (la codificación de la máquina repetida). A continuación, D coge este resultado y lo pasa a través de P'. Con esto intentamos decidir si la máquina M para con la entrada M. Es decir, si M para con la entrada M, entonces D no para, y si M no para con la entrada M, entonces D para.

Por último, tomaremos una máquina D (denominaremos SD), y le aplicaremos como entrada una máquina D. SD aplica como entrada a la máquina que recibe, la misma máquina. Por lo tanto, esta máquina en principio parará si D no para con entrada D, y no parará si D para con entrada D. Pero si SD no para y si D para con entrada D, sabiendo que D=SD, llegamos a una contradicción, por que aplicar D a SD debería dar como resultado lo mismo que aplicar D sobre D. Del mismo modo para el otro caso. Por lo tanto, el problema de la parada no tiene solución. Obtenido de "http: //es. wikipedia. org/wiki/Problema_de_la_parada"

Lenguajes recursivamente enumerables Un lenguaje L sobre un alfabeto S se dice que es recursivamente enumerable si es aceptado por una máquina de Turing. Un lenguaje L es recursivo si L es recursivamente enumerable y hay alguna máquina de Turign que para sobre todas las entradas que acepta L.

Máquina para reconocer un lenguaje regular Sea M = (Q, S, s, F, d), un autómata finito determinista, Se puede construir una máquina de Turing que reconozca el lenguaje reconocido por M, M’ = (Q’, S’, G, s’, #, F’, d’), donde Q’ = Q {q’} S’ = S G = S {#} F’ = {q’} d’(q, s) = (d’(q, s), s, R) para todo q Q y s S d’(q, #) = (q, #, S) para todo q Q

Gramáticas no restringidas Una gramática no restringida (también se conoce como una gramática estructurada por frases) es una 4 -tupla G = (N, S, S, P), donde N es el alfabeto de símbolos no terminales S es el alfabeto de símbolos terminales S N es el símbolo inicial P es un conjunto de producciones de la forma a b, donde a (N S)+ u b (N S)* (es decir, P (N S)+ (N S)* y es un conjunto finito)

Ejemplo S a. SBC | a. BC CB BC a. B ab b. B bb b. C bc c. C cc La producción CB BC intercambia los no terminales B y C, obteniendo una cadena de la forma an. Bn. Cn. Las producciones a. B ab y b. B bb transforman toda B en b, obteniendo anbn. Cn. Las producciones b. C bc y c. C cc transforman toda C en c, obteniendo anbncn

Ejemplo S ACa. B Ca aa. C CB DB | E a. D Da AD AC a. E Ea AE e A y B actúan como marcadores de final de la cadena de aes. C se desplaza a la derecha al duplicarse el número de aes hasta que está junto a B, entonces se transforma en D. D se desplaza hacia la izquierda hasta que encuentra una A, y entonces se convierte en C. Cuando CB se reemplaza por E, termina la generación de aes. Entonces E se desplaza a la izquierda hasta que encuentra la A, momento en el cual se elimina AE. Lenguaje generado:

La Jerarquía de Chomsky Tipo Language Autómata Normas de producción de gramáticas 0 recursivamente enumerable (LRE) Máquina de Turing (MT) Sin restricciones 1 dependiente del contexto (LSC) Autómata linealmente acotado αAβ → αγβ 2 independiente del contexto (LLC) Autómata con pila A→γ A → a. B 3 regular (RL) Autómata finito A→a