Turing Machines Part One Intro CSCI 432 Computer

Turing Machines Part One - Intro CSCI 432 Computer Science Theory

Alan Turing Ø 1912 - 1954 Ø English mathematician, computer scientist, logician, cryptanalyst Ø "father of computer science theory" Ø code breaker for British in WW 2

Human Computer If a human were to use pencil and paper to solve problems, what fundamental steps would he use? v erasing a symbol on paper and replacing it with another symbol v the symbol to write would depend on ü the symbol observed by the pencil ü the state of mind of the computer Theory of Computing by Kinber & Smith, page 121

Turing Machine Finite Automata a) current state b) next symbol on the tape c) next state based on current state and next symbol Turing Machine additions d) move the tape backwards e) rewrite the current symbol

Sequence, Selection, Iteration v Sequence o the read head can be moved forward v Selection o the states can transition based on the state and the symbol v Iteration o the read head can move backward Thus, a Turing Machine has all the elements of an imperative programming language. Theory of Computing by Kinber & Smith, page 122

Church-Turing thesis Every computer algorithm can be implemented as a Turing Machine.

Tape q Just like a FA or PDA, the tape is loaded with input symbols before the program is run. q The tape has a left border, marked with > § if it sees >, it automatically moves right one space q The tape has no right border (infinite memory). q At the end of the input symbols is a blank space.

States q Just like a FA, the current symbol and the current state determine the next state. o the next state might be the current state q A TM has additional actions: o rewrite the current symbol o move forward o move backwards q Unlike a FA, a TM does not terminate at the end of input. o Special states terminate the program

Formal Definition S ∑ s∈S H⊆S δ set of States alphabet, contains > and blank initial state set of Halting States transition function (deterministic)

Formal δ Notation o This formal definition of the delta function is similar to the notation we used for PDA transitions. o We need to know § § current state current symbol next state new symbol o Examples o ( (q, a), (p, b) ) When in state q reading symbol 'a', write a 'b' and change state to p. o ( (s, >), (s, R) ) When in state s and reading left end of tape, keep state s and go right

Formal δ Notation example 1 TM to erase a tape full of the symbol 'a'. 1. ( (s, -), (h, -) ) 2. ( (s, a), (q, -) ) 3. ( (q, -), (s, R) ) "-" is my way to indicate a blank Computations: s q s q s h > > > > a - a a a a a - - start after state s and initial tape applying rule 2 applying rule 3 after applying rule 1 Theory of Computing by Kinber & Smith, page 124

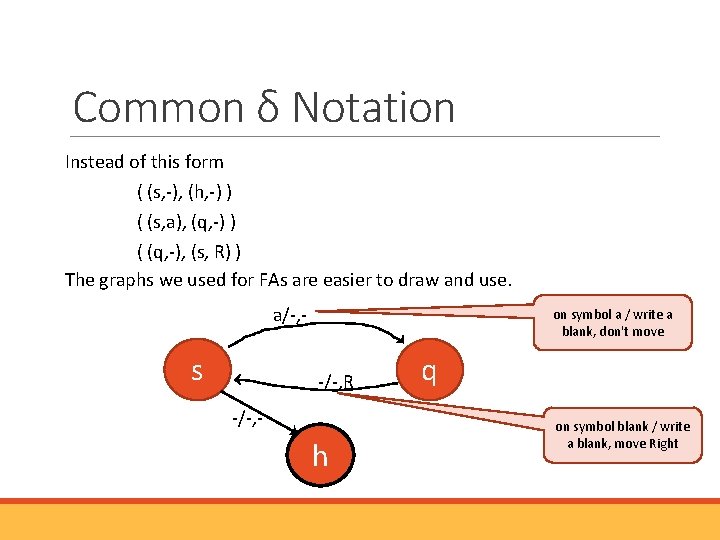
Common δ Notation Instead of this form ( (s, -), (h, -) ) ( (s, a), (q, -) ) ( (q, -), (s, R) ) The graphs we used for FAs are easier to draw and use. a/-, - s on symbol a / write a blank, don't move -/-, R -/-, - h q on symbol blank / write a blank, move Right

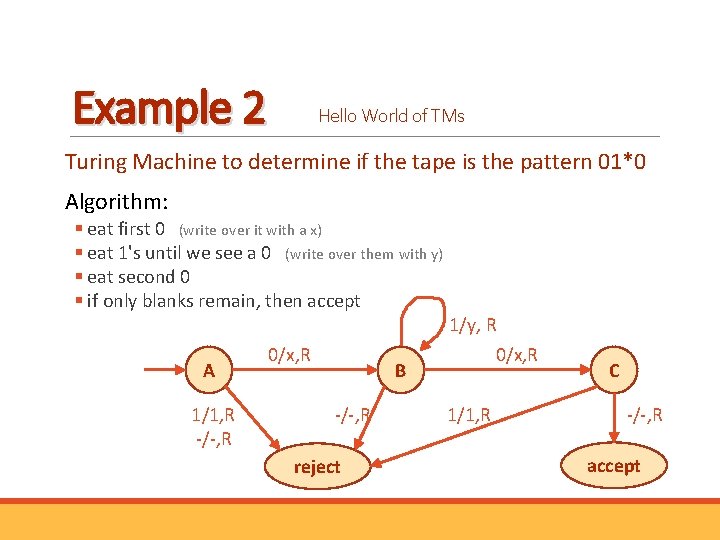
Example 2 Hello World of TMs Turing Machine to determine if the tape is the pattern 01*0 Algorithm: § eat first 0 (write over it with a x) § eat 1's until we see a 0 (write over them with y) § eat second 0 § if only blanks remain, then accept A 1/1, R -/-, R 0/x, R B -/-, R reject 1/y, R 0/x, R 1/1, R C -/-, R accept

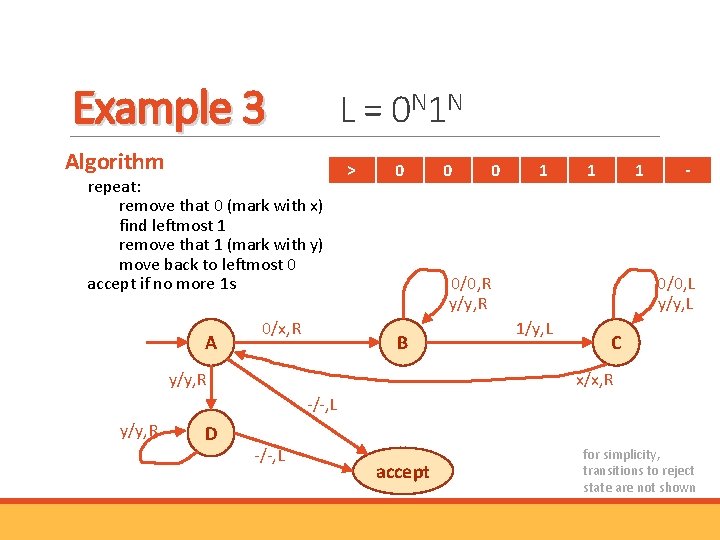
Example 3 L = 0 N 1 N Algorithm repeat: remove that 0 (mark with x) find leftmost 1 remove that 1 (mark with y) move back to leftmost 0 accept if no more 1 s A 0/x, R > 0 0 0 1 1 1 0/0, R y/y, R B y/y, R - 0/0, L y/y, L 1/y, L C x/x, R -/-, L y/y, R D -/-, L accept for simplicity, transitions to reject state are not shown

Next Classes v more basic Turing Machines v creating Turing Machines v subroutines v varieties of Turing Machines