CS 3240 Languages and Computation Turing Machine Turing

CS 3240: Languages and Computation Turing Machine

Turing and Turing Machine Alan Turing (1912– 1954), British mathematician/engineer. In 1936, Turing introduced his abstract model for computation in his article “On Computable Numbers, with an application to the Entscheidungsproblem” Near the same time, Alonzo Church published similar ideas and results. Turing machine is the ultimate model of computation.

Comparison of TM and FA TM has tape you can read from and write to Read-write head can be moved in either direction Tape is infinite Accept and reject states take effect immediately

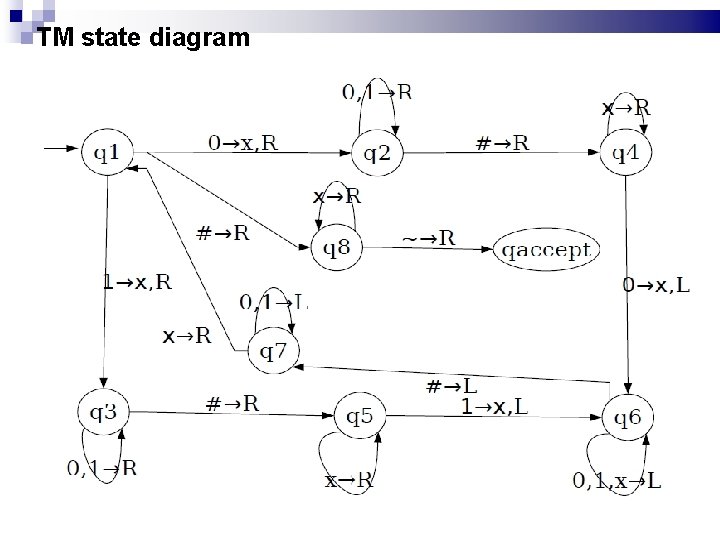
Example I Language { w#w | w {0, 1}* } How can we design a Turing machine to test its membership? Zig-zag across tape to corresponding positions on either side of # to check whether they contain same symbol. If not or if no # found, reject. Cross off symbols as they are checked When all symbols to the left of # are crossed off, if anything remain to the right o #, reject; otherwise, accept. Example: test on string 011001$011001

Formal definition of TM Definition: A Turing machine is a 7 -tuple (Q, , q 0, qaccept, qreject), where Q, , and are finite sets and � Q is the set of states, is the input alphabet not containing the special blank symbol ~ is tape alphabet, where {~} , : Q Q {L, R} is the transition function,

Formal definition of a TM Definition: A Turing machine is a 7 -tuple (Q, , q 0, qaccept, qreject), where Q, , and are finite sets and • q 0 Q is the start state, • qaccept Q is the accept state, and • qreject Q is the reject state, where qreject qaccept

More on Transition Function Q = set of states, = tape alphabet : Q Q {L, R} Given: The current internal state Q The symbol on the current tape cell Then tells us what the TM does: Changes to new internal state Q Either writes new symbol Or moves one cell left or right

Computing with TM M receives input w = w 1 w 2…wn * on leftmost n squares of tape Rest of tape is blank (all ~ symbols) Head position begins at leftmost square of tape Computation follows rules of Head never moves left of leftmost square of the tape If says to move L, head stays put!

Completing computation Continue following transition rules until M reaches qaccept or qreject Halt at these states May never halt if machine never reaches one of these states!

Turing machine notation (qi, b)=(qk, c, D), where D = L or R, is represented by the following transition b c, D qi qk In the special case where (qi, b)=(qk, b, D), i. e. , the tape is unchanged, the right-hand side will just display the direction

Revisiting Example I (q 1, 0) = (q 2, x, R); (q 2, 0) = (q 2, 0, R); (q 2, 1) = (q 2, 1, R); (q 2, #) = (q 4, #, R) (q 4, x)=(q 4, x, R); (q 4, 0)=(q 6, x, L) (q 1, 1) = (q 3, x, R) (q 3, 0) = (q 3, 0, R); (q 3, 1) = (q 3, 1, R); (q 3, #) = (q 5, #, R) (q 5, x)=(q 5, x, R); (q 5, 1)=(q 6, x, L) (q 6, a)=(q 6, a, L) for a=0, 1, or x (q 6, #)= (q 7, #, L); (q 7, 0)= (q 7, 0, L); (q 7, 1)= (q 7, 1, L); (q 7, x)= (q 1, x, R) (q 1, #) = (q 8, #, R); (q 8, x) = (q 8, x, R); (q 8, ~) = (qaccept, ~, R)

TM state diagram

Example E={#x 1#x 2#x 3…#xn | xi {0, 1}* and xi≠xj for i ≠ j} Basic idea: Compare each pair of (xi , xj) by zigzagging. Use special marks to replace # to indicate which pair of (xi , xj) is being compared Must take care special cases such as n=0, n=1, missing #, etc.

Question How to detect whether we have reached leftmost cell? Alternative 1: If leftmost cell marked by special symbol, then easy Alternative 2: Use special property that TM “stays put” at left-most cell by replacing cell with special symbol and then recover

TM configurations The configuration of a Turing machine is the current setting Current state Current tape contents Current tape location Notation uqv Current state = q Current tape contents = uv Only ~ symbols after last symbol of v Current tape location = first symbol of v

Configuration C 1 yields C 2 if the TM can legally go from C 1 to C 2 in one step a, b and u, v * uaqibv yields uqkacv Assume if (qi, b)=(qk, c, L) uaqibv yields uacqkv if (qi, b)=(qk, c, R)

Configuration C 1 yields C 2 Special cases if head is at beginning or end of tape yields uqjacv if (qi, b)=(qk, c, L) uaqibv yields uacqkv if (qi, b)=(qk, c, R) Special case: uaqibv~ yields qkcv~ if (qi, b)=(qk, c, L) and tape head is at beginning of tape

Special configurations Start configuration q 0 w Halting configurations Accepting configuration: uqacceptv Rejecting configuration: uqrejectv u, v *

Strings accepted by a TM A Turing machine M accepts input sequence w if a sequence of configurations C 1, C 2, …, Ck exist, where – – – C 1 is the start configuration of M on input w each Ci yields Ci+1 for i = 1, 2, …, k-1 Ck is an accepting configuration

Language of a TM The language of M, denoted L(M), is L(M) = {w | M accepts w} A language is called Turing-recognizable if some Turing machine recognizes it

Deciders A Turing machine is called a decider if every string in * is either accepted or rejected A language is called Turing-decidable if some Turing machine decides it These languages are often just called decidable