Efficiency and Flexibility of Jagged Arrays Geir Gundersen

Efficiency and Flexibility of Jagged Arrays Geir Gundersen Department of Informatics University of Bergen Norway Joint work with Trond Steihaug

Objectives Efficiency of linear and jagged arrays for several numerical linear algebra algorithms. Flexibility of linear and jagged arrays for LU factorization on a banded matrix. Jagged versus Multidimensional arrays on row-oriented algorithms in C#. Compare these algorithms on only two platforms using the languages C, C# and Java.

Basic Storage Schemes for Matrices Storage Schemes: Multidimensional Arrays Jagged Arrays Linear Arrays

Algorithms Matrix Vector product LU Decomposition (LU=PA) 3 D Element Sum/Voxel Sum

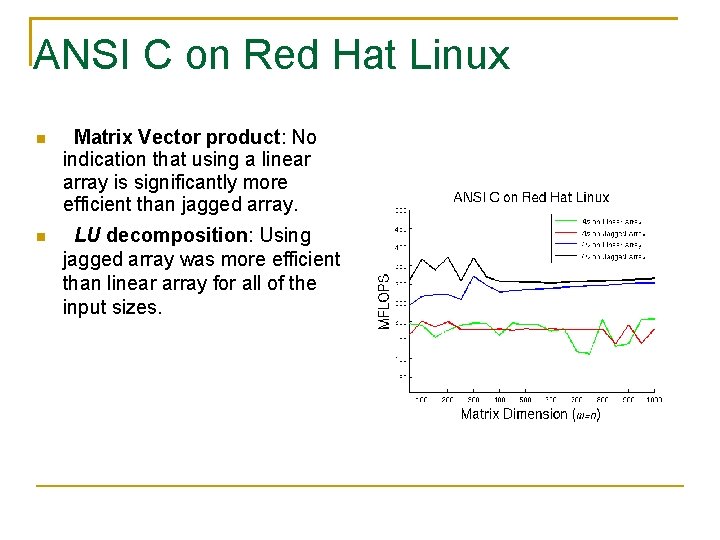
ANSI C on Red Hat Linux Matrix Vector product: No indication that using a linear array is significantly more efficient than jagged array. LU decomposition: Using jagged array was more efficient than linear array for all of the input sizes.

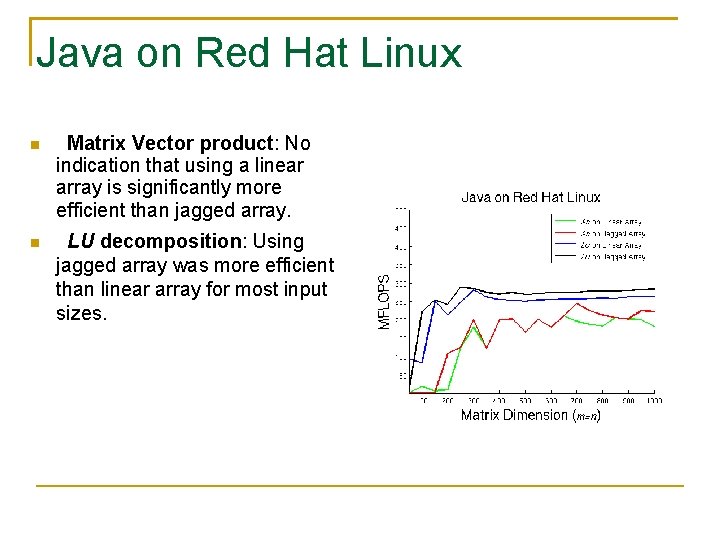
Java on Red Hat Linux Matrix Vector product: No indication that using a linear array is significantly more efficient than jagged array. LU decomposition: Using jagged array was more efficient than linear array for most input sizes.

Java on Windows XP Matrix Vector product: No indication that using a linear array is significantly more efficient than jagged array. LU decomposition: Using jagged array was more efficient than linear array for most input sizes.

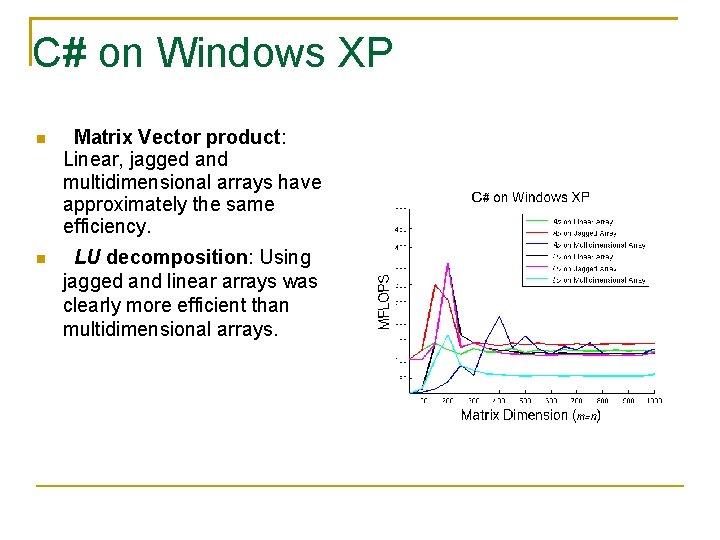
C# on Windows XP Matrix Vector product: Linear, jagged and multidimensional arrays have approximately the same efficiency. LU decomposition: Using jagged and linear arrays was clearly more efficient than multidimensional arrays.

Jagged versus Multidimensional arrays in row-oriented algorithms in C#Jagged arrays are for row-oriented algorithms approximately 25% more efficient than multidimensional arrays. Minor limitations in the current JIT compiler regarding the elimination of array bounds check for multidimensional arrays. Column, diagonally or random traversel with jagged arrays performs poorly compared to multidimensional arrays.

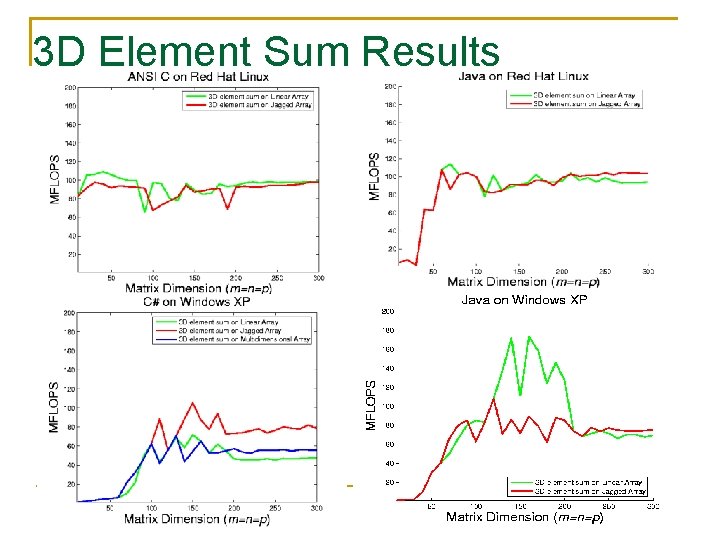
3 D Element Sum Results

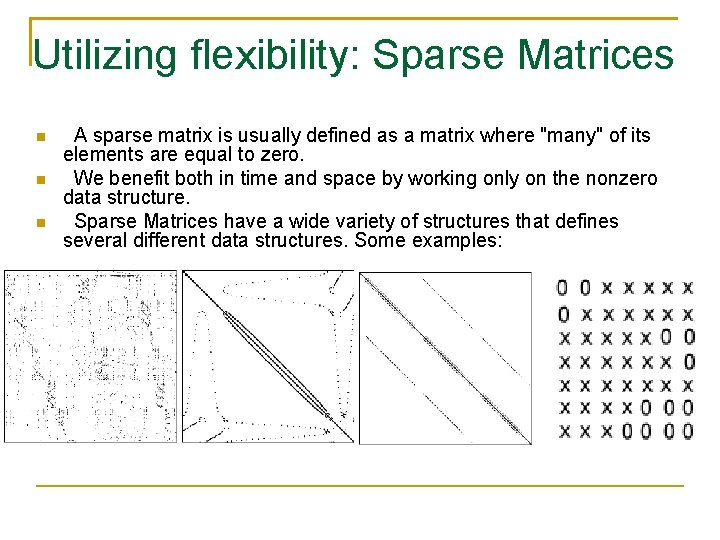
Utilizing flexibility: Sparse Matrices A sparse matrix is usually defined as a matrix where "many" of its elements are equal to zero. We benefit both in time and space by working only on the nonzero data structure. Sparse Matrices have a wide variety of structures that defines several different data structures. Some examples:

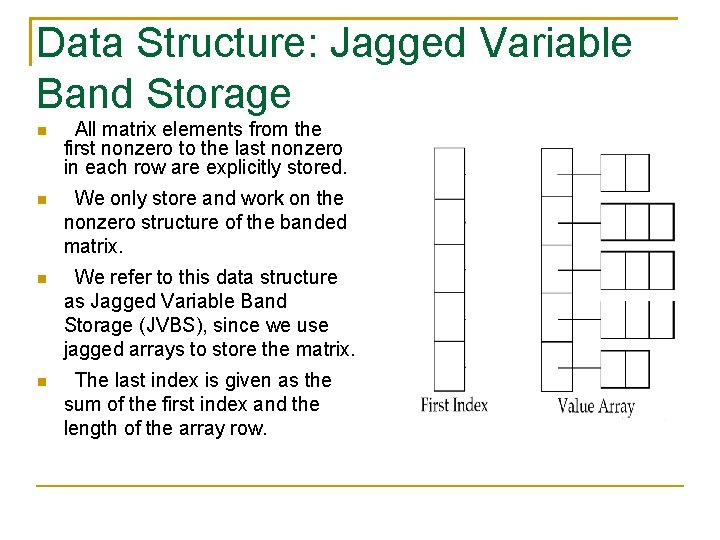
Data Structure: Jagged Variable Band Storage All matrix elements from the first nonzero to the last nonzero in each row are explicitly stored. We only store and work on the nonzero structure of the banded matrix. We refer to this data structure as Jagged Variable Band Storage (JVBS), since we use jagged arrays to store the matrix. The last index is given as the sum of the first index and the length of the array row.

LU Decomposition on Variable Band Storage (VBS): LU decomposition with row partial pivoting (LU=PA) on VBS does not guarantee that the nonzero structure is preserved, i. e. we can get new entries (fillins) in the data structure. An LU decomposition of a sparse matrix consist of a symbolic and a numerical phase. In general, no symbolic phase can predict fill-ins in since the pivot choices are based on numerical values, during the decomposition.

Fill-Ins Issues Two approaches: Resize the whole data structure for each row that has new fill-ins. Resize each row that has new fill-ins. The first approach must be done using linear or multidimensional arrays. The second approach is clearly the most efficient using jagged arrays. We do not have any overall loss using jagged arrays. It is therefore the preferred choice rather than linear and multidimensional arrays.

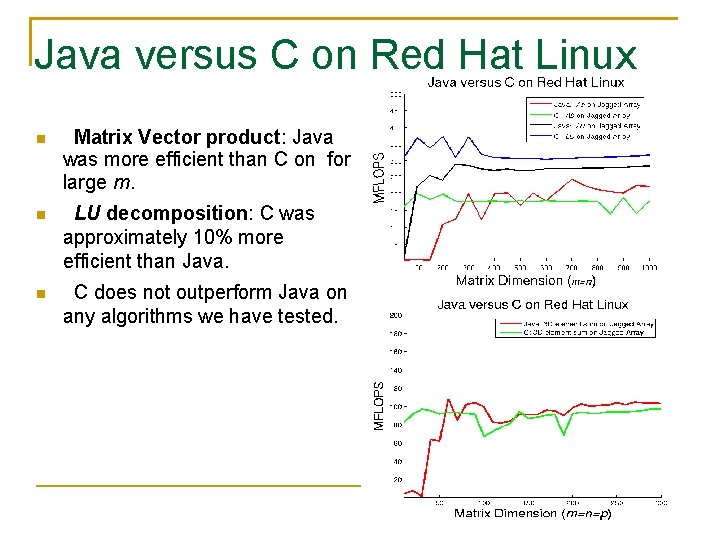
Java versus C on Red Hat Linux Matrix Vector product: Java was more efficient than C on for large m. LU decomposition: C was approximately 10% more efficient than Java. C does not outperform Java on any algorithms we have tested.

Not Covered Jagged arrays have poor performance on column-oriented algorithms. In [G. Gundersen and T. Steihaug. Data Structures in Java for Matrix Computation. Concurrency and Computation: Practice and Experience Volume 16, Issue 8, Pages 735 -815 (July 2004). ] it is shown for several matrix multiplication algorithms the impact of column-oriented algorithms for jagged arrays in Java. It is clear from those numerical results that column-oriented algorithms can be multiple times slower than their row-oriented versions. That Java also is as fast as C++ for some algorithms is reported in [Performance test shows Java as fast as C++, Carmine Mangione, in Java. World, February 1998].

Concluding Remarks The numerical testing shows insignificant differences in performance (less than 10%) between Java versus C# and Java versus C. Jagged arrays on row-oriented algorithms in C, Java and C# are competitive with linear arrays, despite non-contiguously memory layout. Our observations on the performance of row-oriented algorithms using jagged arrays are important and indicate that flexibility and efficiency are not mutually exclusive.