Describing Data Using Numerical Measures Mean The mean

Describing Data Using Numerical Measures

Mean The mean is a numerical measure of the center of a set of quantitative measures computed by dividing the sum of the values by the number of values in the data set.

Population Mean where: = population mean (mu) N = number of data values xi = ith individual value of variable x

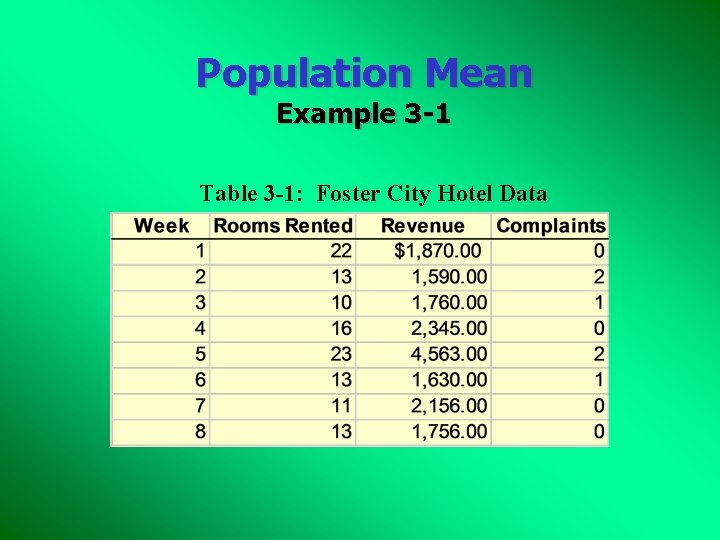
Population Mean Example 3 -1 Table 3 -1: Foster City Hotel Data

Population Mean Example 3 -1 The population mean for the number of rooms rented is computed as follows:

Sample Mean where: = sample mean (pronounced “x-bar”) = sample size xi = ith individual value of variable x n

Sample Mean Housing Prices Example {xi} = {house prices} = {$144, 000; 98, 000; 204, 000; 177, 000; 155, 000; 316, 000; 100, 000}

Median The median is the center value that divides data that have been arranged in numerical order (i. e. an ordered array) array into two halves.

Median Housing Prices Example {xi} = {house prices} = {$144, 000; 98, 000; 204, 000; 177, 000; 155, 000; 316, 000; 100, 000} Ordered array: $98, 000; 100, 000; 144, 000; 155, 000; 177, 000; 204, 000; 316, 000 Middle Value Median = 155, 000

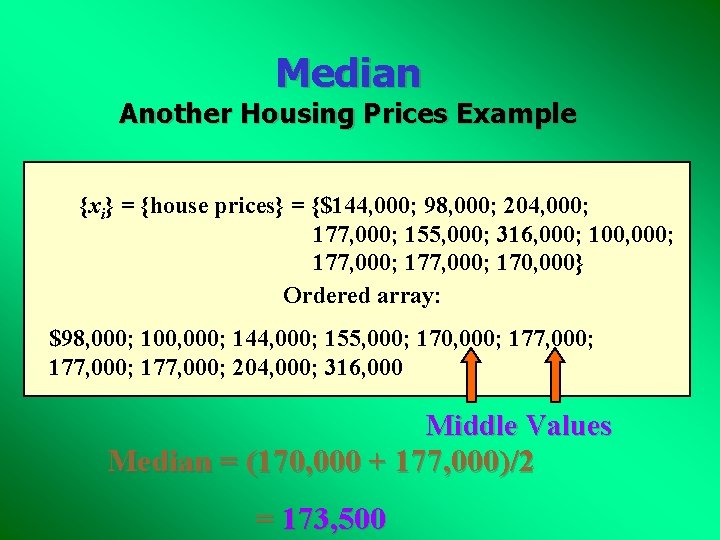
Median Another Housing Prices Example {xi} = {house prices} = {$144, 000; 98, 000; 204, 000; 177, 000; 155, 000; 316, 000; 100, 000; 177, 000; 170, 000} Ordered array: $98, 000; 100, 000; 144, 000; 155, 000; 170, 000; 177, 000; 204, 000; 316, 000 Middle Values Median = (170, 000 + 177, 000)/2 = 173, 500

Skewed Data 4 Right-skewed data: Data are right skewed if the mean for the data is larger than the median. 4 Left-skewed data: Data are left skewed if the mean for the data is smaller than the median.

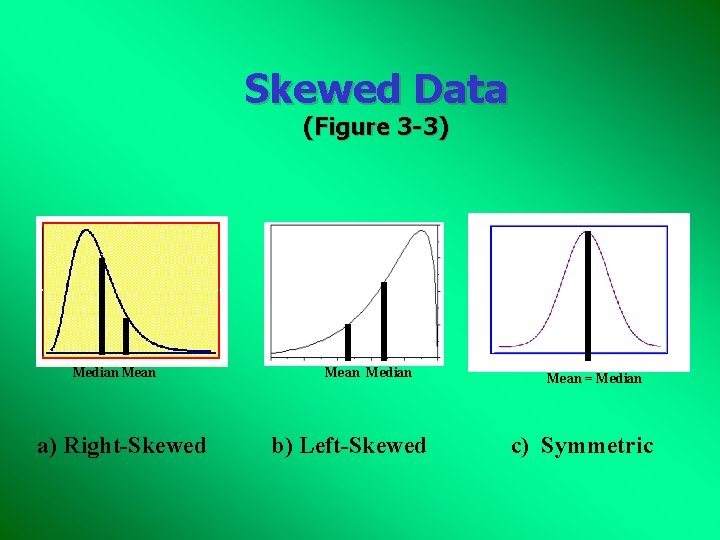
Skewed Data (Figure 3 -3) Median Mean a) Right-Skewed Mean Median b) Left-Skewed Mean = Median c) Symmetric

Percentiles The pth percentile in a data array is a value that divides the data into two parts. The lower segment contains at least p% and the upper segment contains at least (100 - p)% of the data. The median is the 50 th percentile.

Quartiles in a data array are those values that divide the data set into four equal-sized groups. The median corresponds to the second quartile.

Measures of Variation A set of data exhibits variation if all of the data are not the same value.

Range The range is a measure of variation that is computed by finding the difference between the maximum and minimum values in the data set. R = Maximum Value - Minimum Value

Interquartile Range The interquartile range is a measure of variation that is determined by computing the difference between the first and third quartiles. Interquartile Range = Third Quartile - First Quartile

Variance & Standard Deviation The population variance is the average of the squared distances of the data values from the mean. The standard deviation is the positive square root of the variance.

Population Variance where: = population mean N = population size 2 = population variance (sigma squared)

Population Variance (Bryce Lumber Example)

Population Standard Deviation (Bryce Lumber Example)

Sample Variance where: = sample mean n = sample size s 2 = sample variance

Sample Standard Deviation where: = sample mean n = sample size s = sample standard deviation

The Empirical Rule If the data distribution is bell-shaped, then the interval: contains approximately 68% of the values in the population or the sample contains approximately 95% of the values in the population or the sample contains virtually all of the data values in the population or the sample

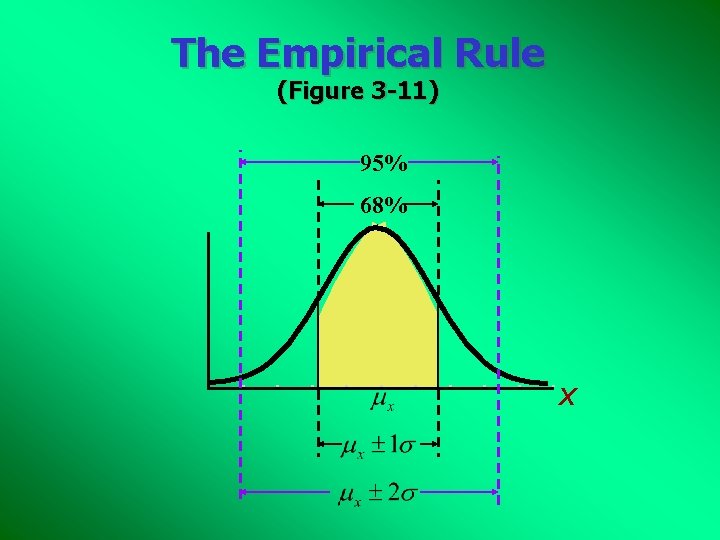
The Empirical Rule (Figure 3 -11) 95% 68% X

Tchebysheff’s Theorem Regardless of how the data are distributed, at least (1 - 1/k 2) of the values will fall within k = 1 standard deviations of the mean. For example: At least (1 - 1/12) = 0% of the values will fall within k=1 standard deviation of the mean ä At least (1 - 1/22) = 3/4 = 75% of the values will within k=1 standard deviation of the mean ä ä At least (1 - 1/32) = 8/9 = 89% of the values will within k=1 standard deviation of the mean fall

6 Sigma Quality 4 Specification for a quality characteristic is six standard deviation away from the mean of the process distribution. 4 Translates into process output that does not meet specifications two out of one billion times.

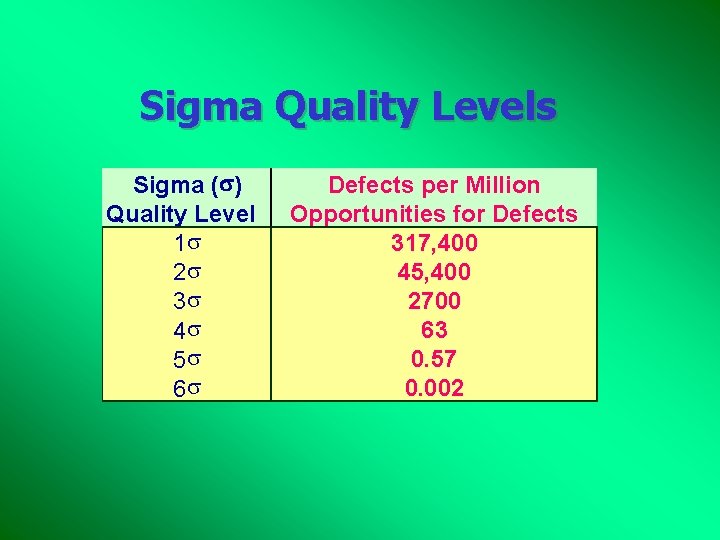
Sigma Quality Levels Sigma ( ) Quality Level 1 s 2 s 3 s 4 s 5 s 6 s Defects per Million Opportunities for Defects 317, 400 45, 400 2700 63 0. 57 0. 002

Sigma Quality Level Concepts Sigma ( ) Quality Level 1 s 2 s 3 s 4 s 5 s 6 s 7 s Equated to Relative Area Floor space of a typical factory Floor space of a typical supermarket Floor space of a small hardware store Floor space of a typical living room Area under a typical desk telephone Top surface of a typical diamond Point of a sewing needle

Standardized Data Values A standardized data value refers to the number of standard deviations a value is from the mean. The standardized data values are sometimes referred to as zscores.

Standardized Data Values STANDARDIZED SAMPLE DATA where: x = original data value = sample mean s = sample standard deviation z = standard score