Similarity and Dissimilarity l Similarity Numerical measure of

Similarity and Dissimilarity l Similarity – Numerical measure of how alike two data objects are. – Is higher when objects are more alike. – Often falls in the range [0, 1] l Dissimilarity – Numerical measure of how different are two data objects – Lower when objects are more alike – Minimum dissimilarity is often 0 – Upper limit varies l Proximity refers to a similarity or dissimilarity © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 1

Similarity/Dissimilarity for Simple Attributes p and q are the attribute values for two data objects. © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 2

Euclidean Distance l Standardization is necessary, if scales differ. © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 3

Minkowski Distance l Minkowski Distance is a generalization of Euclidean Distance © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 4

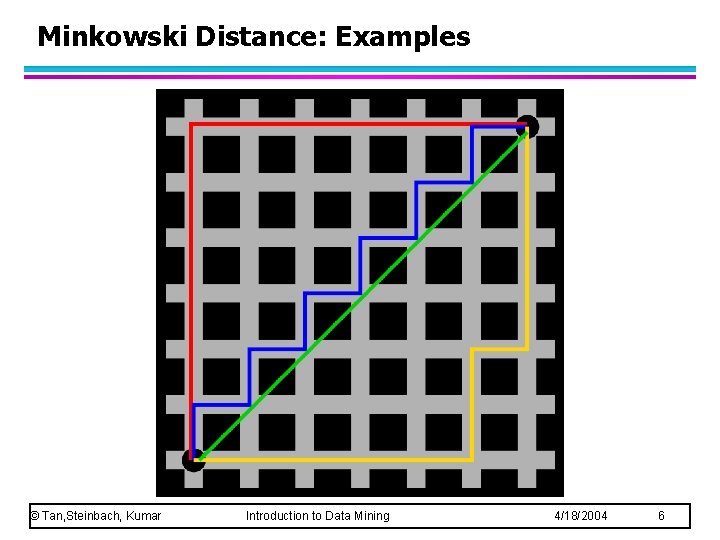
Minkowski Distance: Examples l r = 1. City block (Manhattan, taxicab, L 1 norm) distance. – A common example of this is the Hamming distance, which is just the number of bits that are different between two binary vectors l r = 2. Euclidean distance l r . “supremum” (Lmax norm, L norm) distance. – This is the maximum difference between any component of the vectors l Do not confuse r with n, i. e. , all these distances are defined for all numbers of dimensions. © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 5

Minkowski Distance: Examples © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 6

Common Properties of a Distance l Distances, such as the Euclidean distance, have some well known properties. 1. d(p, q) 0 for all p and q and d(p, q) = 0 only if p = q. (Positive definiteness) 2. 3. d(p, q) = d(q, p) for all p and q. (Symmetry) d(p, r) d(p, q) + d(q, r) for all points p, q, and r. (Triangle Inequality) where d(p, q) is the distance (dissimilarity) between points (data objects), p and q. l A distance that satisfies these properties is a metric © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 7

Common Properties of a Similarity l Similarities, also have some well known properties. 1. s(p, q) = 1 (or maximum similarity) only if p = q. 2. s(p, q) = s(q, p) for all p and q. (Symmetry) where s(p, q) is the similarity between points (data objects), p and q. © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 8

Similarity Between Binary Vectors l l Simple Matching Jaccard Coefficients Cosine similarity Correlation See IDM section 2. 4 for details © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 9