Numerical Descriptive Measures Chapter 2 Borrowed from http

Numerical Descriptive Measures Chapter 2 Borrowed from http: //www 2. uta. edu/infosys/amer/courses/3 321%20 ppts/c 3. ppt

Chapter Topics n Measures of central tendency n Mean, median, mode, midrange n Quartiles n Measure of variation n n Shape n n Range, interquartile range, variance and Standard deviation, coefficient of variation Symmetric, skewed (+/-) Coefficient of correlation

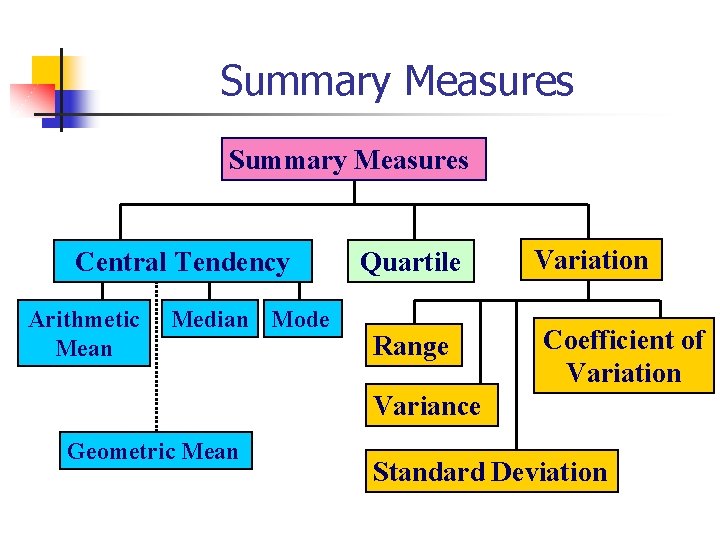
Summary Measures Central Tendency Arithmetic Mean Median Mode Quartile Range Variation Coefficient of Variation Variance Geometric Mean Standard Deviation

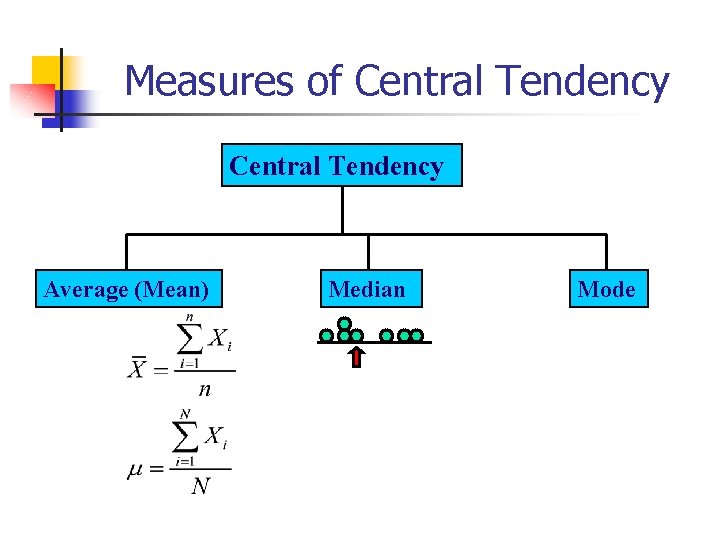
Measures of Central Tendency Average (Mean) Median Mode

Mean (Arithmetic Mean) n Mean (arithmetic mean) of data values n Sample mean Sample Size n Population mean Population Size

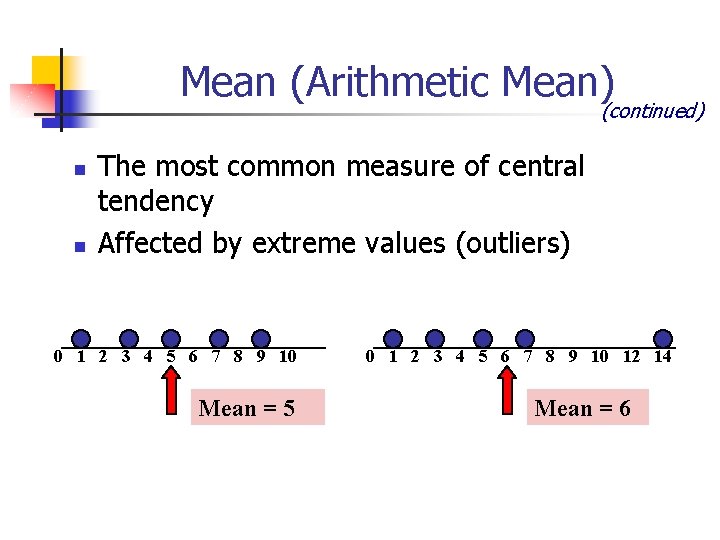
Mean (Arithmetic Mean) (continued) n n The most common measure of central tendency Affected by extreme values (outliers) 0 1 2 3 4 5 6 7 8 9 10 Mean = 5 0 1 2 3 4 5 6 7 8 9 10 12 14 Mean = 6

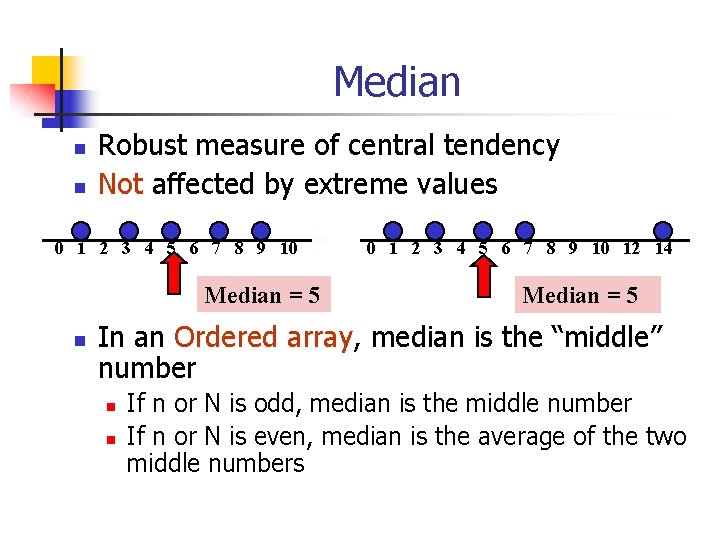
Median n n Robust measure of central tendency Not affected by extreme values 0 1 2 3 4 5 6 7 8 9 10 Median = 5 n 0 1 2 3 4 5 6 7 8 9 10 12 14 Median = 5 In an Ordered array, median is the “middle” number n n If n or N is odd, median is the middle number If n or N is even, median is the average of the two middle numbers

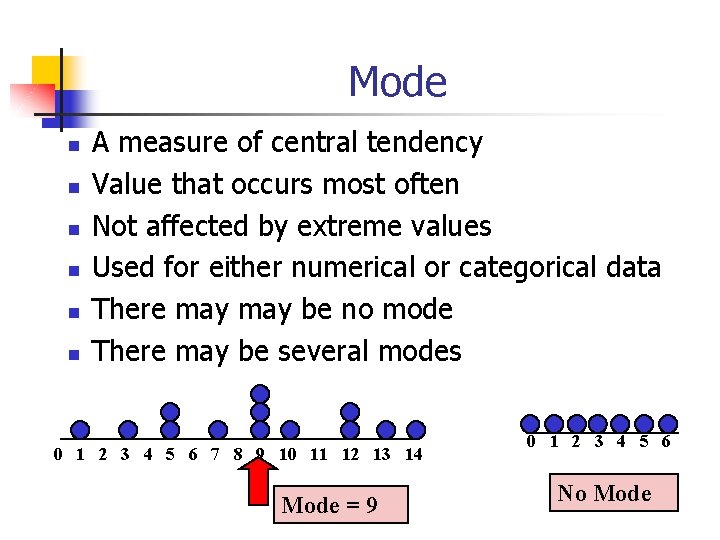
Mode n n n A measure of central tendency Value that occurs most often Not affected by extreme values Used for either numerical or categorical data There may be no mode There may be several modes 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Mode = 9 0 1 2 3 4 5 6 No Mode

Quartiles n Split Ordered Data into 4 Quarters 25% n 25% 25% Position of i-th Quartile Data in Ordered Array: 11 12 13 16 16 17 18 21 22 n n and Are Measures of Noncentral Location = Median, A Measure of Central Tendency

Measures of Variation Variance Standard Deviation Range Interquartile Range Population Variance (σ2) Sample Variance (S 2) Coefficient of Variation Population Standard deviation (σ) Sample Standard deviation (S)

Range n Measure of variation Difference between the largest and the smallest observations: n Ignores the way in which data are distributed n Range = 12 - 7 = 5 7 8 9 10 11 12

Interquartile Range n n Measure of variation Also known as midspread n n Spread in the middle 50% Difference between the first and third quartiles Data in Ordered Array: 11 12 13 16 16 17 n Not affected by extreme values 17 18 21

Variance n n Important measure of variation Shows variation about the mean n Sample variance: n Population variance:

Standard Deviation n Most important measure of variation Shows variation about the mean Has the same units as the original data n Sample standard deviation: n Population standard deviation:

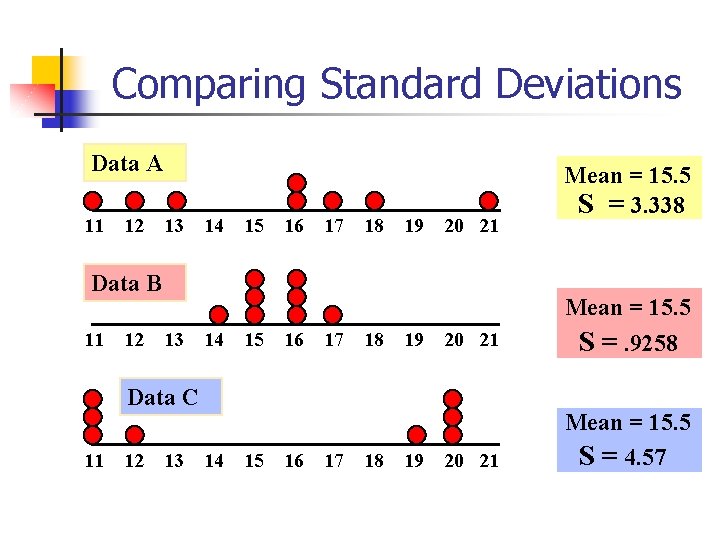
Comparing Standard Deviations Data A 11 12 13 14 15 16 17 18 19 20 21 Data B 11 12 13 14 15 16 17 18 19 20 21 Mean = 15. 5 S =. 9258 20 21 Mean = 15. 5 S = 4. 57 Data C 11 12 13 14 15 16 17 18 19 Mean = 15. 5 S = 3. 338

Coefficient of Variation n Measures relative variation n Always in percentage (%) n Shows variation relative to mean n n Is used to compare two or more sets of data measured in different units

Comparing Coefficient of Variation n Stock A: n n n Stock B: n n n Average price last year = $50 Standard deviation = $5 Average price last year = $100 Standard deviation = $5 Coefficient of variation: n Stock A: n Stock B:

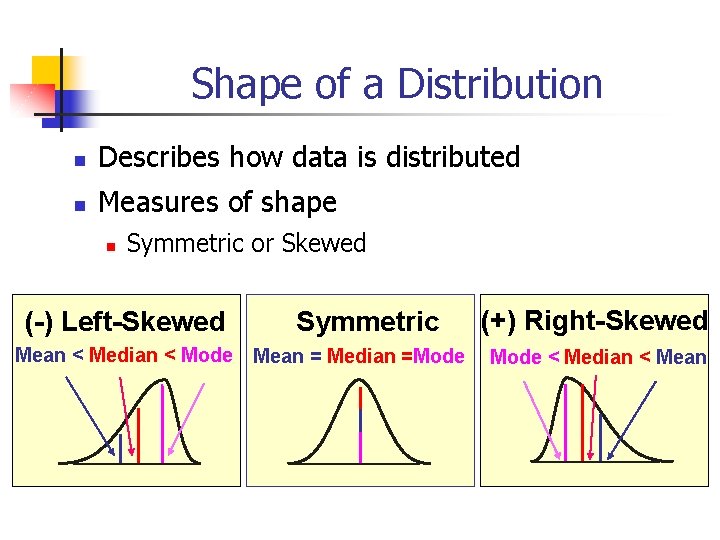
Shape of a Distribution n Describes how data is distributed n Measures of shape n Symmetric or Skewed (-) Left-Skewed Symmetric Mean < Median < Mode Mean = Median =Mode (+) Right-Skewed Mode < Median < Mean

Coefficient of Correlation n Measures the strength of the linear relationship between two quantitative variables

Features of Correlation Coefficient n Unit free n Ranges between – 1 and 1 n n n The closer to – 1, the stronger the negative linear relationship The closer to 1, the stronger the positive linear relationship The closer to 0, the weaker any positive linear relationship

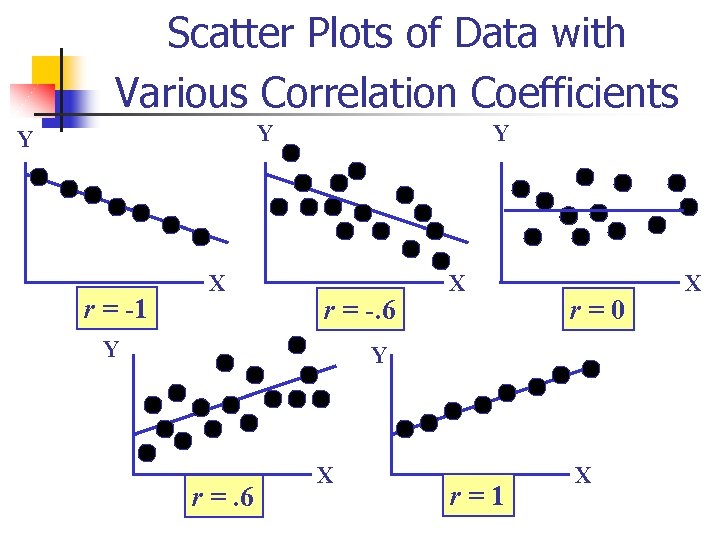
Scatter Plots of Data with Various Correlation Coefficients Y Y r = -1 X Y r = -. 6 Y X r=0 Y r =. 6 X r=1 X X

Chapter Summary n Described measures of central tendency n Mean, median, mode, midrange n Discussed quartile n Described measure of variation n n Illustrated shape of distribution n n Range, interquartile range, variance and standard deviation, coefficient of variation Symmetric, Skewed Discussed correlation coefficient

Stem-n-leaf plot n n n A class took a test. The students' got the following scores. 94 85 77 100 85 95 98 95 First let us draw the stem and leaf plot This makes it easy to see that the mode, the most common score is an 85 since there are three of those scores and all of the other scores have frequencies of either one or tow. It will also make it easier to rank the scores

Stem-n-leaf n This will make it easier to find the median and the quartiles. There as many scores above the median as below. Since there are ten scores, and ten is an even number, we can divide the scores into two equal groups with no scores left over. To find the median, we divide the scores up into the upper five and the lower five.

Box Plot n n n n The five-number summary is an abbreviated way to describe a sample. The five number summary is a list of the following numbers: Minimum First (Lower) Quartile, Median, Third (Upper) Quartile, Maximum The five number summary leads to a graphical representation of a distribution called the boxplot. Boxplots are ideal for comparing two nearly-continuous variables. To draw a boxplot (see the example in the figure below), follow these simple steps: The ends of the box (hinges) are at the quartiles, so that the length of the box is the.

Box plots n n n The median is marked by a line within the box. The two vertical lines (called whiskers) outside the box extend to the smallest and largest observations within of the quartiles. Observations that fall outside of are called extreme outliers and are marked, for example, with an open circle. Observations between and are called mild outliers and are distinguished by a different mark, e. g. , a closed circle.

Example of boxplot n n n The Density of Nitrogen - A Comparison of Two Samples Lord Raleigh was one of the earliest scientists to study the density of nitrogen. In his studies, he noticed something peculiar. The density of nitrogen produced from chemical compounds tended to be smaller than the density of nitrogen produced from the air However, he was working with fairly small samples, and the question is, was he correct in his conjecture? Lord Raleigh's measurements which first appeared in Proceedings, Royal Society (London, 55, 1894 pp. 340 -344) are produced below. The units are the mass of nitrogen filling a certain flask under specified pressure and temperature. 1. Calculate the summary statistics for each set of data. 2. Construct side-by-side box plots.

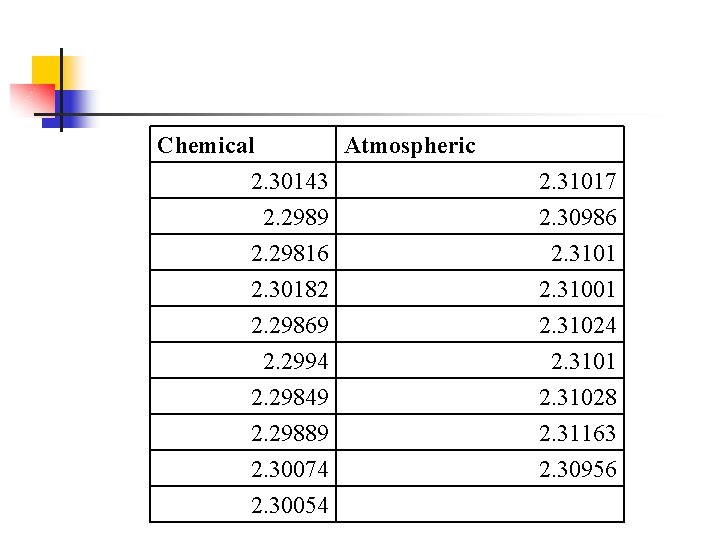
Chemical Atmospheric 2. 30143 2. 2989 2. 29816 2. 30182 2. 29869 2. 2994 2. 29849 2. 29889 2. 30074 2. 30054 2. 31017 2. 30986 2. 3101 2. 31024 2. 3101 2. 31028 2. 31163 2. 30956

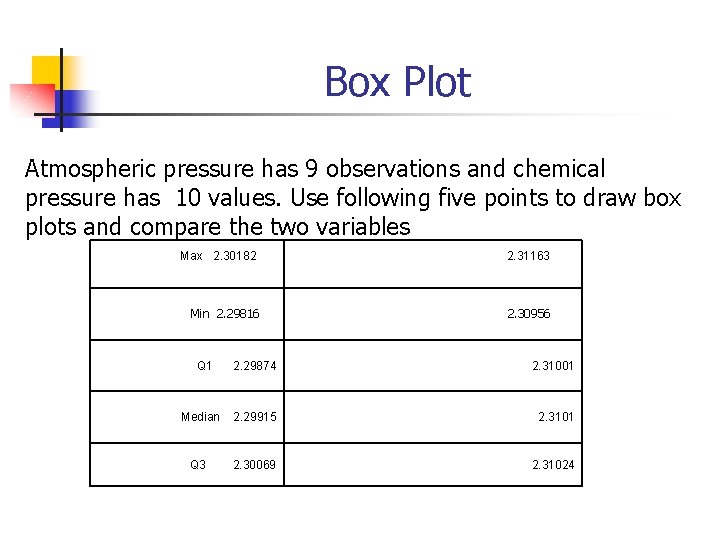
Box Plot Atmospheric pressure has 9 observations and chemical pressure has 10 values. Use following five points to draw box plots and compare the two variables Max 2. 30182 2. 31163 Min 2. 29816 2. 30956 Q 1 2. 29874 2. 31001 Median 2. 29915 2. 3101 Q 3 2. 30069 2. 31024